Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T12:16:13.335Z Has data issue: false hasContentIssue false
  • English
  • Français

Waves in a warm pair plasma: a relativistically complete two-fluid analysis

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  27 August 2019

Rony Keppens Open the ORCID record for Rony Keppens [Opens in a new window] ,
Hans Goedbloed  and
Jean-Baptiste Durrive
Rony Keppens*
Affiliation:
Centre for mathematical Plasma Astrophysics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium School of Astronomy and Space Science, Nanjing University, PR China Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing, PR China
Hans Goedbloed
Affiliation:
DIFFER, TU/e Science Park, 5612AJ Eindhoven, The Netherlands
Jean-Baptiste Durrive
Affiliation:
Research Institute in Astrophysics and Planetology (IRAP), University of Toulouse, Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an ideal two-fluid wave mode analysis for a pair plasma, extending an earlier study for cold conditions to the warm pair plasma case. Starting from the completely symmetrized means for writing the governing linearized equations in the pair fluid rest frame, we discuss the governing dispersion relation containing all six pairs of forward and backward propagating modes, which are conveniently labelled as S, A, F, M, O and X. These relate to the slow (S), Alfvén (A) and fast (F) magnetohydrodynamic waves, include a modified (M) electrostatic mode, as well as the electromagnetic O and X branches. In the dispersion relation, only two parameters appear, which define the pair plasma magnetization 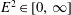$E^{2}\in [0,\infty ]$ and the squared pair plasma sound speed 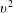$v^{2}$, measured in units of the light speed $c$. The description is valid also in the highly relativistic regime, where either a high magnetization and/or a relativistic temperature (hence sound speed) is reached. We recover the exact relativistic single-fluid magnetohydrodynamic expressions for the S, A and F families in the low wavenumber–frequency regime, which can be obtained for any choice of the equation of state. We argue that, as in a cold pair plasma, purely parallel or purely perpendicular propagation with respect to the magnetic field vector 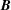$\boldsymbol{B}$ is special, and near-parallel or near-perpendicular orientations demonstrate avoided crossings of branches at computable wavenumbers and frequencies. The complete six-mode phase and group diagram views are provided as well, visually demonstrating the intricate anisotropies in all wave modes, as well as their transformations. Analytic expressions for all six wave group speeds at both small and large wavenumbers complement the analysis.

Keywords

astrophysical plasmascomplex plasmasplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 4 , August 2019 , 905850408
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arons, J. & Barnard, J. J. 1986 Wave propagation in pulsar magnetospheres – dispersion relations and normal modes of plasmas in superstrong magnetic fields. Astrophys. J. 302, 120–137.Google Scholar
Bellan, P. M. 2012 Improved basis set for low frequency plasma waves. J. Geophys. Res. (Space Physics) 117, A12219.Google Scholar
Bittencourt, J. A. 2004 Fundamentals of Plasma Physics. Springer.Google Scholar
Boyd, T. J. M. & Sanderson, J. J. 2003 The Physics of Plasmas. Cambridge University Press.Google Scholar
Bret, A. & Narayan, R. 2018 Density jump as a function of magnetic field strength for parallel collisionless shocks in pair plasmas. J. Plasma Phys. 84 (6), 905840604.Google Scholar
Cally, P. S. 2006 Dispersion relations, rays and ray splitting in magnetohelioseismology. Phil. Trans. R. Soc. Lond. A 364 (1839), 333–349.Google Scholar
Chen, F. F. 2016 Introduction to Plasma Physics and Controlled Fusion. Springer.Google Scholar
Claes, N. & Keppens, R. 2019 Thermal stability of magnetohydrodynamic modes in homogeneous plasmas. Astron. Astrophys. 624, A96.Google Scholar
Clemmow, P. C. & Mullaly, R. F. 1955 The dependence of the refractive index in magneto-ionic theory on the direction of the wave normal. In Physics of the Ionosphere, Rep. Phys. Soc. Conf., Cavendish Laboratory, p. 340. London Physical Society.Google Scholar
Damiano, P. A., Wright, A. N. & McKenzie, J. F. 2009 Properties of Hall magnetohydrodynamic waves modified by electron inertia and finite Larmor radius effects. Phys. Plasmas 16 (6), 062901.Google Scholar
Denisse, J. F. & Delcroix, J. L. 1961 Théorie des ondes dans les plasmas. Dunod. (Transl.: Plasma Waves, 1963, John Wiley).Google Scholar
Goedbloed, J. P., Keppens, R. & Poedts, S. 2010 Advanced Magnetohydrodynamics. Cambridge University Press.Google Scholar
Goedbloed, J. P., Keppens, R. & Poedts, S. 2019 Magnetohydrodynamics of Laboratory and Astrophysical Plasmas. Cambridge University Press.Google Scholar
Goedbloed, J. P. & Poedts, S. 2004 Principles of Magnetohydrodynamics. Cambridge University Press.Google Scholar
Gurnett, D. A. & Bhattacharjee, A. 2005 Introduction to Plasma Physics. Cambridge University Press.Google Scholar
Ishida, A., Cheng, C. Z. & Peng, Y.-K. M. 2005 Properties of low and medium frequency modes in two-fluid plasma. Phys. Plasmas 12 (5), 052113.Google Scholar
Keppens, R. & Goedbloed, H. 2019a A fresh look at waves in ion–electron plasmas. Front. Astron. Space Sci. 6, 11.Google Scholar
Keppens, R. & Goedbloed, H. 2019b Wave modes in a cold pair plasma: the complete phase and group diagram point of view. J. Plasma Phys. 85 (1), 175850101.Google Scholar
Keppens, R. & Meliani, Z. 2008 Linear wave propagation in relativistic magnetohydrodynamics. Phys. Plasmas 15 (10), 102103.Google Scholar
Kulsrud, R. M. 2005 Plasma Physics for Astrophysics, Princeton Series in Astrophysics. Princeton University Press.Google Scholar
Loureiro, N. F. & Boldyrev, S. 2018 Turbulence in magnetized pair plasmas. Astrophys. J. Lett. 866, L14.Google Scholar
Lyutikov, M. 1998 Waves in a one-dimensional magnetized relativistic pair plasma. Mon. Not. R. Astron. Soc. 293 (4), 447–468.Google Scholar
Lyutikov, M. 1999 Beam instabilities in a magnetized pair plasma. J. Plasma Phys. 62, 65–86.Google Scholar
Mathews, W. G. 1971 The hydromagnetic free expansion of a relativistic gas. Astrophys. J. 165, 147.Google Scholar
Mignone, A., Mattia, G. & Bodo, G. 2018 Linear wave propagation for resistive relativistic magnetohydrodynamics. Phys. Plasmas 25 (9), 092114.Google Scholar
Rafat, M. Z., Melrose, D. B. & Mastrano, A. 2019 Wave dispersion in pulsar plasma. Part 1. Plasma rest frame. J. Plasma Phys. 85, 905850305.Google Scholar
Sarri, G., Poder, K., Cole, J. M., Schumaker, W., di Piazza, A., Reville, B., Dzelzainis, T., Doria, D., Gizzi, L. A., Grittani, G. et al. 2015 Generation of neutral and high-density electron–positron pair plasmas in the laboratory. Nat. Commun. 6, 6747.Google Scholar
Stewart, G. A. & Laing, E. W. 1992 Wave propagation in equal-mass plasmas. J. Plasma Phys. 47, 295–319.Google Scholar
Stix, T. H. 1992 Waves in Plasmas. American Institute of Physics.Google Scholar
Stringer, T. E. 1963 Low-frequency waves in an unbounded plasma. J. Nucl. Energy 5, 89–107.Google Scholar
Synge, J. L. 1960 Relativity: The General Theory. North Holland.Google Scholar
Thorne, K. S. & Blandford, R. D. 2017 Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics. Princeton University Press.Google Scholar
Zenitani, S. 2018 Dissipation in relativistic pair-plasma reconnection: revisited. Plasma Phys. Control. Fusion 60 (1), 014028.Google Scholar
Zhao, J. 2015 Dispersion relations and polarizations of low-frequency waves in two-fluid plasmas. Phys. Plasmas 22 (4), 042115.Google Scholar
Zhao, J. 2017 Properties of Whistler waves in warm electron plasmas. Astrophys. J. 850, 13.Google Scholar