Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T03:46:08.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave dispersion in pulsar plasma. Part 3. Beam-driven instabilities

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  05 November 2019

M. Z. Rafat Open the ORCID record for M. Z. Rafat [Opens in a new window] ,
D. B. Melrose Open the ORCID record for D. B. Melrose [Opens in a new window]  and
A. Mastrano Open the ORCID record for A. Mastrano [Opens in a new window]
M. Z. Rafat
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
D. B. Melrose*
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
A. Mastrano
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Beam-driven instabilities are considered in a pulsar plasma assuming that both the background plasma and the beam are relativistic Jüttner distributions. In the rest frame of the background, the only waves that can satisfy the resonance condition are in a tiny range of slightly subluminal phase speeds. The growth rate for the kinetic (or maser) version of the weak-beam instability is much smaller than has been estimated for a relativistically streaming Gaussian distribution, and the reasons for this are discussed. The growth rate for the reactive version of the weak-beam instability is treated in a conventional way. We compare the results with exact calculations, and find that the approximate solutions are not consistent with the exact results. We conclude that, for plausible parameters, there is no reactive version of the instability. The growth rate in the pulsar frame is smaller than that in the rest frame of the background plasma by a factor 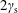$2\unicode[STIX]{x1D6FE}_{\text{s}}$, where 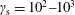$\unicode[STIX]{x1D6FE}_{\text{s}}=10^{2}{-}10^{3}$ is the Lorentz factor of the bulk motion of the background plasma, placing a further constraint on effective wave growth. Based on these results, we argue that beam-driven wave growth probably plays no role in pulsar radio emission.

Keywords

astrophysical plasmasplasma instabilitiesplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 6 , December 2019 , 905850603
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, P. N. Jr & Eilek, J. A. 2002 Pair creation in the pulsar magnetosphere. Astrophys. J. 581, 451–469.Google Scholar
Asseo, E. 1993 Microtexture in the pulsar radio emission zone. Mon. Not. R. Astron. Soc. 264, 940.Google Scholar
Asseo, E. 1995 The importance of boundary effects in the emission region of the pulsar magnetosphere. Mon. Not. R. Astron. Soc. 276, 74–102.Google Scholar
Asseo, E. & Melikidze, G. I. 1998 Non-stationary pair plasma in a pulsar magnetosphere and the two-stream instability. Mon. Not. R. Astron. Soc. 301, 59–71.Google Scholar
Asseo, E., Pellat, R. & Sol, H. 1983 Radiative or two-stream instability as a source for pulsar radio emission. Astrophys. J. 266, 201–214.Google Scholar
Asseo, E. & Riazuelo, A. 2000 Relativistic anisotropic pair plasmas. Mon. Not. R. Astron. Soc. 318, 983–1004.Google Scholar
Benford, G. & Buschauer, R. 1977 Coherent pulsar radio radiation by antenna mechanisms – general theory. Mon. Not. R. Astron. Soc. 179, 189–207.Google Scholar
Egorenkov, V. D., Lominadze, D. G. & Mamradze, P. G. 1983 Beam instability of the plasma in pulsar magnetospheres. Astrophysics 19, 426–431.Google Scholar
Eilek, J. A. & Hankins, T. H. 2016 Radio emission physics in the Crab pulsar. J. Plasma Phys. 82 (3), 635820302.Google Scholar
Gedalin, M., Gruman, E. & Melrose, D. B. 2002a Mechanism of pulsar radio emission. Mon. Not. R. Astron. Soc. 337, 422–430.Google Scholar
Gedalin, M., Gruman, E. & Melrose, D. B. 2002b New mechanism of pulsar radio emission. Phys. Rev. Lett. 88 (12), 121101.Google Scholar
Hardee, P. E. & Rose, W. K. 1976 A mechanism for the production of pulsar radio radiation. Astrophys. J. 210, 533–538.Google Scholar
Hardee, P. E. & Rose, W. K. 1978 Wave production in an ultrarelativistic electron–positron plasma. Astrophys. J. 219, 274–287.Google Scholar
Hinata, S. 1976a Level of electrostatic excitation associated with relativistic beam-plasma system and pulsar radiation. Astrophys. Space Sci. 44, 389–395.Google Scholar
Hinata, S. 1976b Relativistic plasma turbulence and its application to pulsar phenomena. Astrophys. J. 206, 282–294.Google Scholar
Jüttner, F. 1911 Das Maxwellsche Gesetz der Geschwindigkeitsverteilung in der Relativtheorie. Ann. Phys. 339, 856–882.Google Scholar
Lominadze, D. G. & Mikhailovskiǐ, A. B. 1979 Longitudinal waves and two-stream instability in a relativistic plasma. Sov. Phys. JETP 49, 483.Google Scholar
Lominadze, D. G., Mikhaǐlovskiǐ, A. B. & Sagdeev, R. Z. 1979 Langmuir turbulence of a relativistic plasma in a strong magnetic field. Sov. Phys. JETP 50, 927.Google Scholar
Lominadze, J. G. & Pataraya, A. D. 1982 Some nonlinear mechanisms of pulsar emission. Phys. Scr. T2, 215–222.Google Scholar
Lominadze, J. G., Stenflo, L., Tsytovich, V. N. & Wilhelmsson, H. 1982 A new explanation of the high effective temperatures in pulsar radioemissions. Physica Scripta 26, 455–458.Google Scholar
Lyubarskii, Y. E. 1992 Possible mechanism of pulsar radio emission. Astron. Astrophys. 265, L33–L36.Google Scholar
Lyubarskii, Y. E. 1996 Generation of pulsar radio emission. Astron. Astrophys. 308, 809–820.Google Scholar
Lyutikov, M. 2000 Excitation of Alfvén waves and pulsar radio emission. Mon. Not. R. Astron. Soc. 315, 31–36.Google Scholar
Magneville, A. 1990 Plasma waves in hot relativistic beam-plasma systems. Part 1. Dispersion relations. J. Plasma Phys. 44 (2), 191–211.Google Scholar
Magneville, A. 1990 Plasma waves in hot relativistic beam-plasma systems. Part 2. Kinetic and hydrodynamic instabilities. J. Plasma Phys. 44 (2), 213–229.Google Scholar
Melikidze, G. I., Gil, J. A. & Pataraya, A. D. 2000 The spark-associated soliton model for pulsar radio emission. Astrophys. J. 544, 1081–1096.Google Scholar
Melrose, D. B. 1986 Instabilities in Space and Laboratory Plasmas. Cambridge University Press.Google Scholar
Melrose, D. B. & Gedalin, M. E. 1999 Relativistic plasma emission and pulsar radio emission: a critique. Astrophys. J. 521, 351–361.Google Scholar
Mitra, D., Gil, J. & Melikidze, G. I. 2009 Unraveling the nature of coherent pulsar radio emission. Astrophys. J. Lett. 696, L141–L145.Google Scholar
Rafat, M. Z., Melrose, D. B. & Mastrano, A. 2019a Wave dispersion in pulsar plasma. Part 1. Plasma rest frame. J. Plasma Phys. 85 (3), 905850305.Google Scholar
Rafat, M. Z., Melrose, D. B. & Mastrano, A. 2019b Wave dispersion in pulsar plasma. Part 2. Pulsar frame. J. Plasma Phys. 85 (3), 905850311.Google Scholar
Suvorov, E. V. & Chugunov, Y. V. 1973 Distribution function of relativistic electrons in a strong magnetic field. Astrophys. Space Sci. 23, 189–199.Google Scholar
Suvorov, E. V. & Chugunov, Y. V. 1975 Electromagnetic waves in a relativistic plasma with a strong magnetic field. Astrophysics 11, 203–222.Google Scholar
Synge, J. L. 1957 The Relativistic Gas. North-Holland.Google Scholar
Tsytovich, V. N. & Kaplan, S. A. 1972 Relativistic turbulent plasma in pulsars. Astrofizika 8, 441–460.Google Scholar
Ursov, V. N. & Usov, V. V. 1988 Plasma flow nonstationarity in pulsar magnetospheres and two-stream instability. Astrophys. Space Sci. 140, 325–336.Google Scholar
Usov, V. V. 1987 On two-stream instability in pulsar magnetospheres. Astrophys. J. 320, 333–335.Google Scholar
Weatherall, J. C. 1994 Streaming instability in relativistically hot pulsar magnetospheres. Astrophys. J. 428, 261–266.Google Scholar
Wright, T. P. & Hadley, G. R. 1975 Relativistic distribution functions and applications to electron beams. Phys. Rev. A 12, 686–697.Google Scholar