Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T02:13:42.732Z Has data issue: false hasContentIssue false
  • English
  • Français

Vacuum magnetic fields with exact quasisymmetry near a flux surface. Part 1. Solutions near an axisymmetric surface

Part of: Focus on Fusion

Published online by Cambridge University Press:  09 March 2021

Wrick Sengupta Open the ORCID record for Wrick Sengupta [Opens in a new window] ,
Elizabeth J. Paul Open the ORCID record for Elizabeth J. Paul [Opens in a new window] ,
Harold Weitzner Open the ORCID record for Harold Weitzner [Opens in a new window]  and
Amitava Bhattacharjee Open the ORCID record for Amitava Bhattacharjee [Opens in a new window]
Wrick Sengupta*
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY10012, USA
Elizabeth J. Paul
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ08543, USA
Harold Weitzner
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY10012, USA
Amitava Bhattacharjee
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ08543, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

While several results have pointed to the existence of exactly quasisymmetric fields on a surface (Garren & Boozer, Phys. Fluids B, vol. 3, 1991, pp. 2805–2821; 2822–2834; Plunk & Helander, J. Plasma Phys., vol. 84, 2018, 905840205), we have obtained the first such solutions using a vacuum surface expansion formalism. We obtain a single nonlinear parabolic partial differential equation for a function 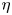$\eta$ such the field strength satisfies 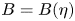$B = B(\eta )$. Closed-form solutions are obtained in cylindrical, slab and isodynamic geometries. Numerical solutions of the full nonlinear equations in general axisymmetric toroidal geometry are obtained, resulting in a class of quasihelical local vacuum equilibria near an axisymmetric surface. The analytic models provide additional insight into general features of the nonlinear solutions, such as localization of the surface perturbations on the inboard side. The local solutions thus obtained can be continued globally only for special initial surfaces.

Keywords

fusion plasmaplasma devicesplasma confinement
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 2 , April 2021 , 905870205
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bers, L. 1953 Theory of Pseudo-analytic Functions. New York University. Institute for Mathematics and Mechanics.Google Scholar
Boozer, A. H. 1983 Transport and isomorphic equilibria. Phys. Fluids 26 (2), 496.CrossRefGoogle Scholar
Boozer, A. H. 2002 Local equilibrium of nonrotating plasmas. Phys. Plasmas 9 (9), 3762–3766.CrossRefGoogle Scholar
Boozer, A. H. 2019 Curl-free magnetic fields for stellarator optimization. Phys. Plasmas 26 (10), 102504.CrossRefGoogle Scholar
Boozer, A. H. 2020 Why carbon dioxide makes stellarators so important. Nucl. Fusion 60 (6), 065001.CrossRefGoogle Scholar
Burby, J. W., Kallinikos, N. & MacKay, R. S. 2020 Some mathematics for quasi-symmetry. J. Math. Phys. 61 (9), 093503.CrossRefGoogle Scholar
Candy, J. & Belli, E. A. 2015 Non-axisymmetric local magnetostatic equilibrium. J. Plasma Phys. 81 (3).CrossRefGoogle Scholar
Constantin, P., Drivas, T. D. & Ginsberg, D. 2021 On quasisymmetric plasma equilibria sustained by small force. J. Plasma Phys. 87 (1), 905870111.CrossRefGoogle Scholar
Drevlak, M., Beidler, C. D., Geiger, J., Helander, P. & Turkin, Y. 2018 Optimisation of stellarator equilibria with ROSE. Nucl. Fusion 59 (1), 016010.CrossRefGoogle Scholar
Elbarmi, E., Sengupta, W. & Weitzner, H. 2020 Charged particle dynamics near an X-point of a non-symmetric magnetic field with closed field lines. J. Plasma Phys. 86 (2), 905860209.CrossRefGoogle Scholar
Garren, D. A. & Boozer, A. H. 1991 a Existence of quasihelically symmetric stellarators. Phys. Fluids B 3 (10), 2822–2834.CrossRefGoogle Scholar
Garren, D. A. & Boozer, A. H. 1991 b Magnetic field strength of toroidal plasma equilibria. Phys. Fluids B 3 (10), 2805–2821.CrossRefGoogle Scholar
Hegna, C. C. 2000 Local three-dimensional magnetostatic equilibria. Phys. Plasmas 7 (10), 3921– 3928.CrossRefGoogle Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.CrossRefGoogle ScholarPubMed
Helander, P. & Simakov, A. N. 2008 Intrinsic ambipolarity and rotation in stellarators. Phys. Rev. Lett. 101 (14), 145003.CrossRefGoogle ScholarPubMed
Henneberg, S. A., Drevlak, M. & Helander, P. 2019 Improving fast-particle confinement in quasi-axisymmetric stellarator optimization. Plasma Phys. Control. Fusion 62 (1), 014023.CrossRefGoogle Scholar
Hirshman, S. P. & Whitson, J. C. 1983 Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553–3568.CrossRefGoogle Scholar
Imbert-Gerard, L.-M., Paul, E. & Wright, A. 2019 An introduction to symmetries in stellarators. arXiv:1908.05360.Google Scholar
Jaquiery, E. & Sengupta, W. 2019 Low-shear three-dimensional equilibria in a periodic cylinder. J. Plasma Phys. 85 (1), 905850115.CrossRefGoogle Scholar
Jorge, R. & Landreman, M. 2021 The use of near-axis magnetic fields for stellarator turbulence simulations. Plasma Phys. Control. Fusion 63, 014001.CrossRefGoogle Scholar
Jorge, R., Sengupta, W. & Landreman, M. 2020 a Construction of quasisymmetric stellarators using a direct coordinate approach. Nucl. Fusion 60, 076021.CrossRefGoogle Scholar
Jorge, R., Sengupta, W. & Landreman, M. 2020 b Near-axis expansion of stellarator equilibrium at arbitrary order in the distance to the axis. J. Plasma Phys. 86 (1), 905860106.CrossRefGoogle Scholar
Landreman, M. 2019 a Optimized quasisymmetric stellarators are consistent with the Garren–Boozer construction. Plasma Phys. Control. Fusion 61 (7), 075001.CrossRefGoogle Scholar
Landreman, M. 2019 b Quasisymmetry: a hidden symmetry of magnetic fields. https://terpconnect.umd.edu/mattland/assets/notes/Introduction_to_quasisym.Google Scholar
Landreman, M. & Catto, P. J. 2012 Omnigenity as generalized quasisymmetry. Phys. Plasmas 19 (5), 056103.CrossRefGoogle Scholar
Landreman, M. & Jorge, R. 2020 Magnetic well and mercier stability of stellarators near the magnetic axis. J. Plasma Phys. 86 (5), 905860510.CrossRefGoogle Scholar
Landreman, M. & Sengupta, W. 2018 Direct construction of optimized stellarator shapes. Part 1. Theory in cylindrical coordinates. J. Plasma Phys. 84 (6).CrossRefGoogle Scholar
Landreman, M. & Sengupta, W. 2019 Constructing stellarators with quasisymmetry to high order. J. Plasma Phys. 85 (6).CrossRefGoogle Scholar
Landreman, M., Sengupta, W. & Plunk, G. G. 2019 Direct construction of optimized stellarator shapes. Part 2. Numerical quasisymmetric solutions. J. Plasma Phys. 85 (1).CrossRefGoogle Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129, 113.CrossRefGoogle Scholar
Palumbo, D. 1968 Some considerations on closed configurations of magnetohydrostatic equilibrium. Il Nuovo Cimento B 53 (2), 507–511.CrossRefGoogle Scholar
Plunk, G. G. 2020 Perturbing an axisymmetric magnetic equilibrium to obtain a quasi-axisymmetric stellarator. J. Plasma Phys. 86 (4), 905860409.CrossRefGoogle Scholar
Plunk, G. G. & Helander, P. 2018 Quasi-axisymmetric magnetic fields: weakly non-axisymmetric case in a vacuum. J. Plasma Phys. 84 (2).CrossRefGoogle Scholar
Rodriguez, E. & Bhattacharjee, A. 2021 a Solving the problem of overdetermination of quasisymmetric equilbrium solutions by near-axis expansions. I. Generalised force balance. Phys. Plasmas 28 (1), 012508.CrossRefGoogle Scholar
Rodriguez, E. & Bhattacharjee, A. 2021 b Solving the problem of overdetermination of quasisymmetric equilibrium solutions by near-axis expansions. II. Circular axis stellarator solutions. Phys. Plasmas 28 (1), 012509.CrossRefGoogle Scholar
Rodriguez, E., Helander, P. & Bhattacharjee, A. 2020 Necessary and sufficient conditions for quasisymmetry. Phys. Plasmas 27 (6), 062501.CrossRefGoogle Scholar
Sanchez, R., Hirshman, S. P., Ware, A. S., Berry, L. A. & Spong, D. A. 2000 Ballooning stability optimization of low-aspect-ratio stellarators. Plasma Phys. Control. Fusion 42 (6), 641.CrossRefGoogle Scholar
Sengupta, W. & Weitzner, H. 2019 Low-shear three-dimensional equilibria and vacuum magnetic fields with flux surfaces. J. Plasma Phys. 85 (2), 905850209.CrossRefGoogle Scholar
Skovoroda, A. A. 2009 Local surface equilibrium equations for currentless magnetic configurations. Plasma Phys. Rep. 35 (2), 99–111.CrossRefGoogle Scholar
Spong, D. A., Hirshman, S. P., Berry, L. A., Lyon, J. F., Fowler, R. H., Strickler, D. J., Cole, M. J., Nelson, B. N., Williamson, D. E., Ware, A. S., et al. 2001 Physics issues of compact drift optimized stellarators. Nucl. Fusion 41 (6), 711.CrossRefGoogle Scholar
Weitzner, H. 2016 Expansions of non-symmetric toroidal magnetohydrodynamic equilibria. Phys. Plasmas 23 (6), 062512.CrossRefGoogle Scholar
Weitzner, H. & Sengupta, W. 2020 Exact non-symmetric closed line vacuum magnetic fields in a topological torus. Phys. Plasmas 27 (2), 022509.CrossRefGoogle Scholar