Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T10:15:45.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional surface waves in magnetohydrodynamics

Published online by Cambridge University Press:  15 July 2019

Matthew Hunt Open the ORCID record for Matthew Hunt [Opens in a new window]
Matthew Hunt*
Affiliation:
Warwick Manufacturing Group, University of Warwick, Coventry CV4 7AL, UK Warwick Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The study of nonlinear waves in water has a long history beginning with the seminal paper by Korteweg & de Vries (Phil. Mag., vol. 39, 1895, p. 240) and more recently for magnetohydrodynamics Danov & Ruderman (Fluid Dyn., vol. 18, 1983, pp. 751–756). The appearance of a Hilbert transform in the nonlinear equation for magnetohydrodynamics (MHD) distinguishes it from the water wave model description. In this paper, we are interested in examining weakly nonlinear interfacial waves in 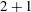$2+1$ dimensions. First, we determine the wave solution in the linear case. Next, we derive the corresponding generalisation for the Kadomtsev–Petviashvili (KP) equation with the inclusion of an equilibrium magnetic field. The derived governing equation is a generalisation of the Benjamin–Ono (BO) equation called the Benjamin equation first derived in Benjamin (J. Fluid Mech., vol. 245, 1992, pp. 401–411) and in the higher-dimensional context in Kim & Akylas (J. Fluid Mech., vol. 557, 2006, pp. 237–256).

Keywords

plasma wavesastrophysical plasmasplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 4 , August 2019 , 905850405
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barcilon, A. & Fitzjerald, D. 1985 A nonlinear steady model for moist hydrstatic mountain waves. J. Atmos. Sci. 42 (1).Google Scholar
Benjamin, T. B. 1967 Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 29, 559–562.Google Scholar
Benjamin, T. B. 1992 A new kind of solitary wave. J. Fluid Mech. 245, 401–411.Google Scholar
Danov, K. D. & Ruderman, M. S. 1983 Nonlinear waves on shallow water in the presence of a horizontal magnetic field. Fluid Dyn. 18, 751–756.Google Scholar
Edwin, P. M. & Roberts, B. 1986 The Benjamin–Ono equation: an application in solar physics. Wave Motion 8, 151–158.Google Scholar
Gerbeau, J.-F., Bris, C. L. & Lelièvre, T. 2006 Mathematical Methods for the Magnetohydrodynamics of Liquid Metals. Oxford University Press.Google Scholar
Hunt, M. J.2013 Linear and nonlinear free surface flows in electrohydrodynamics. PhD thesis, University College London.Google Scholar
Hunt, M. J., Vanden-Broeck, J.-M., Papageorgiou, P. D. & Parau, E. I. 2017 Benjamin–Ono Kadomtsev–Petviashvili’s models in interfacial electro-hydrodynamics. Eur. J. Mech. (B/Fluids) 65.Google Scholar
Johnson, R. S. 1997 A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge University Press.Google Scholar
Kim, B. & Akylas, T. R. 2006 On gravity-capillary lumps. Part 2. Two dimensional benjamin equation. J. Fluid Mech. 557, 237–256.Google Scholar
Korteweg, D. J. & de Vries, G. 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. 39, 240.Google Scholar
Melcher, J. R. 1963 Field Coupled Surface Waves. MIT Press.Google Scholar
Ono, H. 1975 Algebraic solitary waves in stratified fluids. J. Phys. Soc. Japan 39, 1082–1091.Google Scholar
Roberts, B. 1985 Solitary waves in a magnetic flux tube. Phys. Fluids 28, 3280.Google Scholar
Zaiter, I. 2009 Solitary waves of the two-dimensional benjamin equation. Adv. Differ. Equ. 14, 835–874.Google Scholar