Article contents
Theory of the tertiary instability and the Dimits shift within a scalar model
Published online by Cambridge University Press: 20 August 2020
Abstract
The Dimits shift is the shift between the threshold of the drift-wave primary instability and the actual onset of turbulent transport in a magnetized plasma. It is generally attributed to the suppression of turbulence by zonal flows, but developing a more detailed understanding calls for consideration of specific reduced models. The modified Terry–Horton system has been proposed by St-Onge (J. Plasma Phys., vol. 83, 2017, 905830504) as a minimal model capturing the Dimits shift. Here, we use this model to develop an analytic theory of the Dimits shift and a related theory of the tertiary instability of zonal flows. We show that tertiary modes are localized near extrema of the zonal velocity 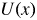 $U(x)$, where
$U(x)$, where 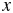 $x$ is the radial coordinate. By approximating
$x$ is the radial coordinate. By approximating 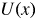 $U(x)$ with a parabola, we derive the tertiary-instability growth rate using two different methods and show that the tertiary instability is essentially the primary drift-wave instability modified by the local
$U(x)$ with a parabola, we derive the tertiary-instability growth rate using two different methods and show that the tertiary instability is essentially the primary drift-wave instability modified by the local 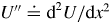 $U'' \doteq {\rm d}^2 U/{\rm d} x^2 $. Then, depending on
$U'' \doteq {\rm d}^2 U/{\rm d} x^2 $. Then, depending on 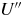 $U''$, the tertiary instability can be suppressed or unleashed. The former corresponds to the case when zonal flows are strong enough to suppress turbulence (Dimits regime), while the latter corresponds to the case when zonal flows are unstable and turbulence develops. This understanding is different from the traditional paradigm that turbulence is controlled by the flow shear
$U''$, the tertiary instability can be suppressed or unleashed. The former corresponds to the case when zonal flows are strong enough to suppress turbulence (Dimits regime), while the latter corresponds to the case when zonal flows are unstable and turbulence develops. This understanding is different from the traditional paradigm that turbulence is controlled by the flow shear 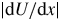 $| {\rm d} U / {\rm d} x |$. Our analytic predictions are in agreement with direct numerical simulations of the modified Terry–Horton system.
$| {\rm d} U / {\rm d} x |$. Our analytic predictions are in agreement with direct numerical simulations of the modified Terry–Horton system.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by


