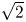1. Introduction
The mechanisms by which high-energy cosmic rays are accelerated is an unresolved issue which attracts considerable attention. Fermi proposed that the interaction between particles and magnetic fields in the cosmic environment was responsible for the inverse power law spectra of the cosmic radiation (Fermi Reference Fermi1949): this is known as Fermi acceleration. Fermi acceleration is expected in collisionless shocks found in extreme astrophysical environments (Sagdeev Reference Sagdeev1966; Tidman Reference Tidman1969) which grow from Weibel instabilities (Weibel Reference Weibel1959). In the astrophysical context, the only way to probe these acceleration mechanisms is from telescopic observation of their radiation spectra. With the development of high-power lasers (Maine et al. Reference Maine, Strickland, Bado, Pessot and Mourou1988) and advanced diagnostic techniques, a new field of laboratory astrophysics has been opened up (Remington et al. Reference Remington, Arnett, Paul and Takabe1999). This allows for aspects of these astrophysical environments to be mimicked in a laboratory setting where the plasmas can be probed directly with diagnostics and compared with numerical simulations (Dawson Reference Dawson1983). For example, the interaction between intense relativistic laser light with solid targets can accelerate ions to high energies under various mechanisms (Passoni, Bertagna & Zani Reference Passoni, Bertagna and Zani2010), including shock formation (He et al. Reference He, Dong, Sheng, Weng, Chen, Wu and Zhang2007). Furthermore, direct observation of turbulent magnetic fields in hot dense laser target interactions has been reported (Mondal et al. Reference Mondal, Narayanan, Ding, Lad, Hao, Ahmad, Wang, Sheng, Sengupta and Kaw2012). The dynamics of plasma beams have been explored experimentally and with simulations (Hsu et al. Reference Hsu, Moser, Merritt, Adams, Dunn, Brockington, Case, Gilmore, Lynn and Messer2015; Liu et al. Reference Liu, Kuramitsu, Moritaka and Chen2017). The interaction between colliding plasma beams shows magnetic compression and experimental evidence of proton acceleration (Higginson et al. Reference Higginson, Korneev, Ruyer, Riquier, Moreno, Béard, Chen, Grassi, Grech and Gremillet2019).
Furthermore, the collision of relativistic beams with plasma mimicking the background interstellar medium near young stellar objects and Herbig–Haro objects has been investigated (Gregory et al. Reference Gregory, Howe, Loupias, Myers, Notley, Sakawa, Oya, Kodama, Koenig and Woolsey2008; Valenzuela et al. Reference Valenzuela, Collins IV, Zick, Narkis, Krasheninnikov and Beg2015). Lepton beams into background electron–proton plasmas are a promising source of high-energy cosmic rays via Weibel-induced moving magnetic islands (Cui et al. Reference Cui, Sheng, Lu, Li and Zhang2015) and can show preferential positron acceleration (Dieckmann et al. Reference Dieckmann, Spencer, Falk and Rowlands2020). The interaction of relativistic plasmas, electron–proton or leptonic, with background plasma are of great importance in the study of these extreme astrophysical environments. Understanding the theoretical dispersion relations of the Weibel instability in these plasmas is crucial.
There has been extensive work in the field of plasma instabilities. Counterstreaming electron–positron pair two beam plasmas have shown an instability, both Weibel and two-stream, depending on beam parameters (Bret et al. Reference Bret, Stockem, Fiuza, Ruyer, Gremillet, Narayan and Silva2013). Detailed three-dimensional (3D) particle-in-cell (PIC) simulations have been performed for interpenetrating electron–positron shells (Fonseca et al. Reference Fonseca, Silva, Tonge, Mori and Dawson2003; Silva et al. Reference Silva, Fonseca, Tonge, Dawson, Mori and Medvedev2003). However, there was no inclusion of a background electron–proton plasma in these models and simulations. Theoretical work using distribution functions and kinetic theory have been performed on relativistic unmagnetised plasmas (Yoon & Davidson Reference Yoon and Davidson1987; Achterberg & Wiersma Reference Achterberg and Wiersma2007; Achterberg, Wiersma & Norman Reference Achterberg, Wiersma and Norman2007; Yoon Reference Yoon2007) which currently are limited to the simplest cases. Further work is needed in the cold-fluid formalism to explore the instabilities in background electron–proton plasmas with beam electron–proton plasma flows and beam lepton pair plasmas (Bret, Gremillet & Dieckmann Reference Bret, Gremillet and Dieckmann2010).
This paper investigates the Weibel instability in three scenarios: counterstreaming electron beams in background plasma, an electron–positron (lepton) beam in background plasma and an electron–proton (plasma) beam in background plasma where all plasmas are cold. The corresponding dispersion relations are derived theoretically in the cold-fluid formalism and compared with fully relativistic two-dimensional (2D) PIC simulations. The theoretical dispersion relation for the Weibel instability is first reviewed following the work in Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996). This dispersion relation is extended to the scenario of three electron populations in which one cold population is at rest with respect to the proton frame at the beginning. It is then further extended to the scenario of a lepton beam incident on a background electron–proton plasma. The lepton beam extension is adapted to the third scenario of a plasma beam incident on a background electron–proton plasma. The relation of the Weibel instability growth rate to the number densities of the plasma species and the beam energies is explored for all cases and compared to PIC simulations. The maximum Weibel instability growth rates are predicted for a range of beam energies and plasma species densities using the newly derived dispersion relations.
2. Theoretical model
2.1. General dispersion relation
The generalised dispersion relation of the plasma instabilities in counterpropagating beams in plasma with a general perturbation wavevector is derived in Califano, Pegoraro & Bulanov (Reference Califano, Pegoraro and Bulanov1997). The transverse mode of the perturbation represents the Weibel instability. However, it is noted that in highly relativistic beams and asymmetric beams the fastest-growing mode may not be the Weibel instability but the scope of this work is determining the growth rates of transverse magnetic fields, potentially leading to Fermi acceleration. Consequently, the reduced transverse dispersion relation for the Weibel instability for an electron–ion plasma is examined following the work by Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996) which is easier to deal with analytically.
An initially uniform plasma contains two counterpropagating electron beams with an immobile neutralising ion background. The electron beams propagate along the $x$![]() -axis of the system and have initial unperturbed number densities defined as $n_{0\alpha }$
-axis of the system and have initial unperturbed number densities defined as $n_{0\alpha }$![]() with $\alpha = 1, 2$
with $\alpha = 1, 2$![]() denoting the electron species. The ion background has density $n_i = \sum _\alpha n_{0\alpha }$
denoting the electron species. The ion background has density $n_i = \sum _\alpha n_{0\alpha }$![]() which neutralises the global electron charge of the system. The global net current density is zero. The initial unperturbed electron beam velocities are defined as $v_{0x\alpha }$
which neutralises the global electron charge of the system. The global net current density is zero. The initial unperturbed electron beam velocities are defined as $v_{0x\alpha }$![]() with their three-momenta given by $\boldsymbol {v_\alpha } = c \boldsymbol {p_\alpha }/(m^2c^2 + p^2_\alpha )^{1/2}$
with their three-momenta given by $\boldsymbol {v_\alpha } = c \boldsymbol {p_\alpha }/(m^2c^2 + p^2_\alpha )^{1/2}$![]() . All variables are assumed to depend on $y$
. All variables are assumed to depend on $y$![]() and time. From this, the relativistic dynamics of the electrons are described by the following equations with $\boldsymbol {A}$
and time. From this, the relativistic dynamics of the electrons are described by the following equations with $\boldsymbol {A}$![]() the vector potential field defined by the magnetic field $\boldsymbol {B} = \boldsymbol {\nabla } \times \boldsymbol {A}$
the vector potential field defined by the magnetic field $\boldsymbol {B} = \boldsymbol {\nabla } \times \boldsymbol {A}$![]() :
:
The electron momenta and densities are coupled with the following Maxwell's equations (Griffiths Reference Griffiths2013):

Maxwell's equations and relativistic dynamics equations are linearised using a plane-wave approximation of the form $\sim \exp (-{\rm i}\omega t + {\rm i}ky)$![]() for the velocities, densities and fields with $\omega$
for the velocities, densities and fields with $\omega$![]() being the perturbation angular frequency and $k$
being the perturbation angular frequency and $k$![]() the perturbation wavevector. The applied transverse electric perturbation field is given by $\boldsymbol {E_{1}} = E_0 \exp (-{\rm i}\omega t + {\rm i}ky) \hat {\boldsymbol {x}}$
the perturbation wavevector. The applied transverse electric perturbation field is given by $\boldsymbol {E_{1}} = E_0 \exp (-{\rm i}\omega t + {\rm i}ky) \hat {\boldsymbol {x}}$![]() . In this linearisation process, the following operations become ${\partial }/{\partial t} \rightarrow -{\rm i}\omega$
. In this linearisation process, the following operations become ${\partial }/{\partial t} \rightarrow -{\rm i}\omega$![]() and $\boldsymbol {\nabla } \rightarrow {\rm i}k \hat {\boldsymbol {y}}$
and $\boldsymbol {\nabla } \rightarrow {\rm i}k \hat {\boldsymbol {y}}$![]() for ease. It is found that the first-order components for these variables give the following:
for ease. It is found that the first-order components for these variables give the following:

When the above definitions of the first-order quantities are introduced into (2.7) with the substitution of (2.5), a sixth-order dispersion relation is found for mode frequency $\omega$![]() and perturbation wavevector $k$
and perturbation wavevector $k$![]() :
:
where

with the non-relativistic plasma frequency $\omega _{\textrm {pe}} \equiv (4{\rm \pi} e^2 n_i/m)^{1/2}$![]() and the Lorentz factor $\varGamma _\alpha = (1 - v_{0x\alpha }^2/c^2)^{-1/2}$
and the Lorentz factor $\varGamma _\alpha = (1 - v_{0x\alpha }^2/c^2)^{-1/2}$![]() . The dispersion relation in (2.12) can be solved by a substitution of variables, $u = \omega ^2$
. The dispersion relation in (2.12) can be solved by a substitution of variables, $u = \omega ^2$![]() , reducing the sextic dispersion relation to a cubic equation. This cubic equation can be solved numerically with numpy.roots function in Python. This function involves computing the eigenvalues of the companion matrix (Johnson & Horn Reference Johnson and Horn1985).
, reducing the sextic dispersion relation to a cubic equation. This cubic equation can be solved numerically with numpy.roots function in Python. This function involves computing the eigenvalues of the companion matrix (Johnson & Horn Reference Johnson and Horn1985).
Three branches can be observed from the solutions to the dispersion relation, two oscillatory modes $(\mathrm {Im} (\omega ) = 0)$![]() and one exponentially growing mode with a non-vanishing imaginary component $(\mathrm {Im} (\omega ) \neq 0)$
and one exponentially growing mode with a non-vanishing imaginary component $(\mathrm {Im} (\omega ) \neq 0)$![]() . The exponentially growing mode is responsible for the Weibel instability. By defining $\omega = \textrm {i}\gamma$
. The exponentially growing mode is responsible for the Weibel instability. By defining $\omega = \textrm {i}\gamma$![]() , the growth rate $\gamma$
, the growth rate $\gamma$![]() can be calculated from the exponentially growing mode as a function of the perturbation wavevector $k$
can be calculated from the exponentially growing mode as a function of the perturbation wavevector $k$![]() . Curves for both non-relativistic and relativistic cases of two counterstreaming electron beams with a neutralising ion background are shown in figure 1, showing the growth rate of the Weibel instability as a function of $k^2$
. Curves for both non-relativistic and relativistic cases of two counterstreaming electron beams with a neutralising ion background are shown in figure 1, showing the growth rate of the Weibel instability as a function of $k^2$![]() .
.

Figure 1. Instability growth rate for both a non-relativistic and relativistic case. The two beams have equal number density, i.e. $n_{0,1} = n_{0,2} = n_i/2$![]() . In general, all dispersion relations follow the same pattern where the growth rate reaches a maximum at short perturbation wavelengths.
. In general, all dispersion relations follow the same pattern where the growth rate reaches a maximum at short perturbation wavelengths.
The maximum growth rate is achieved in the short-wavelength limit where $k^2c^2 \gg \varOmega ^2_a, \varOmega ^2_b, \varOmega ^2_c, \varOmega ^2_d$![]() . When this limit is applied to (2.12), equation (2.14) is returned, which shows no dependence on the wavevector $k$
. When this limit is applied to (2.12), equation (2.14) is returned, which shows no dependence on the wavevector $k$![]() . In the long-wavelength limit where $k^2c^2 \sim 0$
. In the long-wavelength limit where $k^2c^2 \sim 0$![]() , the growth rate follows a linear dependence on the perturbation wavevector $k$
, the growth rate follows a linear dependence on the perturbation wavevector $k$![]() given by (2.15). These limits follow from Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996). The limits are dependent on the $\varOmega ^2_i$
given by (2.15). These limits follow from Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996). The limits are dependent on the $\varOmega ^2_i$![]() terms found in the dispersion relation (2.12), which are determined by the density and beam velocity parameters of the system
terms found in the dispersion relation (2.12), which are determined by the density and beam velocity parameters of the system
The collisional effects between plasma species can be ignored if the electron collision rate is much smaller than the Weibel instability growth rate. The instability growth rate, $\gamma$![]() , can be determined in units of the plasma frequency, giving $\gamma = \gamma _{g} [\omega _{\textrm {pe}}]$
, can be determined in units of the plasma frequency, giving $\gamma = \gamma _{g} [\omega _{\textrm {pe}}]$![]() , where $\gamma _g$
, where $\gamma _g$![]() is the magnitude of the instability growth rate. Using the formulae for the electron collision rate and the electron plasma frequency from the NRL formulary (Huba Reference Huba2013), a condition for the collisional effects to be ignored can be determined,
is the magnitude of the instability growth rate. Using the formulae for the electron collision rate and the electron plasma frequency from the NRL formulary (Huba Reference Huba2013), a condition for the collisional effects to be ignored can be determined,
where $\ln {\varLambda }$![]() is the Coulomb logarithm, $n_e$
is the Coulomb logarithm, $n_e$![]() is the electron number density in units of cm$^{-3}$
is the electron number density in units of cm$^{-3}$![]() and $T_e$
and $T_e$![]() is the electron temperature in units of eV. For example, if $\ln {\varLambda } = 10$
is the electron temperature in units of eV. For example, if $\ln {\varLambda } = 10$![]() and electron density of $n_e = 10^{18} \, \textrm {cm}^{-3}$
and electron density of $n_e = 10^{18} \, \textrm {cm}^{-3}$![]() are assumed whereas the instability growth rate is found to be $\gamma = 10^{-1} \ \omega _{\textrm {pe}}$
are assumed whereas the instability growth rate is found to be $\gamma = 10^{-1} \ \omega _{\textrm {pe}}$![]() , then the electron temperature must be $T_e \gg 10.2 \, \textrm {eV}$
, then the electron temperature must be $T_e \gg 10.2 \, \textrm {eV}$![]() for collisional effects to be ignored. Consequently, collisions are neglected in both the derived theoretical models and PIC simulations. If a low-density plasma is considered, then this model assumption is valid.
for collisional effects to be ignored. Consequently, collisions are neglected in both the derived theoretical models and PIC simulations. If a low-density plasma is considered, then this model assumption is valid.
2.2. Three-electron-populations case
Extending from the work in § 2.1, the case of three electron populations with an immobile proton background is examined and the dispersion relation determined. This case involves two counterstreaming beams of electrons as previously and an additional third cold electron population with zero drift velocity with respect to the immobile proton background. Similarly, the number densities of the three populations must equate the number density of the proton background and net current density in the system is zero. What is found is a dispersion relation with the same functional form as the two-beam case (2.12) with an adjustment to the $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() terms
terms

The population with $\alpha = 3$![]() is the cold background electron population and has been shown explicitly for clarity. These terms therefore depend on the number density of the cold electron background. Here $\varOmega ^2_c$
is the cold background electron population and has been shown explicitly for clarity. These terms therefore depend on the number density of the cold electron background. Here $\varOmega ^2_c$![]() and $\varOmega ^2_d$
and $\varOmega ^2_d$![]() remain unaffected by the background electron population as the drift velocity is $v_{03x} = 0$
remain unaffected by the background electron population as the drift velocity is $v_{03x} = 0$![]() by definition.
by definition.
The largest difference between the two-beam case and the three-populations case occurs in the relativistic regime. In the two-beam case, $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() tend to zero as the Lorentz factors $\varGamma _\alpha$
tend to zero as the Lorentz factors $\varGamma _\alpha$![]() increase due to electron inertia. For the three-population case, $\varOmega ^2_a$
increase due to electron inertia. For the three-population case, $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() follow $\varOmega ^{2}_a \approx \varOmega ^{2}_b \rightarrow \omega ^2_{\textrm {pe}} ({n_{0, 3}}/{n_i})$
follow $\varOmega ^{2}_a \approx \varOmega ^{2}_b \rightarrow \omega ^2_{\textrm {pe}} ({n_{0, 3}}/{n_i})$![]() in the relativistic limit, which is significant if the stationary density is a large fraction of the total electron density.
in the relativistic limit, which is significant if the stationary density is a large fraction of the total electron density.
The perturbation wavelength limits formulae (2.14)–(2.15) were applied to the three-electron-population case by substituting the new $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() terms, this is shown in figure 2(a). A large density ratio of $n_{\textrm {back}}/2n_{\textrm {beam}} = 10$
terms, this is shown in figure 2(a). A large density ratio of $n_{\textrm {back}}/2n_{\textrm {beam}} = 10$![]() is chosen because there is significant change to the original two-electron-beam model used to derive the original limits in Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996). Both the short- and long-wavelength limits still agree with the new dispersion relation for the three-electron-populations case.
is chosen because there is significant change to the original two-electron-beam model used to derive the original limits in Pegoraro et al. (Reference Pegoraro, Bulanov, Califano and Lontano1996). Both the short- and long-wavelength limits still agree with the new dispersion relation for the three-electron-populations case.

Figure 2. Growth rate as a function of the perturbation wavenumber for (a) the three-electron-populations case, and (b) the lepton-beam case and the plasma-flow case, where the short- and long-wavelength limits are shown by the red and green dashed lines, respectively. The three-electron-populations case has a density ratio of $n_{\textrm {back}}/2n_{\textrm {beam}} = 10$![]() and beam Lorentz factors $\varGamma _{\alpha } = 3.57$
and beam Lorentz factors $\varGamma _{\alpha } = 3.57$![]() . The lepton-beam and plasma-flow cases have the parameters $n_j/n_p = 0.5$
. The lepton-beam and plasma-flow cases have the parameters $n_j/n_p = 0.5$![]() and $\varGamma _j = 100$
and $\varGamma _j = 100$![]() . The short-wavelength limit of the lepton-beam case is a factor of $\sqrt {2}$
. The short-wavelength limit of the lepton-beam case is a factor of $\sqrt {2}$![]() larger than the same limit in the plasma-flow case.
larger than the same limit in the plasma-flow case.
There are competing modes for the Weibel instability in the three-electron-population case due to beam–beam and beam–background interactions. This is determined by comparing the dispersion relations of the two-beam, one-beam-on-background and the three-population cases. At high background densities of $2n_{\textrm {back}}/n_{\textrm {beam}} \geq 1$![]() , the beam–background interaction dominates leading to the three-electron-population case to follow the one-beam-on-background case for all $k$
, the beam–background interaction dominates leading to the three-electron-population case to follow the one-beam-on-background case for all $k$![]() values. Meanwhile, at low background densities of $2n_{\textrm {back}}/n_{\textrm {beam}} < 0.01$
values. Meanwhile, at low background densities of $2n_{\textrm {back}}/n_{\textrm {beam}} < 0.01$![]() , the beam–beam interaction dominates leading to the three-electron-population case following the two-beam case for all $k$
, the beam–beam interaction dominates leading to the three-electron-population case following the two-beam case for all $k$![]() values. In the density regime between those endpoints, the beam–background interaction dominates for $k < 1$
values. In the density regime between those endpoints, the beam–background interaction dominates for $k < 1$![]() whereas the beam–beam interaction dominates for $k > 1$
whereas the beam–beam interaction dominates for $k > 1$![]() .
.
In the cold-fluid formalism, the short-wavelength limit, where $k \to \infty$![]() , gives a saturated maximum instability growth rate (Bret et al. Reference Bret, Gremillet and Dieckmann2010). The short-wavelength limit can be analysed analytically to retrieve the scaling with beam velocity and density parameters when working with equal density and speed beams for the three-electron-populations case. For this case, $\varOmega ^2_d = 0$
, gives a saturated maximum instability growth rate (Bret et al. Reference Bret, Gremillet and Dieckmann2010). The short-wavelength limit can be analysed analytically to retrieve the scaling with beam velocity and density parameters when working with equal density and speed beams for the three-electron-populations case. For this case, $\varOmega ^2_d = 0$![]() and (2.14) reduces to
and (2.14) reduces to

where $\gamma$![]() is the maximum growth rate, $\varGamma _b$
is the maximum growth rate, $\varGamma _b$![]() is the beam Lorentz factor, $\beta = v/c$
is the beam Lorentz factor, $\beta = v/c$![]() and $R = n_{\textrm {back}}/2n_{\textrm {beam}}$
and $R = n_{\textrm {back}}/2n_{\textrm {beam}}$![]() . Equation (2.18) can be applied to the low- and high-beam-density regimes to give
. Equation (2.18) can be applied to the low- and high-beam-density regimes to give

which are comparable to the scalings found in table I in Bret et al. (Reference Bret, Gremillet and Dieckmann2010) for electron beams incident on electron–ion plasmas. Consequently, in the three-electron-populations case the maximum growth rate is dependent on the beam-to-background-density ratio and the beam Lorentz factor in the low-beam-density regime. Meanwhile, in the high-beam-density regime the maximum growth rate decouples from the density ratio and is wholly dependent on the beam Lorentz factor.
2.3. Lepton beam and plasma beam cases
The lepton beam into a background plasma case is also examined with a similar linearisation process. The electron–positron beam has both net zero charge density and zero current density, i.e. $n_{ e^-,0j} = n_{e^+,0j} = {n_{0j}}/{2}$![]() and $v_{e^-,0j} = v_{e^+,0j} = v_{0xj}$
and $v_{e^-,0j} = v_{e^+,0j} = v_{0xj}$![]() and is travelling in the positive $x$
and is travelling in the positive $x$![]() direction. The background electron–proton plasma has zero net charge $(n_e = n_p)$
direction. The background electron–proton plasma has zero net charge $(n_e = n_p)$![]() and zero electron drift velocity with the protons being frozen. There is no restriction between the density of the lepton beam and the density of the background electron–proton plasma as individually they satisfy the neutrality requirements. When the linearisation process is applied to Maxwell's equations and the relativistic dynamics equations, a comparable dispersion relation to (2.12) is found albeit with a change in the $\varOmega ^2_i$
and zero electron drift velocity with the protons being frozen. There is no restriction between the density of the lepton beam and the density of the background electron–proton plasma as individually they satisfy the neutrality requirements. When the linearisation process is applied to Maxwell's equations and the relativistic dynamics equations, a comparable dispersion relation to (2.12) is found albeit with a change in the $\varOmega ^2_i$![]() terms which are as follows
terms which are as follows

The terms are normalised to the background electron–proton plasma frequency, in this case $\omega _{\textrm {pe}}$![]() . Similarly to the three-electron-populations case, the $\varOmega ^2_a$
. Similarly to the three-electron-populations case, the $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() terms have a component that is unchanged for differing beam velocities due to the electron density in the background plasma. In the ultrarelativistic limit, $\varOmega ^2_a \approx \varOmega ^2_b \rightarrow \omega ^2_{\textrm {pe}}$
terms have a component that is unchanged for differing beam velocities due to the electron density in the background plasma. In the ultrarelativistic limit, $\varOmega ^2_a \approx \varOmega ^2_b \rightarrow \omega ^2_{\textrm {pe}}$![]() , which means the electron inertia becomes wholly dependent on the electron–proton plasma density.
, which means the electron inertia becomes wholly dependent on the electron–proton plasma density.
The perturbation wavelength limits formulae (2.14)–(2.15) were applied to the lepton-beam case by substituting the new $\varOmega ^2_i$![]() terms, which is shown in figure 2(b). A density ratio of $n_j/n_p = 0.5$
terms, which is shown in figure 2(b). A density ratio of $n_j/n_p = 0.5$![]() is chosen so that the beam density is a significant fraction of the background plasma density, hence the Weibel instability growth rate is appreciable. A beam Lorentz factor of $\varGamma _j = 100$
is chosen so that the beam density is a significant fraction of the background plasma density, hence the Weibel instability growth rate is appreciable. A beam Lorentz factor of $\varGamma _j = 100$![]() is chosen such that model is in the relativistic beam regime. There is great agreement between the short- and long-wavelength limits with the dispersion relation for the lepton-beam case.
is chosen such that model is in the relativistic beam regime. There is great agreement between the short- and long-wavelength limits with the dispersion relation for the lepton-beam case.
For a plasma beam incident on a background electron–proton plasma, the derivation of the dispersion relation follows from the lepton-beam case with the change of positrons to protons in the beam. This means the positive charges within the beam are now approximately 1836 times heavier than the electrons although their initial velocities are equal to maintain current density neutrality. The protons in the flow are not frozen. The $\varOmega ^2_i$![]() terms derived from the dispersion relation are as follows:
terms derived from the dispersion relation are as follows:

with non-relativistic electron and proton plasma frequencies given by $\omega ^2_e = ({4 {\rm \pi}e^2 n_p})/{m_e}$![]() and $\omega ^2_p = ({4 {\rm \pi}e^2 n_p})/{m_p}$
and $\omega ^2_p = ({4 {\rm \pi}e^2 n_p})/{m_p}$![]() , respectively. With respect to the lepton beam $\varOmega ^2_i$
, respectively. With respect to the lepton beam $\varOmega ^2_i$![]() terms, the plasma-flow terms show a factor of 1/2 wherever the density ratio $n_{0j}/n_p$
terms, the plasma-flow terms show a factor of 1/2 wherever the density ratio $n_{0j}/n_p$![]() is found and there is a small addition to all terms due to the perturbation of the protons in the beam $(\omega ^2_e/\omega ^2_p \approx 1836)$
is found and there is a small addition to all terms due to the perturbation of the protons in the beam $(\omega ^2_e/\omega ^2_p \approx 1836)$![]() . The overall behaviour of the dispersion is comparable to the lepton-beam case with the difference in the short-wavelength limit growth rate shown in figure 2(b). The lepton-beam case shows a factor $\sqrt {2}$
. The overall behaviour of the dispersion is comparable to the lepton-beam case with the difference in the short-wavelength limit growth rate shown in figure 2(b). The lepton-beam case shows a factor $\sqrt {2}$![]() increase in the short-wavelength limit growth rate compared with the plasma beam case in the relativistic or low $n_{0j}/n_p$
increase in the short-wavelength limit growth rate compared with the plasma beam case in the relativistic or low $n_{0j}/n_p$![]() density ratio regimes with the same beam Lorentz factors. This is due to the maximum instability growth rate being a function of the density ratio $n_{0j}/n_p$
density ratio regimes with the same beam Lorentz factors. This is due to the maximum instability growth rate being a function of the density ratio $n_{0j}/n_p$![]() as seen in table I of Bret et al. (Reference Bret, Gremillet and Dieckmann2010) in the low-beam-density regime. Therefore, the inherent doubling of the density ratio when comparing the lepton-beam case to the plasma-flow case leads to the $\sqrt {2}$
as seen in table I of Bret et al. (Reference Bret, Gremillet and Dieckmann2010) in the low-beam-density regime. Therefore, the inherent doubling of the density ratio when comparing the lepton-beam case to the plasma-flow case leads to the $\sqrt {2}$![]() factor in maximum growth rate.
factor in maximum growth rate.
3. Comparisons with PIC simulations
3.1. PIC simulations and growth rates
The PIC simulations are performed using the open-source code Smilei (Derouillat et al. Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov and Aunai2018). The simulation box is set with $20 \lambda _k$![]() in both the $x$
in both the $x$![]() and $y$
and $y$![]() directions where $\lambda _k$
directions where $\lambda _k$![]() is the wavelength of the applied electric perturbation field given by $\lambda _k = 2{\rm \pi} /k$
is the wavelength of the applied electric perturbation field given by $\lambda _k = 2{\rm \pi} /k$![]() . The perturbation wavevector $k$
. The perturbation wavevector $k$![]() is normalised to the reference frequency $\omega _r/c$
is normalised to the reference frequency $\omega _r/c$![]() where in the counterstreaming-beam cases, $\omega _r$
where in the counterstreaming-beam cases, $\omega _r$![]() is given by the plasma frequency of all electron populations $\omega ^2_{\textrm {pe}} = 4{\rm \pi} n_{e,total} e^2/m_e$
is given by the plasma frequency of all electron populations $\omega ^2_{\textrm {pe}} = 4{\rm \pi} n_{e,total} e^2/m_e$![]() . In the beam cases, $\omega _r$
. In the beam cases, $\omega _r$![]() is given by the background electron plasma frequency $\omega ^2_{\textrm {pe}} = 4{\rm \pi} n_{p} e^2/m_e$
is given by the background electron plasma frequency $\omega ^2_{\textrm {pe}} = 4{\rm \pi} n_{p} e^2/m_e$![]() . The grid spacing $d$
. The grid spacing $d$![]() for both directions is $\lambda _{k}/8$
for both directions is $\lambda _{k}/8$![]() for most of the simulations and the timestep is half the grid spacing, $\Delta t = 0.5*d/c$
for most of the simulations and the timestep is half the grid spacing, $\Delta t = 0.5*d/c$![]() . The grid spacing $d = \lambda _{k}/16$
. The grid spacing $d = \lambda _{k}/16$![]() is sometimes used to determine the growth rate at low values of $k$
is sometimes used to determine the growth rate at low values of $k$![]() where the timestep becomes too large to resolve the linear regime. The number of particles per cell for both electrons and protons is 256. The boundary conditions for both fields and particles are periodic. Perturbations are applied via a transverse electric field $E_y$
where the timestep becomes too large to resolve the linear regime. The number of particles per cell for both electrons and protons is 256. The boundary conditions for both fields and particles are periodic. Perturbations are applied via a transverse electric field $E_y$![]() of sinusoidal form with wavelength $\lambda _k$
of sinusoidal form with wavelength $\lambda _k$![]() and an amplitude of $0.001 \, m_e c \omega _{\textrm {pe}} /e$
and an amplitude of $0.001 \, m_e c \omega _{\textrm {pe}} /e$![]() in plasma units. With the parameters defined as such, the timestep and grid spacing are different for each perturbation wavevector $k$
in plasma units. With the parameters defined as such, the timestep and grid spacing are different for each perturbation wavevector $k$![]() and this is taken into account when the diagnostics are analysed.
and this is taken into account when the diagnostics are analysed.
The computational Weibel instability growth rates are determined from the electromagnetic energy density diagnostics of the PIC simulations. In CGS units, the electromagnetic energy density is $u = ({1}/{8 {\rm \pi}})(E^2 + B^2)$![]() , using the $B_z$
, using the $B_z$![]() component for the Weibel instability and the introduction of the plane wave perturbation, the following equation can be found
component for the Weibel instability and the introduction of the plane wave perturbation, the following equation can be found
where $u$![]() is the electromagnetic energy density given by $B_z$
is the electromagnetic energy density given by $B_z$![]() , $\gamma$
, $\gamma$![]() is the Weibel instability growth rate, $t$
is the Weibel instability growth rate, $t$![]() is time and $B_0$
is time and $B_0$![]() is the amplitude of the plane wave perturbation derived from Faraday's law (2.6) on the applied perturbative electric field. The gradient of a linear fit to a log plot of $u$
is the amplitude of the plane wave perturbation derived from Faraday's law (2.6) on the applied perturbative electric field. The gradient of a linear fit to a log plot of $u$![]() gives $m = 2\gamma$
gives $m = 2\gamma$![]() , which is used to determine the growth rates of the Weibel instability from the PIC simulations at different values of $k$
, which is used to determine the growth rates of the Weibel instability from the PIC simulations at different values of $k$![]() . These PIC determined growth rates are compared with the growth rates determined from the derived dispersion relations to check the accuracy of the models.
. These PIC determined growth rates are compared with the growth rates determined from the derived dispersion relations to check the accuracy of the models.
3.2. PIC simulations for the three-electron-populations case
In these simulations, the two counterstreaming electron beams are initialised with equal density and magnitude in momentum for the sake of simplicity. In the first set of simulations, the ratio of the counterstreaming beam densities and the background electron population is fixed with $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$![]() . The Lorentz factor for the counterstreaming beams is varied to see its effect on the Weibel instability growth rate. The comparisons between the linear dispersion theory and PIC code determined growth rates are shown in figure 3 along with the maximum growth rate scaling from (2.18). It should be noted that in the non-relativistic regime, the electrostatic field also grows via an instability. The growth rates for both the transverse Weibel instability and the longitudinal electric field instability were found to be similar thereby the majority electromagnetic energy comes from both the transverse magnetic and longitudinal electrostatic fields.
. The Lorentz factor for the counterstreaming beams is varied to see its effect on the Weibel instability growth rate. The comparisons between the linear dispersion theory and PIC code determined growth rates are shown in figure 3 along with the maximum growth rate scaling from (2.18). It should be noted that in the non-relativistic regime, the electrostatic field also grows via an instability. The growth rates for both the transverse Weibel instability and the longitudinal electric field instability were found to be similar thereby the majority electromagnetic energy comes from both the transverse magnetic and longitudinal electrostatic fields.

Figure 3. Instability growth rates for the three-electron-populations case with differing Lorentz factors. The ratio between the added beam densities and the background density is $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$![]() . The beam Lorentz factors are determined from the rest frame of the immobile protons and the crosses are the growth rates in the PIC simulations. The dotted lines give the short-wavelength limit from (2.18).
. The beam Lorentz factors are determined from the rest frame of the immobile protons and the crosses are the growth rates in the PIC simulations. The dotted lines give the short-wavelength limit from (2.18).
Focussing on the Weibel instability growth rate, it shows a strong linear dependence with $k$![]() in the long-wavelength limit, which contrasts with the original two population case in the relativistic regime seen in figure 1. The introduction of the background electron plasma with a comparable density to the beams, which affects the $\varOmega ^2_a$
in the long-wavelength limit, which contrasts with the original two population case in the relativistic regime seen in figure 1. The introduction of the background electron plasma with a comparable density to the beams, which affects the $\varOmega ^2_a$![]() and $\varOmega ^2_b$
and $\varOmega ^2_b$![]() terms, causes the strong linear dependence to remain in this limit. This is due to competing instabilities for the beam–beam interaction and the beam–background interaction. It is found qualitatively that the beam–beam Weibel instability dominates at high $k$
terms, causes the strong linear dependence to remain in this limit. This is due to competing instabilities for the beam–beam interaction and the beam–background interaction. It is found qualitatively that the beam–beam Weibel instability dominates at high $k$![]() values and low background plasma densities, whereas the beam–background Weibel instability dominates at low $k$
values and low background plasma densities, whereas the beam–background Weibel instability dominates at low $k$![]() values and high background plasma densities. For $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$
values and high background plasma densities. For $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$![]() found in figure 3, the beam–background interaction dominates, which produces the strong linear dependence for lower values of $k$
found in figure 3, the beam–background interaction dominates, which produces the strong linear dependence for lower values of $k$![]() . Overall the dispersion relation for this case is slightly overestimating the growth rates determined from the PIC simulations.
. Overall the dispersion relation for this case is slightly overestimating the growth rates determined from the PIC simulations.
The ratio between the counterstreaming beam density and the cold electron background density is changed to see how this would affect the growth rate of the Weibel instability while maintaining the beam Lorentz factor constant. The results from the PIC simulations and comparison with the linear dispersion theory are shown in figure 4 for a non-relativistic and relativistic case. When the background electron population density is small, the functional dependence between the growth rate and $k$![]() shows similar behaviour in the long-wavelength limit as it approximates the relativistic two-counterstreaming-beams case seen in figure 1. This behaviour vanishes when the density of the background electron population is comparable to the beam densities. Again, the dispersion relation is slightly overestimating the PIC determined growth rates.
shows similar behaviour in the long-wavelength limit as it approximates the relativistic two-counterstreaming-beams case seen in figure 1. This behaviour vanishes when the density of the background electron population is comparable to the beam densities. Again, the dispersion relation is slightly overestimating the PIC determined growth rates.

Figure 4. Instability growth rates for (a) a non-relativistic case of $| v_{0x}|= 0.1c$![]() and (b) a relativistic case of $| v_{0x} | = 0.96c$
and (b) a relativistic case of $| v_{0x} | = 0.96c$![]() with density variations defined by the ratio $n_{\textrm {back}}/2n_{\textrm {beam}}$
with density variations defined by the ratio $n_{\textrm {back}}/2n_{\textrm {beam}}$![]() . For the relativistic case, as the density ratio is increased, the growth rate of the instability decreases. In the non-relativistic case, no difference is observed for the density ratios used in the PIC simulations.
. For the relativistic case, as the density ratio is increased, the growth rate of the instability decreases. In the non-relativistic case, no difference is observed for the density ratios used in the PIC simulations.
An example of the transverse magnetic field $B_z$![]() progression for the three-electron- populations case is shown in figure 5. At the earlier stages of the PIC simulation, filamentation occurs which causes the bands seen in the first figure. As the magnetic field saturates, the turbulent phase begins causing the filaments to break up. This is more evident in the lepton-beam case.
progression for the three-electron- populations case is shown in figure 5. At the earlier stages of the PIC simulation, filamentation occurs which causes the bands seen in the first figure. As the magnetic field saturates, the turbulent phase begins causing the filaments to break up. This is more evident in the lepton-beam case.

Figure 5. Snapshots of $B_z$![]() magnetic field from PIC simulations for the three-population-case at (a) $t= 235.6 \, \omega ^{-1}_{\textrm {pe}}$
magnetic field from PIC simulations for the three-population-case at (a) $t= 235.6 \, \omega ^{-1}_{\textrm {pe}}$![]() and (b) $t = 4712.4 \, \omega ^{-1}_{\textrm {pe}}$
and (b) $t = 4712.4 \, \omega ^{-1}_{\textrm {pe}}$![]() . The beam Lorentz factor is $\varGamma = 2$
. The beam Lorentz factor is $\varGamma = 2$![]() , wavevector $k = 0.2$
, wavevector $k = 0.2$![]() and density ratio $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$
and density ratio $n_{\textrm {back}}/2n_{\textrm {beam}} = 0.5$![]() . All quantities are in plasma units.
. All quantities are in plasma units.
3.3. PIC simulations for lepton and plasma beams into background electron–proton plasma
The effect of the Lorentz factor on the Weibel instability growth rate is explored by fixing a beam-to-background density ratio and varying the Lorentz factor. The comparison between the PIC growth rates and the dispersion relations are shown in figure 6(a). The functional dependence between the growth rate and $k$![]() in the long-wavelength limit follows from the non-relativistic two-counterstreaming-beams case even with high beam Lorentz factors. This shows that the behaviour in the relativistic two-counterstreaming-beams case in the long-wavelength limit is unique amongst all the models explored here. The short-wavelength limit shows inverse proportionality to the square root of the beam Lorentz factor as expected from a cold fluid approximation.
in the long-wavelength limit follows from the non-relativistic two-counterstreaming-beams case even with high beam Lorentz factors. This shows that the behaviour in the relativistic two-counterstreaming-beams case in the long-wavelength limit is unique amongst all the models explored here. The short-wavelength limit shows inverse proportionality to the square root of the beam Lorentz factor as expected from a cold fluid approximation.

Figure 6. Instability growth rates compared with PIC simulations for the lepton-beam case and plasma-flow case. (a) Relation between the growth rates and the beam Lorentz factor. The ratio between the beam density and the background density is fixed at $n_{j}/n_{p} = 0.5$![]() . The maximum instability growth rate is inversely proportional to $\sqrt {\varGamma _j}$
. The maximum instability growth rate is inversely proportional to $\sqrt {\varGamma _j}$![]() . (b) Relation between the growth rates and the density ratio. The beam Lorentz factor is fixed at $\varGamma _j = 35.36$
. (b) Relation between the growth rates and the density ratio. The beam Lorentz factor is fixed at $\varGamma _j = 35.36$![]() . The crosses show the PIC determined growth rates for the lepton-beam case and the circles represent the PIC determined growth rates for the plasma beam case.
. The crosses show the PIC determined growth rates for the lepton-beam case and the circles represent the PIC determined growth rates for the plasma beam case.
Conversely, the beam Lorentz factor is fixed $(\varGamma _j = 35.36)$![]() and the density ratios are varied for both cases. The growth rates from the PIC simulations and the linear dispersion relation are compared in figure 6(b). Regardless of the density ratio between the beam and the background plasma, the growth rate shows the linear dependence in the long-wavelength limit and the maximum growth rate in the short-wavelength limit. Furthermore, the maximum growth rate is proportional to $\sqrt {n_j/n_p}$
and the density ratios are varied for both cases. The growth rates from the PIC simulations and the linear dispersion relation are compared in figure 6(b). Regardless of the density ratio between the beam and the background plasma, the growth rate shows the linear dependence in the long-wavelength limit and the maximum growth rate in the short-wavelength limit. Furthermore, the maximum growth rate is proportional to $\sqrt {n_j/n_p}$![]() The dispersion relation shows good agreement with the PIC determined growth rates.
The dispersion relation shows good agreement with the PIC determined growth rates.
From the above, the linear dispersion relation is accurate in determining growth rates for a lepton beam inbound on a background electron–proton plasma and a plasma beam on a background electron–proton plasma. Furthermore, the lepton-beam case shows greater Weibel instability growth rates compared with the plasma beam case by a factor of $\sqrt {2}$![]() in most cases as can be seen in figure 2(b). This is explained by the doubling of the beam-to-background-density ratio between the lepton-beam and electron–proton-beam cases seen in (2.20) and (2.21). The numerical methods used to determine the dispersion relation can be extended to predict Weibel instability growth rates.
in most cases as can be seen in figure 2(b). This is explained by the doubling of the beam-to-background-density ratio between the lepton-beam and electron–proton-beam cases seen in (2.20) and (2.21). The numerical methods used to determine the dispersion relation can be extended to predict Weibel instability growth rates.
An example of the transverse magnetic field $B_z$![]() progression in time for the lepton-beam case is shown in figure 7. At the earlier stages of the PIC simulation, the filamentation occurs and grows exponentially as seen in figure 7(a) as with the three-electron-populations case. As the magnetic field saturates, the turbulent phase is shown clearly where islands of magnetic field intensity are found in figure 7(b).
progression in time for the lepton-beam case is shown in figure 7. At the earlier stages of the PIC simulation, the filamentation occurs and grows exponentially as seen in figure 7(a) as with the three-electron-populations case. As the magnetic field saturates, the turbulent phase is shown clearly where islands of magnetic field intensity are found in figure 7(b).

Figure 7. Snapshots of $B_z$![]() magnetic field from PIC simulations for the lepton-beam case at (a) $t=314.16 \, \omega ^{-1}_{\textrm {pe}}$
magnetic field from PIC simulations for the lepton-beam case at (a) $t=314.16 \, \omega ^{-1}_{\textrm {pe}}$![]() and (b) $1413.72 \, \omega ^{-1}_{\textrm {pe}}$
and (b) $1413.72 \, \omega ^{-1}_{\textrm {pe}}$![]() . The beam Lorentz factor is $\varGamma = 2$
. The beam Lorentz factor is $\varGamma = 2$![]() , wavevector $k = 0.2$
, wavevector $k = 0.2$![]() and density ratio $n_{j}/n_{p} = 0.5$
and density ratio $n_{j}/n_{p} = 0.5$![]() . All quantities are in plasma units.
. All quantities are in plasma units.
3.4. Discussion about the maximum growth rates
Now that the numerical method of determining the modes from the dispersion relation of the Weibel instability has been validated by PIC simulations, it can be used to make some predictions on three-electron-populations and lepton-beam systems. It is shown that the growth rate of the Weibel instability reaches the maximum at the short wavelength limit, which is common to all cases of the dispersion relation. Using this fact, an iterative algorithm is used to find the maximum growth rate for a given beam Lorentz factor and density ratio by scanning logarithmically spaced perturbation wavevectors $k$![]() . A colour map for the three-electron-populations system is shown in figure 8(a), where this maximum growth rate is explored. As the counterstreaming beam density increases, the maximum growth rate increases as intuitively expected. However, as the beam Lorentz factor is increased, a non-monotonic behaviour can be seen. The growth rate peaks at $\varGamma \approx 2$
. A colour map for the three-electron-populations system is shown in figure 8(a), where this maximum growth rate is explored. As the counterstreaming beam density increases, the maximum growth rate increases as intuitively expected. However, as the beam Lorentz factor is increased, a non-monotonic behaviour can be seen. The growth rate peaks at $\varGamma \approx 2$![]() for a high beam density and then decreases as the Lorentz factor is increased.
for a high beam density and then decreases as the Lorentz factor is increased.

Figure 8. Maximum instability growth rate for (a) the three-electron-populations case and(b) the lepton-beam case for various beam Lorentz factors and beam density ratios. The colour bar shows the maximum achievable growth rate with these parameters. The lepton-beam case growth rates show an overall scale of a factor of 10 greater than the three-electron-populations case.
A similar analysis is carried out for the lepton-beam case. The maximum growth rate is explored in the beam Lorentz factor and density ratio space and the colourmap is shown in figure 8(b). The two cases have comparable outcomes. In general, the lepton-beam case shows higher growth rates in the Weibel instability compared with the three-electron-populations case. The highest growth rate achieved is around beam Lorentz factor $\varGamma \approx 10$![]() with the beam density at $10^4$
with the beam density at $10^4$![]() times higher than the background electron–proton plasma.
times higher than the background electron–proton plasma.
The non-monotonic relation between the maximum growth rate and the beam Lorentz factor is explored further. A density ratio of $n_j/n_p = 1 \times 10^3$![]() is fixed and the beam Lorentz factors scanned with a perturbation wavevector of $k = 100$
is fixed and the beam Lorentz factors scanned with a perturbation wavevector of $k = 100$![]() . This ensures the parameters were in the short-wavelength limit so that the maximum growth rate is returned from PIC simulations (see (2.14) and figure 2). The comparison between the PIC determined growth rates and the theoretical dispersion relation are shown in figure 9. The non-monotonic behaviour is clearly present in the dispersion relation and the PIC simulations, with a systematic overestimation by the dispersion relation. Qualitatively, this shows that the Lorentz factor needs to be optimised for a given beam to background plasma density ratio to achieve the highest growth rate possible. In general, this maximum growth rate is achieved at higher beam Lorentz factors as the beam to background plasma density ratio increases as seen in figure 8(b). It should be noted that the plasma-flow case has a comparable relation between the maximum growth rate and the system parameters albeit with a $1/\sqrt {2}$
. This ensures the parameters were in the short-wavelength limit so that the maximum growth rate is returned from PIC simulations (see (2.14) and figure 2). The comparison between the PIC determined growth rates and the theoretical dispersion relation are shown in figure 9. The non-monotonic behaviour is clearly present in the dispersion relation and the PIC simulations, with a systematic overestimation by the dispersion relation. Qualitatively, this shows that the Lorentz factor needs to be optimised for a given beam to background plasma density ratio to achieve the highest growth rate possible. In general, this maximum growth rate is achieved at higher beam Lorentz factors as the beam to background plasma density ratio increases as seen in figure 8(b). It should be noted that the plasma-flow case has a comparable relation between the maximum growth rate and the system parameters albeit with a $1/\sqrt {2}$![]() reduction in maximum growth rate in the relativistic or low-density regimes as explained in § 2.3, which is not shown in this figure.
reduction in maximum growth rate in the relativistic or low-density regimes as explained in § 2.3, which is not shown in this figure.

Figure 9. Non-monotonic behaviour of the maximum Weibel instability growth rate at a density ratio of $n_j/n_p = 10^3$![]() . The PIC simulations were performed with perturbation wavevector $k = 100$
. The PIC simulations were performed with perturbation wavevector $k = 100$![]() to ensure the short-wavelength limit is valid. The dispersion relation for the lepton-beam case is slightly overestimating the maximum growth rates compared with those observed in the PIC simulations.
to ensure the short-wavelength limit is valid. The dispersion relation for the lepton-beam case is slightly overestimating the maximum growth rates compared with those observed in the PIC simulations.
4. Summary and discussion
A theoretical model has been developed for the Weibel instability in three systems, one with two counterpropagating electron beams in background electron–proton plasma, another with a lepton beam propagating in background electron–proton plasma and the final system for a plasma beam propagating in background electron–proton plasma. The dispersion relations have been derived and found to match PIC simulations with good accuracy. There is a general small systematic overestimation of the Weibel instability growth rate from the dispersion relations. Moreover, non-monotonic behaviour has been found in both the theoretical dispersion relations and PIC simulations.
The frozen proton/ion background is a useful approximation for determining the linear dispersion relation, but on longer time scales this breaks down and the approximation is no longer true when the instability develops into the nonlinear stage. Coupled with this is the exclusion of any potential ion acceleration mechanisms induced by the possible development of turbulent fields via the Weibel instability. Longitudinal electrostatic fields can compete with the growth of the Weibel instability in certain regimes (Califano et al. Reference Califano, Pegoraro and Bulanov1997; Silva et al. Reference Silva, Fonseca, Tonge, Mori and Dawson2002; Shaisultanov, Lyubarsky & Eichler Reference Shaisultanov, Lyubarsky and Eichler2011), but have they largely been ignored in this study as the transverse dispersion equations can still accurately describe the growth rates of the Weibel instability. In the leptonic-beam case, it has been shown that there is a preferential positron acceleration through a quasi-stationary electric field and that ion motion could be included in this effect for longer time scales (Dieckmann et al. Reference Dieckmann, Spencer, Falk and Rowlands2020). Further studies are needed with the inclusion of the free motion of the ion background with a focus on the nonlinear stages while looking at the relation between the beam and background densities. The turbulent properties of the long-time-scale Weibel-induced magnetic fields also need to be explored.
Furthermore, Smilei works in dimensionless units with relative quantities. If collisions are included, then a reference plasma frequency must be set thereby setting a reference plasma density. Hence, the models explored in this paper are valid if a low-density plasma is studied as collisions between plasma species will be negligible in that case as minimum electron temperature will be low, as seen in (2.16). However, the relatively cold background electrons and proton/ions compared with the hot beams will have a strong collisional effect when the reference plasma density is set high. Exploring the interplay of temperature and plasma density on the collisional effect on the models is warranted.
Acknowledgements
C.D. would like to acknowledge STFC for the studentship provided to cover doctoral studies.
Editor A.C. Bret thanks the referees for their advice in evaluating this article.
All data underpinning this publication are openly available from the University of Strathclyde KnowledgeBase at https://doi.org/10.15129/12a928e7-f652-4081-a3e9-d095f41506f2
Funding
The authors acknowledge the United Kingdom Science and Technology Facilities Council Grant No. ST/P002056/1. The numerical simulations were carried out on ARCHER via the Plasma HEC Consortium supported by EPSRC Grant Nos. EP/L000237/1 and EP/R029148/1.
Declaration of interests
The authors report no conflict of interest.