1 Introduction
Hybrid plasma models with Boltzmann electrons and space-charge effects (Vu Reference Vu1996; Cartwright, Verboncoeur & Birdsall Reference Cartwright, Verboncoeur and Birdsall2000; Tajima Reference Tajima2018) constitute an important class of plasma models. In these models, the electron density is directly determined from the potential via the Boltzmann relation, and space-charge effects are included via the Poisson equation. The electrostatic hybrid model with Boltzmann electrons and space-charge effects (HBS model) has many applications in plasma physics. The acceleration of light and heavy ions in an expanding plasma slab with hot electrons produced by an intense and short laser pulse is studied using the HBS model by Bychenkov et al. (Reference Bychenkov, Novikov, Batani, Tikhonchuk and Bochkarev2004). Hu & Wang (Reference Hu and Wang2018), by numerical simulations of the HBS model, investigate the expansion of a collisionless hypersonic plasma plume into a vacuum. Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997) numerically simulates resonantly excited nonlinear ion waves using the HBS model and it is noted that the exponential term in the Poisson equation introduces sufficient nonlinearity, allowing us to derive the dispersion relation for parametric instabilities and describe the generation of the second harmonic. Mathematically, a related model with Boltzmann electrons is derived and proved to be well-posed globally by Bardos et al. (Reference Bardos, Golse, Nguyen and Sentis2018). To include electromagnetic effects, an electromagnetic hybrid model with the self-consistent ponderomotive driving potential is proposed by Vu (Reference Vu1996), and a more general fully kinetic, reduced-description particle-in-cell model is presented by Vu, Bezzerides & DuBois (Reference Vu, Bezzerides and DuBois1999) for the ion-driven parametric instabilities.
Different from the fully kinetic (for both ions and electrons) Vlasov–Poisson system, there is no electron distribution function in the HBS model. The simulations using the HBS model allow time step sizes on the scale of ions and are thus more efficient. By taking the quasi-neutral limit of the HBS model, a simplified hybrid model without the space-charge effects (Rambo Reference Rambo1995) can be derived. However, the space-charge effects are important and need to be incorporated in some cases (Vu Reference Vu1996), such as in the inertial confined fusion regime where $k\lambda _e = \mathcal {O}(1)$![]() , with $\lambda _e$
, with $\lambda _e$![]() the electron Debye length and $k$
the electron Debye length and $k$![]() the wavenumber. To achieve accurate resolution at the electron Debye scale, for example, to recover numerically the $k^2 \lambda _e^2$
the wavenumber. To achieve accurate resolution at the electron Debye scale, for example, to recover numerically the $k^2 \lambda _e^2$![]() term in the dispersion relation of the ion acoustic waves, the mesh size $\Delta x$
term in the dispersion relation of the ion acoustic waves, the mesh size $\Delta x$![]() must satisfy $\Delta x < \lambda _e$
must satisfy $\Delta x < \lambda _e$![]() .
.
There have been numerous numerical methods developed for electrostatic plasma models, such as Eulerian methods (Heath et al. Reference Heath, Gamba, Morrison and Michler2012; Manzini et al. Reference Manzini, Delzanno, Vencels and Markidis2016), particle-in-cell methods (Birdsall & Langdon Reference Birdsall and Langdon2018; Hockney & Eastwood Reference Hockney and Eastwood2021) and semi-Lagrangian methods (Cheng & Knorr Reference Cheng and Knorr1976; Sonnendrücker et al. Reference Sonnendrücker, Roche, Bertrand and Ghizzo1999). Recently, some structure-preserving methods have been proposed by Webb (Reference Webb2016) and Gu, He & Sun (Reference Gu, He and Sun2022) for the fully kinetic Vlasov–Poisson system. Structure-preserving methods for the hybrid model with quasi-neutrality and Boltzmann electrons have been developed based on variational or Hamiltonian formulations (Xiao & Qin Reference Xiao and Qin2019a; Li et al. Reference Li, Campos-Pinto, Holderied, Possanner and Sonnendrücker2024a,Reference Li, Holderied, Possanner and Sonnendrückerb). The nonlinear Poisson–Boltzmann equation in the HBS model appears in many electrostatic models in biomolecular simulations. For a review about fast analytical methods, see Xu & Cai (Reference Xu and Cai2011), and for numerical methods, see Lu et al. (Reference Lu, Zhou, Holst and McCammon2008). Many numerical methods have been proposed for the Poisson–Boltzmann equation, such as the finite element method (Chen, Holst & Xu Reference Chen, Holst and Xu2007) and the iterative discontinuous Galerkin method (Yin, Huang & Liu Reference Yin, Huang and Liu2014, Reference Yin, Huang and Liu2018).
In this work, our discretizations of the HBS model follow the structure-preserving methods for models in plasma physics (Qin et al. Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2015b; Xiao et al. Reference Xiao, Qin, Liu, He, Zhang and Sun2015; He et al. Reference He, Sun, Qin and Liu2016; Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017; Morrison Reference Morrison2017), which preserve the geometric structures of the systems and exhibit very good long-term behaviour (Hairer, Lubich & Wanner Reference Hairer, Lubich and Wanner2006; Feng & Qin Reference Feng and Qin2010). The numerical schemes constructed in this work complement existing structure-preserving methods for other (hybrid) electrostatic models. Moreover, a more complicated electromagnetic hybrid model proposed by Vu (Reference Vu1996) is investigated.
The action integral and Hamiltonian structure of the HBS model in this work are derived based on the results of Low (Reference Low1958), Morrison (Reference Morrison1980) and Xiao & Qin (Reference Xiao and Qin2019a). By discretizing the action integral, as done by Xiao et al. (Reference Xiao, Qin, Liu, He, Zhang and Sun2015) and Xiao & Qin (Reference Xiao and Qin2019a), or the Poisson bracket, as done by Qin et al. (Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2015b) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017) with particle methods for the distribution function and finite difference methods for the electrostatic potential, we obtain a finite dimensional Hamiltonian system. Time discretizations are conducted using the Hamiltonian splitting methods (Hairer et al. Reference Hairer, Lubich and Wanner2006) and the discrete gradient methods (Gonzalez Reference Gonzalez1996; McLachlan, Quispel & Robidoux Reference McLachlan, Quispel and Robidoux1999). In plasma physics simulations, Hamiltonian splitting methods have been used by Crouseilles, Einkemmer & Faou (Reference Crouseilles, Einkemmer and Faou2015), Qin et al. (Reference Qin, He, Zhang, Liu, Xiao and Wang2015a), He et al. (Reference He, Qin, Sun, Xiao, Zhang and Liu2015) and discrete gradient methods have been used by Kormann & Sonnendrücker (Reference Kormann and Sonnendrücker2021) as time integrators. For the electromagnetic hybrid model (Vu Reference Vu1996), a Poisson bracket is proposed as the sum of the Lie–Poisson bracket (Morrison Reference Morrison1980) and the canonical bracket of the Schrödinger equation (Marsden & Ratiu Reference Marsden and Ratiu2013).
The neutrality condition is preserved by the discretizations of the HBS model with appropriate boundary conditions. Moreover, we demonstrate that the quasi-neutral limits of the schemes proposed are structure preserving for the hybrid model with quasi-neutrality and Boltzmann electrons. The numerical methods are validated by the good conservation of energy. We conduct the implementation in the Python package STRUPHY (Holderied, Possanner & Wang Reference Holderied, Possanner and Wang2021).
The paper is organized as follows. In § 2, the action integral and the Poisson bracket are presented for the HBS model. In § 3, structure-preserving discretizations are given. In § 4, two asymptotic limits and the dispersion relation of the linear Landau damping of the HBS model are discussed. Geometric structure and discretization of the electromagnetic hybrid model proposed by Vu (Reference Vu1996) are presented in § 5. In § 6, numerical experiments of finite grid instability, Landau damping and resonantly excited nonlinear ion waves are conducted to validate the numerical schemes of the HBS model. In § 7, we conclude the paper with a summary and an outlook for future works.
2 The electrostatic hybrid plasma model with Boltzmann electrons and space-charge effects
In this section, we introduce the action integral and the Poisson bracket for the HBS model (Tajima Reference Tajima2018), and formulate the model as a Hamiltonian system (Hairer et al. Reference Hairer, Lubich and Wanner2006). The electromagnetic hybrid model proposed by Vu (Reference Vu1996) is presented in § 5. The HBS model with physical units is
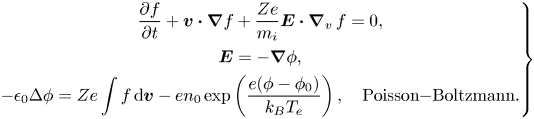
Here, $f(t, {\boldsymbol {x}}, {\boldsymbol {v}})$![]() represents the distribution function of ions, which depends on time $t$
represents the distribution function of ions, which depends on time $t$![]() , position ${\boldsymbol {x}}$
, position ${\boldsymbol {x}}$![]() and velocity ${\boldsymbol {v}}$
and velocity ${\boldsymbol {v}}$![]() . The symbol $e$
. The symbol $e$![]() denotes the unit charge, $m_i$
denotes the unit charge, $m_i$![]() denotes the ion mass and $Z$
denotes the ion mass and $Z$![]() denotes the ion charge number. The electrostatic potential $\phi (t, {\boldsymbol {x}})$
denotes the ion charge number. The electrostatic potential $\phi (t, {\boldsymbol {x}})$![]() is determined by the Poisson–Boltzmann equation and electron density $n_e$
is determined by the Poisson–Boltzmann equation and electron density $n_e$![]() is related to $\phi$
is related to $\phi$![]() through the Boltzmann relation,
through the Boltzmann relation,
where $n_0(t,{\boldsymbol {x}})$![]() is the reference electron number density, $\phi _0(t, {\boldsymbol {x}})$
is the reference electron number density, $\phi _0(t, {\boldsymbol {x}})$![]() is the reference potential or the low-frequency ponderomotive potential and $T_e(t, {\boldsymbol {x}})$
is the reference potential or the low-frequency ponderomotive potential and $T_e(t, {\boldsymbol {x}})$![]() is the given temperature of electrons.
is the given temperature of electrons.
The normalization is done as
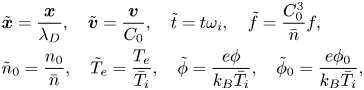
where $C_0 = \sqrt {{k_B \bar {T}_i}/{m_i}}$![]() is the ion thermal speed, $Z\omega _i = \sqrt {{\bar {n} Z^2 e^2}/{\epsilon _0 m_i}}$
is the ion thermal speed, $Z\omega _i = \sqrt {{\bar {n} Z^2 e^2}/{\epsilon _0 m_i}}$![]() is the ion plasma frequency, $\lambda _D = C_0/\omega _i = \sqrt {{\epsilon _0 k_B \bar {T}_i}/{\bar {n} e^2}}$
is the ion plasma frequency, $\lambda _D = C_0/\omega _i = \sqrt {{\epsilon _0 k_B \bar {T}_i}/{\bar {n} e^2}}$![]() , $\bar {n}$
, $\bar {n}$![]() is the characteristic ion density and $\bar {T}_i$
is the characteristic ion density and $\bar {T}_i$![]() is the characteristic ion temperature. Then, we get the normalized HBS model (tilde symbol is omitted for convenience)
is the characteristic ion temperature. Then, we get the normalized HBS model (tilde symbol is omitted for convenience)
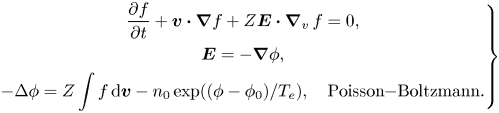
When a periodic or zero Neumann boundary condition is imposed, the HBS model satisfies a neutrality condition given by
To construct structure-preserving methods for this model, the following action integral and Poisson bracket are proposed. For convenience, we consider the case with time independent $n_0, \phi _0, T_e$![]() . The time dependent case can be addressed using the technique of extending the dimension (Zhou et al. Reference Zhou, He, Sun, Liu and Qin2017).
. The time dependent case can be addressed using the technique of extending the dimension (Zhou et al. Reference Zhou, He, Sun, Liu and Qin2017).
Variational principle. By adding the term $\tfrac {1}{2} |\boldsymbol {\nabla } \phi |^2$![]() in Low's action principle (Low Reference Low1958) and combining it with the action principle proposed by Xiao & Qin (Reference Xiao and Qin2019a), we derive the following action integral:
in Low's action principle (Low Reference Low1958) and combining it with the action principle proposed by Xiao & Qin (Reference Xiao and Qin2019a), we derive the following action integral:
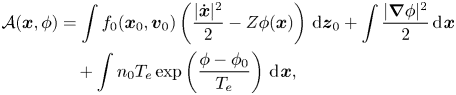
where $\mathrm {d}{{\boldsymbol {z}}_0} := \mathrm {d}{{\boldsymbol {x}}_0}\,\mathrm {d}{{\boldsymbol {v}}_0}$![]() , ${\boldsymbol {x}} ={\boldsymbol {x}}({\boldsymbol {x}}_0, {\boldsymbol {v}}_0, t)$
, ${\boldsymbol {x}} ={\boldsymbol {x}}({\boldsymbol {x}}_0, {\boldsymbol {v}}_0, t)$![]() , and $\dot {\boldsymbol {x}} =\mathrm {d}{\boldsymbol {x}}({\boldsymbol {x}}_0, {\boldsymbol {v}}_0, t)/\mathrm {d}t$
, and $\dot {\boldsymbol {x}} =\mathrm {d}{\boldsymbol {x}}({\boldsymbol {x}}_0, {\boldsymbol {v}}_0, t)/\mathrm {d}t$![]() . We introduce ${\boldsymbol {v}} = \dot {\boldsymbol {x}}$
. We introduce ${\boldsymbol {v}} = \dot {\boldsymbol {x}}$![]() and $f(t, {\boldsymbol {x}}, {\boldsymbol {v}}) = f_0({\boldsymbol {x}}_0, {\boldsymbol {v}}_0)$
and $f(t, {\boldsymbol {x}}, {\boldsymbol {v}}) = f_0({\boldsymbol {x}}_0, {\boldsymbol {v}}_0)$![]() , and the Euler–Lagrangian equations ${\delta \mathcal {A}}/{\delta {\boldsymbol {x}}} = 0, {\delta \mathcal {A}}/{\delta \phi } = 0$
, and the Euler–Lagrangian equations ${\delta \mathcal {A}}/{\delta {\boldsymbol {x}}} = 0, {\delta \mathcal {A}}/{\delta \phi } = 0$![]() can be written as
can be written as
which yields the HBS model (2.4) by calculating ${\mathrm {d}f}/{\mathrm {d}t} = 0$![]() .
.
Poisson bracket. The Poisson bracket of this model is the same as the Vlasov–Poisson system's Poisson bracket proposed by Morrison (Reference Morrison1980),
where $[g, h]_{xv} = \boldsymbol {\nabla }_{\boldsymbol {x}} g \boldsymbol {\cdot } \boldsymbol {\nabla }_{\boldsymbol {v}} h - \boldsymbol {\nabla }_{\boldsymbol {x}} h \boldsymbol {\cdot } \boldsymbol {\nabla }_{\boldsymbol {v}} g$![]() . The Hamiltonian (total energy) of this model is
. The Hamiltonian (total energy) of this model is
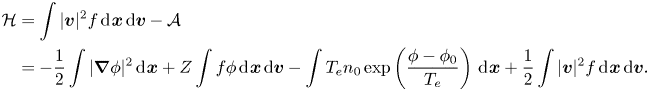
Based on the bracket and Hamiltonian, the HBS model (2.4) can be formulated as
Here, we regard $f$![]() as the only unknown of the HBS model (2.4) and $\phi$
as the only unknown of the HBS model (2.4) and $\phi$![]() is determined by $f$
is determined by $f$![]() from the Poisson–Boltzmann equation in (2.4).
from the Poisson–Boltzmann equation in (2.4).
3 Discretization
We use the particle-in-cell methods to discretize the distribution function $f$![]() and finite difference methods to discretize the electrostatic potential $\phi$
and finite difference methods to discretize the electrostatic potential $\phi$![]() . Two equivalent structure-preserving phase-space discretizations are obtained by discretizing the action integral and the Poisson bracket. The Hamiltonian splitting method and the discrete gradient method are used for time discretizations to preserve the geometric structure and energy, respectively. In the following, $a^n$
. Two equivalent structure-preserving phase-space discretizations are obtained by discretizing the action integral and the Poisson bracket. The Hamiltonian splitting method and the discrete gradient method are used for time discretizations to preserve the geometric structure and energy, respectively. In the following, $a^n$![]() and $a^{n+1}$
and $a^{n+1}$![]() represent the approximations of $a$
represent the approximations of $a$![]() at times $n\Delta t$
at times $n\Delta t$![]() and $(n+1)\Delta t$
and $(n+1)\Delta t$![]() , respectively, and $a^{n+{1}/{2}} = ({ a^{n} + a^{n+1} })/{2}$
, respectively, and $a^{n+{1}/{2}} = ({ a^{n} + a^{n+1} })/{2}$![]() , where $\Delta t$
, where $\Delta t$![]() is the time step size.
is the time step size.
3.1 Discretization of $f$ and $\phi$
and $\phi$
Here, we focus on the one-dimensional case with a periodic boundary condition, but higher dimensional cases can be treated similarly. The distribution function $f$![]() is approximated as
is approximated as
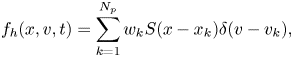
where $N_p$![]() is the total particle number, and $w_k$
is the total particle number, and $w_k$![]() , ${x}_k$
, ${x}_k$![]() and ${v}_k$
and ${v}_k$![]() denote the weight, position and velocity of the $k$
denote the weight, position and velocity of the $k$![]() th particle. Additionally, $S$
th particle. Additionally, $S$![]() is the shape function of the particle, typically chosen as a B-spline. We use the vector ${\boldsymbol {X}}$
is the shape function of the particle, typically chosen as a B-spline. We use the vector ${\boldsymbol {X}}$![]() to denote $(x_1, \ldots, x_{N_p})^\top$
to denote $(x_1, \ldots, x_{N_p})^\top$![]() and vector ${\boldsymbol {V}}$
and vector ${\boldsymbol {V}}$![]() to denote $(v_1, \ldots, v_{N_p})^\top$
to denote $(v_1, \ldots, v_{N_p})^\top$![]() .
.
The electrostatic potential $\phi$![]() is discretized using the finite difference method, i.e.
is discretized using the finite difference method, i.e.
with a set of uniform grids $\{ {x}_j \}$![]() , $N$
, $N$![]() is the number of grids, $(\phi _1, \ldots, \phi _N)^\top$
is the number of grids, $(\phi _1, \ldots, \phi _N)^\top$![]() is denoted as ${\boldsymbol {\phi }}$
is denoted as ${\boldsymbol {\phi }}$![]() and $(\phi _0(x_1), \ldots, \phi _0(x_N))^\top$
and $(\phi _0(x_1), \ldots, \phi _0(x_N))^\top$![]() is denoted as ${\boldsymbol {\phi }}_0$
is denoted as ${\boldsymbol {\phi }}_0$![]() .
.
3.2 Phase-space discretization
3.2.1 Discretization of action integral
We approximate the variational action integral (2.6) as
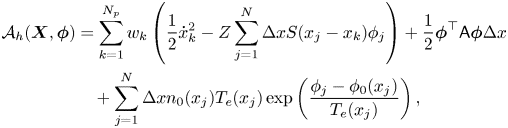
where the matrix $\boldsymbol{\mathsf{A}}$![]() of size $N \times N$
of size $N \times N$![]() is
is

By calculating the variations about ${x}_k$![]() and ${\boldsymbol {\phi }}$
and ${\boldsymbol {\phi }}$![]() , we have
, we have
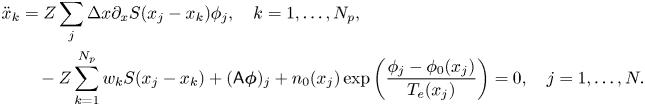
Remark 3.1 The fixed point iteration method of Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997) is used for solving the above discretized Poisson–Boltzmann equation, i.e. the second equation of (3.5),
where $m$![]() is the iteration index, the linear system in iteration $m \rightarrow m+1$
is the iteration index, the linear system in iteration $m \rightarrow m+1$![]() is solved by the conjugate gradient method Kelley (Reference Kelley1995), ${\boldsymbol {n}}_i$
is solved by the conjugate gradient method Kelley (Reference Kelley1995), ${\boldsymbol {n}}_i$![]() is the ion density at grids and the electron density at the $j$
is the ion density at grids and the electron density at the $j$![]() -grid is
-grid is
The initial value of the fixed point iteration is set as zero in § 6.
Equation (3.5) can be formulated as a Hamiltonian system by the Legendre transformation (Marsden & Ratiu Reference Marsden and Ratiu2013). In the following, we present another way to derive a finite dimensional Hamiltonian system.
3.2.2 Discretization of Poisson bracket
Here, we discretize the Poisson bracket (2.8) according to Qin et al. (Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2015b), Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017) and obtain

The discrete Hamiltonian is
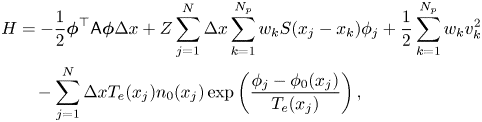
where the ${\boldsymbol {\phi }}$![]() is determined by the particles via the second equation in (3.5). Then, we can obtain the following finite dimensional Hamiltonian system after phase-space discretization:
is determined by the particles via the second equation in (3.5). Then, we can obtain the following finite dimensional Hamiltonian system after phase-space discretization:
The following theorem shows that the discretizations of the action principle and the Poisson bracket as above are equivalent.
Proof. As we know that $\partial _{v_k}H = w_k {v}_k$![]() , we have $\dot {x}_k = v_k$
, we have $\dot {x}_k = v_k$![]() . To obtain (3.5), the only thing we need to prove is that $\partial _{x_k}H = - Z w_k \sum _{j=1}^N \Delta x \partial _x S({x}_j - {x}_k) \phi _j$
. To obtain (3.5), the only thing we need to prove is that $\partial _{x_k}H = - Z w_k \sum _{j=1}^N \Delta x \partial _x S({x}_j - {x}_k) \phi _j$![]() , which is obtained by calculating $\partial _{x_k}H$
, which is obtained by calculating $\partial _{x_k}H$![]() with the discrete Poisson–Boltzmann equation (the second equation in (3.5)),
with the discrete Poisson–Boltzmann equation (the second equation in (3.5)),

where the sum of the last three terms is zero because of the discrete Poisson–Boltzmann equation (the second equation in (3.5)).
Proof. Taking the sum over $j$![]() in the discrete Poisson–Boltzmann equation (the second equation in (3.5)) gives
in the discrete Poisson–Boltzmann equation (the second equation in (3.5)) gives

where we use that $\sum _j (\boldsymbol{\mathsf{A}} {\boldsymbol {\phi }})_j = 0$![]() . This proves the discrete neutrality.
. This proves the discrete neutrality.
3.3 Time discretization
In this subsection, we introduce the time discretizations for (3.5) and (3.10). The first method is the Hamiltonian splitting method (Hairer et al. Reference Hairer, Lubich and Wanner2006), which is explicit and symplectic for (3.5) and (3.10). This method was applied by Crouseilles et al. (Reference Crouseilles, Einkemmer and Faou2015), Qin et al. (Reference Qin, He, Zhang, Liu, Xiao and Wang2015a) and He et al. (Reference He, Qin, Sun, Xiao, Zhang and Liu2015) for the Vlasov–Maxwell equations, and was used by Xiao et al. (Reference Xiao, Qin, Liu, He, Zhang and Sun2015), He et al. (Reference He, Sun, Qin and Liu2016) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017) for the construction of the fully discrete structure-preserving methods. The other time discretization is the implicit discrete gradient method (McLachlan et al. Reference McLachlan, Quispel and Robidoux1999), which preserves the energy exactly.
Hamiltonian splitting method. We split the Hamiltonian (3.9) as $H = H_1 + H_2$![]() , where
, where

which give the following two corresponding subsystems,
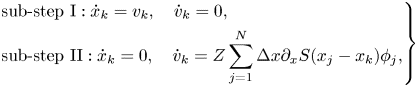
where $\phi _j (j = 1, \ldots, N)$![]() are given by the discrete Poisson–Boltzmann equation (the second equation in (3.5)). Both sub-steps can be solved exactly. Here, we present the first- and second-order methods by the composition method (Hairer et al. Reference Hairer, Lubich and Wanner2006),
are given by the discrete Poisson–Boltzmann equation (the second equation in (3.5)). Both sub-steps can be solved exactly. Here, we present the first- and second-order methods by the composition method (Hairer et al. Reference Hairer, Lubich and Wanner2006),
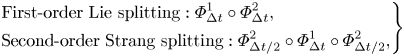
where $\varPhi ^{1}_{\Delta t}$![]() and $\varPhi^2_{\Delta t}$
and $\varPhi^2_{\Delta t}$![]() are solution maps of sub-steps I and II, respectively. Higher order structure-preserving schemes can be constructed by composition methods (Hairer et al. Reference Hairer, Lubich and Wanner2006).
are solution maps of sub-steps I and II, respectively. Higher order structure-preserving schemes can be constructed by composition methods (Hairer et al. Reference Hairer, Lubich and Wanner2006).
Discrete gradient method. We use the second-order discrete gradient method proposed by Gonzalez (Reference Gonzalez1996) to conserve energy exactly,
where
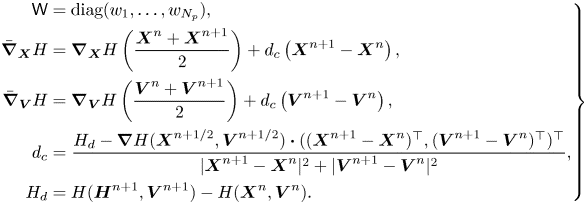
This discrete gradient method is implicit, for which the fixed-point iteration method is used. The degree of shape function $S$![]() is chosen to be at least two for the convergence of iterations.
is chosen to be at least two for the convergence of iterations.
4 Asymptotic limits
In this section, we discuss two asymptotic limits, quasi-neutral limit and large $T_e$![]() limit, with corresponding suitable normalization.
limit, with corresponding suitable normalization.
4.1 Quasi-neutral limit
We do the normalization as

where $x^*$![]() is the space scale of interest, $Z\omega _i = \sqrt {{\bar {n} Z^2 e^2}/{\epsilon _0 m_i}}$
is the space scale of interest, $Z\omega _i = \sqrt {{\bar {n} Z^2 e^2}/{\epsilon _0 m_i}}$![]() is the ion plasma frequency, $\lambda _D = \sqrt {{\epsilon _0 k_B \bar {T}_e}/{\bar {n} e^2}}$
is the ion plasma frequency, $\lambda _D = \sqrt {{\epsilon _0 k_B \bar {T}_e}/{\bar {n} e^2}}$![]() is the electron Debye length, $C_0 = \lambda _D \omega _i = \sqrt {{k_B \bar {T}_e}/{m_i}}$
is the electron Debye length, $C_0 = \lambda _D \omega _i = \sqrt {{k_B \bar {T}_e}/{m_i}}$![]() , $\bar {n}$
, $\bar {n}$![]() is the characteristic ion density and $\bar {T}_e$
is the characteristic ion density and $\bar {T}_e$![]() is the characteristic electron temperature. Then, we get the normalized HBS model (tilde symbol is omitted for convenience)
is the characteristic electron temperature. Then, we get the normalized HBS model (tilde symbol is omitted for convenience)

where $\lambda = \lambda _D / x^*$![]() .
.
When we take the quasi-neutral limit $\lambda \rightarrow 0$![]() for the normalized HBS model (4.2), we get the following hybrid model with quasi-neutrality and Boltzmann electrons (Rambo Reference Rambo1995; Xiao & Qin Reference Xiao and Qin2019a):
for the normalized HBS model (4.2), we get the following hybrid model with quasi-neutrality and Boltzmann electrons (Rambo Reference Rambo1995; Xiao & Qin Reference Xiao and Qin2019a):

By the similar calculations for the Vlasov–Poisson equation as Sonnendrücker (Reference Sonnendrücker2017), we get the dispersion relation of the linear Landau damping of (4.2) with $Z = 1, n_0=1, {\phi _0 = 0}$![]() ,
,
where $\mathcal {Z}$![]() is the plasma dispersion function and $T_i = v^2_T/2$
is the plasma dispersion function and $T_i = v^2_T/2$![]() . By $\lambda \rightarrow 0$
. By $\lambda \rightarrow 0$![]() , we get the dispersion relation of (4.3) (Kunz, Stone & Bai Reference Kunz, Stone and Bai2014),
, we get the dispersion relation of (4.3) (Kunz, Stone & Bai Reference Kunz, Stone and Bai2014),
Under this normalization (4.1a–h), the discrete Poisson–Boltzmann equation in our scheme (3.14) becomes

When taking the quasi-neutral limit for the scheme (3.14) with (4.6), we get the following structure-preserving scheme similar to the scheme proposed by Xiao & Qin (Reference Xiao and Qin2019a) derived using discrete exterior calculus and Whitney form,

where $\phi _j, j = 1, \ldots, N$![]() are determined by the following discrete equation about ${\boldsymbol {\phi }}$
are determined by the following discrete equation about ${\boldsymbol {\phi }}$![]() ,
,

Then the limiting scheme (4.7) is the Hamiltonian splitting method for the quasi-neutral limit model (4.3), i.e. scheme (3.14), and is asymptotic preserving (Jin Reference Jin1999) and structure-preserving at the same time. Similarly, the discrete gradient method (3.16a,b) for the HBS model becomes a discrete gradient method for the hybrid model with quasi-neutrality and Boltzmann electrons. Note that quasi-neutral limit is not a singular asymptotic limit as explained by Degond et al. (Reference Degond, Liu, Savelief and Vignal2012) for the case of the Euler–Poisson–Boltzmann model.
4.2 Large $T_e$ limit
limit
Here, we adopt the normalization (2.3a–h). By taking the $T_e \rightarrow +\infty$![]() in (2.4), we get the equations
in (2.4), we get the equations

Dividing by $k^2T_e$![]() on both sides of the dispersion relation (4.4) of (2.4), we get the the following dispersion relation with the current normalization:
on both sides of the dispersion relation (4.4) of (2.4), we get the the following dispersion relation with the current normalization:
By $T_e \rightarrow +\infty$![]() , we get the dispersion relation of model (4.9) (Sonnendrücker Reference Sonnendrücker2017),
, we get the dispersion relation of model (4.9) (Sonnendrücker Reference Sonnendrücker2017),
Similar to the quasi-neutral limit, when $T_e \rightarrow +\infty$![]() , the limiting schemes of the Hamiltonian splitting method (3.14) and the discrete gradient method (3.16a,b) become the Hamiltonian splitting method and the discrete gradient method for model (4.9).
, the limiting schemes of the Hamiltonian splitting method (3.14) and the discrete gradient method (3.16a,b) become the Hamiltonian splitting method and the discrete gradient method for model (4.9).
5 Electromagnetic hybrid model
Here, we extend the aforementioned structure-preserving methods to an electromagnetic hybrid model with Boltzmann electrons and space charge effects proposed by Vu (Reference Vu1996). This model is derived using a temporal WKB approximation when there is a laser with high frequency $w_0$![]() injected into the plasma, such that numerical simulations on the time scale of the ions can be conducted. We assume the vector potential can be written as
injected into the plasma, such that numerical simulations on the time scale of the ions can be conducted. We assume the vector potential can be written as
where ${\boldsymbol {a}} = (a_1, a_2, a_3)^\top = {\boldsymbol {a}}_r + \mathrm {i}{\boldsymbol {a}}_i$![]() is complex-valued and is assumed to vary on a time scale much longer than $2{\rm \pi} /w_0$
is complex-valued and is assumed to vary on a time scale much longer than $2{\rm \pi} /w_0$![]() , and $*$
, and $*$![]() denotes the conjugate of the complex number. More details of the derivation can be found from Vu (Reference Vu1996). After the following normalization:
denotes the conjugate of the complex number. More details of the derivation can be found from Vu (Reference Vu1996). After the following normalization:

where $c$![]() is the speed of light and $n_c$
is the speed of light and $n_c$![]() is the characteristic density, we have the normalized hybrid model (Vu Reference Vu1996),
is the characteristic density, we have the normalized hybrid model (Vu Reference Vu1996),

where $Z$![]() is the ion charge number, $\epsilon$
is the ion charge number, $\epsilon$![]() is very small due to high frequency $w_0$
is very small due to high frequency $w_0$![]() of the pump wave, and $n_e$
of the pump wave, and $n_e$![]() is determined by the potential $\phi$
is determined by the potential $\phi$![]() and ${\boldsymbol {a}}$
and ${\boldsymbol {a}}$![]() via the following relations with the given functions $n_0$
via the following relations with the given functions $n_0$![]() and $C$
and $C$![]() :
:
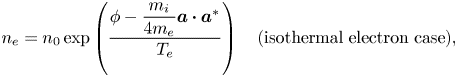

The equation satisfied by ${\boldsymbol {a}}$![]() is a Schrödinger-type equation in the form similar to the semiclassical regime (Bao, Jin & Markowich Reference Bao, Jin and Markowich2002). Although the small parameter $\epsilon$
is a Schrödinger-type equation in the form similar to the semiclassical regime (Bao, Jin & Markowich Reference Bao, Jin and Markowich2002). Although the small parameter $\epsilon$![]() in the Schrödinger equation introduces strong oscillations, the time step size larger than $\epsilon$
in the Schrödinger equation introduces strong oscillations, the time step size larger than $\epsilon$![]() is used by Vu (Reference Vu1996). The commonly used numerical scheme for the Schrödinger equation in the semiclassical regime is the time splitting spectral method (Bao et al. Reference Bao, Jin and Markowich2002), which has the advantage of using large time step sizes and mesh sizes, especially for the computation about the observables, such as the term ${\boldsymbol {a}}\boldsymbol {\cdot }{\boldsymbol {a}}^*$
is used by Vu (Reference Vu1996). The commonly used numerical scheme for the Schrödinger equation in the semiclassical regime is the time splitting spectral method (Bao et al. Reference Bao, Jin and Markowich2002), which has the advantage of using large time step sizes and mesh sizes, especially for the computation about the observables, such as the term ${\boldsymbol {a}}\boldsymbol {\cdot }{\boldsymbol {a}}^*$![]() in this hybrid model.
in this hybrid model.
Regarding the geometric structure, we propose the following Poisson bracket, which is the sum of the Poisson brackets of the HBS model (2.4) and the Schrödinger equation (Marsden & Ratiu Reference Marsden and Ratiu2013) (scaled by $\epsilon$![]() ):
):
The above model (5.3) can be derived with the above Poisson bracket (5.6) and the following Hamiltonian for the isothermal and adiabatic electron cases, respectively:

The phase-space discretization can be conducted as above through the discretization of the Poisson bracket as done by Qin et al. (Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2015b) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017) or by Fourier particle methods (Campos Pinto et al. Reference Campos Pinto, Ameres, Kormann and Sonnendrücker2024). The Hamiltonian splitting method (Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015; Qin et al. Reference Qin, He, Zhang, Liu, Xiao and Wang2015a; He et al. Reference He, Qin, Sun, Xiao, Zhang and Liu2015) gives three explicitly solvable subsystems (or in Fourier space), further details are presented in Appendix B.
6 Numerical experiments
In this section, three numerical experiments: finite grid instability (of an equilibrium), Landau damping (of damping waves) and resonantly excited nolinear ion waves (with non-zero $\phi _0$![]() ), are conducted using the normalization (2.3a–h) to illustrate the conservation properties of the schemes (3.14)–(3.16a,b) of the HBS model (2.4). The reference density $n_0$
), are conducted using the normalization (2.3a–h) to illustrate the conservation properties of the schemes (3.14)–(3.16a,b) of the HBS model (2.4). The reference density $n_0$![]() is set to 1 and the unit charge number $Z = 1$
is set to 1 and the unit charge number $Z = 1$![]() . The degree of the shape function is 2, the tolerance for the fixed point iteration is $10^{-12}$
. The degree of the shape function is 2, the tolerance for the fixed point iteration is $10^{-12}$![]() and periodic boundary conditions are used.
and periodic boundary conditions are used.
6.1 Finite grid instability
Finite grid instability in the context of hybrid simulations was first reported by Rambo (Reference Rambo1995) for the hybrid model with quasi-neutrality and Boltzmann electrons. This numerical phenomenon typically arises in standard particle-in-cell methods when the temperature ratio $T_e/T_i \gg 1$![]() , and ions are heated until the ion thermal speed becomes comparable to the ion acoustic speed (and therefore, $T_e/T_i \approx 1$
, and ions are heated until the ion thermal speed becomes comparable to the ion acoustic speed (and therefore, $T_e/T_i \approx 1$![]() ). Rambo (Reference Rambo1997) noted that finite grid instability also occurs when using traditional particle-in-cell methods for the HBS model, although it is weaker than the hybrid model with quasi-neutrality and Boltzmann electrons. Stanier, Chacón & Chen (Reference Stanier, Chacón and Chen2019) and Li et al. (Reference Li, Campos-Pinto, Holderied, Possanner and Sonnendrücker2024a,Reference Li, Holderied, Possanner and Sonnendrückerb) numerically reduced the finite grid instability by using the conservative or bracket-based particle-in-cell methods for the hybrid model with quasi-neutrality and massless electrons. The finite grid instability of particle-in-cell methods has also been studied by Huang et al. (Reference Huang, Zeng, Wang, Meyers, Yi and Albright2016) and Xiao & Qin (Reference Xiao and Qin2019b), which reveals that the aliased spatial modes are the major cause of the finite grid instability in the particle-in-cell methods, and geometric particle-in-cell methods are able to suppress the finite grid instability.
). Rambo (Reference Rambo1997) noted that finite grid instability also occurs when using traditional particle-in-cell methods for the HBS model, although it is weaker than the hybrid model with quasi-neutrality and Boltzmann electrons. Stanier, Chacón & Chen (Reference Stanier, Chacón and Chen2019) and Li et al. (Reference Li, Campos-Pinto, Holderied, Possanner and Sonnendrücker2024a,Reference Li, Holderied, Possanner and Sonnendrückerb) numerically reduced the finite grid instability by using the conservative or bracket-based particle-in-cell methods for the hybrid model with quasi-neutrality and massless electrons. The finite grid instability of particle-in-cell methods has also been studied by Huang et al. (Reference Huang, Zeng, Wang, Meyers, Yi and Albright2016) and Xiao & Qin (Reference Xiao and Qin2019b), which reveals that the aliased spatial modes are the major cause of the finite grid instability in the particle-in-cell methods, and geometric particle-in-cell methods are able to suppress the finite grid instability.
In this test, we investigate the finite grid instability using the following initial condition (an equilibrium of (2.4)) by the numerical simulations conducted with schemes (3.14) and (3.16a,b),
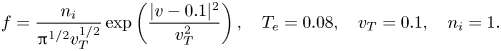
Computational parameters include: domain $[0, 5{\rm \pi} ]$![]() , time step size $\Delta t = 0.05$
, time step size $\Delta t = 0.05$![]() and particle number per cell $100$
and particle number per cell $100$![]() . We run the simulations with the numerical methods (3.14) and (3.16a,b) with different cell sizes, i.e. $\Delta x = 5{\rm \pi} /12, 5{\rm \pi} /25, 5{\rm \pi} /50, 5{\rm \pi} /100$
. We run the simulations with the numerical methods (3.14) and (3.16a,b) with different cell sizes, i.e. $\Delta x = 5{\rm \pi} /12, 5{\rm \pi} /25, 5{\rm \pi} /50, 5{\rm \pi} /100$![]() , and the results are presented in figures 1 and 2. We can see $k(t)/k(0)$
, and the results are presented in figures 1 and 2. We can see $k(t)/k(0)$![]() ($k(t) = \tfrac {1}{2} \sum _{k=1}^{N_p} w_k v_k^2$
($k(t) = \tfrac {1}{2} \sum _{k=1}^{N_p} w_k v_k^2$![]() the ion kinetic energy) oscillates with time without exhibiting rapid linear growth, as observed in figure 3(a) of Rambo (Reference Rambo1997). This indicates that the finite grid instability is reduced numerically. As the cell size decreases and the electron Debye length is resolved with higher resolution, the oscillating level of $k(t)/k(0)$
the ion kinetic energy) oscillates with time without exhibiting rapid linear growth, as observed in figure 3(a) of Rambo (Reference Rambo1997). This indicates that the finite grid instability is reduced numerically. As the cell size decreases and the electron Debye length is resolved with higher resolution, the oscillating level of $k(t)/k(0)$![]() becomes closer to 1 and the momentum error also becomes smaller. The momentum error also depends on the particle number. When there are 100 cells and 2000 particles in each, the Hamiltonian splitting method with quadratic weighting gives the momentum error at the level of $10^{-4}$
becomes closer to 1 and the momentum error also becomes smaller. The momentum error also depends on the particle number. When there are 100 cells and 2000 particles in each, the Hamiltonian splitting method with quadratic weighting gives the momentum error at the level of $10^{-4}$![]() .
.

Figure 1. Finite grid instability of the HBS model by Hamiltonian splitting method. Time evolution of $k(t)/k(0)$![]() with $k$
with $k$![]() denoting the ion kinetic energy, relative energy error and momentum error.
denoting the ion kinetic energy, relative energy error and momentum error.
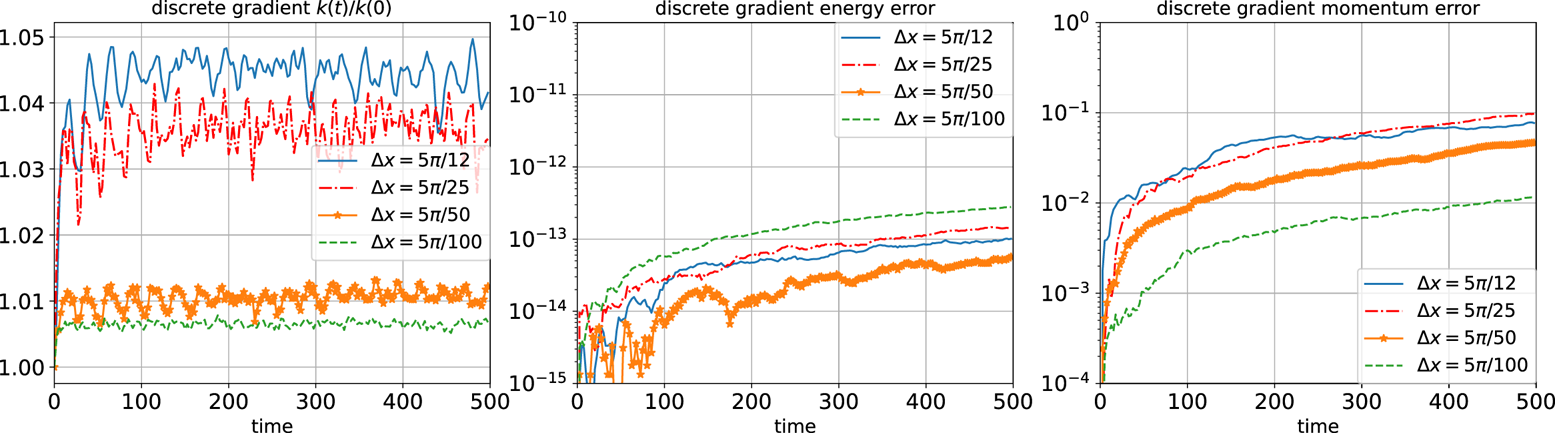
Figure 2. Finite grid instability of the HBS model by discrete gradient method with quadratic weighting. Time evolution of $k(t)/k(0)$![]() with $k$
with $k$![]() denoting the ion kinetic energy, relative energy error and momentum error.
denoting the ion kinetic energy, relative energy error and momentum error.
As the derivatives of B-splines appear in the schemes (3.14) and (3.16a,b), second-order at least B-spline shape functions should be used. As the Hamiltonian splitting method (3.14) (Strang splitting) is symplectic, it has superior long-time numerical behaviour, although energy is not conserved exactly (with a relative error of approximately $10^{-5}$![]() ) with quadratic weighting. In figure 1, the relative energy error is also very small ($10^{-4}$
) with quadratic weighting. In figure 1, the relative energy error is also very small ($10^{-4}$![]() ) even when the first order B-spine is used (the derivative of the B-spine is taken as its right derivative). Relative energy error of the discrete gradient method with quadratic weighting is approximately $10^{-13}$
) even when the first order B-spine is used (the derivative of the B-spine is taken as its right derivative). Relative energy error of the discrete gradient method with quadratic weighting is approximately $10^{-13}$![]() .
.
Here, we discuss the time step size of the Hamiltonian splitting methods. We consider the case with 100 cells in space, time interval $[0,500]$![]() and quadratic weighting. To achieve satisfying results, when $n_i =1$
and quadratic weighting. To achieve satisfying results, when $n_i =1$![]() and the number of particles per cell is 100, the maximum time step size is 0.5 approximately with energy error at the level of $10^{-4}$
and the number of particles per cell is 100, the maximum time step size is 0.5 approximately with energy error at the level of $10^{-4}$![]() . For higher initial densities, such as $n_i = 4, 16$
. For higher initial densities, such as $n_i = 4, 16$![]() with $400, 1600$
with $400, 1600$![]() particles per cell, the maximum time step sizes giving satisfying results are approximately $0.3,0.3$
particles per cell, the maximum time step sizes giving satisfying results are approximately $0.3,0.3$![]() with energy errors at the level of $10^{-4}, 10^{-4}$
with energy errors at the level of $10^{-4}, 10^{-4}$![]() , respectively.
, respectively.
6.2 Landau damping
First, we simulate the linear ion Landau damping by one-dimensional simulations. The initial distribution function is

The computational parameters are as follows: grid number 64, domain size $[0, 8{\rm \pi} ]$![]() , time step size $\Delta t = 0.05$
, time step size $\Delta t = 0.05$![]() , final computation time $20$
, final computation time $20$![]() , $v_T = 1.4142$
, $v_T = 1.4142$![]() , $n_i = 1$
, $n_i = 1$![]() and total particle number $10^7$
and total particle number $10^7$![]() . In this test, the quadratic weighting is used. See the numerical results with $T_e=5$
. In this test, the quadratic weighting is used. See the numerical results with $T_e=5$![]() in figure 3 by the Hamiltonian splitting method (3.14) and discrete gradient method (3.16a,b). Solving the dispersion relation mentioned in § 4, $1 + {k^2 T_e} = ({T_e}/{T_i}) \mathcal {Z}'({\omega }/{kv_T} ),$
in figure 3 by the Hamiltonian splitting method (3.14) and discrete gradient method (3.16a,b). Solving the dispersion relation mentioned in § 4, $1 + {k^2 T_e} = ({T_e}/{T_i}) \mathcal {Z}'({\omega }/{kv_T} ),$![]() we find $\omega = 0.6986 - 0.0810\textrm {i}$
we find $\omega = 0.6986 - 0.0810\textrm {i}$![]() when $k = 0.25$
when $k = 0.25$![]() . Methods (3.14)–(3.16a,b) give an accurate damping rate of the electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$
. Methods (3.14)–(3.16a,b) give an accurate damping rate of the electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$![]() . The dispersion relation $1 = ({T_e}/{T_i}) \mathcal {Z}'({\omega }/{kv_T} )$
. The dispersion relation $1 = ({T_e}/{T_i}) \mathcal {Z}'({\omega }/{kv_T} )$![]() of the model with quasi-neutrality and Boltzmann electrons (Xiao & Qin Reference Xiao and Qin2019a) in § 4 yields $\omega = 0.7528 - 0.05806\textrm {i}$
of the model with quasi-neutrality and Boltzmann electrons (Xiao & Qin Reference Xiao and Qin2019a) in § 4 yields $\omega = 0.7528 - 0.05806\textrm {i}$![]() , i.e. a slower damping rate. The energy errors of the schemes (3.14)–(3.16a,b) are approximately $10^{-4}$
, i.e. a slower damping rate. The energy errors of the schemes (3.14)–(3.16a,b) are approximately $10^{-4}$![]() and $10^{-13}$
and $10^{-13}$![]() , respectively.
, respectively.
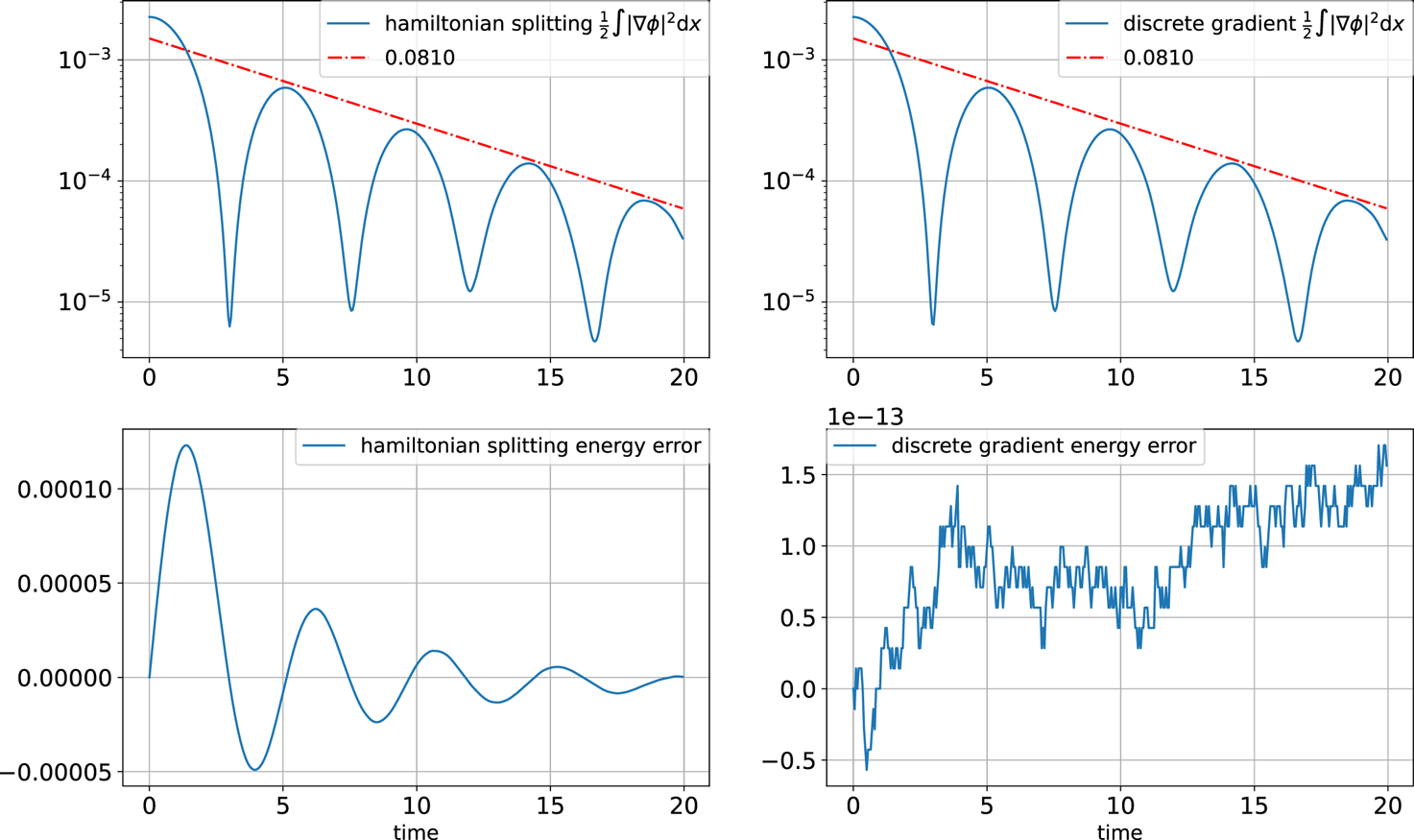
Figure 3. Linear Landau damping of the HBS model with $T_e=5$![]() by Hamiltonian splitting and discrete gradient methods. Time evolution of the electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$
by Hamiltonian splitting and discrete gradient methods. Time evolution of the electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$![]() and total energy error.
and total energy error.
Then, we simulate nonlinear ion Landau damping. The initial distribution function is

The computational parameters are as follows: grid number 65, domain size $[0, 4{\rm \pi} ]$![]() , time step size $\Delta t = 0.05$
, time step size $\Delta t = 0.05$![]() , final computation time $40$
, final computation time $40$![]() , $v_T = 1.4142, n_i = 1$
, $v_T = 1.4142, n_i = 1$![]() and total particle number $10^5$
and total particle number $10^5$![]() . In this test, the quadratic weighting is used. See the numerical results with large $T_e=100$
. In this test, the quadratic weighting is used. See the numerical results with large $T_e=100$![]() in figure 4 by the Hamiltonian splitting method (3.14) and discrete gradient method (3.16a,b). Due to the large $T_e$
in figure 4 by the Hamiltonian splitting method (3.14) and discrete gradient method (3.16a,b). Due to the large $T_e$![]() , the term $\exp (\phi /T_e)$
, the term $\exp (\phi /T_e)$![]() approximates 1, making the solution of the HBS model (2.4) approximate the solution of the Vlasov–Poisson system (with static electron density as 1). In figure 4, we observe the nonlinear Landau damping. The time evolution of energy component $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d}{x}$
approximates 1, making the solution of the HBS model (2.4) approximate the solution of the Vlasov–Poisson system (with static electron density as 1). In figure 4, we observe the nonlinear Landau damping. The time evolution of energy component $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d}{x}$![]() decays exponentially initially, and the decay rate is very close to the decay rate 0.2854 of the Vlasov–Poisson system (Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017) before time $T=10$
decays exponentially initially, and the decay rate is very close to the decay rate 0.2854 of the Vlasov–Poisson system (Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017) before time $T=10$![]() . Here, $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d}{x}$
. Here, $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d}{x}$![]() oscillates when $t \in [10, 30]$
oscillates when $t \in [10, 30]$![]() , then grows exponentially with time when $t \in [30, 40]$
, then grows exponentially with time when $t \in [30, 40]$![]() with a rate close to 0.086671 (Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017) of the Vlasov–Poisson system. For the Hamiltonian splitting method, the energy error is approximately $10^{-2}$
with a rate close to 0.086671 (Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017) of the Vlasov–Poisson system. For the Hamiltonian splitting method, the energy error is approximately $10^{-2}$![]() . The discrete gradient method gives a smaller total energy error of approximately $10^{-12}$
. The discrete gradient method gives a smaller total energy error of approximately $10^{-12}$![]() , and a similar behaviour of the electric energy is presented. The errors of neutrality given by both numerical methods are at the level of iteration tolerance. For the time step size of the Hamiltonian splitting methods, we consider the case with 65 cells in space, time interval $[0,40]$
, and a similar behaviour of the electric energy is presented. The errors of neutrality given by both numerical methods are at the level of iteration tolerance. For the time step size of the Hamiltonian splitting methods, we consider the case with 65 cells in space, time interval $[0,40]$![]() , $10^5$
, $10^5$![]() particles and quadratic weighting. As $T_e=100$
particles and quadratic weighting. As $T_e=100$![]() is large, $\exp (\phi /T_e)$
is large, $\exp (\phi /T_e)$![]() is close to 1, the numerical stability property is close to the result of Kormann & Sonnendrücker (Reference Kormann and Sonnendrücker2021), i.e. the stability condition is approximately $\Delta t \omega _i < 2$
is close to 1, the numerical stability property is close to the result of Kormann & Sonnendrücker (Reference Kormann and Sonnendrücker2021), i.e. the stability condition is approximately $\Delta t \omega _i < 2$![]() . To get the acceptable accuracy, the time step size is usually chosen smaller than 2. When $n_i = 1$
. To get the acceptable accuracy, the time step size is usually chosen smaller than 2. When $n_i = 1$![]() , the maximum time step size yielding good numerical behaviour is $\Delta t = 0.4$
, the maximum time step size yielding good numerical behaviour is $\Delta t = 0.4$![]() , resulting in an energy error of approximately $0.45$
, resulting in an energy error of approximately $0.45$![]() after saturation; for $n_i = 4$
after saturation; for $n_i = 4$![]() , $\Delta t = 0.2$
, $\Delta t = 0.2$![]() gives an energy error of approximately $0.4$
gives an energy error of approximately $0.4$![]() after saturation, and for $n_i = 16$
after saturation, and for $n_i = 16$![]() , $\Delta t = 0.12$
, $\Delta t = 0.12$![]() results in an energy error of approximately $0.3$
results in an energy error of approximately $0.3$![]() after saturation. We also consider the case with a small electron temperature $T_e = 1$
after saturation. We also consider the case with a small electron temperature $T_e = 1$![]() . In this case, when $n_i = 1$
. In this case, when $n_i = 1$![]() , $\Delta t = 0.5$
, $\Delta t = 0.5$![]() gives an energy error of approximately 0.05 after saturation; when $n_i = 4$
gives an energy error of approximately 0.05 after saturation; when $n_i = 4$![]() , $\Delta t = 0.2$
, $\Delta t = 0.2$![]() gives an energy error of approximately 0.002 after saturation; when $n_i = 16$
gives an energy error of approximately 0.002 after saturation; when $n_i = 16$![]() , $\Delta t = 0.1$
, $\Delta t = 0.1$![]() gives an energy error of approximately 0.004.
gives an energy error of approximately 0.004.

Figure 4. Nonlinear Landau damping of the HBS model with $T_e=100$![]() by Hamiltonian splitting and discrete gradient methods. Time evolution of total energy error and electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$
by Hamiltonian splitting and discrete gradient methods. Time evolution of total energy error and electric energy $\tfrac {1}{2}\int |\boldsymbol {\nabla } \phi |^2 \,\mathrm {d} x$![]() .
.
6.3 Simulations with the ponderomotive driving term
Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997) numerically solved the HBS model with a ponderomotive driving term to study nonlinear ion acoustic waves. Here, following Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997), we conduct a simulation with a non-zero given time-dependent function $\phi _0$![]() in (2.4). Specifically, the initial condition and $\phi _0$
in (2.4). Specifically, the initial condition and $\phi _0$![]() are given by
are given by

where $n_i = 1, v_T = \tfrac {\sqrt {2}}{10}$![]() , $\tilde {\phi }_0 = 0.05T_e$
, $\tilde {\phi }_0 = 0.05T_e$![]() , $\varOmega = 0.4472$
, $\varOmega = 0.4472$![]() , $k = 1.49$
, $k = 1.49$![]() . Other computational parameters are: grid number 64, domain size $[0, {10{\rm \pi} }/{k}]$
. Other computational parameters are: grid number 64, domain size $[0, {10{\rm \pi} }/{k}]$![]() , time step size $\Delta t = 0.1$
, time step size $\Delta t = 0.1$![]() , final computation time $600$
, final computation time $600$![]() , $T_e = 0.1125$
, $T_e = 0.1125$![]() and total particle number $10^6$
and total particle number $10^6$![]() . In this test, the quadratic weighting is used. Since $\phi _0$
. In this test, the quadratic weighting is used. Since $\phi _0$![]() is time dependent, the Hamiltonian system (3.10) is a non-autonomous Hamiltonian system, for which we use the the technique of extending the dimension (Zhou et al. Reference Zhou, He, Sun, Liu and Qin2017). From figures 5 and 6, we can see that the peak value of the response function $R(t) = \max _{x}({\phi }/{\phi _0})$
is time dependent, the Hamiltonian system (3.10) is a non-autonomous Hamiltonian system, for which we use the the technique of extending the dimension (Zhou et al. Reference Zhou, He, Sun, Liu and Qin2017). From figures 5 and 6, we can see that the peak value of the response function $R(t) = \max _{x}({\phi }/{\phi _0})$![]() is approximately 5, which is consistent with the result of Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997). There are a rapid oscillation at $2.1\varOmega$
is approximately 5, which is consistent with the result of Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997). There are a rapid oscillation at $2.1\varOmega$![]() and a slow modulation at $0.04\varOmega$
and a slow modulation at $0.04\varOmega$![]() in the fourth figure obtained by the fast Fourier transformation of $\max _x({\phi }/{\phi _0})$
in the fourth figure obtained by the fast Fourier transformation of $\max _x({\phi }/{\phi _0})$![]() in time, which are close to the results of Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997) with $1.85 \varOmega$
in time, which are close to the results of Cohen et al. (Reference Cohen, Lasinski, Langdon and Williams1997) with $1.85 \varOmega$![]() (fast) and $0.15\varOmega$
(fast) and $0.15\varOmega$![]() (slow). The Hamiltonian splitting method and discrete gradient method give the energy errors of approximately $10^{-5}$
(slow). The Hamiltonian splitting method and discrete gradient method give the energy errors of approximately $10^{-5}$![]() and $10^{-12}$
and $10^{-12}$![]() , respectively. Additionally, when $t=400$
, respectively. Additionally, when $t=400$![]() , both methods give similar five vortices in phase-space contour plots, due to the driving force being the fifth mode, i.e. $k = 5 ({2{\rm \pi} }/{L})$
, both methods give similar five vortices in phase-space contour plots, due to the driving force being the fifth mode, i.e. $k = 5 ({2{\rm \pi} }/{L})$![]() , where $L$
, where $L$![]() is the domain size.
is the domain size.

Figure 5. Simulations with the ponderomotive driving term by Hamiltonian splitting method. Time evolutions of $R(t) = \max ({\phi }/{\tilde {\phi }_0})$![]() and energy error, the contour plot of the distribution function at time $t=400$
and energy error, the contour plot of the distribution function at time $t=400$![]() , and the fast Fourier transformation of $R(t)$
, and the fast Fourier transformation of $R(t)$![]() .
.

Figure 6. Simulations with the ponderomotive driving term by discrete gradient method. Time evolutions of $R(t) = \max ({\phi }/{\tilde {\phi }_0})$![]() and energy error, the contour plot of the distribution function at time $t=400$
and energy error, the contour plot of the distribution function at time $t=400$![]() , and the fast Fourier transformation of $R(t)$
, and the fast Fourier transformation of $R(t)$![]() .
.
Regarding the time step size for the Hamiltonian splitting methods, we use the same parameters as above but vary the initial density and time step size. When the initial density $n_i = 1$![]() , the maximum step size for giving good numerical behaviour is $\Delta t = 1.5$
, the maximum step size for giving good numerical behaviour is $\Delta t = 1.5$![]() , which gives an energy error of approximately 0.003; When the initial density $n_i = 4$
, which gives an energy error of approximately 0.003; When the initial density $n_i = 4$![]() , the maximum step size $\Delta t = 1$
, the maximum step size $\Delta t = 1$![]() gives an energy error of approximately 0.02; when the initial density $n_i = 16$
gives an energy error of approximately 0.02; when the initial density $n_i = 16$![]() , the maximum step size $\Delta t = 0.5$
, the maximum step size $\Delta t = 0.5$![]() gives an energy error of approximately 0.008.
gives an energy error of approximately 0.008.
7 Conclusion
In this paper, we explore the structure-preserving discretizations of the electrostatic hybrid plasma model with Boltzmann electrons and space-charge effects. These discretizations are derived by discretizing either the variational action integral or the Poisson bracket combined with the Hamiltonian splitting methods (Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015; He et al. Reference He, Qin, Sun, Xiao, Zhang and Liu2015; Qin et al. Reference Qin, He, Zhang, Liu, Xiao and Wang2015a) in time. Discrete gradient methods (McLachlan et al. Reference McLachlan, Quispel and Robidoux1999) are employed to conserve energy exactly. The geometric structure and numerical discretization of the electromagnetic hybrid model (Vu Reference Vu1996) are detailed in § 5.
For discretizing the field functions, the finite element methods (Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017) or Fourier spectral methods (Campos Pinto et al. Reference Campos Pinto, Ameres, Kormann and Sonnendrücker2024) can be used, while the distribution function can be discretized by the delta functions. Additional details can be found in Appendix A. The cases with other kinds of boundary conditions and further exploration (such as the physical application and the time and mesh size strategy) of the electromagnetic hybrid model can be considered in future works.
Acknowledgements
The simulations in this work were performed at the Max Planck Computing & Data Facility (MPCDF). The author would like to thank the anonymous reviewers for many helpful comments for improving this paper. Special thanks to B.I. Cohen for the help of the simulation parameters used in § 6.3. The author would like to acknowledge P.J. Morrison, S. Possanner and E. Sonnendrücker for their kind discussions of this work.
Editor L.O. Silva thanks the referees for their advice in evaluating this article.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Discretization with finite element method
Distribution function $f$![]() is approximated using $\delta$
is approximated using $\delta$![]() functions, i.e.
functions, i.e.

where $N_p$![]() is the total particle number, and $w_k$
is the total particle number, and $w_k$![]() , ${x}_k$
, ${x}_k$![]() , and ${v}_k$
, and ${v}_k$![]() are the weight, position and velocity for the $k$
are the weight, position and velocity for the $k$![]() th particle. We discretize $\phi$
th particle. We discretize $\phi$![]() by the finite element method, i.e.
by the finite element method, i.e.
where the vectors ${\boldsymbol {\varLambda }}$![]() and ${\boldsymbol {\phi }}$
and ${\boldsymbol {\phi }}$![]() contain all basis functions and finite element coefficients. The Poisson–Boltzmann equation is discretized in a weak formulation as
contain all basis functions and finite element coefficients. The Poisson–Boltzmann equation is discretized in a weak formulation as

where ${x}_j$![]() is the $j$
is the $j$![]() th quadrature point, and $w_j$
th quadrature point, and $w_j$![]() is the corresponding quadrature weight. We define a matrix $\boldsymbol{\mathsf{M}}, \text{with}\,\mathsf{M}_{ij} = \int \partial _x \varLambda _i \partial _x \varLambda _j \,\mathrm {d}{x}$
is the corresponding quadrature weight. We define a matrix $\boldsymbol{\mathsf{M}}, \text{with}\,\mathsf{M}_{ij} = \int \partial _x \varLambda _i \partial _x \varLambda _j \,\mathrm {d}{x}$![]() .
.
We approximate variational action integral (2.6) as

Hamiltonian is discretized as
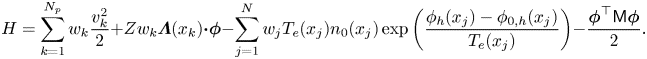
As done by Qin et al. (Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2015b) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017), the bracket is discretized as
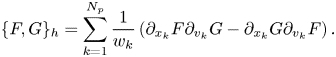
Both the variations of (A4) and the discrete Poisson bracket (A6) with Hamiltonian (A6) give the following Hamiltonian ordinary differential equation:
Similarly, for the cases with periodic boundary conditions, we can prove that the neutrality condition holds in a weak sense, i.e.

Appendix B. Hamiltonian splitting method for the electromagnetic hybrid model (Vu Reference Vu1996)
We take the isothermal electron case with the following energy for an example:

We split the Hamiltonian into the following three parts and get the corresponding explicitly solvable subsystems,

Subsystem $H_{1}$![]() . The corresponding subsystem is
. The corresponding subsystem is
where the first equation is an explicitly solvable transport equation and the second equation can be solved explicitly in Fourier space.
Subsystem $H_{2}$![]() . The corresponding subsystem is
. The corresponding subsystem is
where the ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$![]() is preserved by the second equation and $\int f\,\mathrm {d}{\boldsymbol {v}}$
is preserved by the second equation and $\int f\,\mathrm {d}{\boldsymbol {v}}$![]() is preserved by the first equation, which make the two equations explicitly solvable.
is preserved by the first equation, which make the two equations explicitly solvable.
Subsystem $H_{3}$![]() . The corresponding subsystem is
. The corresponding subsystem is
where ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$![]() is preserved by the second equation and the ion density $\int f\, \mathrm {d}{\boldsymbol {v}}$
is preserved by the second equation and the ion density $\int f\, \mathrm {d}{\boldsymbol {v}}$![]() is preserved by the first equation. As $n_e$
is preserved by the first equation. As $n_e$![]() depends on $\phi$
depends on $\phi$![]() and ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$
and ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$![]() , and ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$
, and ${\boldsymbol {a}} \boldsymbol {\cdot } {\boldsymbol {a}}^*$![]() and $\int f\, \mathrm {d}{\boldsymbol {v}}$
and $\int f\, \mathrm {d}{\boldsymbol {v}}$![]() are not changed in this sub-system, $\phi$
are not changed in this sub-system, $\phi$![]() and $n_e$
and $n_e$![]() are preserved by this subsystem. We only need to solve the third equation for obtaining $\phi$
are preserved by this subsystem. We only need to solve the third equation for obtaining $\phi$![]() once in each time step, and the first and second equations are explicitly solvable.
once in each time step, and the first and second equations are explicitly solvable.























