Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T01:34:48.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Sub-Alfvénic reduced magnetohydrodynamic equations for tokamaks

Part of: Focus on Fusion

Published online by Cambridge University Press:  27 June 2017

W. Sengupta Open the ORCID record for W. Sengupta [Opens in a new window] ,
A. B. Hassam  and
T. M. Antonsen Jr
W. Sengupta*
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD, USA
A. B. Hassam
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD, USA
T. M. Antonsen Jr
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A reduced set of magnetohydrodynamic (MHD) equations is derived, applicable to large aspect ratio tokamaks and relevant for dynamics that is sub-Alfvénic with respect to ideal ballooning modes. This ordering optimally allows sound waves, Mercier modes, drift modes, geodesic-acoustic modes (GAM), zonal flows and shear Alfvén waves. Wavelengths long compared to the gyroradius but comparable to the minor radius of a typical tokamak are considered. With the inclusion of resistivity, tearing modes, resistive ballooning modes, Pfirsch–Schluter cells and the Stringer spin-up are also included. A major advantage is that the resulting system is two-dimensional in space, and the system incorporates self-consistent and dynamic Shafranov shifts. A limitation is that the system is valid only in radial domains where the tokamak safety factor, 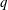$q$, is close to rational. In the tokamak core, the system is well suited to study the sawtooth discharge in the presence of Mercier modes. The systematic ordering scheme and methodology developed are versatile enough to reduce the more general collisional two-fluid equations or possibly the Vlasov–Maxwell system in the MHD ordering.

Keywords

plasma confinementplasma dynamicsplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 3 , June 2017 , 905830307
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Connor, J. W., Hastie, R. J. & Taylor, J. B. 2004 Stability of toroidal plasmas: the influence of magnetic shear, periodicity and rotation. Plasma Phys. Control. Fusion 46 (12B), B1.Google Scholar
Connor, J. W. & Taylor, J. B. 1987 Ballooning modes or fourier modes in a toroidal plasma? Phys. Fluids 30 (10), 3180–3185.Google Scholar
Drake, J. F. & Antonsen, T. M. Jr. 1984 Nonlinear reduced fluid equations for toroidal plasmas. Phys. Fluids 27 (4), 898–908.Google Scholar
Hassam, A. B. 1996 Poloidal rotation of tokamak plasmas at super poloidal sonic speeds. Nucl. Fusion 36 (6), 707.Google Scholar
Hassam, A. B. & Drake, J. F. 1993 Spontaneous poloidal spin-up of tokamak plasmas: reduced equations, physical mechanism, and sonic regimes. Phys. Fluids B 5 (11), 4022–4029.Google Scholar
Hassam, A. B. & Kulsrud, R. M. 1978 Time evolution of mass flows in a collisional tokamak. Phys. Fluids 21 (12), 2271–2279.Google Scholar
Hastie, R. J. & Taylor, J. B. 1981 Validity of ballooning representation and mode number dependence of stability. Nucl. Fusion 21 (2), 187.Google Scholar
Hazeltine, R. D., Kotschenreuther, M. & Morrison, P. J. 1985 A four-field model for tokamak plasma dynamics. Phys. Fluids 28 (8), 2466–2477.Google Scholar
Hazeltine, R. D. & Meiss, J. D. 1985 Shear-alfvén dynamics of toroidally confined plasmas. Phys. Rep. 121 (1–2), 1–164.Google Scholar
Izzo, R., Monticello, D. A., Park, W., Manickam, J., Strauss, H. R., Grimm, R. & McGuire, K. 1983 Effects of toroidicity on resistive tearing modes. Phys. Fluids 26 (8), 2240–2246.Google Scholar
Manickam, J., Pomphrey, N. & Todd, A. M. M. 1987 Ideal MHD stability properties of pressure driven modes in low shear tokamaks. Nucl. Fusion 27 (9), 1461.Google Scholar
Ramos, J. J. 1988 Theory of global interchange modes in shaped tokamaks with small central shear. Phys. Rev. Lett. 60 (6), 523.Google Scholar
Schmalz, R. 1981 Reduced, three-dimensional, nonlinear equations for high- $\unicode[STIX]{x1D6FD}$ plasmas including toroidal effects. Phys. Lett. A 82 (1), 14–17.Google Scholar
Strauss, H. R. 1977 Dynamics of high $\unicode[STIX]{x1D6FD}$ tokamaks. Phys. Fluids 20 (8), 1354–1360.Google Scholar
Strauss, H. R. 1983 Finite-aspect-ratio MHD equations for tokamaks. Nucl. Fusion 23 (5), 649.Google Scholar
Strauss, H. R. 1976 Nonlinear, three-dimensional magnetohydrodynamics of noncircular tokamaks. Phys. Fluids 19 (1), 134–140.Google Scholar
Stringer, T. E. 1969 Diffusion in toroidal plasmas with radial electric field. Phys. Rev. Lett. 22 (15), 770.Google Scholar
Waelbroeck, F. L. 2011 Models for sub-alfvénic magnetodynamics of fusion plasmas. Fusion Sci. Technol. 59 (3), 499–518.CrossRefGoogle Scholar
White, R., Monticello, D., Rosenbluth, M. N., Strauss, H. & Kadomtsev, B. B. 1974 Numerical studies of nonlinear evolution of kink and tearing modes in tokamaks. In International Conference of Plasma Physics, Tokyo, pp. 495–504.Google Scholar