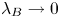Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T23:50:30.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Study of the electron–atom collisions in dense semiclassical plasma of noble gases

Published online by Cambridge University Press:  01 March 2022

Karlygash N. Dzhumagulova ,
Erik O. Shalenov Open the ORCID record for Erik O. Shalenov [Opens in a new window] ,
Yerkhan A. Tashkenbayev  and
Tlekkabyl S. Ramazanov
Karlygash N. Dzhumagulova
Affiliation:
Institute of Experimental and Theoretical Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Plasma Physics, Nanotechnology and Computer Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Physics, Nazarbayev University, Nur-Sultan 010000, Kazakhstan
Erik O. Shalenov*
Affiliation:
Institute of Experimental and Theoretical Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Plasma Physics, Nanotechnology and Computer Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Physics, Nazarbayev University, Nur-Sultan 010000, Kazakhstan
Yerkhan A. Tashkenbayev
Affiliation:
Institute of Experimental and Theoretical Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Plasma Physics, Nanotechnology and Computer Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan
Tlekkabyl S. Ramazanov
Affiliation:
Institute of Experimental and Theoretical Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan Department of Plasma Physics, Nanotechnology and Computer Physics, al-Farabi Kazakh National University, Almaty 050040, Kazakhstan
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

We present the effective optical potential of the interaction of an electron with an atom in dense semiclassical plasma of noble gases. This potential takes into account the collective screening effect and the quantum mechanical effect of diffraction. The influence of diffraction and screening effects on the characteristics of electron–atom collisions was investigated. Scattering phase shifts decrease with increase of the de Broglie wave. The electron–atom momentum-transfer cross-section at $\lambda _{B}\to 0$ tends to the data obtained earlier with a neglecting of the diffraction effect.

Keywords

plasma simulationstrongly coupled plasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 905880119
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

1. Introduction

The study of electron scattering by noble gas atoms has always been a hot topic. Suffice it to recall that the discovery of the Ramsauer–Townsend effect (Ramsauer Reference Ramsauer1921; Townsend & Bailey Reference Townsend and Bailey1922) at one time caused great amazement by its unexpectedness and incomprehensible origin, but which was later explained as a consequence of the effect of diffraction of de Broglie waves using the theory of quantum mechanics, which was making its first successes at that time. Currently, these studies have not lost their relevance both in experimental research and in theoretical study. Most of the experimental measurements of the scattering cross-sections refer to the region of intermediate scattering angles, approximately from ${10^\circ }$ to ${150^\circ }$. At smaller and larger angles, the existing experimental data are often qualitative assessments, and here their greatest deviation from theoretical estimates is observed. In this regard, the implementation of accurate measurements in the regions of small and large scattering angles is still a big challenge in the problem of obtaining reliable experimental scattering cross-sections over the entire range of scattering angles (Adibzadeh & Theodosiou Reference Adibzadeh and Theodosiou2005; Cho et al. Reference Cho, McEachran, Buckman and Tanaka2008). Moreover, this problem is especially relevant for heavier atoms of noble gases.

Recently, in a number of experimental works devoted to the investigation of the properties of partially ionized plasma of noble gases, unexpected effects have been noted, associated, as it turned out later, with electron–atom interactions in the system. For example, in Kuhlbrodt et al. (Reference Kuhlbrodt, Redmer, Reinholz, Röpke, Holst, Mintsev, Gryaznov, Shilkin and Fortov2005) it was shown that the presence of the temperature-dependent minimum on the direct current conductivity of noble gases and this minimum has been explained by electron–atom collisions (see Adams et al. (Reference Adams, Reinholz, Redmer, Mintsev, Shilkin and Gryaznov2007) and Rosmej, Reinholz & Röpke (Reference Rosmej, Reinholz and Röpke2017)). In Adams et al. (Reference Adams, Reinholz, Redmer, Mintsev, Shilkin and Gryaznov2007), on the basis of the experimentally obtained cross-sections for isolated electron–atomic scattering and data on the composition calculated by COMPTRA04, the electrical conductivity of the plasma of noble gases was estimated and good agreement with the experimental data was shown. Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017) studied the momentum-transfer cross-sections (MTCS) based on the developed optical potential over a wide range of parameters, thus avoiding already marked drawbacks of the scattering cross-sections obtained experimentally. Along with the study of electron scattering by an isolated atom, in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017) the effect of the plasma environment was also taken into account, in particular, the screening of the interaction potentials that contribute to the optical potential. Thus, they managed to obtain better agreement with experimental data on electrical conductivity in the studied ranges of temperatures and densities. It is known that screening is able to cause the significant changes in the properties of the systems under study, such as Coulomb liquids (March & Tosi Reference March and Tosi2002; Hansen & McDonald Reference Hansen and McDonald2013) or dipole systems (Aldakul, Moldabekov & Ramazanov Reference Aldakul, Moldabekov and Ramazanov2020). When screening depends on the velocities of the interacting particles, it is considered as dynamic screening. As was shown in Kremp, Ropke & Schlanges (Reference Kremp, Röpke and Schlanges1984), the dynamic screening can be taken into account in the effective interaction potentials by replacing the static Debye length with the dynamic one, which increases with the growth in the impact energy. So, when the impact energy is significantly larger than the thermal energy of the system the screening effect can be strongly weakened. In dense semiclassical plasma, in addition to collective effects, the interaction of particles is also affected by the wave properties of these particles, leading to some quantum mechanical effects (see Deutsch (Reference Deutsch1977), Deutsch, Furutani & Gombert (Reference Deutsch, Furutani and Gombert1981) and Ramazanov, Amirov & Moldabekov (Reference Ramazanov, Amirov and Moldabekov2018)). The study of the properties of dense semiclassical plasma with simultaneous consideration of the effects of screening and diffraction in the interaction of charged particles as well as in the polarization interaction of electron with an atom has been carried out in many works (see, for e.g. Jung (Reference Jung2003), Ramazanov, Dzhumagulova & Akbarov (Reference Ramazanov, Dzhumagulova and Akbarov2006a), Ramazanov, Dzhumagulova & Gabdullin (Reference Ramazanov, Dzhumagulova and Gabdullin2006b), Shalenov et al. (Reference Shalenov, Dzhumagulova, Ramazanov, Röpke and Reinholz2018b), Shalenov et al. (Reference Shalenov, Seisembayeva, Dzhumagulova and Ramazanov2019b), Shalenov et al. (Reference Shalenov, Seisembayeva, Dzhumagulova and Ramazanov2019a), Jumagulov et al. (Reference Jumagulov, Seisembayeva, Shalenov, Kossymkyzy, Ramazanov and Dzhumagulova2020) and Karmakar, Das & Ghoshal (Reference Karmakar, Das and Ghoshal2020)). It has been shown that in dense semiclassical plasma the diffraction effect arising out of the uncertainty principle can play a significant role.

It has been shown, that in dense semiclassical plasma there are the bound states within the temperature and density ranges ${10^5} \unicode{x2013} {10^6}\ {\rm K}$ and ${10^{20}}\unicode{x2013}{10^{22}}\ {\rm cm}^{-3}$ (Ramazanov et al. Reference Ramazanov, Dzhumagulova and Gabdullin2006b; Rosmej et al. Reference Rosmej, Reinholz and Röpke2017; Karmakar et al. Reference Karmakar, Das and Ghoshal2020). In this regard, it is important to reveal the influence of the diffraction effect on the collisional characteristics and then on the transport properties of such plasma. We will determine the composition of both plasma and transport properties in the next work, and in this paper we present a study of the influence of screening and diffraction effects on electron–atom scattering in dense plasma of noble gases. In order to investigate the scattering problems we constructed the optical potential of electron–atom interaction on the basis of the conclusions of Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017). This potential along with the screening effect also takes into account the diffraction effect. The calculations were carried out on the basis of the method of phase functions. The obtained results were compared with the theoretical data of other authors.

Moreover, to check the reliability of the chosen method of phase functions, we performed calculations of the scattering phase shifts on the basis of the optical potential proposed in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), where calculations had been done by the Numerov method. An agreement between results of both works is shown.

This article is organized as follows. In § 2, we describe the research method for the scattering problems. Optical potential for electron–atom interaction in dense plasma, highlighting the taking into account of screening and diffraction effects, is presented in § 3. Results, including a comparison with data of Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), are shown in § 4.

2. Phase function method

In the method of partial waves the incident particle flux is represented as a set of partial waves, which are scattered on a spherically symmetric force centre independently of each other. The contribution of each partial wave to the scattering amplitude (and hence to the differential and full scattering cross-sections) is determined by the scattering phase, the so-called phase shift ${\delta _l}$.

The scattering phase shifts can be determined from solving the radial Schrödinger equation for a particle scattered by some central field $V(r)$. In Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), the radial Schrödinger equation was solved with the Numerov method.

In this work we used another way to calculate scattering phase shifts of an incident electron. In the method of phase functions, one can pass from the Schrödinger equation to the equation directly for the scattering phases (Drukarev Reference Drukarev1965; Babikov Reference Babikov1988),

(2.1)\begin{equation} \left\{ \begin{array}{@{}l} \dfrac{{\rm d}{\delta _l}(r)}{{\rm d}r} ={-} \dfrac{1}{k}\dfrac{2m}{\hbar ^2}V(r){\left[ {\cos {\delta _l}(r) \cdot {j_l}(kr) - \sin {\delta _l}(r) \cdot {n_l}(kr)} \right]^2},\\ {\delta _l}\left( 0 \right) = 0, \end{array} \right. \end{equation}

where ${\delta _l}(r)$ is the phase function, $V(r)$ is the interaction potential, $k$ is the wavenumber of the incident electron, ${j_l}( {kr} )$ and ${n_l}( {kr} )$ are regular and irregular solutions of the Schrödinger equation. The phase shift is the asymptotical value of the phase function at large distances,

(2.2)\begin{equation} {\delta _l} = \mathop{\lim}\limits_{r \to \infty } {\delta _l}(r). \end{equation}

Note that the equation for the scattering phases has some advantages: it is much easier to solve this one than the Schrödinger equation; and the number of operations, and consequently the computation time, is also noticeably reduced.

Partial cross-sections for scattering in the quantum mechanical approximation are calculated on the basis of the phase shifts,

(2.3)\begin{equation} Q_l^P\left( k \right) = \frac{{4{\rm \pi} }}{{{k^2}}}\left( {2l + 1} \right){\sin ^2}{\delta _l}. \end{equation}

Full cross-section is defined as the sum of the partial ones, i.e.

(2.4)\begin{equation} {Q^F}\left( k \right) = \sum_{l = 0}^n {Q_l^P\left( k \right)}. \end{equation}

Momentum-transfer cross-sections, used for calculation of the transport coefficients, are also determined by the phase shifts. Thus, the transport cross-section of the first order was calculated by the following formula:

(2.5)\begin{equation} {Q^T}(k) = \frac{{4{\rm \pi} }}{{{k^2}}}\sum_{l = 0}^\infty {(l + 1){{\sin }^2}({\delta _{l + 1}} - {\delta _l})} . \end{equation}

3. Effective electron–atom interaction potential in dense semiclassical plasma

3.1. Optical potential for isolated systems

In Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), in order to determine the electron–atom MTCS the following optical potential was proposed and described in detail as the interaction potential of the isolated system:

(3.1)\begin{equation} {V_{{\rm opt}}}\left( r \right) = {V_{{\rm HF}}}\left( r \right) + {V_P}\left( r \right) + {V_{{\rm ex}}} \left(r\right). \end{equation}

The first term in this potential is called the Hartree–Fock potential $V_{{\rm HF}}(r)$, it describes the Coulomb interaction of the free electron with the nucleus as well as with electrons of the atomic shells,

(3.2)\begin{equation} {V_{{\rm HF}}}(r) = \frac{{{e^2}}}{{4{\rm \pi} {\varepsilon _0}}}\left[ { - \frac{Z}{r} + \int {\frac{1}{{\left| {{\boldsymbol{r} - }{{\boldsymbol{r}}_{\boldsymbol{1}}}} \right|}}\rho ({r_1})\,{{\rm d}^3}{{\boldsymbol{r}}_{\boldsymbol{1}}}} } \right] , \end{equation}

where $Z$ is the charge number of the nucleus and $\rho (r)$ is the density of the shell electrons.

The second term ${V_P}( r )$ describes the interaction of the free electron with the polarized atom, which prevails at large distances,

(3.3)\begin{equation} {V_P}\left( r \right) ={-} \frac{{{e^2}{\alpha _P}}}{{8{\rm \pi} {\varepsilon _0}{{\left( {r + {r_0}} \right)}^4}}}, \end{equation}

where ${\alpha _P}$ is the dipole polarizability, $r_0$ is the cutoff parameter. Its values for different atoms of noble gases are taken as the same as in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017). The introduction of the exchange term into the optical potential as a separate term is possible within the framework of a local field approximation. The replacement of the exchange kernels by an equivalent local potential makes the scattering problems much easier to solve numerically. A large number of local exchange potentials have been proposed in the literature. Systematic comparisons of some of them have been made by Yau, McEachran & Stauffer (Reference Yau, McEachran and Stauffer1978). In the free-electron–gas exchange approximation, Mittleman & Watson (Reference Mittleman and Watson1960) derived the local exchange potential,

(3.4)\begin{equation} {V_{{\rm ex}}}\left( r \right) = V_{{\rm ex}}^M\left[ {r,K\left( r \right)} \right] ={-} \frac{{{e^2}}}{{4{\rm \pi} {\varepsilon _0}}}\frac{2}{{\rm \pi} }{K_F}\left( r \right)F\left[ {\frac{{K\left( r \right)}}{{{K_F}\left( r \right)}}} \right],\end{equation}

with the Fermi momentum ${K_F}( r ) = {[ {3{{\rm \pi} ^2}\rho ( r )} ]^{{1}/{3}}}$, function $F( \eta ) = \frac {1}{2} + (({{1 - {\eta ^2}}})/{{4\eta }}) \ln | {({{\eta + 1})}/{{(\eta - 1)}}} |$, and a local-electron momentum $K(r)$, which is here taken in the version of Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017),

(3.5)\begin{equation} K_{{\rm RRR}}^2\left( r \right) = {k^2} + \frac{{2m}}{{{\hbar ^2}}}\left[ {\left| {{V_{{\rm HF}}}\left( r \right)} \right| + \left| {{V_P}\left( r \right)} \right| + \left| {V_{{\rm ex}}^M\left( {r,0} \right)} \right|} \right] , \end{equation}

where $V_{ex}^M( {r,0} ) = - ({{{e^2}}}/{{4{\rm \pi} {\varepsilon _0}}})({2}/{{\rm \pi} }){K_F}( r )$ is the momentum-free exchange term. Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017) have shown that the calculations based on (3.1) with exchange potential, (3.4), (3.5), are in better agreement with the results obtained on the basis of the static-exchange approximation (SEA), using a non-local exchange term (Duxler, Poe & Labahn Reference Duxler, Poe and Labahn1971; Pindzola & Kelly Reference Pindzola and Kelly1974), than calculations based on other approximations for $K(r)$ (Hara Reference Hara1967; Riley & Truhlar Reference Riley and Truhlar1975).

3.2. Screening and diffraction effects

It is well known that in dense non-ideal plasma the interaction of isolated particles is no longer relevant. At high densities, the average distance between particles becomes less than the Debye length,

(3.6)\begin{equation} {r_D} = \left( k_BT \left/\left( 4{\rm \pi}\,{e^2}\sum_a {{n_a}Z_a^2} \right)\right)\right.^{1/2}, \end{equation}

where $Z_a$ is the charge number of the particles of plasma component $a = e,i$. In this case, charged particles participate in collective interaction, which leads to screening of the field of individual particles. Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017) quite rightly have taken into account the screening effect of the plasma on each term of the optical potential, (3.1), and construct the screened optical potential,

(3.7)\begin{equation} V_{{\rm opt}}^s\left( r \right) = V_{{\rm HF}}^s\left( r \right) + V_P^s\left( r \right) + V_{{\rm ex}}^s\left( r \right). \end{equation}

Here, the screened polarization potential has the following form:

(3.8)\begin{equation} V_P^s\left( r \right) = {V_P}\left( r \right){{e}^{ - 2\kappa r}}{\left( {1 + \kappa r} \right)^2}, \end{equation}

where $\kappa = r_D^{ - 1}$ is the screening parameter. For the screened Hartree–Fock potential, the Coulomb interaction in (3.2) for an isolated system can be replaced by the Debye potential, and then the following expression is obtained:

(3.9)\begin{equation} V_{{\rm HF}}^s\left( r \right) = \frac{{{e^2}}}{{4{\rm \pi} {\varepsilon _0}}}\left[ { - \frac{{Z{{e}^{ - \kappa r}}}}{r} + {I_1} + {I_2} + {I_3}} \right], \end{equation}

where

(3.10)\begin{gather} {I_1} = \frac{{{{e}^{ - \kappa r}}}}{{\kappa r}}\mathop{\int}\nolimits_0^r 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{\kappa {r_1}}}\,{\rm d}{r_1}, \end{gather}
(3.11)\begin{gather}{I_2} ={-} \frac{{{{e}^{ - \kappa r}}}}{{\kappa r}}\mathop{\int}\nolimits_0^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - \kappa {r_1}}}\,{\rm d}{r_1} , \end{gather}
(3.12)\begin{gather}{I_3} = \frac{{{{e}^{\kappa r}}}}{{\kappa r}}\mathop{\int}\nolimits_r^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - \kappa {r_1}}}\,{\rm d}{r_1} . \end{gather}

To obtain the screened exchange term in (3.7), polarization and the Hartree–Fock terms in (3.5) were replaced by their screened versions, (3.8) and (3.9), respectively. On the basis of optical potential, (3.7), the influence of the screening effect on the collisional characteristics of particles in dense plasma of noble gases was investigated in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017). However, in a dense plasma, the average interparticle distance can be also comparable with the de Broglie wavelength of the particles. So, it is necessary to take into account the quantum mechanical effects, such as diffraction and symmetry, along with screening effects, for the correct description of the properties of such plasma. But, it is worth mentioning that the effect of symmetry can be neglected at high temperatures and one can only consider the diffraction and screening effects. In Ramazanov & Dzhumagulova (Reference Ramazanov and Dzhumagulova2002) the effective potential, describing interaction of the charge carriers and taking into account both effects of screening and diffraction, was presented. For the interaction of the electron and the charged particle of sort $\alpha$, it can be written as

(3.13)\begin{equation} V_{e\alpha}^{{\rm SD}}(r) ={-} \frac{{{Z_\alpha }{{e}^2}}}{{4{\rm \pi} {\varepsilon _0}C}}\left( {\frac{{{{e}^{ - B\,r}}}}{r} - \frac{{{{e}^{ - A\,r}}}}{r}} \right), \end{equation}

where ${C^2} = 1 - 4\lambda _B^2{\kappa ^2}$; ${A^2} = {1}/{{2\lambda _B^2}}( {1 + C} )$; ${B^2} = {1}/{{2\lambda _B^2}}( {1 - C} )$; and where ${\lambda _B} = \hbar /\sqrt {2{\rm \pi} {m_e}{k_B}T}$ is the thermal de Broglie wavelength of electrons. We substituted this potential into (3.2) instead of the Coulomb interaction and obtained the effective Hartree–Fock potential,

(3.14)\begin{equation} V_{{\rm HF}}^{{\rm SD}}\left( r \right) = \frac{{{{e}^2}}}{{4{\rm \pi} {\varepsilon _0}\,C}}\left[ { - \frac{{Z\left( {{{e}^{ - {Ar}}} - {{e}^{ - {Br}}}} \right)}}{{r}} + {\xi _1} + {\xi _2} + {\xi _3}} \right], \end{equation}

where

(3.15)\begin{gather} {\xi _1} =\frac{{{{e}^{ - {Ar}}}}}{{{Ar}}}\mathop{\int}\nolimits_0^r 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{{Ar}_1}}\,{\rm d}{r_1} - \frac{{{{e}^{ - {Br}}}}}{{{Br}}} \mathop{\int}\nolimits_0^r 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{{Br}_1}}\,{\rm d}{r_1}, \end{gather}
(3.16)\begin{gather}{\xi _2} ={-} \frac{{{{e}^{ - {Ar}}}}}{{{\rm Ar}}}\mathop{\int}\nolimits_0^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - A{r_1}}}\,{\rm d}{r_1} + \frac{{{{e}^{ - {Br}}}}}{{{Br}}} \mathop{\int}\nolimits_0^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - B{r_1}}}\,{\rm d}{r_1}, \end{gather}
(3.17)\begin{gather}{\xi _3} =\frac{{{{e}^{ - {Ar}}}}}{{{Ar}}}\mathop{\int}\nolimits_r^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - A{r_1}}}\,{\rm d}{r_1} - \frac{{{{e}^{ - {Br}}}}}{{{Br}}} \mathop{\int}\nolimits_r^\infty 2{\rm \pi} {r_1}\rho \left( {{r_1}} \right){{e}^{ - B{r_1}}}\,{\rm d}r. \end{gather}

The polarization potential of the interaction between an electron and an atom, taking into account the static Debye screening and the diffraction effect, was obtained in Ramazanov, Dzhumagulova & Omarbakiyeva (Reference Ramazanov, Dzhumagulova and Omarbakiyeva2005), Shalenov et al. (Reference Shalenov, Seisembayeva, Dzhumagulova, Ramazanov, Berndt, Coda, Lapenta, Michaut, Weber and Mantsinen2018a) and Dzhumagulova et al. (Reference Dzhumagulova, Shalenov, Tashkenbayev and Ramazanov2022) as

(3.18)\begin{equation} V_P^{{\rm SD}}(r) ={-} \frac{{{e^2}{\alpha _p}}}{{8{\rm \pi} {\varepsilon _0}{{(r + {r_0})}^4}{C^2}}} {\left( {{{e}^{ - {Br}}}(1 + {Br}) - {{e}^{ - {Ar}}}(1 + {Ar})} \right)^2}, \end{equation}

where $A$, $B$ and $C$ are the same quantities as in (3.13). The effective term of the exchange interaction was obtained by the already described method, when in (3.5) the Hartree–Fock and polarization contributions change to their versions, taking into account the effect of diffraction and screening, (3.14) and (3.18), respectively. Thus, after substituting all effective contributions, we have the following effective optical potential, which takes into account, along with the screening effect, the quantum mechanical effect of diffraction:

(3.19)\begin{equation} V_{{\rm opt}}^{{\rm SD}}\left( r \right) = V_{{\rm HF}}^{{\rm SD}}\left( r \right) + V_P^{{\rm SD}}\left( r \right) + V_{{\rm ex}}^{{\rm SD}}\left( r \right) . \end{equation}

It should be noted that optical potential, (3.19), transforms into potential, (3.7), at ${\lambda _B} \to 0$. Furthermore, if one neglects the effects of both screening and diffraction ($\kappa \to 0$ and ${\lambda _B} \to 0$), the optical potential (3.19) reduces to the potential of the isolated system, (3.1). Figure 1 shows the effective optical potentials, (3.19), for electron–helium (figures 1a and 1b) and electron–neon (figures 1c and 1d) interactions. The role of the screening effect in the appearance of repulsion at large distances (figures 1a and 1c) was already noted in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017). At short range, screening effects are not relevant, while the diffraction effect leads to the weakening of the attraction between electron and atom (figures 1b and 1d).

Figure 1. Effective optical potential for electron–helium (a,b) and electron–neon (c,d) interaction at zero wavenumber ($k=0$) for different screening parameters $\kappa {a_0}$ (a,c) or different de Broglie wavelengths ${\lambda _B}a_0^{ - 1}$ (b,d).

4. Results

First of all, we tested the method of phase functions using the optical potential, (3.1), for agreement with the results of Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017). For this purpose, the phase shifts for partial waves were calculated and presented in table 1. Here, the phase shifts obtained in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), in this work and the data calculated on the basis of a SEA (see Duxler et al. (Reference Duxler, Poe and Labahn1971) and Pindzola & Kelly (Reference Pindzola and Kelly1974)) were obtained using a non-local exchange term without taking into consideration the polarization potential. High agreement with the data of Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017) made it possible to conclude that the use of the chosen method of phase functions has a minimal effect on the final results.

Table 1. Electron–helium, electron–neon partial wave phase shifts ${\delta _l}$ (in rad) for calculated without taking into consideration the polarization term in the optical potential, (3.1). (1) Numerical results in SEA, Duxler et al. (Reference Duxler, Poe and Labahn1971) and Pindzola & Kelly (Reference Pindzola and Kelly1974); (2) Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017); and (3) present work.

All further presented results were obtained on the basis of the optical potential, (3.19), in order to study the simultaneous influence of the effects of screening and diffraction on the collisional characteristics in dense plasma of noble gases using the example of helium and neon. We consider the influence of the de Broglie wavelength on the results obtained; an increase in the latter is equivalent to an increase in the influence of the diffraction effect.

Figure 2 shows the phase shifts for the partial waves $l = 0$ (figures 2a and 2b) and $l = 1$ (figures 2c and 2d) arising from the collision of the electron with a helium atom. As well known, an increase in screening leads to a decrease in phase shifts. This trend can be especially seen in figure 2. The influence of the diffraction effect can be observed on all figures 2(a–d): with increasing ${\lambda _B}$ phase shifts decrease. A similar picture of the behaviour of phase shifts in the collision of the electron with a neon atom can be observed in figure 3 with the only difference that figures 3(b) and 3(d) show phase shifts, calculated at a fixed value of the de Broglie wavelength ${\lambda _B}a_0^{ - 1} = 0.25$ and different values of the screening parameter. They illustrate the fact that rising screening leads to the fall in the number of bound states following from Levinson's theorem (Wellner Reference Wellner1964; Sassoli De Bianchi Reference Sassoli De Bianchi1994; Shalenov, Dzhumagulova & Ramazanov Reference Shalenov, Dzhumagulova and Ramazanov2017).

Figure 2. Phase shifts of the electron scattering on the helium atom for $l = 0$ (a,b) and $l = 1$ (c,d) with two values of the screening parameter $\kappa {a_0}$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1}$.

Figure 3. Phase shifts of the electron scattering on the neon atom for $l = 0$ (a,b) and $l = 1$ (c,d) with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths (a,c) and with de Broglie wavelength ${\lambda _B}a_0^{ - 1} = 0.25$ at different screening parameters (b,d).

Full and partial collision cross-sections (FCS and PCS) for electron–helium and electron–neon scattering as a function of incident energy for different values of de Broglie wavelength are presented in figures 4 and 5, respectively. For electron–helium scattering, we notice that FCS is peaked when $k{a_0} \to 0$ for a given screening parameter, the height of the peak increases with rise of ${\lambda _B}$. With increasing incident energy, FCS and PCS fall. Furthermore, FCS decreases more rapidly with growing ${\lambda _B}$. In the case of electron–helium scattering, besides mentioned the above feature we can notice that in PCS for $l = 0$ the minimum's position is gradually shifted to lower energies.

Figure 4. The PCS and FCS for electron scattering on the helium atom with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1} = 0.01$ (a), ${\lambda _B}a_0^{ - 1} = 0.25$ (b), ${\lambda _B}a_0^{ - 1} = 0.50$ (c), ${\lambda _B}a_0^{ - 1} = 0.75$ (d).

Figure 5. The PCS and FCS for electron scattering on the neon atom with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1} = 0.01$ (figure 4a), ${\lambda _B}a_0^{ - 1} = 0.25$ (figure 4b), ${\lambda _B}a_0^{ - 1} = 0.50$ (figure 4c), ${\lambda _B}a_0^{ - 1} = 0.75$ (figure 4d).

In figures 6 and 7 another important scattering quantity of interest, the MTCS, is presented for helium and neon cases, respectively. It can be seen that an increase in the screening parameter, as well as in the de Broglie length, leads to an increase in MTCS at low energies. For such behaviour the diffraction effect is responsible. It is also shown that with a decrease in de Broglie wavelength, the results tend to the data obtained in Rosmej et al. (Reference Rosmej, Reinholz and Röpke2017), which do not take into account the influence of the diffraction effect.

Figure 6. The MTCS for electron scattering on the helium atom for four values of screening parameters $\kappa {a_0} = 0$ (figure 4a), $\kappa {a_0} = 0.05$ (figure 4b), $\kappa {a_0} = 0.1$ (figure 4c), $\kappa {a_0} = 0.2$ (figure 4d) at different de Broglie wavelengths.

Figure 7. The MTCS for electron scattering on the neon atom for four values of screening parameters $\kappa {a_0} = 0$ (figure 4a), $\kappa {a_0} = 0.05$ (figure 4b), $\kappa {a_0} = 0.1$ (figure 4c), $\kappa {a_0} = 0.2$ (figure 4d) at different de Broglie wavelengths.

5. Conclusion

Based on the optical potential, which takes into account the screening effect of the plasma environment in dense plasma of noble gases, we have constructed a new version that also takes into account the quantum mechanical effect of diffraction. For this purpose, as the polarization potential of the electron–atom interaction, as well as to calculate the Hartree–Fock potential, we used the potentials obtained by us earlier, and took into account both of these effects. The exchange potential was presented in the approximation of an effective local field. Within the framework of the presented model of the optical potential, the problems of electron–atom collisions were investigated using the example of helium and neon atoms. It is shown that with an increase in the de Broglie wavelength, a decrease in the phase shifts of scattering is observed at any values of the screening parameter. On the contrary, the MTCS increases with increasing de Broglie wavelength at low velocities. As the velocity increases, the screening and the quantum mechanical effect of diffraction cease to affect the MTCS. The results are shown to be in good agreement with the data of S. Rosmej in the limit when the de Broglie wavelength tends to zero.

Acknowledgements

The authors acknowledge support from the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan under grant number AP08855972. E.O.S. acknowledges support by the Postdoctoral Fellowship provided by al Farabi Kazakh National University.

Editor R. Blandford thanks the referees for their advice in evaluating this article.

Declaration of interests

The authors report no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

REFERENCES

Adams, J.R., Reinholz, H., Redmer, R., Mintsev, V.B., Shilkin, N.S. & Gryaznov, V.K. 2007 Electrical conductivity of noble gases at high pressures. Phys. Rev. E 76, 036405.CrossRefGoogle ScholarPubMed
Adibzadeh, M. & Theodosiou, C.E. 2005 Elastic electron scattering from inert-gas atoms. At. Data Nucl. Data Tables 91, 8–76.CrossRefGoogle Scholar
Aldakul, Y.K., Moldabekov, Z.A. & Ramazanov, T.S. 2020 Melting, freezing, and dynamics of two-dimensional dipole systems in screening bulk media. Phys. Rev. E 102, 033205.CrossRefGoogle ScholarPubMed
Babikov, V.V. 1988 Method of Phase Functions in Quantum Mechanics. Nauka.Google Scholar
Cho, H., McEachran, R.P., Buckman, S.J. & Tanaka, H. 2008 Elastic electron scattering from neon at backward angles. Phys. Rev. A 78, 034702.CrossRefGoogle Scholar
Deutsch, C. 1977 Nodal expansion in a real matter plasma. Phys. Lett. A 60, 317–318.CrossRefGoogle Scholar
Deutsch, C., Furutani, Y. & Gombert, M.M. 1981 Nodal expansions for strongly coupled classical plasmas. Phys. Rep. 69, 85–193.CrossRefGoogle Scholar
Drukarev, G.F. 1965 The Theory of Electron-Atom Collisions. Academic.Google Scholar
Duxler, W.M., Poe, R.T. & Labahn, R.W. 1971 Study of the polarized-orbital method and its application to the scattering of electrons by helium. Phys. Rev. A 4, 1935–1944.CrossRefGoogle Scholar
Dzhumagulova, K.N., Shalenov, E.O., Tashkenbayev, Y.A. & Ramazanov, T.S. 2022 Electron–atom interactions in dense semiclassical helium plasma. Phys. Plasmas 29, 012101.CrossRefGoogle Scholar
Hansen, J.-P. & McDonald, I.R. 2013 Theory of Simple Liquids: With Applications to Soft Matter. Academic.Google Scholar
Hara, S. 1967 The scattering of slow electrons by hydrogen molecules. J. Phys. Soc. Japan 22, 710–718.CrossRefGoogle Scholar
Jumagulov, M.N., Seisembayeva, M.M., Shalenov, E.O., Kossymkyzy, Zh., Ramazanov, T.S. & Dzhumagulova, K.N. 2020 Electron runaway in a dense semiclassical plasma. High Energy Density Phys. 36, 100832.CrossRefGoogle Scholar
Jung, Y.-D. 2003 Collective and quantum effects on elastic electron-ion collisions in strongly coupled semiclassical plasmas. Phys. Plasmas 10, 502–506.CrossRefGoogle Scholar
Karmakar, A., Das, B. & Ghoshal, A. 2020 Stability and collision dynamics of electron-proton in dense semi-classical hydrogen plasma. Phys. Plasmas 27, 103509.CrossRefGoogle Scholar
Kremp, D., Röpke, G. & Schlanges, M. 1984 Transport Properties in Dense Plasmas. Academie-Verlag.Google Scholar
Kuhlbrodt, S., Redmer, R., Reinholz, H., Röpke, G., Holst, B., Mintsev, V.B., Gryaznov, V.K., Shilkin, N.S. & Fortov, V.E. 2005 Electrical conductivity of noble gases at high pressures. Contrib. Plasma Phys. 45, 61–69.CrossRefGoogle Scholar
March, N.H. & Tosi, M.P. 2002 Introduction to Liquid State Physics. World Scientific.CrossRefGoogle Scholar
Mittleman, M.H. & Watson, K.M. 1960 Effects of the Pauli principle on the scattering of high-energy electrons by atoms. Ann. Phys. 10, 268–279.CrossRefGoogle Scholar
Pindzola, M.S. & Kelly, H.P. 1974 Low-energy scattering of electrons by the neutral argon atom. Phys. Rev. A 9, 323–331.CrossRefGoogle Scholar
Ramazanov, T.S., Amirov, S.M. & Moldabekov, Z.A. 2018 Impact of quantum non-locality and electronic non-ideality on e-He scattering in a dense plasma. Contrib. Plasma Phys. 58, 155–163.CrossRefGoogle Scholar
Ramazanov, T.S. & Dzhumagulova, K.N. 2002 Effective screened potentials of strongly coupled semiclassical plasma. Phys. Plasmas 9, 3758.CrossRefGoogle Scholar
Ramazanov, T.S., Dzhumagulova, K.N. & Akbarov, A.Zh. 2006 a Cross sections and transport coefficients of dense partially ionized semiclassical plasma. J. Phys. A: Math. Gen. 39, 4335–4340.CrossRefGoogle Scholar
Ramazanov, T.S., Dzhumagulova, K.N. & Gabdullin, M.T. 2006 b Microscopic and thermodynamic properties of dense semiclassical partially ionized hydrogen plasma. J. Phys. A: Math. Gen. 39, 4469–4474.CrossRefGoogle Scholar
Ramazanov, T.S., Dzhumagulova, K.N. & Omarbakiyeva, Y.A. 2005 Effective polarization interaction potential ‘charge-atom’ for partially ionized dense plasma. Phys. Plasmas 12, 092702.CrossRefGoogle Scholar
Ramsauer, C. 1921 über den wirkungsquerschnitt der gasmoleküle gegenüber langsamen elektronen. Ann. Phys. 369, 513–540.CrossRefGoogle Scholar
Riley, M.E. & Truhlar, D.G. 1975 Approximations for the exchange potential in electron scattering. J. Chem. Phys. 63, 2182–2191.CrossRefGoogle Scholar
Rosmej, S., Reinholz, H. & Röpke, G. 2017 Contribution of electron-atom collisions to the plasma conductivity of noble gases. Phys. Rev. E 95, 063208.CrossRefGoogle Scholar
Sassoli De Bianchi, M. 1994 Levinson's theorem, zero-energy resonances, and time delay in one-dimensional scattering systems. J. Math. Phys. (Journal of Mathematical Physics) 35, 2719–2733.Google Scholar
Shalenov, E.O., Dzhumagulova, K.N. & Ramazanov, T.S. 2017 Scattering cross sections of the particles in the partially ionized dense nonideal plasmas. Phys. Plasmas 24, 012101.CrossRefGoogle Scholar
Shalenov, E.O., Seisembayeva, M.M., Dzhumagulova, K.N. & Ramazanov, T.S. 2018 a Electron capture in the dense semiclassical plasma. In Proceedings of the International Conference ‘45th EPS Conference on Plasma Physics’ (Prague) (eds. Berndt, J., Coda, S., Lapenta, G., Michaut, C., Weber, S. & Mantsinen, M.), vol. 42A, pp. 557–560. European Physical Society (EPS).Google Scholar
Shalenov, E.O., Dzhumagulova, K.N., Ramazanov, T.S., Röpke, G. & Reinholz, H. 2018 b Dynamical conductivity of the dense semiclassical plasmas on the basis of the effective potential. Phys. Plasmas 25, 082706.CrossRefGoogle Scholar
Shalenov, E.O., Seisembayeva, M.M., Dzhumagulova, K.N. & Ramazanov, T.S. 2019 a Effect of dynamic screening on the electron capture process in nonideal plasma. J. Phys.: Conf. Ser. 1385, 012031.Google Scholar
Shalenov, E.O., Seisembayeva, M.M., Dzhumagulova, K.N. & Ramazanov, T.S. 2019 b Kinetic ionization and recombination coefficients in the dense semiclassical plasmas on the basis of the effective interaction potential. J. Phys.: Conf. Ser. 1400, 077035.Google Scholar
Townsend, J.S. & Bailey, V.A. 1922 The motion of electrons in argon. Phil. Mag. 43, 593.CrossRefGoogle Scholar
Wellner, M. 1964 Levinson's theorem (an elementary derivation). Am. J. Phys. 32, 787–789.CrossRefGoogle Scholar
Yau, A.W., McEachran, R.P. & Stauffer, A.D. 1978 Electron scattering from noble gases. J. Phys. B: At. Mol. Opt. Phys. 11, 2907–2922.CrossRefGoogle Scholar
Figure 0

Figure 1. Effective optical potential for electron–helium (a,b) and electron–neon (c,d) interaction at zero wavenumber ($k=0$) for different screening parameters $\kappa {a_0}$ (a,c) or different de Broglie wavelengths ${\lambda _B}a_0^{ - 1}$ (b,d).

Figure 1

Table 1. Electron–helium, electron–neon partial wave phase shifts ${\delta _l}$ (in rad) for calculated without taking into consideration the polarization term in the optical potential, (3.1). (1) Numerical results in SEA, Duxler et al. (1971) and Pindzola & Kelly (1974); (2) Rosmej et al. (2017); and (3) present work.

Figure 2

Figure 2. Phase shifts of the electron scattering on the helium atom for $l = 0$ (a,b) and $l = 1$ (c,d) with two values of the screening parameter $\kappa {a_0}$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1}$.

Figure 3

Figure 3. Phase shifts of the electron scattering on the neon atom for $l = 0$ (a,b) and $l = 1$ (c,d) with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths (a,c) and with de Broglie wavelength ${\lambda _B}a_0^{ - 1} = 0.25$ at different screening parameters (b,d).

Figure 4

Figure 4. The PCS and FCS for electron scattering on the helium atom with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1} = 0.01$ (a), ${\lambda _B}a_0^{ - 1} = 0.25$ (b), ${\lambda _B}a_0^{ - 1} = 0.50$ (c), ${\lambda _B}a_0^{ - 1} = 0.75$ (d).

Figure 5

Figure 5. The PCS and FCS for electron scattering on the neon atom with screening parameter $\kappa {a_0} = 0.1$ at different de Broglie wavelengths ${\lambda _B}a_0^{ - 1} = 0.01$ (figure 4a), ${\lambda _B}a_0^{ - 1} = 0.25$ (figure 4b), ${\lambda _B}a_0^{ - 1} = 0.50$ (figure 4c), ${\lambda _B}a_0^{ - 1} = 0.75$ (figure 4d).

Figure 6

Figure 6. The MTCS for electron scattering on the helium atom for four values of screening parameters $\kappa {a_0} = 0$ (figure 4a), $\kappa {a_0} = 0.05$ (figure 4b), $\kappa {a_0} = 0.1$ (figure 4c), $\kappa {a_0} = 0.2$ (figure 4d) at different de Broglie wavelengths.

Figure 7

Figure 7. The MTCS for electron scattering on the neon atom for four values of screening parameters $\kappa {a_0} = 0$ (figure 4a), $\kappa {a_0} = 0.05$ (figure 4b), $\kappa {a_0} = 0.1$ (figure 4c), $\kappa {a_0} = 0.2$ (figure 4d) at different de Broglie wavelengths.