Article contents
The stochastic tetrad magneto-hydrodynamics via functional formalism
Published online by Cambridge University Press: 02 October 2015
Abstract
In this work we discuss an application of the Tetrad Dynamics approach, a stochastic dynamical theory already introduced in hydrodynamic turbulence, to incompressible magneto-hydrodynamics. This theoretical framework is capable of taking into account some crucial aspects of turbulent plasmas, namely, (i) its material nature, which is stressed through the adoption of Lagrangian variables, (ii) its probabilistic dynamics, which is fundamental to understand the intermittency and highly irregular nature of turbulence, and (iii) the multi-scale character of interactions, which is approached by promoting the space size of parcels to the role of a dynamical variable. In particular, here, we construct the probabilistic equations of motion for quantities describing the evolution of a turbulent plasma (a matrix 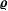 ${\bf\varrho}$ describing the parcel’s shape, the plasma velocity and magnetic field coarse-grained gradient tensors,
${\bf\varrho}$ describing the parcel’s shape, the plasma velocity and magnetic field coarse-grained gradient tensors,  $\unicode[STIX]{x1D648}$ and
$\unicode[STIX]{x1D648}$ and 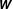 $\unicode[STIX]{x1D652}$), resorting the functional formalism of classical statistical dynamics. Through the introduction of a stochastic action and using a path integral approach, the statistical properties of
$\unicode[STIX]{x1D652}$), resorting the functional formalism of classical statistical dynamics. Through the introduction of a stochastic action and using a path integral approach, the statistical properties of 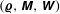 $({\bf\varrho},\unicode[STIX]{x1D648},\unicode[STIX]{x1D652})$ can be derived from those of noises appearing in their equations of motion, both at equilibrium and out of equilibrium.
$({\bf\varrho},\unicode[STIX]{x1D648},\unicode[STIX]{x1D652})$ can be derived from those of noises appearing in their equations of motion, both at equilibrium and out of equilibrium.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2015
References
- 3
- Cited by


