Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T15:11:32.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of relativistic anisotropic plasmas to perpendicular magnetosonic waves

Published online by Cambridge University Press:  13 March 2009

R. W. Landau  and
S. Cuperman
R. W. Landau
Affiliation:
Department of Physics and Astronomy and The Institute of Planetary and Space Science Tel-Aviv University, Tel-Aviv, Israel
S. Cuperman
Affiliation:
Department of Physics and Astronomy and The Institute of Planetary and Space Science Tel-Aviv University, Tel-Aviv, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of relativistic anisotropic plasmas to the magnetosonic (or righthand compressional Alfvén) wave, near the ion cyclotron frequency, propagating perpendicular to the magnetic field, is investigated. For this case, and for wavelengths larger than the ion Larmor radius and large ion plasma frequency (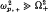) the dispersion relation is obtained in a simple form and solved. It is shown that for T‖ ╪ T⊥ (even T‖ ≥ T⊥) no instability occurs. This conclusion applies also to the case of the anisotropic interplanetary medium.

We note a peculiarity of the dispersion relation. Zero-order and first-order terms cancel so that the relation is of second order in our expansion parameter. The non-relativistic numerical results of Fredricks and Kennel are recovered.

Type
Research Article
Information
Journal of Plasma Physics , Volume 4 , Issue 3 , September 1970 , pp. 495 - 510
Copyright
Copyright © Cambridge University Press 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

Bernstein, I. B. 1958 Phys. Rev. 109, 10, Appendix I.Google Scholar
Cohen, M. H., Gundermann, E. J., Hardebeck, H. E. & Sharp, L. E. 1967 Astrophys. J. 147, 449.Google Scholar
Dessler, A. J. 1967 Rev. Geophys. 5, 1.Google Scholar
Fredricks, R. W. & Kennel, C. F. 1968 J. Geophys. Res. 73, 7429.Google Scholar
Fredricks, R. W. 1968 J. Plasma Phys. 2, 365 (especially Fig. 2).CrossRefGoogle Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 1965 Table of Integrals, Series and Products. New York: Academic Press.Google Scholar
Hamasaki, S. 1968 Phys. Fluids 11, 2724.Google Scholar
Hewish, A. & Symonds, M. D. 1969 Planet. Space Sci. 17, 313.Google Scholar
Hundhausen, A. J. 1968 Space Sci. Rev. 8, 690.CrossRefGoogle Scholar
Korablev, L. V. 1968 Soviet Phys. J.E.T.F. 5, 922.Google Scholar
Landau, R. W. & Cuperman, S. 1970 J. Plasma Phys. 4, 13.CrossRefGoogle Scholar
Macmahon, A. B. 1968 J. Geophys. Res. 73, 7538.Google Scholar
Montgomery, D. C. & Tidman, D. A. 1964 Plasma Kinetic Theory. New York: McGraw-Hill.Google Scholar
Newkirk, G. Jr 1967 Ann. Rev. Astron. Astrophys. 5, 214.Google Scholar
Parker, E. N. 1967 Plasma Astrophysics, Sturrock, P., ed., p. 239. New York: Academic Press.Google Scholar
Scarf, F. L., Fredricks, R. W. & Crook, G. M. 1968 J. Geophys. Res. 73, 1723, Fig. 8.Google Scholar
Shawhan, S. & Gurnett, D. 1968 Plasma Waves in Space and in the Lab, Thomas, J. ed., University of Edinburgh and J. Geophys. Res. 73,. 5649.Google Scholar
Stix, T. H. 1962 The Theory of Plasma Waves. New York: McGraw-Hill.Google Scholar