Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T20:22:31.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of different plasma sheaths near a dielectric wall with secondary electron emission

Published online by Cambridge University Press:  04 December 2019

Shaowei Qing Open the ORCID record for Shaowei Qing [Opens in a new window] ,
Jianguo Wei ,
Wen Chen ,
Shengli Tang  and
Xiaogang Wang
Shaowei Qing*
Affiliation:
Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Chongqing University, Ministry of Education, Chongqing400044, China Institute of Energy and Power Engineering, Chongqing University, Chongqing400044, China
Jianguo Wei
Affiliation:
Shanxi Key Laboratory of Plasma Physics and Applied Technology, Xi’an710100, China Academy of Aerospace Propulsion Technology, Xi’an710100, China
Wen Chen
Affiliation:
Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Chongqing University, Ministry of Education, Chongqing400044, China Institute of Energy and Power Engineering, Chongqing University, Chongqing400044, China
Shengli Tang
Affiliation:
Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Chongqing University, Ministry of Education, Chongqing400044, China Institute of Energy and Power Engineering, Chongqing University, Chongqing400044, China
Xiaogang Wang
Affiliation:
School of Physics, Harbin Institute of Technology, Harbin150001, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear theory stability of different collisionless plasma sheath structures, including the classic sheath, inverse sheath and space-charge limited (SCL) sheath, is investigated as a typical eigenvalue problem. The three background plasma sheaths formed between a Maxwellian plasma source and a dielectric wall with a fully self-consistent secondary electron emission condition are solved by recent developed 1D3V (one-dimensional space and three-dimensional velocities), steady-state, collisionless kinetic sheath model, within a wide range of Maxwellian plasma electron temperature 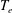$T_{e}$. Then, the eigenvalue equations of sheath plasma fluctuations through the three sheaths are numerically solved, and the corresponding damping and growth rates 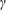$\unicode[STIX]{x1D6FE}$ are found: (i) under the classic sheath structure (i.e. 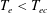$T_{e}<T_{ec}$ (the first threshold)), there are three damping solutions (i.e. 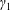$\unicode[STIX]{x1D6FE}_{1}$, 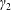$\unicode[STIX]{x1D6FE}_{2}$ and 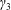$\unicode[STIX]{x1D6FE}_{3}$, 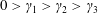$0>\unicode[STIX]{x1D6FE}_{1}>\unicode[STIX]{x1D6FE}_{2}>\unicode[STIX]{x1D6FE}_{3}$) for most cases, but there is only one growth-rate solution 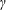$\unicode[STIX]{x1D6FE}$ when 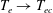$T_{e}\rightarrow T_{ec}$ due to the inhomogeneity of sheath being very weak; (ii) under the inverse sheath structure, which arises when 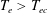$T_{e}>T_{ec}$, there are no background ions in the sheath so that the fluctuations are stable; (iii) under the SCL sheath conditions (i.e. 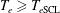$T_{e}\geqslant T_{e\text{SCL}}$, the second threshold), the obvious ion streaming through the sheath region again emerges and the three damping solutions are again found.

Keywords

plasma instabilitiesplasma sheaths
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 6 , December 2019 , 905850609
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baalrud, S. D. 2016 Influence of ion streaming instabilities on transport near plasma boundaries. Plasma Sources Sci. Technol. 25, 025008.Google Scholar
Baalrud, S. D., Callen, J. D. & Hegna, C. C. 2010 Kinetic theory of instability-enhanced collisional effects. Phys. Plasmas 17, 055704.Google Scholar
Baalrud, S. D., Hegna, C. C. & Callen, J. D. 2009 Instability-enhanced collisional friction can determine the Bohm criterion in multiple-ion-species plasmas. Phys. Rev. Lett. 103, 205002.Google Scholar
Baalrud, S. D., Lafleur, T., Fox, W. & Germaschewski, K. 2015 Instability-enhanced friction in the presheath of two-ion-species plasmas. Plasma Sources Sci. Technol. 24, 015034.Google Scholar
Barminova, H. Y. & Chikhachev, A. S. 2016 Mixed Pierce-two-stream instability development in an extraction system of a negative ion source. Rev. Sci. Instrum. 87, 02A509.Google Scholar
Bohm, D. 1949 The Characteristics of Electrical Discharges in Magnetic Fields (ed. Guthrie, A. & Wakerling, R. K.), pp. 77–86. McGraw-Hill.Google Scholar
Campanell, M. D. 2013 Negative plasma potential relative to electron-emitting surfaces. Phys. Rev. E 88, 033103.Google Scholar
Campanell, M. D. & Umansky, M. V. 2016 Strongly emitting surfaces unable to float below plasma potential. Phys. Rev. Lett. 116, 085003.Google Scholar
Campanell, M. D. & Umansky, M. V. 2017 Are two plasma equilibrium states possible when the emission coefficient exceeds unity? Phys. Plasmas 24, 057101.Google Scholar
Chen, F. F. 2016 Introduction to Plasma Physics and Controlled Fusion, 3rd edn. Springer.Google Scholar
Hershkowitz, N. 2005 Sheaths: more complicated than you think. Phys. Plasmas 12, 055502.Google Scholar
Hershkowitz, N., Ko, E., Wang, X. & Hala, A. M. A. 2005 Presheath environment in weakly ionized single and multispecies plasmas. IEEE Trans. Plasma Sci. 33, 631.Google Scholar
Hobbs, G. D. & Wesson, J. A. 1967 Heat flow through a Langmuir sheath in presence of electron emission. Plasma Phys. 9, 85.Google Scholar
Kählert, H. 2015 Ion-dust streaming instability with non-Maxwellian ions. Phys. Plasmas 22, 073703.Google Scholar
Kim, N. K., Song, J., Roh, H. J., Jang, Y., Ryu, S., Huh, S. R. & Kim, G. H. 2017 Ion-neutral collision effect on ion-ion two-stream-instability near sheath-presheath boundary in two-ion-species plasmas. Plasma Sources Sci. Technol. 26, 06LT01.Google Scholar
Kumar, A. & Mathew, V. 2017 Streaming instability in negative ion plasma. Phys. Plasmas 24, 092107.Google Scholar
Langmuir, I. 1928 Oscillations in ionized gases. Proc. Natl Acad. Sci. USA 14, 627.Google Scholar
Lee, D., Hershkowitz, N. & Severn, G. D. 2007a Measurements of Ar+ and Xe+ velocities near the sheath boundary of Ar–Xe plasma using two diode lasers. Appl. Phys. Lett. 91, 041505.Google Scholar
Lee, D., Oksuz, L. & Hershkowitz, N. 2007b Exact solution for the generalized Bohm criterion in a two-ion-species plasma. Phys. Rev. Lett. 99, 155004.Google Scholar
Lee, W. & Krasheninnikov, S. I. 2013 Secondary electron emission and the bifurcation of the heat flux to the targets in fusion plasmas. Phys. Plasmas 20, 122501.Google Scholar
Miyamoto, K. 1980 Plasma Physics for Nuclear Fusion. MIT Press.Google Scholar
Muschietti, L. & Roth, I. 2008 Ion two-stream instabilities in the auroral acceleration zone. J. Geophys. Res. 113, A08201.Google Scholar
Nitter, T., Havnes, O. & Melandsø, F. 1998 Levitation and dynamics of charged dust in the photoelectron sheath above surfaces in space. J. Geophys. Res. 103, 6605–6620.Google Scholar
Oksuz, L., Lee, D. & Hershkowitz, N. 2008 Ion acoustic wave studies near the presheath/sheath boundary in a weakly collisional argon/xenon plasma. Plasma Sources Sci. Technol. 17, 015012.Google Scholar
Qing, S. & Hu, Z. 2017 Effect of total emitted electron velocity distribution function on the plasma sheath near a floating wall. AIP Adv. 7, 085220.Google Scholar
Qing, S. & Wu, C. 2018 A detailed study on the structures of steady-state collisionless kinetic sheath near a dielectric wall with secondary electron emission. Part I. Classic sheath and its structure transition. Phys. Plasmas 25, 063519.Google Scholar
Qing, S. & Zhao, Y. 2018 A detailed study on the structures of steady-state collisionless kinetic sheath near a dielectric wall with secondary electron emission. Part II. Inverse and space-charge limited sheaths. Phys. Plasmas 25, 063520.Google Scholar
Quest, K., Rosenberg, M. & Kercher, B. 2017 Simulations of the ion-dust streaming instability with non-Maxwellian ions. J. Plasma Phys. 83, 905830612.Google Scholar
Riemann, K. U. 1991 The Bohm criterion and sheath formation. J. Phys. D: Appl. Phys. 24, 493.Google Scholar
Rosenberg, M. & Shukla, P. K. 2004 Ion-dust two-stream instability in a collisional magnetized dusty plasma. J. Plasma Phys. 70, 317–322.Google Scholar
Saleem, H. & Khan, R. 2005 Two-stream instabilities in electron-positron-ion plasmas. Phys. Scr. 71, 314–317.Google Scholar
Sheehan, J. P. & Hershkowitz, N. 2011 Emissive probes. Plasma Sources Sci. Technol. 20, 063001.Google Scholar
Sheehan, J. P., Hershkowitz, N., Kaganovich, I. D., Wang, H., Raitses, Y., Barnat, E. V., Weatherford, B. R. & Sydorenko, D. 2013 Kinetic theory of plasma sheaths surrounding electron-emitting surfaces. Phys. Rev. Lett. 111, 075002.Google Scholar
Sheehan, J. P., Kaganovich, I. D., Wang, H., Sydorenko, D., Raitses, Y. & Hershkowitz, N. 2014 Effects of emitted electron temperature on the plasma sheath. Phys. Plasmas 21, 063502.Google Scholar
Shukla, N., Shukla, P. K., Brodin, G. & Stenflo, L. 2008 Ion streaming instability in a quantum dusty magnetoplasma. Phys. Plasmas 15, 044503.Google Scholar
Sydorenko, D., Kaganovich, I., Raitses, Y. & Smolyakov, A. 2009 Breakdown of a space charge limited regime of a sheath in a weakly collisional plasma bounded by walls with secondary electron emission. Phys. Rev. Lett. 103, 145004.Google Scholar
Taccogna, F. 2014 Non-classical plasma sheaths: space-charge-limited and inverse regimes under strong emission from surfaces. Eur. Phys. J. D 68, 199.Google Scholar
Takamura, S., Ohno, N., Ye, M. Y. & Kuwabara, T. 2004 Space-charge limited current from plasma-facing material surface. Contrib. Plasma Phys. 44, 126–137.Google Scholar
Tokluoglu, E. K., Kaganovich, I. D., Carlsson, J. A., Hara, K. & Startsev, E. A. 2018 Amplification due to two-stream instability of self-electric and magnetic fields of an ion beam propagating in background plasma. Phys. Plasmas 25, 052122.Google Scholar
Tonks, L. & Langmuir, I. 1929 A general theory of the plasma of an arc. Phys. Rev. 34, 876.Google Scholar
Vaverka, J., Richterová, I., Vyšinka, M., Pavlů, J., Šafránková, J. & Němeček, Z. 2014 The influence of secondary electron emission on the floating potential of tokamak-born dust. Plasma Phys. Control. Fusion 56, 025001.Google Scholar
Wang, X. & Hershkowitz, N. 2006 Experimental studies of the two-ion species flow in the plasma presheath. Phys. Plasmas 13, 053503.Google Scholar
Zhang, Z. K. & Wang, X. G. 2012 Ion streaming instability in a plasma sheath with multiple ion species. Plasma Phys. Control. Fusion 54, 082001.Google Scholar