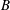PREFACE
The theory of plasma confinement is complicated and incomplete. Because current textbooks do not include material at the frontier of research, it is hard for students and researchers to become familiar with the state of the art. Bryan Taylor’s notes are presented here to start filling that gap. Although based on lectures from over twenty years ago, they provide much needed clarity in selected areas of current plasma confinement research. Of course much of the original work on which these notes are based is by Bryan Taylor and collaborators; but here, he and Sarah Newton draw the many threads together. Indeed, while some may find the results familiar, the insight is fresh and enlightening. The research frontier is just beyond these notes. Some of the outstanding questions are posed and some are left to the reader to discern. For example, we still need to know: how fast plasmas relax; how three-dimensional reconnection works; how ballooning modes saturate and; how minimum B ideas can improve toroidal devices. The insights here will help anyone wanting to answer those and other questions.
Prof S. C. Cowley FRS
CEO, United Kingdom Atomic Energy Authority
Foreword
The following notes are based on a course of lectures given by one of us (J.B.T.) at the University of Texas in Austin in 1991. As was the intention of this ‘Special Topics’ course, most of the lectures described the author’s own work. Consequently, these notes are not intended as an introductory course in plasma physics. They assume some familiarity with the subject and, as lecture notes, they are less formal than a conventional text. We hope they will be useful as a supplement to a basic course, or for advanced students, or as a record of research in the pre-computer-simulation era.
Of course, the emphasis in plasma physics has changed dramatically since 1991. Owing to time constraints, we have not attempted to bring the material up to date, though some sections, notably those on adiabatic invariants and maximal ordering theory, have been expanded.
We are grateful to Emilia Solano and Phil Edmonds, who are largely responsible for preserving the original notes, and to A. Schekochihin for encouraging their publication.
Part I
1. Introduction
In these lectures we discuss several aspects of plasma confinement in magnetic fields. Such magnetised plasmas can exhibit complex behaviour. Even if the plasma is treated as a simple conducting fluid it can exhibit all the phenomena of an ordinary fluid, including turbulence, as well as electromagnetic phenomena such as wave propagation, scattering and refraction. More importantly, a magnetised plasma exhibits many new phenomena, arising from the interaction between the plasma and the magnetic field, and it is these new phenomena that are our main interest.
1.1. Long-range effects
In reality a plasma is not a simple fluid. The idea of a simple fluid, with locally
defined properties such as diffusivity, viscosity and thermal conductivity, depends
on the fact that the mean free path of fluid particles is short. But in a
high-temperature plasma the mean free paths of ions and electrons are usually much
longer than the size of the system. Fortunately, in a magnetic field
![]() $\boldsymbol{B}$
, the paths of ions and electrons are curled into tight spirals
about the field, with (Larmor) radius
$\boldsymbol{B}$
, the paths of ions and electrons are curled into tight spirals
about the field, with (Larmor) radius
 $m_{s}v_{\bot }/e_{s}B$
– which is generally small. This tends to restore local behaviour
transverse to
$m_{s}v_{\bot }/e_{s}B$
– which is generally small. This tends to restore local behaviour
transverse to
![]() $\boldsymbol{B}$
– but the long-range effect parallel to
$\boldsymbol{B}$
– but the long-range effect parallel to
![]() $\boldsymbol{B}$
persists. This indirectly influences cross-field transport, and the
plasma may still not have unique local transport coefficients perpendicular to
$\boldsymbol{B}$
persists. This indirectly influences cross-field transport, and the
plasma may still not have unique local transport coefficients perpendicular to
![]() $\boldsymbol{B}$
. (For example, the cross-field transport in a toroidal plasma
depends on the global rotational transform.) Conversely, local changes in the
magnetic field (e.g. field line reconnection) may lead to substantial changes in the
global field structure. In a magnetised plasma ‘local changes affect global
properties and global changes affect local properties’.
$\boldsymbol{B}$
. (For example, the cross-field transport in a toroidal plasma
depends on the global rotational transform.) Conversely, local changes in the
magnetic field (e.g. field line reconnection) may lead to substantial changes in the
global field structure. In a magnetised plasma ‘local changes affect global
properties and global changes affect local properties’.
So, in any plasma confinement problem, there are two aspects to be considered. The first is the introduction of a simplified model for the plasma; the second is the incorporation of this model into a realistic configuration for the confining field.
1.2. Confinement systems
Plasma confinement systems divide sharply into two classes, according to how one
approaches the problem of loss due to flow of plasma along the magnetic field. In the
first class, one accepts free flow parallel to
![]() $\boldsymbol{B}$
, but ensures that the magnetic lines of force never leave the
system. According to an important topological theorem of Poincaré, such a system
can only be toroidal. (For a simple account of this, see Taylor
(Reference Taylor1974a
).)
$\boldsymbol{B}$
, but ensures that the magnetic lines of force never leave the
system. According to an important topological theorem of Poincaré, such a system
can only be toroidal. (For a simple account of this, see Taylor
(Reference Taylor1974a
).)
Alternatively, one may restrict the flow of plasma parallel to
![]() $\boldsymbol{B}$
by the ‘magnetic mirror’ effect (see § 16). This depends on the adiabatic invariance of the magnetic
moment
$\boldsymbol{B}$
by the ‘magnetic mirror’ effect (see § 16). This depends on the adiabatic invariance of the magnetic
moment
 ${\it\mu}=mv_{\bot }^{2}/B$
of a charged particle gyrating rapidly in a magnetic field. Because
of this, a gyrating particle of energy
${\it\mu}=mv_{\bot }^{2}/B$
of a charged particle gyrating rapidly in a magnetic field. Because
of this, a gyrating particle of energy
![]() $E$
moving along a field line into an increasing magnetic field is
reflected when
$E$
moving along a field line into an increasing magnetic field is
reflected when
 $B>2E/{\it\mu}$
. Unfortunately, this means that only particles outside the ‘loss
cone’
$B>2E/{\it\mu}$
. Unfortunately, this means that only particles outside the ‘loss
cone’
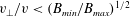 $v_{\bot }/v<(B_{min}/B_{max})^{1/2}$
in velocity space are reflected, and, as particles are continually
scattered into this loss cone, there is always significant loss of plasma through
magnetic mirrors.
$v_{\bot }/v<(B_{min}/B_{max})^{1/2}$
in velocity space are reflected, and, as particles are continually
scattered into this loss cone, there is always significant loss of plasma through
magnetic mirrors.
1.3. Plasma models
1.3.1. Fluid model
The simplest model is the ideal conducting fluid:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\frac{\text{d}\boldsymbol{v}}{\text{d}t}=\,\boldsymbol{j}\times \boldsymbol{B}-\boldsymbol{{\rm\nabla}}p, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\frac{\text{d}\boldsymbol{v}}{\text{d}t}=\,\boldsymbol{j}\times \boldsymbol{B}-\boldsymbol{{\rm\nabla}}p, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{p}\frac{\text{d}p}{\text{d}t}=\frac{{\it\gamma}}{{\it\rho}}\frac{\text{d}{\it\rho}}{\text{d}t}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{p}\frac{\text{d}p}{\text{d}t}=\frac{{\it\gamma}}{{\it\rho}}\frac{\text{d}{\it\rho}}{\text{d}t}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\rho}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\rho}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}_{0}\,\boldsymbol{j}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}_{0}\,\boldsymbol{j}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}=0. & \displaystyle\end{eqnarray}$$
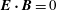 $\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
$\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
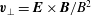 $\boldsymbol{v}_{\bot }=\boldsymbol{E}\times \boldsymbol{B}/B^{2}$
.
$\boldsymbol{v}_{\bot }=\boldsymbol{E}\times \boldsymbol{B}/B^{2}$
.
More detailed fluid models include additional effects, such as resistivity, viscosity and so-called ‘finite Larmor radius (FLR) effects’. (These are additional terms in the pressure tensor arising because particle orbits between collisions are spirals around the field lines rather than straight lines.)
Despite its simplicity and apparent deficiencies, this ideal fluid model represents large-scale plasma behaviour rather well, since the important features of anisotropy and plasma–field coupling are embodied in Ohm’s law.

Figure 1. Fluid flow in the presence of a density gradient.
1.3.2. Guiding centre model
Another simple model is based on the notion of the ‘guiding centre’. We noted that
particle orbits in a plasma are tight spirals about a magnetic field line. A
particle moves rapidly along this spiral but the spiral itself drifts slowly
across the field. Two important such ‘guiding centre drifts’ are the electric ‘
![]() $E$
cross
$E$
cross
![]() $B$
’ drift,
$B$
’ drift,
 $$\begin{eqnarray}\boldsymbol{v}_{E}=\frac{\boldsymbol{E}\times \boldsymbol{B}}{B^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{E}=\frac{\boldsymbol{E}\times \boldsymbol{B}}{B^{2}},\end{eqnarray}$$
and the magnetic ‘grad
![]() $B$
’ drift,
$B$
’ drift,
 $$\begin{eqnarray}\boldsymbol{v}_{B}=-\frac{m_{s}}{e_{s}}\frac{\boldsymbol{{\rm\nabla}}B\times \boldsymbol{B}}{B^{3}}\left(v_{\Vert }^{2}+\frac{v_{\bot }^{2}}{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{B}=-\frac{m_{s}}{e_{s}}\frac{\boldsymbol{{\rm\nabla}}B\times \boldsymbol{B}}{B^{3}}\left(v_{\Vert }^{2}+\frac{v_{\bot }^{2}}{2}\right),\end{eqnarray}$$
where subscript
![]() $s$
denotes the plasma species. Note that the electric drift is
identical for all particles, whilst the grad
$s$
denotes the plasma species. Note that the electric drift is
identical for all particles, whilst the grad
![]() $B$
drift is different, and in the opposite direction, for ions and
electrons. Note also that the guiding centre velocity and the fluid velocity are
not necessarily the same. This can be seen from figure 1. If there is a vertical density gradient, then even if the
guiding centres are at rest (
$B$
drift is different, and in the opposite direction, for ions and
electrons. Note also that the guiding centre velocity and the fluid velocity are
not necessarily the same. This can be seen from figure 1. If there is a vertical density gradient, then even if the
guiding centres are at rest (
![]() $\boldsymbol{E}=0$
), there is a non-zero fluid velocity at point A – because more
orbits are centred above A than are centred below it.
$\boldsymbol{E}=0$
), there is a non-zero fluid velocity at point A – because more
orbits are centred above A than are centred below it.
1.3.3. Kinetic theory models
The most complete description of a plasma is in terms of a phase space
distribution function
 $f_{s}(\boldsymbol{x},\boldsymbol{v},t)$
for each particle species,
$f_{s}(\boldsymbol{x},\boldsymbol{v},t)$
for each particle species,
 $$\begin{eqnarray}\frac{\partial f_{s}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f_{s}+\frac{e_{s}}{m_{s}}\left(\boldsymbol{E}+\frac{1}{c}\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }\frac{\partial f_{s}}{\partial \boldsymbol{v}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f_{s}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f_{s}+\frac{e_{s}}{m_{s}}\left(\boldsymbol{E}+\frac{1}{c}\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }\frac{\partial f_{s}}{\partial \boldsymbol{v}}=0.\end{eqnarray}$$
The system is closed by coupling the fields to Maxwell equations through the charge and current source terms,
 $$\begin{eqnarray}{\it\rho}=\mathop{\sum }_{s}e_{s}\int \text{d}^{3}v\,\,f_{s}(\boldsymbol{x},\boldsymbol{v},t),\quad \boldsymbol{j}=\mathop{\sum }_{s}e_{s}\int \text{d}^{3}v\,\boldsymbol{v}\,f_{s}(\boldsymbol{x},\boldsymbol{v},t).\end{eqnarray}$$
$$\begin{eqnarray}{\it\rho}=\mathop{\sum }_{s}e_{s}\int \text{d}^{3}v\,\,f_{s}(\boldsymbol{x},\boldsymbol{v},t),\quad \boldsymbol{j}=\mathop{\sum }_{s}e_{s}\int \text{d}^{3}v\,\boldsymbol{v}\,f_{s}(\boldsymbol{x},\boldsymbol{v},t).\end{eqnarray}$$
If the distribution function is interpreted as an assembly of discrete particles,
 $f\sim \sum _{i}{\it\delta}(\boldsymbol{x}-\boldsymbol{x}_{i}(t))\,{\it\delta}(\boldsymbol{v}-\boldsymbol{v}_{i}(t))$
, then (1.10) is
exact (but pathological and not very useful) and is known as the ‘Klimontovich
equation’. Usually,
$f\sim \sum _{i}{\it\delta}(\boldsymbol{x}-\boldsymbol{x}_{i}(t))\,{\it\delta}(\boldsymbol{v}-\boldsymbol{v}_{i}(t))$
, then (1.10) is
exact (but pathological and not very useful) and is known as the ‘Klimontovich
equation’. Usually,
 $f(\boldsymbol{x},\boldsymbol{v},t)$
is interpreted as an ensemble average, or as smoothed over a
small volume containing many particles. Then the particles are independent of one
another (except for the long-range smoothed electric and magnetic fields) and
(1.10) becomes the celebrated
‘Vlasov equation’.
$f(\boldsymbol{x},\boldsymbol{v},t)$
is interpreted as an ensemble average, or as smoothed over a
small volume containing many particles. Then the particles are independent of one
another (except for the long-range smoothed electric and magnetic fields) and
(1.10) becomes the celebrated
‘Vlasov equation’.
Mathematically, the smoothing referred to can be achieved by taking a limit in
which the discrete plasma particles are subdivided into increasingly smaller units
of mass and charge (i.e.
 $1/n\rightarrow 0$
,
$1/n\rightarrow 0$
,
![]() $e\rightarrow 0$
,
$e\rightarrow 0$
,
![]() $m\rightarrow 0$
) while maintaining
$m\rightarrow 0$
) while maintaining
![]() $e/m$
and
$e/m$
and
![]() $ne$
constant, where
$ne$
constant, where
![]() $n$
is the species’ density. This limit preserves the Debye length
$n$
is the species’ density. This limit preserves the Debye length
 ${\it\lambda}_{D}=\sqrt{{\it\epsilon}_{0}T/ne^{2}}$
and the plasma frequency
${\it\lambda}_{D}=\sqrt{{\it\epsilon}_{0}T/ne^{2}}$
and the plasma frequency
 ${\it\omega}_{p}^{2}=ne^{2}/m$
. In fact, the Vlasov equation can be regarded as the first
approximation in a hierarchy of equations (similar to the
Bogoliubov–Born–Green–Kirkwood (BBGK) hierarchy in classical fluids) ordered in
powers of a ‘discreteness’ parameter – essentially the inverse of the number of
particles in a Debye sphere
${\it\omega}_{p}^{2}=ne^{2}/m$
. In fact, the Vlasov equation can be regarded as the first
approximation in a hierarchy of equations (similar to the
Bogoliubov–Born–Green–Kirkwood (BBGK) hierarchy in classical fluids) ordered in
powers of a ‘discreteness’ parameter – essentially the inverse of the number of
particles in a Debye sphere
![]() $1/n{\it\lambda}_{D}^{3}$
(Davidson Reference Davidson1972; Nishikawa
& Wakatani Reference Nishikawa and Wakatani1993).
$1/n{\it\lambda}_{D}^{3}$
(Davidson Reference Davidson1972; Nishikawa
& Wakatani Reference Nishikawa and Wakatani1993).
Note that, although the Klimontovich and Vlasov interpretations of (1.10) share the same equation, they
are actually completely different. The Klimontovich equation involves tracking
variables
 $(\boldsymbol{x}(t),\boldsymbol{v}(t))$
and initial values
$(\boldsymbol{x}(t),\boldsymbol{v}(t))$
and initial values
 $(\boldsymbol{x}(0),\boldsymbol{v}(0))$
, whereas the Vlasov equation involves a function
$(\boldsymbol{x}(0),\boldsymbol{v}(0))$
, whereas the Vlasov equation involves a function
 $f(\boldsymbol{x},\boldsymbol{v},t)$
and initial condition
$f(\boldsymbol{x},\boldsymbol{v},t)$
and initial condition
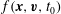 $f(\boldsymbol{x},\boldsymbol{v},t_{0})$
.
$f(\boldsymbol{x},\boldsymbol{v},t_{0})$
.
Of course, this ‘smoothing’ eliminates the short-range interactions between particles, but these can be restored by introducing ‘binary collisions’ à la Boltzmann theory of neutral gases. Then,
 $$\begin{eqnarray}\frac{\partial f_{s}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f_{s}+\frac{e_{s}}{m_{s}}\left(\boldsymbol{E}+\frac{1}{c}\,\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }\frac{\partial f_{s}}{\partial \boldsymbol{v}}=\mathop{\sum }_{s^{\prime }}C(\,f_{s},f_{s^{\prime }}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f_{s}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f_{s}+\frac{e_{s}}{m_{s}}\left(\boldsymbol{E}+\frac{1}{c}\,\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }\frac{\partial f_{s}}{\partial \boldsymbol{v}}=\mathop{\sum }_{s^{\prime }}C(\,f_{s},f_{s^{\prime }}),\end{eqnarray}$$
where
 $C(\,f_{s},f_{s^{\prime }})$
is one of several ‘collision operators’.
$C(\,f_{s},f_{s^{\prime }})$
is one of several ‘collision operators’.
Actually, collisions in a plasma are different from those in a dilute gas. In a
gas, collisions are infrequent ‘close encounters’ that scatter particles through
large angles. In a plasma, these occasional large-angle scatterings are much less
important than frequent small-angle scatterings due to ‘distant encounters’. In
fact, with a
![]() $1/r^{2}$
Coulomb interaction, the total effect of the long-range
encounters is infinite! This unfortunate feature is overcome by arguing that in a
plasma the charge of each particle is screened by a cloud of oppositely charged
particles attracted to it. This ‘Debye’ screening cloud reduces the force between
particles to
$1/r^{2}$
Coulomb interaction, the total effect of the long-range
encounters is infinite! This unfortunate feature is overcome by arguing that in a
plasma the charge of each particle is screened by a cloud of oppositely charged
particles attracted to it. This ‘Debye’ screening cloud reduces the force between
particles to
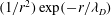 $(1/r^{2})\exp (-r/{\it\lambda}_{D})$
, where
$(1/r^{2})\exp (-r/{\it\lambda}_{D})$
, where
 ${\it\lambda}_{D}=\sqrt{{\it\epsilon}_{0}T/ne^{2}}$
is the Debye length.
${\it\lambda}_{D}=\sqrt{{\it\epsilon}_{0}T/ne^{2}}$
is the Debye length.
Although (1.12) is the most
detailed description of a plasma, it often contains more detail than is needed.
For example, one may be interested only in processes much slower than the
cyclotron frequencies
 $({\it\omega}\ll {\it\Omega})$
, or on a longer scale than the Larmor radius
$({\it\omega}\ll {\it\Omega})$
, or on a longer scale than the Larmor radius
![]() $({\it\rho}\ll {\it\lambda})$
, or of small amplitude
$({\it\rho}\ll {\it\lambda})$
, or of small amplitude
 $({\it\delta}f\ll f)$
, and the Vlasov equation can be simplified accordingly. A very
popular example of this is the ‘gyrokinetic’ model in which
$({\it\delta}f\ll f)$
, and the Vlasov equation can be simplified accordingly. A very
popular example of this is the ‘gyrokinetic’ model in which
 ${\it\omega}/{\it\Omega}\sim {\it\rho}/L\sim k_{\Vert }{\it\rho}\sim {\it\delta}f/f$
, where
${\it\omega}/{\it\Omega}\sim {\it\rho}/L\sim k_{\Vert }{\it\rho}\sim {\it\delta}f/f$
, where
![]() $L$
is the plasma scale, but
$L$
is the plasma scale, but
![]() $k_{\bot }{\it\rho}\sim 1$
so that FLR effects are retained (Catto et al.
Reference Catto, Tang and Baldwin1981).
$k_{\bot }{\it\rho}\sim 1$
so that FLR effects are retained (Catto et al.
Reference Catto, Tang and Baldwin1981).
2. Toroidal confinement
It is interesting to show that there can be no containment of a static plasma in a
purely toroidal, axisymmetric field. From the guiding centre viewpoint this is readily
demonstrated. Consider plasma centred in the minor cross-section of a toroidal vacuum
chamber (see figure 2). The grad
![]() $B$
drift is opposite for electrons and ions, so that ions accumulate on
the upper surface of the plasma at A and electrons accumulate on the lower surface at B.
These charges create an electric field and the resulting
$B$
drift is opposite for electrons and ions, so that ions accumulate on
the upper surface of the plasma at A and electrons accumulate on the lower surface at B.
These charges create an electric field and the resulting
![]() $E\times B$
drift, which is the same for both ions and electrons, then causes the
whole plasma to drift outwards away from the axis of symmetry.
$E\times B$
drift, which is the same for both ions and electrons, then causes the
whole plasma to drift outwards away from the axis of symmetry.

Figure 2. Particle motion in a toroidal field.
The corresponding proof of this from the fluid model is longer – but more informative. Starting from the equilibrium force balance
 $$\begin{eqnarray}\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p,\end{eqnarray}$$
we have
 $$\begin{eqnarray}\boldsymbol{j}=\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}+{\it\lambda}\boldsymbol{B},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}=\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}+{\it\lambda}\boldsymbol{B},\end{eqnarray}$$
where
![]() ${\it\lambda}$
is determined from
${\it\lambda}$
is determined from
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}=0$
,
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}=0$
,
 $$\begin{eqnarray}\displaystyle B\,\frac{\text{d}{\it\lambda}}{\text{d}l} & = & \displaystyle \boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right),\nonumber\\ \displaystyle & = & \displaystyle 2\,\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B}{B^{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B\,\frac{\text{d}{\it\lambda}}{\text{d}l} & = & \displaystyle \boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right),\nonumber\\ \displaystyle & = & \displaystyle 2\,\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B}{B^{3}}.\end{eqnarray}$$
Integrating around the torus on a closed field line gives the constraint
 $$\begin{eqnarray}\oint \left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B}{B^{4}}\right)\text{d}l=0.\end{eqnarray}$$
$$\begin{eqnarray}\oint \left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B}{B^{4}}\right)\text{d}l=0.\end{eqnarray}$$
However, in a purely toroidal, axisymmetric, field, the integrand is
independent of
![]() $l$
, so equilibrium requires
$l$
, so equilibrium requires
 $$\begin{eqnarray}\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0.\end{eqnarray}$$
As illustrated in figure 3, the
pressure
![]() $p$
would then have to be constant along lines parallel to the axis of
symmetry of the torus and the plasma cannot therefore be contained!
$p$
would then have to be constant along lines parallel to the axis of
symmetry of the torus and the plasma cannot therefore be contained!

Figure 3. Constant pressure surfaces in a purely toroidal field.

Figure 4. Geometry of the toroidal pinch (from Taylor Reference Taylor1986).
2.1. Magnetic surfaces
We can evade the constraint (2.4) if
we prevent the lines of force closing after one circuit of the torus. A simple way to
do this – which is the basis for the tokamak and the toroidal pinch – is to induce a
toroidal current (see figure 4). This produces a
poloidal field so that, after one circuit around the torus, a line of force is
displaced poloidally from its starting point. Then (hopefully) if the line of force
is followed indefinitely around the torus it will generate a closed ‘toroidal
magnetic surface’ (or ‘flux surface’), as shown in figure 5. The dots indicate successive intersections of a
single field line with a plane at a fixed toroidal position,
known as a Poincaré plot. The average angle,
![]() ${\it\iota}$
, between successive intersections is the ‘rotational transform’ and
the inverse of
${\it\iota}$
, between successive intersections is the ‘rotational transform’ and
the inverse of
![]() ${\it\iota}$
is the tokamak ‘safety’ factor,
${\it\iota}$
is the tokamak ‘safety’ factor,
 $q=2{\rm\pi}/{\it\iota}$
. (This is also the ratio of the number of circuits a field line
makes in the toroidal direction to the number it makes in the poloidal
direction.)
$q=2{\rm\pi}/{\it\iota}$
. (This is also the ratio of the number of circuits a field line
makes in the toroidal direction to the number it makes in the poloidal
direction.)

Figure 5. Poincaré plot generated by following a magnetic field line through many circuits around the torus.
Since
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0$
, we see that
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p=0$
, we see that
![]() $p$
must be constant over a flux surface. Therefore, what we really
require for confinement is a set of nested flux surfaces (see figure 6). Each magnetic surface is defined by
$p$
must be constant over a flux surface. Therefore, what we really
require for confinement is a set of nested flux surfaces (see figure 6). Each magnetic surface is defined by
 ${\it\Psi}(x,y,z)=\text{constant}$
, where
${\it\Psi}(x,y,z)=\text{constant}$
, where
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0$
and
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0$
and
 $p=p({\it\Psi})$
. (The degenerate surface at the centre, where we want maximum
plasma pressure, is the ‘magnetic axis’.)
$p=p({\it\Psi})$
. (The degenerate surface at the centre, where we want maximum
plasma pressure, is the ‘magnetic axis’.)

Figure 6. Nested magnetic flux surfaces.
At this point we should consider what has become of the constraint (2.4) when we have flux surfaces rather than closed field lines. There is a very useful trick for dealing with a switch from closed lines of force to a closed toroidal flux surface. Consider an integral along a line of force such as
Now introduce a thin flux tube of cross-section
![]() ${\it\delta}A$
, with flux
${\it\delta}A$
, with flux
 ${\it\delta}F=B\,{\it\delta}A$
, enclosing this field line. Then
${\it\delta}F=B\,{\it\delta}A$
, enclosing this field line. Then
 $$\begin{eqnarray}{\it\delta}F\int X\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X\,\text{d}F\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X(B\,\text{d}A)\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X\,\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}F\int X\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X\,\text{d}F\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X(B\,\text{d}A)\,\frac{\text{d}l}{B}~\Rightarrow \int _{V}X\,\text{d}{\it\tau}.\end{eqnarray}$$
Here the line integral has been converted to a volume integral. If the field line now sweeps out a surface, then the thin flux tube enclosing it sweeps out a thin shell between two adjacent toroidal flux surfaces, as shown in figure 7. So we effectively replace
 $$\begin{eqnarray}\int \frac{X}{B}\,\text{d}l~\Rightarrow \frac{\partial }{\partial {\it\Psi}}\int _{V}X\,\text{d}{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}\int \frac{X}{B}\,\text{d}l~\Rightarrow \frac{\partial }{\partial {\it\Psi}}\int _{V}X\,\text{d}{\it\tau},\end{eqnarray}$$
where
![]() $V({\it\Psi})$
is now the volume within a toroidal flux surface.
$V({\it\Psi})$
is now the volume within a toroidal flux surface.

Figure 7. Shell swept out by thin flux tube surrounding flux surface.
Applying this result to the constraint (2.4), it becomes
 $$\begin{eqnarray}\frac{\partial }{\partial {\it\Psi}}\int \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right)\text{d}{\it\tau}=\frac{\partial }{\partial {\it\Psi}}\oint \left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial }{\partial {\it\Psi}}\int \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right)\text{d}{\it\tau}=\frac{\partial }{\partial {\it\Psi}}\oint \left(\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}p}{B^{2}}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
which is automatically satisfied since
![]() $\boldsymbol{{\rm\nabla}}p$
is normal to the toroidal flux surface (i.e. parallel to
$\boldsymbol{{\rm\nabla}}p$
is normal to the toroidal flux surface (i.e. parallel to
![]() $\text{d}\boldsymbol{S}$
).
$\text{d}\boldsymbol{S}$
).
We should also see what becomes of the constraint (2.4) when the magnetic field is
non-axisymmetric. For this we write the vector potential (as we can
any vector) as
 $\boldsymbol{A}={\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta}+\boldsymbol{{\rm\nabla}}{\it\phi}$
, so
$\boldsymbol{A}={\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta}+\boldsymbol{{\rm\nabla}}{\it\phi}$
, so
 $\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta}$
. The functions
$\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta}$
. The functions
 ${\it\alpha}(x,y,z)$
and
${\it\alpha}(x,y,z)$
and
 ${\it\beta}(x,y,z)$
, known as Clebsch variables, are constant along a field line and
the pressure is a function
${\it\beta}(x,y,z)$
, known as Clebsch variables, are constant along a field line and
the pressure is a function
 $p=p({\it\alpha},{\it\beta})$
. Then we have
$p=p({\it\alpha},{\it\beta})$
. Then we have
 $$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p\times \boldsymbol{{\rm\nabla}}B=\left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial B}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial B}{\partial {\it\alpha}}\right)B^{2}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p\times \boldsymbol{{\rm\nabla}}B=\left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial B}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial B}{\partial {\it\alpha}}\right)B^{2}\end{eqnarray}$$
and (2.4) becomes
 $$\begin{eqnarray}\oint \left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial B}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial B}{\partial {\it\alpha}}\right)\frac{\text{d}l}{B^{2}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\oint \left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial B}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial B}{\partial {\it\alpha}}\right)\frac{\text{d}l}{B^{2}}=0.\end{eqnarray}$$
Remembering that
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
are constant along
${\it\beta}$
are constant along
![]() $\text{d}l$
, this implies
$\text{d}l$
, this implies
 $$\begin{eqnarray}\left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial U}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial U}{\partial {\it\alpha}}\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{\partial p}{\partial {\it\alpha}}\frac{\partial U}{\partial {\it\beta}}-\frac{\partial p}{\partial {\it\beta}}\frac{\partial U}{\partial {\it\alpha}}\right)=0,\end{eqnarray}$$
where
 $$\begin{eqnarray}U\equiv \oint \frac{\text{d}l}{B}.\end{eqnarray}$$
$$\begin{eqnarray}U\equiv \oint \frac{\text{d}l}{B}.\end{eqnarray}$$
Hence, in a toroidal system with closed, but not necessarily purely
toroidal, field lines, equation (2.4) imposes the constraint
 $p\equiv p(U)$
.
$p\equiv p(U)$
.
In conclusion, therefore, the consequences of the equilibrium force balance
 $\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
in a torus are:
$\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
in a torus are:
-
(i) If field lines generate flux surfaces
 ${\it\Psi}$
, then
${\it\Psi}$
, then
 $p=p({\it\Psi})$
.
$p=p({\it\Psi})$
. -
(ii) If field lines close,
 $p$
is constant along
$p$
is constant along
 $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
 $p=p(U)$
, where
$p=p(U)$
, where
 $U=\oint \text{d}l/B$
.
$U=\oint \text{d}l/B$
.
This means that, in a non-axisymmetric torus, there is a potential conflict between
the constraints
 $p=p({\it\Psi})$
and
$p=p({\it\Psi})$
and
 $p=p(U)$
at the so-called ‘rational surfaces’ where the rotational transform
$p=p(U)$
at the so-called ‘rational surfaces’ where the rotational transform
 ${\it\iota}=2{\rm\pi}m/n$
with
${\it\iota}=2{\rm\pi}m/n$
with
![]() $m$
and
$m$
and
![]() $n$
integers and the lines of force close after
$n$
integers and the lines of force close after
![]() $n$
circuits. Mathematically, these rational surfaces have zero measure
compared to the irrational surfaces. Obviously, the simple fluid model is inadequate
to discuss such fine details. Nevertheless, low-order rational surfaces (where
$n$
circuits. Mathematically, these rational surfaces have zero measure
compared to the irrational surfaces. Obviously, the simple fluid model is inadequate
to discuss such fine details. Nevertheless, low-order rational surfaces (where
![]() $m$
and
$m$
and
![]() $n$
are small) play an important role in the stability of toroidal
plasmas.
$n$
are small) play an important role in the stability of toroidal
plasmas.
2.2. Magnetic surfaces and the Grad–Shafranov equation
We saw that for good containment we need an equilibrium with closed toroidal magnetic
surfaces. But do solutions of
 $\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
with closed magnetic surfaces really exist? In general this is a
difficult question, related to the Kolmogorov–Arnold–Moser (KAM) theorem and
mathematical chaos, and further complicated by the conflict mentioned above. However,
solutions do exist in an axisymmetric torus and in other
configurations with an ignorable coordinate (Grad & Rubin Reference Grad and Rubin1958).
$\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
with closed magnetic surfaces really exist? In general this is a
difficult question, related to the Kolmogorov–Arnold–Moser (KAM) theorem and
mathematical chaos, and further complicated by the conflict mentioned above. However,
solutions do exist in an axisymmetric torus and in other
configurations with an ignorable coordinate (Grad & Rubin Reference Grad and Rubin1958).
2.2.1. Cylindrical
The simplest magnetic surfaces are those in a straight cylinder where, in
cylindrical coordinates
![]() $(r,{\it\theta},z)$
, the field is independent of
$(r,{\it\theta},z)$
, the field is independent of
![]() $z$
and we can therefore write it as
$z$
and we can therefore write it as
 $$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,{\it\theta})+\boldsymbol{n}_{z}\,f(r,{\it\theta}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,{\it\theta})+\boldsymbol{n}_{z}\,f(r,{\it\theta}),\end{eqnarray}$$
where
![]() $\boldsymbol{n}_{z}$
is a unit vector in the
$\boldsymbol{n}_{z}$
is a unit vector in the
![]() $z$
direction. Then
$z$
direction. Then
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
and
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0$
, so if
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0$
, so if
![]() ${\it\Psi}$
exists it is a magnetic surface. To
find the surface
${\it\Psi}$
exists it is a magnetic surface. To
find the surface
![]() ${\it\Psi}$
, we start from the equilibrium
${\it\Psi}$
, we start from the equilibrium
 $\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
. Then we know that
$\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}p$
. Then we know that
![]() $p$
must be a function of
$p$
must be a function of
![]() ${\it\Psi}$
. Using the expression (2.14) for the field, the current is
${\it\Psi}$
. Using the expression (2.14) for the field, the current is
 $$\begin{eqnarray}\boldsymbol{j}=\boldsymbol{n}_{z}{\rm\nabla}^{2}{\it\Psi}-\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}=\boldsymbol{n}_{z}{\rm\nabla}^{2}{\it\Psi}-\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f,\end{eqnarray}$$
so that for equilibrium
![]() ${\it\Psi}$
must satisfy
${\it\Psi}$
must satisfy
 $$\begin{eqnarray}({\rm\nabla}^{2}{\it\Psi})\boldsymbol{{\rm\nabla}}{\it\Psi}+(\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi})\boldsymbol{n}_{z}+f\boldsymbol{{\rm\nabla}}f+p^{\prime }\boldsymbol{{\rm\nabla}}{\it\Psi}=0.\end{eqnarray}$$
$$\begin{eqnarray}({\rm\nabla}^{2}{\it\Psi})\boldsymbol{{\rm\nabla}}{\it\Psi}+(\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi})\boldsymbol{n}_{z}+f\boldsymbol{{\rm\nabla}}f+p^{\prime }\boldsymbol{{\rm\nabla}}{\it\Psi}=0.\end{eqnarray}$$
The component of (2.16) parallel to
![]() $\boldsymbol{n}_{z}$
requires
$\boldsymbol{n}_{z}$
requires
 $$\begin{eqnarray}\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{n}_{z}\times \boldsymbol{{\rm\nabla}}f\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Psi}=0,\end{eqnarray}$$
so that
![]() $f$
must also be a function only of
$f$
must also be a function only of
![]() ${\it\Psi}$
. The component of (2.16) perpendicular to
${\it\Psi}$
. The component of (2.16) perpendicular to
![]() $\boldsymbol{n}_{z}$
then gives an equation for
$\boldsymbol{n}_{z}$
then gives an equation for
![]() ${\it\Psi}$
,
${\it\Psi}$
,
 $$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial {\it\Psi}}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}{\it\Psi}}{\partial {\it\theta}^{2}}+p^{\prime }({\it\Psi})+f\,f^{\prime }({\it\Psi})=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial {\it\Psi}}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}{\it\Psi}}{\partial {\it\theta}^{2}}+p^{\prime }({\it\Psi})+f\,f^{\prime }({\it\Psi})=0.\end{eqnarray}$$
This is known as the Grad–Shafranov equationFootnote
2
for equilibrium in a cylinder – a two-dimensional partial differential
equation. Solutions can be found once reasonable pressure and flux functions,
![]() $p({\it\Psi})$
and
$p({\it\Psi})$
and
![]() $f({\it\Psi})$
, and boundary conditions, are specified.
$f({\it\Psi})$
, and boundary conditions, are specified.
2.2.2. Toroidal
Of course, an infinite cylinder is not very practicable, but it illustrates how to
proceed in more realistic cases. A very important case is the axisymmetric torus –
an idealisation of a tokamak or toroidal pinch. In this case the field is
independent of
![]() ${\it\phi}$
in
${\it\phi}$
in
![]() $(r,{\it\phi},z)$
coordinates and we can write it as
$(r,{\it\phi},z)$
coordinates and we can write it as
 $$\begin{eqnarray}\boldsymbol{B}=\frac{1}{r}[\boldsymbol{n}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}{\it\psi}(r,z)+\boldsymbol{n}_{{\it\phi}}F(r,z)]\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\frac{1}{r}[\boldsymbol{n}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}{\it\psi}(r,z)+\boldsymbol{n}_{{\it\phi}}F(r,z)]\end{eqnarray}$$
and the current is
 $$\begin{eqnarray}\boldsymbol{j}=-\frac{1}{r}[\boldsymbol{n}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}(rB_{{\it\phi}})\times +\boldsymbol{n}_{{\it\phi}}{\rm\Delta}^{\ast }{\it\Psi}],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}=-\frac{1}{r}[\boldsymbol{n}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}(rB_{{\it\phi}})\times +\boldsymbol{n}_{{\it\phi}}{\rm\Delta}^{\ast }{\it\Psi}],\end{eqnarray}$$
where
 ${\rm\Delta}^{\ast }=r^{2}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(r^{-2}\boldsymbol{{\rm\nabla}}{\it\Psi})$
. As in the cylindrical case, equilibrium then requires
${\rm\Delta}^{\ast }=r^{2}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(r^{-2}\boldsymbol{{\rm\nabla}}{\it\Psi})$
. As in the cylindrical case, equilibrium then requires
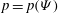 $p=p({\it\Psi})$
and
$p=p({\it\Psi})$
and
 $F=F({\it\Psi})$
and the equation for equilibrium in an axisymmetric torus
becomes
$F=F({\it\Psi})$
and the equation for equilibrium in an axisymmetric torus
becomes
 $$\begin{eqnarray}r\frac{\partial }{\partial r}\frac{1}{r}\frac{\partial {\it\Psi}}{\partial r}+\frac{\partial ^{2}{\it\Psi}}{\partial z^{2}}+r^{2}p^{\prime }({\it\Psi})+FF^{\prime }({\it\Psi})=0.\end{eqnarray}$$
$$\begin{eqnarray}r\frac{\partial }{\partial r}\frac{1}{r}\frac{\partial {\it\Psi}}{\partial r}+\frac{\partial ^{2}{\it\Psi}}{\partial z^{2}}+r^{2}p^{\prime }({\it\Psi})+FF^{\prime }({\it\Psi})=0.\end{eqnarray}$$
This is again a two-dimensional partial differential equation with
solutions specified by two arbitrary functions
![]() $p({\it\Psi})$
and
$p({\it\Psi})$
and
![]() $F({\it\Psi})$
and appropriate boundary conditions. A simple example is given
below.
$F({\it\Psi})$
and appropriate boundary conditions. A simple example is given
below.
2.2.3. An example
A simple example of toroidal equilibrium is given by (2.21), with
 $$\begin{eqnarray}\displaystyle & p=8(1+{\it\alpha}^{2}){\it\Psi}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & p=8(1+{\it\alpha}^{2}){\it\Psi}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & F=\text{constant}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & F=\text{constant}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}r\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial {\it\Psi}}{\partial r}\right)+\frac{\partial ^{2}{\it\Psi}}{\partial z^{2}}+8r^{2}(1+{\it\alpha}^{2})=0,\end{eqnarray}$$
$$\begin{eqnarray}r\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial {\it\Psi}}{\partial r}\right)+\frac{\partial ^{2}{\it\Psi}}{\partial z^{2}}+8r^{2}(1+{\it\alpha}^{2})=0,\end{eqnarray}$$
with a solution
 $$\begin{eqnarray}{\it\Psi}=r^{2}(2R^{2}-r^{2}-4{\it\alpha}^{2}z^{2}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\Psi}=r^{2}(2R^{2}-r^{2}-4{\it\alpha}^{2}z^{2}).\end{eqnarray}$$
In this case, the magnetic surfaces are toroids of approximately
elliptical cross-section (see figure 8),
surrounding the magnetic axis at
![]() $r=R$
and bearing some resemblance to the shape of modern
tokamaks.
$r=R$
and bearing some resemblance to the shape of modern
tokamaks.
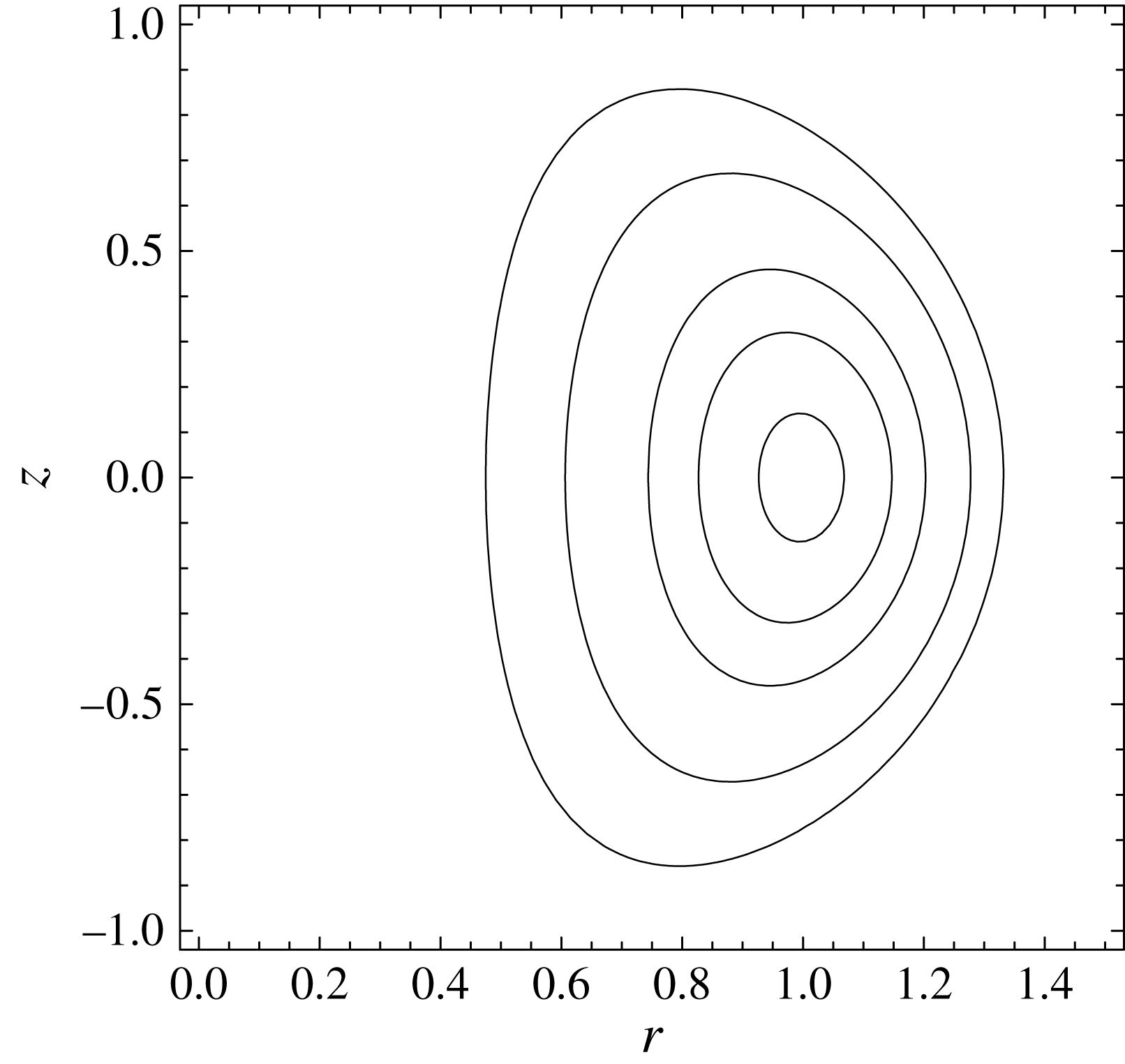
Figure 8. Cross-section of magnetic surfaces defined by (2.25), for
 $R=1~\text{m}$
and
$R=1~\text{m}$
and
![]() ${\it\alpha}=0.5$
.
${\it\alpha}=0.5$
.

Figure 9. Sketch of a stellarator configuration.
2.2.4. Helical
There is a similar equation to (2.21) for an equilibrium with helical symmetry (Freidberg Reference Freidberg2014). This represents a ‘straight’ version of
a stellarator (see figure 9), where the field
in
![]() $(r,{\it\theta},z)$
coordinates depends only on
$(r,{\it\theta},z)$
coordinates depends only on
![]() $r$
and
$r$
and
 $u=(l{\it\theta}+kz)$
. This helical problem can be treated in a similar way to the
cylindrical and toroidal problems by introducing a vector
$u=(l{\it\theta}+kz)$
. This helical problem can be treated in a similar way to the
cylindrical and toroidal problems by introducing a vector
 $$\begin{eqnarray}\boldsymbol{h}=\frac{(l\boldsymbol{n}_{z}-kr\boldsymbol{n}_{{\it\theta}})}{(l^{2}+k^{2}r^{2})^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{h}=\frac{(l\boldsymbol{n}_{z}-kr\boldsymbol{n}_{{\it\theta}})}{(l^{2}+k^{2}r^{2})^{1/2}}.\end{eqnarray}$$
(Note that
![]() $\boldsymbol{n}_{z}$
,
$\boldsymbol{n}_{z}$
,
![]() $\boldsymbol{n}_{{\it\theta}}$
and
$\boldsymbol{n}_{{\it\theta}}$
and
![]() $\boldsymbol{h}$
are all unit vectors.) Then the field can be written as
$\boldsymbol{h}$
are all unit vectors.) Then the field can be written as
 $$\begin{eqnarray}\boldsymbol{B}=\frac{1}{(l^{2}+k^{2}r^{2})^{1/2}}[\boldsymbol{h}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,u)+\boldsymbol{h}F(r,u)]\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\frac{1}{(l^{2}+k^{2}r^{2})^{1/2}}[\boldsymbol{h}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,u)+\boldsymbol{h}F(r,u)]\end{eqnarray}$$
and, after some algebra,
![]() $F$
and
$F$
and
![]() $p$
are again found to be functions only of
$p$
are again found to be functions only of
![]() ${\it\Psi}$
, and the equation for helical equilibrium is
${\it\Psi}$
, and the equation for helical equilibrium is
 $$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\frac{r}{(l^{2}+k^{2}r^{2})}\frac{\partial {\it\Psi}}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}{\it\Psi}}{\partial u^{2}}+p^{\prime }({\it\Psi})+\frac{FF^{\prime }({\it\Psi})}{(l^{2}+k^{2}r^{2})}-\frac{2klF({\it\Psi})}{(l^{2}+k^{2}r^{2})^{2}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\frac{r}{(l^{2}+k^{2}r^{2})}\frac{\partial {\it\Psi}}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}{\it\Psi}}{\partial u^{2}}+p^{\prime }({\it\Psi})+\frac{FF^{\prime }({\it\Psi})}{(l^{2}+k^{2}r^{2})}-\frac{2klF({\it\Psi})}{(l^{2}+k^{2}r^{2})^{2}}=0.\end{eqnarray}$$
(It is important in this case not to confuse the fixed pitch
![]() $k$
of the helical symmetry, imposed by boundary conditions, with
the pitch of the lines of force – which varies from flux surface to flux surface;
see § 3.)
$k$
of the helical symmetry, imposed by boundary conditions, with
the pitch of the lines of force – which varies from flux surface to flux surface;
see § 3.)
The three cases described above comprise the only exact magnetohydrodynamic (MHD) equilibria and only the toroidal case represents a realistic situation (the others extend to infinity).
2.3. Rotational transform
An important property of a toroidal magnetic surface is its rotational transform
![]() ${\it\iota}({\it\Psi})$
, or safety factor
${\it\iota}({\it\Psi})$
, or safety factor
 $q=2{\rm\pi}/{\it\iota}$
. Indeed, a rotational transform is essential for toroidal
confinement (see § 2.1). In general,
$q=2{\rm\pi}/{\it\iota}$
. Indeed, a rotational transform is essential for toroidal
confinement (see § 2.1). In general,
 $$\begin{eqnarray}\frac{{\it\iota}({\it\Psi})}{2{\rm\pi}}\equiv \lim \left(\frac{\text{number of circuits made by line of force in poloidal direction}}{\text{number of circuits made in toroidal direction}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\iota}({\it\Psi})}{2{\rm\pi}}\equiv \lim \left(\frac{\text{number of circuits made by line of force in poloidal direction}}{\text{number of circuits made in toroidal direction}}\right),\end{eqnarray}$$
where the limit is as the number of circuits
![]() $\rightarrow \infty$
. The simplest configuration in which a rotational transform appears
is a circular cylinder, with periodicity
$\rightarrow \infty$
. The simplest configuration in which a rotational transform appears
is a circular cylinder, with periodicity
![]() $2{\rm\pi}R$
, to simulate a torus. In this case each field line is a uniform
spiral about the
$2{\rm\pi}R$
, to simulate a torus. In this case each field line is a uniform
spiral about the
![]() $z$
axis,
$z$
axis,
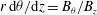 $r\,\text{d}{\it\theta}/\text{d}z=B_{{\it\theta}}/B_{z}$
. The magnetic surfaces are circular cylinders and
$r\,\text{d}{\it\theta}/\text{d}z=B_{{\it\theta}}/B_{z}$
. The magnetic surfaces are circular cylinders and
 $$\begin{eqnarray}\frac{{\it\iota}({\it\Psi})}{2{\rm\pi}}=\frac{B_{{\it\theta}}R}{rB_{z}}=\frac{I_{z}}{{\it\psi}_{z}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\iota}({\it\Psi})}{2{\rm\pi}}=\frac{B_{{\it\theta}}R}{rB_{z}}=\frac{I_{z}}{{\it\psi}_{z}},\end{eqnarray}$$
where
![]() $I_{z}$
and
$I_{z}$
and
![]() ${\it\psi}_{z}$
are the current and flux within the surface. Note that this does
not depend on the presence of plasma – the current
${\it\psi}_{z}$
are the current and flux within the surface. Note that this does
not depend on the presence of plasma – the current
![]() $I_{z}$
may as well flow in a thin wire along the
$I_{z}$
may as well flow in a thin wire along the
![]() $z$
axis.
$z$
axis.
Of course, this is trivial; everyone knows an axial current generates an encircling field! What is not trivial is that if we add an externally generated helical field (to resemble a straight stellarator) then a rotational transform exists without any axial current!
One can be forgiven if initially this appears to contradict Ampere’s law, for if we
take a circular loop integral around the
![]() $z$
axis,
$z$
axis,
 $\oint rB_{{\it\theta}}\,\text{d}{\it\theta}$
must vanish when there is no axial current. This paradox is
resolved if we note that the helical field modulates
$\oint rB_{{\it\theta}}\,\text{d}{\it\theta}$
must vanish when there is no axial current. This paradox is
resolved if we note that the helical field modulates
![]() $B_{{\it\theta}}$
, so that a loop round a flux surface has fluctuating
$B_{{\it\theta}}$
, so that a loop round a flux surface has fluctuating
![]() $r$
and
$r$
and
![]() $B_{{\it\theta}}$
. To first order these fluctuations cancel, but a second-order
effect remains.
$B_{{\it\theta}}$
. To first order these fluctuations cancel, but a second-order
effect remains.
A detailed calculation (Johnson et al.
Reference Johnson1958; Spitzer Reference Spitzer1958) shows that a helical field
 ${\sim}B_{hel}\cos (l{\it\theta}+kz)$
generates a rotational transform
${\sim}B_{hel}\cos (l{\it\theta}+kz)$
generates a rotational transform
 ${\it\iota}\sim r^{2l-4}(B_{hel}^{2}/B_{tor}^{2})[2(l-1)+k^{2}r^{2}]$
near the magnetic axis. The transform therefore differs according
to whether
${\it\iota}\sim r^{2l-4}(B_{hel}^{2}/B_{tor}^{2})[2(l-1)+k^{2}r^{2}]$
near the magnetic axis. The transform therefore differs according
to whether
![]() $l=1$
(when it vanishes on the axis and increases slowly with minor
radius
$l=1$
(when it vanishes on the axis and increases slowly with minor
radius
![]() $r$
),
$r$
),
![]() $l=2$
(when the transform is finite near the axis and increases slowly
with
$l=2$
(when the transform is finite near the axis and increases slowly
with
![]() $r$
) or
$r$
) or
![]() $l\geqslant 3$
(when the transform vanishes on the axis and increases rapidly with
$l\geqslant 3$
(when the transform vanishes on the axis and increases rapidly with
![]() $r$
). These differences are important for plasma stability and
$r$
). These differences are important for plasma stability and
![]() $l=3$
is usually a preferred value – because shear in the rotational
transform generally enhances stability.
$l=3$
is usually a preferred value – because shear in the rotational
transform generally enhances stability.
Surprisingly, neither axial current nor helical windings are
necessary for a rotational transform! Indeed, the original
suggestion for generating a rotational transform (Spitzer Reference Spitzer1951) was to take a simple toroidal solenoid, with no additional
currents or fields, and to ‘twist’ it into a figure-of-eight (see figure 10). In fact, any solenoidal field with a twisted
magnetic axis generates a rotational transform. This is purely a geometrical effect
and
![]() ${\it\iota}$
is the integral of the torsion around the (closed) magnetic axis,
independent of minor radius.
${\it\iota}$
is the integral of the torsion around the (closed) magnetic axis,
independent of minor radius.

Figure 10. Sketch of figure-eight stellarator. (Reproduced with permission from Spitzer (Reference Spitzer1958). Copyright 1958, AIP Publishing LLC.)
3. Perturbations of symmetry
We have seen that, at least in principle, flux surfaces exist in systems with an
ignorable coordinate. Now let us look in more detail at the effect of perturbations of
this symmetry. Consider the field in a section of an infinite circular cylinder (of
length
![]() $2{\rm\pi}R$
to represent toroidal periodicity). In coordinates
$2{\rm\pi}R$
to represent toroidal periodicity). In coordinates
![]() $(r,{\it\theta},z)$
this has symmetry in both
$(r,{\it\theta},z)$
this has symmetry in both
![]() ${\it\theta}$
and
${\it\theta}$
and
![]() $z$
. The magnetic field has components
$z$
. The magnetic field has components
![]() $B_{r}=0$
,
$B_{r}=0$
,
 $B_{{\it\theta}}=B_{{\it\theta}}(r)$
and
$B_{{\it\theta}}=B_{{\it\theta}}(r)$
and
 $B_{z}=B_{z}(r)$
, creating cylindrical flux surfaces
$B_{z}=B_{z}(r)$
, creating cylindrical flux surfaces
![]() ${\it\Psi}(r)$
with rotational transform (over the
${\it\Psi}(r)$
with rotational transform (over the
![]() $2{\rm\pi}R$
section)
$2{\rm\pi}R$
section)
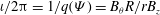 ${\it\iota}/2{\rm\pi}=1/q({\it\Psi})=B_{{\it\theta}}R/rB_{z}$
.
${\it\iota}/2{\rm\pi}=1/q({\it\Psi})=B_{{\it\theta}}R/rB_{z}$
.
Any perturbation of this cylindrical field can be decomposed into helical components
 ${\sim}\exp [\text{i}(m{\it\theta}+kz)]$
, where
${\sim}\exp [\text{i}(m{\it\theta}+kz)]$
, where
 $k=-n/2{\rm\pi}R$
. We first examine the effect of a single such helical component. Then
the combined field has helical symmetry. As we mentioned earlier, the pitch of this
helical symmetry is in general different from the pitch of the unperturbed field lines,
but on a ‘resonant surface’, where
$k=-n/2{\rm\pi}R$
. We first examine the effect of a single such helical component. Then
the combined field has helical symmetry. As we mentioned earlier, the pitch of this
helical symmetry is in general different from the pitch of the unperturbed field lines,
but on a ‘resonant surface’, where
 $m-nq({\it\Psi})=0$
, the helical perturbation and the unperturbed field lines have the
same pitch.
$m-nq({\it\Psi})=0$
, the helical perturbation and the unperturbed field lines have the
same pitch.
As in § 2.2.4, the combined field can be written as
 $$\begin{eqnarray}\boldsymbol{B}=\frac{1}{(m^{2}+k^{2}r^{2})^{1/2}}[\boldsymbol{h}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,u)+\boldsymbol{h}F(r,u)],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\frac{1}{(m^{2}+k^{2}r^{2})^{1/2}}[\boldsymbol{h}\times \boldsymbol{{\rm\nabla}}{\it\Psi}(r,u)+\boldsymbol{h}F(r,u)],\end{eqnarray}$$
where
 $u=(m{\it\theta}+kz)$
and
$u=(m{\it\theta}+kz)$
and
![]() $\boldsymbol{h}$
is the unit vector
$\boldsymbol{h}$
is the unit vector
 $$\begin{eqnarray}\boldsymbol{h}=\frac{(l\boldsymbol{n}_{z}-kr\boldsymbol{n}_{{\it\theta}})}{(l^{2}+k^{2}r^{2})^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{h}=\frac{(l\boldsymbol{n}_{z}-kr\boldsymbol{n}_{{\it\theta}})}{(l^{2}+k^{2}r^{2})^{1/2}}.\end{eqnarray}$$
The flux surfaces
![]() ${\it\Psi}$
of the combined field will have the form
${\it\Psi}$
of the combined field will have the form
 $$\begin{eqnarray}{\it\Psi}={\it\Psi}_{0}(r)+{\it\psi}(r)\cos (m{\it\theta}+kz)\end{eqnarray}$$
$$\begin{eqnarray}{\it\Psi}={\it\Psi}_{0}(r)+{\it\psi}(r)\cos (m{\it\theta}+kz)\end{eqnarray}$$
and we can expect the effect of the helical perturbation to be important
near a resonant surface, when the perturbation is constant along the unperturbed field
(otherwise the effect of the perturbation is largely averaged out). From (3.1) the radius
![]() $r_{0}$
of the resonant surface is determined by
$r_{0}$
of the resonant surface is determined by
 $\partial {\it\Psi}_{0}/\partial r=0$
and near this surface we can write (3.3) as
$\partial {\it\Psi}_{0}/\partial r=0$
and near this surface we can write (3.3) as
 $$\begin{eqnarray}{\it\Psi}={\textstyle \frac{1}{2}}{\it\Psi}_{0}^{\prime \prime }(r-r_{0})^{2}+{\it\psi}\cos (m{\it\theta}+kz).\end{eqnarray}$$
$$\begin{eqnarray}{\it\Psi}={\textstyle \frac{1}{2}}{\it\Psi}_{0}^{\prime \prime }(r-r_{0})^{2}+{\it\psi}\cos (m{\it\theta}+kz).\end{eqnarray}$$
The cross-sections of the corresponding surfaces, at fixed
![]() $z$
, are shown in figure 11 for
perturbations with
$z$
, are shown in figure 11 for
perturbations with
![]() $m=3$
and
$m=3$
and
![]() $m=7$
symmetry. As expected, most of the original surfaces are only slightly
deformed by the perturbation, but the resonant surface is broken up to form a chain of
‘islands’. The width of an island can be estimated from (3.4) as
$m=7$
symmetry. As expected, most of the original surfaces are only slightly
deformed by the perturbation, but the resonant surface is broken up to form a chain of
‘islands’. The width of an island can be estimated from (3.4) as
 $$\begin{eqnarray}{\it\Delta}=4\left[\frac{{\it\psi}}{{\it\Psi}_{0}^{\prime \prime }(r_{0})}\right]^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\Delta}=4\left[\frac{{\it\psi}}{{\it\Psi}_{0}^{\prime \prime }(r_{0})}\right]^{1/2}.\end{eqnarray}$$
A more practical form of this result is obtained using (3.1), which shows
 ${\it\delta}B_{r}\sim \partial {\it\Psi}/\partial {\it\theta}\sim m{\it\psi}/r$
and
${\it\delta}B_{r}\sim \partial {\it\Psi}/\partial {\it\theta}\sim m{\it\psi}/r$
and
 ${\it\Psi}_{0}^{\prime }\sim rB_{z}/Rq$
, so
${\it\Psi}_{0}^{\prime }\sim rB_{z}/Rq$
, so
 $$\begin{eqnarray}{\it\Delta}\sim 4\left(\frac{{\it\delta}B_{r}}{B_{z}q^{\prime }}\right)^{1/2}\left(\frac{q^{2}R}{m}\right)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\Delta}\sim 4\left(\frac{{\it\delta}B_{r}}{B_{z}q^{\prime }}\right)^{1/2}\left(\frac{q^{2}R}{m}\right)^{1/2}.\end{eqnarray}$$
Thus the island width is proportional to the square root of the
perturbing field, and inversely proportional to the square root of the shear
![]() $q^{\prime }$
.
$q^{\prime }$
.

Figure 11. Magnetic surfaces resulting from a helical perturbation with
(a)
![]() $m=3$
and (b)
$m=3$
and (b)
![]() $m=7$
.
$m=7$
.
3.1. Chaotic regions
We have seen that a single helical perturbation of circular surfaces produces islands
at a resonant surface, but these are still magnetic surfaces, albeit more complex
ones. This is because the perturbed system retains an ignorable coordinate
 $(m{\it\theta}+kz)$
. Note that this is true only of the straight helical system; it is
not true if we add a helical field to a torus (as in a toroidal
stellarator!).
$(m{\it\theta}+kz)$
. Note that this is true only of the straight helical system; it is
not true if we add a helical field to a torus (as in a toroidal
stellarator!).
When we impose two or more perturbations of different helical pitch there is no longer an ignorable coordinate (Rosenbluth et al. Reference Rosenbluth1966). If the amplitudes of the two perturbations are small, numerical computations show that each perturbation produces a separate chain of islands at its own resonant surface – but the interaction between them produces small chaotic regions near the X-points of each chain. As the perturbations increase, these chaotic regions expand to fill the space between the two chains.
This behaviour is illustrated in a plane slab model with two incommensurable Fourier perturbations (Wesson Reference Wesson2004). The fields in this model are
 $$\begin{eqnarray}\displaystyle & B_{z}=B_{0}=\text{constant}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{z}=B_{0}=\text{constant}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{x}=B_{x}^{\prime }y, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{x}=B_{x}^{\prime }y, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{y}={\it\delta}B_{y}[\cos (k_{z}z+k_{x}x)+\cos (k_{z}z-k_{x}x)], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{y}={\it\delta}B_{y}[\cos (k_{z}z+k_{x}x)+\cos (k_{z}z-k_{x}x)], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\frac{\text{d}x}{\text{d}z}=\frac{B_{x}}{B_{z}},\quad \frac{\text{d}y}{\text{d}z}=\frac{B_{y}}{B_{z}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}x}{\text{d}z}=\frac{B_{x}}{B_{z}},\quad \frac{\text{d}y}{\text{d}z}=\frac{B_{y}}{B_{z}}.\end{eqnarray}$$
The resulting Poincaré plots at fixed
![]() $z$
are shown in figure 12. As
each chaotic zone is generated by following a single field line,
plasma can readily flow throughout a chaotic zone. An interesting question is
therefore: What is the magnitude of the perturbations that cause the chaotic zones to
first extend from one island chain to the next? This can be estimated by calculating
the width of the islands in each chain, according to the formula given above, and
assuming that the last magnetic surface between island chains disappears when their
individual widths overlap. However, as we remarked earlier, an accurate calculation
is a fundamental problem in mathematical chaos theory.
$z$
are shown in figure 12. As
each chaotic zone is generated by following a single field line,
plasma can readily flow throughout a chaotic zone. An interesting question is
therefore: What is the magnitude of the perturbations that cause the chaotic zones to
first extend from one island chain to the next? This can be estimated by calculating
the width of the islands in each chain, according to the formula given above, and
assuming that the last magnetic surface between island chains disappears when their
individual widths overlap. However, as we remarked earlier, an accurate calculation
is a fundamental problem in mathematical chaos theory.

Figure 12. Illustration of the break-up of magnetic surfaces in the presence of
multiple perturbations with increasing strength: (a)
 ${\it\delta}B_{y}=0.1$
; (b)
${\it\delta}B_{y}=0.1$
; (b)
 ${\it\delta}B_{y}=0.2$
; (c)
${\it\delta}B_{y}=0.2$
; (c)
 ${\it\delta}B_{y}=0.3$
;(d)
${\it\delta}B_{y}=0.3$
;(d)
 ${\it\delta}B_{y}=1.0$
.
${\it\delta}B_{y}=1.0$
.
3.2. Mappings
One way to study chaotic break-up of surfaces is by numerical calculation of field lines and construction of the Poincaré plot as in the figures above. However, as field lines must be followed very accurately for many circuits of the torus, such calculations are lengthy. Therefore one often uses a simple ‘Iterative Mapping’ to illustrate the break-up of magnetic surfaces (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2010).
The mapping
 $$\begin{eqnarray}\displaystyle & x_{n+1}=\,f(x_{n},y_{n}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & x_{n+1}=\,f(x_{n},y_{n}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & y_{n+1}=g(x_{n},y_{n}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & y_{n+1}=g(x_{n},y_{n}), & \displaystyle\end{eqnarray}$$
In order to represent
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
, the mapping must be area-preserving. That is, any area must map
into an equal area. A general area-preserving map can be written implicitly in the
form
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0$
, the mapping must be area-preserving. That is, any area must map
into an equal area. A general area-preserving map can be written implicitly in the
form
 $$\begin{eqnarray}\displaystyle & \displaystyle x_{n+1}=x_{n}-\frac{\partial G}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle x_{n+1}=x_{n}-\frac{\partial G}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\theta}_{n+1}={\it\theta}_{n}+\frac{\partial G}{\partial x_{n+1}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\theta}_{n+1}={\it\theta}_{n}+\frac{\partial G}{\partial x_{n+1}}, & \displaystyle\end{eqnarray}$$
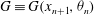 $G\equiv G(x_{n+1},{\it\theta}_{n})$
.
$G\equiv G(x_{n+1},{\it\theta}_{n})$
.
The simplest map that simulates the formation of magnetic islands and chaotic regions is the standard or Chirikov–Taylor map (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2010),
 $$\begin{eqnarray}\displaystyle & x_{n+1}=x_{n}+k\sin {\it\theta}_{n}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & x_{n+1}=x_{n}+k\sin {\it\theta}_{n}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\it\theta}_{n+1}={\it\theta}_{n}+x_{n}+k\sin {\it\theta}_{n}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\theta}_{n+1}={\it\theta}_{n}+x_{n}+k\sin {\it\theta}_{n}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}G(x_{n+1},{\it\theta}_{n})=\frac{x_{n+1}^{2}}{2}+k\cos {\it\theta}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}G(x_{n+1},{\it\theta}_{n})=\frac{x_{n+1}^{2}}{2}+k\cos {\it\theta}_{n}.\end{eqnarray}$$
The important features of this mapping are:
-
(i) it is periodic in
 ${\it\theta}$
, representing the poloidal angle;
${\it\theta}$
, representing the poloidal angle; -
(ii) when
 $k=0$
,
$k=0$
,
 $x_{n}=$
constant, representing the behaviour of a line of force
lying on a magnetic surface;
$x_{n}=$
constant, representing the behaviour of a line of force
lying on a magnetic surface; -
(iii) the difference
 $({\it\theta}_{n+1}-{\it\theta}_{n})$
represents the rotational transform
$({\it\theta}_{n+1}-{\it\theta}_{n})$
represents the rotational transform
 ${\it\iota}$
on a flux surface (note that this varies from one surface
to another); and
${\it\iota}$
on a flux surface (note that this varies from one surface
to another); and -
(iv) the term
 $k\sin {\it\theta}$
represents a perturbation of the magnetic field.
$k\sin {\it\theta}$
represents a perturbation of the magnetic field.
In a Poincaré plot generated by a continuous field line between
intersections of the Poincaré plane,
![]() $k\sin {\it\theta}$
would represent perturbation by a single helical mode. As we have
seen, a single helical perturbation does not create chaotic regions, but because the
mapping is discontinuous, the term
$k\sin {\it\theta}$
would represent perturbation by a single helical mode. As we have
seen, a single helical perturbation does not create chaotic regions, but because the
mapping is discontinuous, the term
![]() $k\sin {\it\theta}$
is equivalent to a discontinuous perturbation of the field
containing many helical modes.
$k\sin {\it\theta}$
is equivalent to a discontinuous perturbation of the field
containing many helical modes.
The results of iterating the standard map are shown in figure 13 for several values of the perturbation amplitude
![]() $k$
. As expected, when
$k$
. As expected, when
![]() $k$
is small, islands appear with small chaotic regions near X-points.
These chaotic regions expand, at the expense of continuous surfaces, as
$k$
is small, islands appear with small chaotic regions near X-points.
These chaotic regions expand, at the expense of continuous surfaces, as
![]() $k$
increases until the last continuous surface between island chains
disappears. By the overlap criterion above, this occurs at
$k$
increases until the last continuous surface between island chains
disappears. By the overlap criterion above, this occurs at
 $k_{c}\sim {\rm\pi}^{2}/4$
; the true value is 0.971635…(Greene Reference Greene1968; Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2010).
$k_{c}\sim {\rm\pi}^{2}/4$
; the true value is 0.971635…(Greene Reference Greene1968; Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2010).
4. Motion of lines of force
So far we have considered only stationary plasmas and fields. We now turn to some aspects of the motion of magnetic fields and plasmas. This depends on the time scale of the motion and the resistivity of the plasma. As expected, the key lies in Ohm’s law, which connects the magnetic field with the plasma motion and with resistivity.
4.1. Fluid model with resistivity
The resistive fluid model is described by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\it\rho}\frac{\text{d}\boldsymbol{v}}{\text{d}t}=\,\boldsymbol{j}\times \boldsymbol{B}-\boldsymbol{{\rm\nabla}}p,\\ \displaystyle \frac{1}{p}\frac{\text{d}p}{\text{d}t}=\frac{{\it\gamma}}{{\it\rho}}\frac{\text{d}{\it\rho}}{\text{d}t},\\ \displaystyle \frac{\partial {\it\rho}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0,\\ \boldsymbol{{\rm\nabla}}\times \boldsymbol{ B}={\it\mu}_{0}\,\boldsymbol{j},\\ \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{ B}=0,\\ \displaystyle \boldsymbol{{\rm\nabla}}\times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t},\\ \boldsymbol{ E}+\boldsymbol{ v}\times \boldsymbol{ B}={\it\eta}\,\boldsymbol{j},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\it\rho}\frac{\text{d}\boldsymbol{v}}{\text{d}t}=\,\boldsymbol{j}\times \boldsymbol{B}-\boldsymbol{{\rm\nabla}}p,\\ \displaystyle \frac{1}{p}\frac{\text{d}p}{\text{d}t}=\frac{{\it\gamma}}{{\it\rho}}\frac{\text{d}{\it\rho}}{\text{d}t},\\ \displaystyle \frac{\partial {\it\rho}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{v})=0,\\ \boldsymbol{{\rm\nabla}}\times \boldsymbol{ B}={\it\mu}_{0}\,\boldsymbol{j},\\ \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{ B}=0,\\ \displaystyle \boldsymbol{{\rm\nabla}}\times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t},\\ \boldsymbol{ E}+\boldsymbol{ v}\times \boldsymbol{ B}={\it\eta}\,\boldsymbol{j},\end{array}\right\}\end{eqnarray}$$
and the evolution of the field is given by
 $$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}^{2}\boldsymbol{B}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}^{2}\boldsymbol{B}.\end{eqnarray}$$
The two important time scales in a plasma can be seen in the
behaviour of small-amplitude waves, transverse to
![]() $\boldsymbol{B}_{0}$
in an incompressible plasma (Alfvén waves). Then
$\boldsymbol{B}_{0}$
in an incompressible plasma (Alfvén waves). Then
 $b\sim \exp (-\text{i}{\it\omega}t+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r})$
and (4.1) reduce
to
$b\sim \exp (-\text{i}{\it\omega}t+\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r})$
and (4.1) reduce
to
 $$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}{\it\omega}\boldsymbol{b}_{\bot }=\text{i}\boldsymbol{k}\times (\boldsymbol{v}_{\bot }\times \boldsymbol{B}_{0})+\frac{{\it\eta}}{{\it\mu}_{0}}\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{b}_{\bot })=\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})\boldsymbol{v}_{\bot }-\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\boldsymbol{b}_{\bot }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}{\it\omega}\boldsymbol{b}_{\bot }=\text{i}\boldsymbol{k}\times (\boldsymbol{v}_{\bot }\times \boldsymbol{B}_{0})+\frac{{\it\eta}}{{\it\mu}_{0}}\boldsymbol{k}\times (\boldsymbol{k}\times \boldsymbol{b}_{\bot })=\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})\boldsymbol{v}_{\bot }-\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\boldsymbol{b}_{\bot }, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}{\it\omega}{\it\rho}_{0}\boldsymbol{v}_{\bot }={\it\mu}_{0}^{-1}(\text{i}\boldsymbol{k}\times \boldsymbol{b}_{\bot })\times \boldsymbol{B}_{0}\approx \text{i}{\it\mu}_{0}^{-1}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})\boldsymbol{b}_{\bot }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}{\it\omega}{\it\rho}_{0}\boldsymbol{v}_{\bot }={\it\mu}_{0}^{-1}(\text{i}\boldsymbol{k}\times \boldsymbol{b}_{\bot })\times \boldsymbol{B}_{0}\approx \text{i}{\it\mu}_{0}^{-1}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})\boldsymbol{b}_{\bot }, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}{\it\omega}^{2}\boldsymbol{v}_{\bot }=\left[\frac{(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})^{2}}{{\it\mu}_{0}{\it\rho}_{0}}-\text{i}{\it\omega}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\right]\boldsymbol{v}_{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}^{2}\boldsymbol{v}_{\bot }=\left[\frac{(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0})^{2}}{{\it\mu}_{0}{\it\rho}_{0}}-\text{i}{\it\omega}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\right]\boldsymbol{v}_{\bot }.\end{eqnarray}$$
Equation (4.5)
defines the characteristic speed
 $v_{A}^{2}=B_{0}^{2}/{\it\mu}_{0}{\it\rho}_{0}$
of Alfvén waves, the Alfvén time scale
$v_{A}^{2}=B_{0}^{2}/{\it\mu}_{0}{\it\rho}_{0}$
of Alfvén waves, the Alfvén time scale
 ${\it\tau}_{A}^{2}\sim a^{2}{\it\mu}_{0}{\it\rho}_{0}/B_{0}^{2}$
and the resistive time scale of the wave damping
${\it\tau}_{A}^{2}\sim a^{2}{\it\mu}_{0}{\it\rho}_{0}/B_{0}^{2}$
and the resistive time scale of the wave damping
 ${\it\tau}_{R}\sim {\it\mu}_{0}a^{2}/{\it\eta}$
.
${\it\tau}_{R}\sim {\it\mu}_{0}a^{2}/{\it\eta}$
.
The ratio of the resistive to Alfvén time scales is the Lundquist number,
![]() $S$
,
$S$
,
 $$\begin{eqnarray}S=\frac{{\it\tau}_{R}}{{\it\tau}_{A}}\sim \frac{a^{2}}{{\it\eta}}\frac{B}{a\sqrt{{\it\mu}_{0}{\it\rho}}}.\end{eqnarray}$$
$$\begin{eqnarray}S=\frac{{\it\tau}_{R}}{{\it\tau}_{A}}\sim \frac{a^{2}}{{\it\eta}}\frac{B}{a\sqrt{{\it\mu}_{0}{\it\rho}}}.\end{eqnarray}$$
In high-temperature laboratory plasmas
 $S\sim 10^{6}{-}10^{8}$
(in astrophysical plasmas it is
$S\sim 10^{6}{-}10^{8}$
(in astrophysical plasmas it is
![]() ${\sim}10^{14}$
). These large values of
${\sim}10^{14}$
). These large values of
![]() $S$
create serious difficulties but can also lead to great
simplification. The difficulties lie in computing over such an enormous range of time
scales. The simplification is that field diffusion can often be ignored and the
resistivity set to zero. This leads to some crucial properties of an ideal plasma, or
of a real plasma on a time scale much less than
$S$
create serious difficulties but can also lead to great
simplification. The difficulties lie in computing over such an enormous range of time
scales. The simplification is that field diffusion can often be ignored and the
resistivity set to zero. This leads to some crucial properties of an ideal plasma, or
of a real plasma on a time scale much less than
![]() ${\it\tau}_{R}$
.
${\it\tau}_{R}$
.
(i) Flux conservation. The magnetic flux
 ${\it\phi}=\int _{S}\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{A}$
through an area
${\it\phi}=\int _{S}\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{A}$
through an area
![]() $S$
bounded by a closed curve
$S$
bounded by a closed curve
![]() $C$
that moves with the fluid is constant.
$C$
that moves with the fluid is constant.
The rate of change of the flux is
 $$\begin{eqnarray}\frac{\text{d}{\it\phi}}{\text{d}t}=\int \frac{\partial \boldsymbol{B}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{A}+\oint \boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{v}\times \text{d}\boldsymbol{l},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}{\it\phi}}{\text{d}t}=\int \frac{\partial \boldsymbol{B}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{A}+\oint \boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{v}\times \text{d}\boldsymbol{l},\end{eqnarray}$$
where the first term is due to the change in the field
![]() $\boldsymbol{B}$
and the second is due to motion of the boundary moving with the
fluid. The total change can be written as
$\boldsymbol{B}$
and the second is due to motion of the boundary moving with the
fluid. The total change can be written as
 $$\begin{eqnarray}\int \left[\frac{\partial \boldsymbol{B}}{\partial t}-\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})\right]\boldsymbol{\cdot }\text{d}\boldsymbol{A},\end{eqnarray}$$
$$\begin{eqnarray}\int \left[\frac{\partial \boldsymbol{B}}{\partial t}-\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})\right]\boldsymbol{\cdot }\text{d}\boldsymbol{A},\end{eqnarray}$$
which, by virtue of the field evolution equation (4.2), is always zero when
![]() ${\it\eta}=0$
.
${\it\eta}=0$
.
(ii) Field line preservation. A line moving with the fluid that is initially a line of force always remains a line of force. (Alternatively, if fluid particles initially lie on a common line of force then they continue to do so.)

Figure 14. Magnetic island formation.
To show this, it is convenient to reintroduce Clebsch variables as in § 2.1. Then
 $$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta},\end{eqnarray}$$
where
 ${\it\alpha}(x,y,t)$
and
${\it\alpha}(x,y,t)$
and
 ${\it\beta}(x,y,t)$
are constant along a line of force (crucially they label each line
of force). Therefore
${\it\beta}(x,y,t)$
are constant along a line of force (crucially they label each line
of force). Therefore
 $$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\left(\boldsymbol{{\rm\nabla}}\frac{\partial {\it\alpha}}{\partial t}\right)\times \boldsymbol{{\rm\nabla}}{\it\beta}-\left(\boldsymbol{{\rm\nabla}}\frac{\partial {\it\beta}}{\partial t}\right)\times \boldsymbol{{\rm\nabla}}{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\left(\boldsymbol{{\rm\nabla}}\frac{\partial {\it\alpha}}{\partial t}\right)\times \boldsymbol{{\rm\nabla}}{\it\beta}-\left(\boldsymbol{{\rm\nabla}}\frac{\partial {\it\beta}}{\partial t}\right)\times \boldsymbol{{\rm\nabla}}{\it\alpha}.\end{eqnarray}$$
However, we also have
 $$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{B}}{\partial t} & = & \displaystyle \boldsymbol{{\rm\nabla}}\times [\boldsymbol{v}\times (\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta})]\nonumber\\ \displaystyle & = & \displaystyle -\boldsymbol{{\rm\nabla}}\times [(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha})\boldsymbol{{\rm\nabla}}{\it\beta}-(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta})\boldsymbol{{\rm\nabla}}{\it\alpha}]\nonumber\\ \displaystyle & = & \displaystyle -\boldsymbol{{\rm\nabla}}(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha})\times \boldsymbol{{\rm\nabla}}{\it\beta}+\boldsymbol{{\rm\nabla}}(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta})\times \boldsymbol{{\rm\nabla}}{\it\alpha},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial \boldsymbol{B}}{\partial t} & = & \displaystyle \boldsymbol{{\rm\nabla}}\times [\boldsymbol{v}\times (\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta})]\nonumber\\ \displaystyle & = & \displaystyle -\boldsymbol{{\rm\nabla}}\times [(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha})\boldsymbol{{\rm\nabla}}{\it\beta}-(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta})\boldsymbol{{\rm\nabla}}{\it\alpha}]\nonumber\\ \displaystyle & = & \displaystyle -\boldsymbol{{\rm\nabla}}(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha})\times \boldsymbol{{\rm\nabla}}{\it\beta}+\boldsymbol{{\rm\nabla}}(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta})\times \boldsymbol{{\rm\nabla}}{\it\alpha},\end{eqnarray}$$
where
![]() $\boldsymbol{v}$
is the fluid velocity. Although (4.10) and (4.11) do not completely determine
$\boldsymbol{v}$
is the fluid velocity. Although (4.10) and (4.11) do not completely determine
![]() $\partial _{t}{\it\alpha}$
and
$\partial _{t}{\it\alpha}$
and
![]() $\partial _{t}{\it\beta}$
, a consistent solution is
$\partial _{t}{\it\beta}$
, a consistent solution is
 $$\begin{eqnarray}\frac{\partial {\it\alpha}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha}=0,\quad \frac{\partial {\it\beta}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial {\it\alpha}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha}=0,\quad \frac{\partial {\it\beta}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\beta}=0.\end{eqnarray}$$
That is to say, there is a labelling of the lines of force in a
moving ideal plasma such that each line moves with the fluid velocity
 $\boldsymbol{v}_{F}=\boldsymbol{E}\times \boldsymbol{B}/B^{2}$
. Because the field lines are locked into the fluid, they cannot
break or intersect one another, since this would require a discontinuous fluid
velocity.
$\boldsymbol{v}_{F}=\boldsymbol{E}\times \boldsymbol{B}/B^{2}$
. Because the field lines are locked into the fluid, they cannot
break or intersect one another, since this would require a discontinuous fluid
velocity.
Note that the choice of field line labels, and of their velocity, is not unique. In
fact, instead of saying that field lines move with the velocity of the fluid,
![]() $\boldsymbol{v}$
, we could equally say that they move with velocity
$\boldsymbol{v}$
, we could equally say that they move with velocity
![]() $(\boldsymbol{v}+\boldsymbol{u})$
, where
$(\boldsymbol{v}+\boldsymbol{u})$
, where
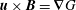 $\boldsymbol{u}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}G$
, and
$\boldsymbol{u}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}G$
, and
![]() $G$
is any function satisfying
$G$
is any function satisfying
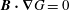 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}G=0$
. Of course, no physical quantity would be affected by this. It
would simply be a different labelling of the imaginary lines of force.
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}G=0$
. Of course, no physical quantity would be affected by this. It
would simply be a different labelling of the imaginary lines of force.
4.2. Effect of field line preservation
The effect of field line preservation in an ideal plasma can be seen if one tries to
calculate the growth of magnetic islands in the so-called ‘sheared slab’
configuration
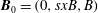 $\boldsymbol{B}_{0}=(0,sxB,B)$
, shown in figure 14. In this
configuration
$\boldsymbol{B}_{0}=(0,sxB,B)$
, shown in figure 14. In this
configuration
![]() $B_{y}$
varies only in the
$B_{y}$
varies only in the
![]() $x$
direction and changes sign at
$x$
direction and changes sign at
![]() $x=0$
. The question is: Can the field lines in this equilibrium reconnect
across the
$x=0$
. The question is: Can the field lines in this equilibrium reconnect
across the
![]() $x=0$
plane to form magnetic islands? This would occur if there were an
unstable perturbation with
$x=0$
plane to form magnetic islands? This would occur if there were an
unstable perturbation with
![]() $B_{x1}\neq 0$
at
$B_{x1}\neq 0$
at
![]() $x=0$
. For example, a single Fourier mode
$x=0$
. For example, a single Fourier mode
 ${\sim}\exp (\text{i}ky)$
could create a chain of islands like those in figure 14. (For such a mode, the ‘resonant surface’
${\sim}\exp (\text{i}ky)$
could create a chain of islands like those in figure 14. (For such a mode, the ‘resonant surface’
 $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
is located at
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
is located at
![]() $x=0$
.)
$x=0$
.)
A perturbation (
![]() $\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{1}$
,
![]() $\boldsymbol{v}_{1}$
) of the sheared slab equilibrium satisfies
$\boldsymbol{v}_{1}$
) of the sheared slab equilibrium satisfies
 $$\begin{eqnarray}\frac{\partial \boldsymbol{B}_{1}}{\partial t}=(\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{v}_{1}-(\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{B}_{0}-\boldsymbol{B}_{0}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1})\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}_{1}}{\partial t}=(\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{v}_{1}-(\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{B}_{0}-\boldsymbol{B}_{0}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1})\end{eqnarray}$$
and for the single Fourier mode
 $B_{1}\sim B_{1}(x)\exp (\text{i}ky)$
,
$B_{1}\sim B_{1}(x)\exp (\text{i}ky)$
,
 $$\begin{eqnarray}\frac{\partial B_{x1}}{\partial t}=(\text{i}skxB_{0})v_{x1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial B_{x1}}{\partial t}=(\text{i}skxB_{0})v_{x1}.\end{eqnarray}$$
We see from this that growth of a reconnecting field across the
![]() $x=0$
plane would require an infinite fluid velocity at
$x=0$
plane would require an infinite fluid velocity at
![]() $x=0$
if the plasma resistivity were precisely zero!
$x=0$
if the plasma resistivity were precisely zero!
5. Resistive plasmas
In a resistive plasma, field lines can break and reconnect. At first
sight we might expect this process to be slow, as it is in resistive diffusion. However,
reconnection occurs much more rapidly if it is concentrated in a small region
![]() ${\it\delta}\ll a$
. Then it occurs at a rate
${\it\delta}\ll a$
. Then it occurs at a rate
 ${\it\eta}/{\it\delta}^{2}\gg 1/{\it\tau}_{R}$
. An important example of this rapid reconnection occurs in resistive
instabilities.
${\it\eta}/{\it\delta}^{2}\gg 1/{\it\tau}_{R}$
. An important example of this rapid reconnection occurs in resistive
instabilities.
5.1. Resistive instabilities: the tearing mode
The basic ‘tearing mode’ instability involves the growth of magnetic islands in the
sheared slab that we considered in the previous section (Furth
et al.
Reference Furth, Killeen and Rosenbluth1963). As we found, if
![]() ${\it\eta}=0$
any such growth is prevented by the field line preservation
constraint, but now we wish to calculate the rate of growth when
${\it\eta}=0$
any such growth is prevented by the field line preservation
constraint, but now we wish to calculate the rate of growth when
![]() ${\it\eta}\neq 0$
. In particular, we are interested in instabilities that grow
rapidly compared to resistive diffusion, but slowly compared to MHD Alfvén time
scales.
${\it\eta}\neq 0$
. In particular, we are interested in instabilities that grow
rapidly compared to resistive diffusion, but slowly compared to MHD Alfvén time
scales.
We again start from a sheared slab equilibrium
![]() $\boldsymbol{v}=0$
and
$\boldsymbol{v}=0$
and
 $\boldsymbol{B}_{0}=(0,B_{0y}(sx),B_{0z})$
. We assume that
$\boldsymbol{B}_{0}=(0,B_{0y}(sx),B_{0z})$
. We assume that
![]() $B_{0y}(sx)$
is symmetric about
$B_{0y}(sx)$
is symmetric about
![]() $x=0$
and that the plasma is incompressible. Then the growth of a linear
perturbation (
$x=0$
and that the plasma is incompressible. Then the growth of a linear
perturbation (
![]() $\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{1}$
,
![]() $\boldsymbol{v}$
) is given by
$\boldsymbol{v}$
) is given by
 $$\begin{eqnarray}\frac{\partial \boldsymbol{B}_{1}}{\partial t}=\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}-\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{B}_{0}+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}^{2}\boldsymbol{B}_{1}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}_{1}}{\partial t}=\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}-\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{B}_{0}+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}^{2}\boldsymbol{B}_{1}\end{eqnarray}$$
and
 $$\begin{eqnarray}{\it\rho}_{0}\frac{\partial \boldsymbol{v}}{\partial t}=-\boldsymbol{{\rm\nabla}}p+\,\boldsymbol{j}_{1}\times \boldsymbol{B}_{0}+\,\boldsymbol{j}_{0}\times \boldsymbol{B}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\rho}_{0}\frac{\partial \boldsymbol{v}}{\partial t}=-\boldsymbol{{\rm\nabla}}p+\,\boldsymbol{j}_{1}\times \boldsymbol{B}_{0}+\,\boldsymbol{j}_{0}\times \boldsymbol{B}_{1}.\end{eqnarray}$$
It is convenient to write
 $\boldsymbol{B}_{1}=\hat{z}\times \boldsymbol{{\rm\nabla}}A_{1}$
. Then for a Fourier mode
$\boldsymbol{B}_{1}=\hat{z}\times \boldsymbol{{\rm\nabla}}A_{1}$
. Then for a Fourier mode
 $A\sim A_{1}(x)\exp ({\it\gamma}t+\text{i}ky)$
,
$A\sim A_{1}(x)\exp ({\it\gamma}t+\text{i}ky)$
,
 $B_{x1}=-\text{i}kA_{1}$
, and we can extract equations for (
$B_{x1}=-\text{i}kA_{1}$
, and we can extract equations for (
![]() $A_{1}$
,
$A_{1}$
,
![]() $v_{x}$
) alone, decoupled from all other components,
$v_{x}$
) alone, decoupled from all other components,
 $$\begin{eqnarray}-{\it\gamma}A_{1}-B_{0y}(sx)v_{x}B_{0}+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}_{\bot }^{2}A_{1}=0\end{eqnarray}$$
$$\begin{eqnarray}-{\it\gamma}A_{1}-B_{0y}(sx)v_{x}B_{0}+\frac{{\it\eta}}{{\it\mu}_{0}}{\rm\nabla}_{\bot }^{2}A_{1}=0\end{eqnarray}$$
and
 $$\begin{eqnarray}\frac{{\it\gamma}{\it\rho}_{0}}{k^{2}}{\rm\nabla}_{\bot }^{2}v_{x}-\frac{B_{0y}(sx)}{{\it\mu}_{0}}{\rm\nabla}_{\bot }^{2}A_{1}+\frac{\text{d}\,j_{0}}{\text{d}x}A_{1}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\gamma}{\it\rho}_{0}}{k^{2}}{\rm\nabla}_{\bot }^{2}v_{x}-\frac{B_{0y}(sx)}{{\it\mu}_{0}}{\rm\nabla}_{\bot }^{2}A_{1}+\frac{\text{d}\,j_{0}}{\text{d}x}A_{1}=0.\end{eqnarray}$$
We saw that, when
![]() ${\it\eta}=0$
, island growth requires
${\it\eta}=0$
, island growth requires
![]() $v_{x}\rightarrow \infty$
at
$v_{x}\rightarrow \infty$
at
![]() $x=0$
. Hence we expect the effect of resistivity to be most important
near
$x=0$
. Hence we expect the effect of resistivity to be most important
near
![]() $x=0$
. We therefore divide the calculation into a thin inner layer around
$x=0$
. We therefore divide the calculation into a thin inner layer around
![]() $x=0$
, of thickness
$x=0$
, of thickness
![]() ${\it\delta}$
, where resistivity is important, and two outer regions
${\it\delta}$
, where resistivity is important, and two outer regions
![]() $|x|>{\it\delta}$
, where resistivity can be neglected. A solution is then constructed
in each outer region and matched to the solution in the inner layer.
$|x|>{\it\delta}$
, where resistivity can be neglected. A solution is then constructed
in each outer region and matched to the solution in the inner layer.
Because we expect the tearing mode to grow slowly compared to the Alfvén time, we can neglect inertia in the outer regions. Then in these regions
 $$\begin{eqnarray}\frac{\text{d}^{2}A^{ext}}{\text{d}x^{2}}-k^{2}A^{ext}-\frac{{\it\mu}_{0}}{B_{0y}(sx)}\frac{\text{d}\,j_{0}}{\text{d}x}A^{ext}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}^{2}A^{ext}}{\text{d}x^{2}}-k^{2}A^{ext}-\frac{{\it\mu}_{0}}{B_{0y}(sx)}\frac{\text{d}\,j_{0}}{\text{d}x}A^{ext}=0.\end{eqnarray}$$
Note that this is exactly the equation for ideal plasma equilibrium in the outer regions – this equilibrium merely adjusts itself to the slowly changing inner solution.
We can integrate (5.5) inwards from
![]() $\pm$
infinity, or from the plasma boundaries, and adjust the (linear)
amplitude of the left and right solutions to be equal at
$\pm$
infinity, or from the plasma boundaries, and adjust the (linear)
amplitude of the left and right solutions to be equal at
![]() $x=0$
. Then in general we will find that there is a discontinuity in the
slope
$x=0$
. Then in general we will find that there is a discontinuity in the
slope
![]() $(\text{d}A/\text{d}x)$
between the left and right solutions at
$(\text{d}A/\text{d}x)$
between the left and right solutions at
![]() $x=0$
. We define this discontinuity as the ‘stability index’,
$x=0$
. We define this discontinuity as the ‘stability index’,
 $$\begin{eqnarray}{\it\Delta}^{\prime }\equiv \frac{1}{A(0)}\left[\left(\frac{\text{d}A}{\text{d}x}\right)_{\!+{\it\delta}}-\left(\frac{\text{d}A}{\text{d}x}\right)_{\!-{\it\delta}}\right].\end{eqnarray}$$
$$\begin{eqnarray}{\it\Delta}^{\prime }\equiv \frac{1}{A(0)}\left[\left(\frac{\text{d}A}{\text{d}x}\right)_{\!+{\it\delta}}-\left(\frac{\text{d}A}{\text{d}x}\right)_{\!-{\it\delta}}\right].\end{eqnarray}$$
This
![]() ${\it\Delta}^{\prime }$
is all we require from the outer solutions and we will see later
that
${\it\Delta}^{\prime }$
is all we require from the outer solutions and we will see later
that
![]() ${\it\Delta}^{\prime }>0$
implies instability.
${\it\Delta}^{\prime }>0$
implies instability.
We now need to find a solution in the inner region. In this region
![]() $x$
is small but
$x$
is small but
![]() $v_{x}$
and
$v_{x}$
and
![]() $A_{1}$
vary very rapidly with
$A_{1}$
vary very rapidly with
![]() $x$
. We can therefore neglect the last term in (5.4) as well as derivatives in the
$x$
. We can therefore neglect the last term in (5.4) as well as derivatives in the
![]() $y$
direction. Then, in the thin resistive inner layer, equations
(5.3) and (5.4) reduce to
$y$
direction. Then, in the thin resistive inner layer, equations
(5.3) and (5.4) reduce to
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}A}{\text{d}x^{2}}-\frac{{\it\gamma}{\it\mu}_{0}}{{\it\eta}}A-\frac{sB_{0}{\it\mu}_{0}}{{\it\eta}}xv_{x}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}A}{\text{d}x^{2}}-\frac{{\it\gamma}{\it\mu}_{0}}{{\it\eta}}A-\frac{sB_{0}{\it\mu}_{0}}{{\it\eta}}xv_{x}=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{{\it\gamma}{\it\rho}_{0}}{k^{2}}\frac{\text{d}^{2}v_{x}}{\text{d}x^{2}}-\frac{s^{2}B_{0}^{2}}{{\it\eta}}x^{2}v_{x}-\frac{sB_{0}{\it\gamma}}{{\it\eta}}xA=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{{\it\gamma}{\it\rho}_{0}}{k^{2}}\frac{\text{d}^{2}v_{x}}{\text{d}x^{2}}-\frac{s^{2}B_{0}^{2}}{{\it\eta}}x^{2}v_{x}-\frac{sB_{0}{\it\gamma}}{{\it\eta}}xA=0. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}{\it\delta}^{4}=\frac{{\it\eta}{\it\gamma}{\it\rho}_{0}}{s^{2}k^{2}B_{0}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}^{4}=\frac{{\it\eta}{\it\gamma}{\it\rho}_{0}}{s^{2}k^{2}B_{0}^{2}},\end{eqnarray}$$
so that the layer has unit width in
![]() ${\it\tau}$
. We also rescale the velocity by introducing
${\it\tau}$
. We also rescale the velocity by introducing
 $w=(sB_{0}{\it\delta}/{\it\gamma})v_{x}$
. Then the resistive layer equations become
$w=(sB_{0}{\it\delta}/{\it\gamma})v_{x}$
. Then the resistive layer equations become
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}w}{\text{d}{\it\tau}^{2}}-{\it\tau}^{2}w={\it\tau}A, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}w}{\text{d}{\it\tau}^{2}}-{\it\tau}^{2}w={\it\tau}A, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}A}{\text{d}{\it\tau}^{2}}=\frac{{\it\gamma}{\it\mu}_{0}{\it\delta}^{2}}{{\it\eta}}(A+{\it\tau}w). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{2}A}{\text{d}{\it\tau}^{2}}=\frac{{\it\gamma}{\it\mu}_{0}{\it\delta}^{2}}{{\it\eta}}(A+{\it\tau}w). & \displaystyle\end{eqnarray}$$
 ${\it\gamma}{\it\mu}_{0}{\it\delta}^{2}/{\it\eta}$
. Hence, when we match the change in
${\it\gamma}{\it\mu}_{0}{\it\delta}^{2}/{\it\eta}$
. Hence, when we match the change in
 $$\begin{eqnarray}{\it\Delta}^{\prime }=\frac{{\it\gamma}{\it\mu}_{0}{\it\delta}}{{\it\eta}}\times (\text{number of order unity}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\Delta}^{\prime }=\frac{{\it\gamma}{\it\mu}_{0}{\it\delta}}{{\it\eta}}\times (\text{number of order unity}).\end{eqnarray}$$
Therefore
![]() ${\it\Delta}^{\prime }=0$
is the stability threshold and, when
${\it\Delta}^{\prime }=0$
is the stability threshold and, when
![]() ${\it\Delta}^{\prime }>0$
,
${\it\Delta}^{\prime }>0$
,
 $$\begin{eqnarray}{\it\gamma}\sim \frac{{\it\eta}^{3/5}}{{\it\mu}_{0}^{4/5}}\left(\frac{skB_{0}}{{\it\rho}^{1/2}}\right)^{2/5}({\it\Delta}^{\prime })^{4/5}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\gamma}\sim \frac{{\it\eta}^{3/5}}{{\it\mu}_{0}^{4/5}}\left(\frac{skB_{0}}{{\it\rho}^{1/2}}\right)^{2/5}({\it\Delta}^{\prime })^{4/5}.\end{eqnarray}$$
In terms of Alfvén and resistive times,
 ${\it\tau}_{A}=a\sqrt{{\it\mu}_{0}{\it\rho}}/B_{0}$
and
${\it\tau}_{A}=a\sqrt{{\it\mu}_{0}{\it\rho}}/B_{0}$
and
 ${\it\tau}_{R}=a^{2}{\it\mu}_{0}/{\it\eta}$
, defined relative to a characteristic dimension
${\it\tau}_{R}=a^{2}{\it\mu}_{0}/{\it\eta}$
, defined relative to a characteristic dimension
![]() $a$
of the outer plasma, equation (5.13) becomes
$a$
of the outer plasma, equation (5.13) becomes
 $$\begin{eqnarray}{\it\gamma}\sim \frac{(a{\it\Delta}^{\prime })^{4/5}(ka)^{2/5}(sa)^{2/5}}{{\it\tau}_{R}^{3/5}{\it\tau}_{A}^{2/5}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\gamma}\sim \frac{(a{\it\Delta}^{\prime })^{4/5}(ka)^{2/5}(sa)^{2/5}}{{\it\tau}_{R}^{3/5}{\it\tau}_{A}^{2/5}}.\end{eqnarray}$$
Consequently
 ${\it\gamma}{\it\tau}_{R}\sim S^{2/5}\gg 1$
and
${\it\gamma}{\it\tau}_{R}\sim S^{2/5}\gg 1$
and
 ${\it\gamma}{\it\tau}_{A}\sim S^{-3/5}\ll 1$
. So our assumptions about the tearing mode are confirmed: when
resistivity is small, the growth rate is indeed rapid compared to resistive diffusion
but slow compared to the Alfvén speed, and the resistive layer is thin, with the
width
${\it\gamma}{\it\tau}_{A}\sim S^{-3/5}\ll 1$
. So our assumptions about the tearing mode are confirmed: when
resistivity is small, the growth rate is indeed rapid compared to resistive diffusion
but slow compared to the Alfvén speed, and the resistive layer is thin, with the
width
![]() ${\it\delta}$
given by (5.9).
Note that in the limit
${\it\delta}$
given by (5.9).
Note that in the limit
![]() ${\it\eta}\rightarrow 0$
we recover an ideal plasma, but with a discontinuity in the form of
a current sheet at the resonant layer
${\it\eta}\rightarrow 0$
we recover an ideal plasma, but with a discontinuity in the form of
a current sheet at the resonant layer
 $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
– a possibility we did not consider in our discussion of ideal
plasmas.
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
– a possibility we did not consider in our discussion of ideal
plasmas.
It is important to recognise the significance of tearing modes. Of course, we expect that introducing a small resistivity will perturb the motion of a previously ideal plasma. But this is not what tearing modes do. Tearing modes are new modes involving critical layers in which resistivity is dominant no matter how small it may be. Mathematically they arise because the differential equations governing resistive plasma are of higher order than those governing ideal plasma. This means that there are solutions for the resistive plasma that do not exist when resistivity is strictly zero. (This is very similar to the effect of viscosity in fluid dynamics, where it also introduces additional solutions and is dominant in critical boundary layers.)
In addition to its intrinsic interest, there are several reasons why the calculation of tearing modes is important: (a) it describes an instability that has been seen in experiments, (b) it illustrates the importance of small departures from ideal Ohm’s law, (c) it confirms that reconnection can occur much faster than resistive diffusion and (d) the matching procedure described in the calculation is used in many other calculations when there is a small departure from the ideal plasma. In these calculations more complicated models are used in the resonant layer, but the outer region calculation is essentially unchanged.
In one respect, however, our calculation of the tearing mode growth rate is atypical. Recall that in the outer region
 $$\begin{eqnarray}\frac{\text{d}^{2}A}{\text{d}x^{2}}-k^{2}A=\frac{{\it\mu}_{0}}{B_{0y}(sx)}\frac{\text{d}\,j_{0}}{\text{d}x}A.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}^{2}A}{\text{d}x^{2}}-k^{2}A=\frac{{\it\mu}_{0}}{B_{0y}(sx)}\frac{\text{d}\,j_{0}}{\text{d}x}A.\end{eqnarray}$$
We assumed that
![]() $j_{0}$
was symmetric about
$j_{0}$
was symmetric about
![]() $x=0$
, so the right-hand side of this equation tends to a constant times
$x=0$
, so the right-hand side of this equation tends to a constant times
![]() $A$
as
$A$
as
![]() $x\rightarrow 0$
and the general solution near
$x\rightarrow 0$
and the general solution near
![]() $x=0$
is
$x=0$
is
 $$\begin{eqnarray}A\sim {\it\alpha}[1+\cdots \,]+{\it\beta}[x+\cdots \,].\end{eqnarray}$$
$$\begin{eqnarray}A\sim {\it\alpha}[1+\cdots \,]+{\it\beta}[x+\cdots \,].\end{eqnarray}$$
In this case
![]() $\text{d}A/\text{d}x$
and
$\text{d}A/\text{d}x$
and
![]() $A$
are well behaved at
$A$
are well behaved at
![]() $x=0$
and there is no difficulty in calculating
$x=0$
and there is no difficulty in calculating
![]() ${\it\Delta}^{\prime }$
. But if
${\it\Delta}^{\prime }$
. But if
![]() $j_{0}$
is not symmetric about
$j_{0}$
is not symmetric about
![]() $x=0$
, the right-hand side of the equation
$x=0$
, the right-hand side of the equation
![]() ${\sim}A/x$
as
${\sim}A/x$
as
![]() $x\rightarrow 0$
. Then the general solution near
$x\rightarrow 0$
. Then the general solution near
![]() $x=0$
is
$x=0$
is
 $$\begin{eqnarray}A\sim {\it\alpha}[1+c(x\log |x|-x)]+{\it\beta}[x+\cdots \,],\end{eqnarray}$$
$$\begin{eqnarray}A\sim {\it\alpha}[1+c(x\log |x|-x)]+{\it\beta}[x+\cdots \,],\end{eqnarray}$$
so that
![]() $A$
and
$A$
and
![]() $\text{d}A/\text{d}x$
are divergent at
$\text{d}A/\text{d}x$
are divergent at
![]() $x=0$
. In this case, rather than matching the derivatives of inner and
outer solutions, we match the large (
$x=0$
. In this case, rather than matching the derivatives of inner and
outer solutions, we match the large (
![]() ${\it\alpha}$
) and small (
${\it\alpha}$
) and small (
![]() ${\it\beta}$
) solutions in the inner and outer regions. (If we had included
plasma pressure in our calculation, the general solution would have been of the form
${\it\beta}$
) solutions in the inner and outer regions. (If we had included
plasma pressure in our calculation, the general solution would have been of the form
 ${\it\alpha}|x|^{q}+{\it\beta}|x|^{1-q}$
near
${\it\alpha}|x|^{q}+{\it\beta}|x|^{1-q}$
near
![]() $x=0$
, but we again match the large and small solutions.)
$x=0$
, but we again match the large and small solutions.)
One might reasonably question whether at this level of detail the plasma can really
be represented by a fluid model. However, the underlying concept of reconnection
occurring in a thin layer, but dependent on a parameter
![]() ${\it\Delta}^{\prime }$
calculated from the plasma outside this layer, appears to be
robust. This view is reinforced by another interpretation of
${\it\Delta}^{\prime }$
calculated from the plasma outside this layer, appears to be
robust. This view is reinforced by another interpretation of
![]() ${\it\Delta}^{\prime }$
. Suppose we remove the resistive layer and replace it by a thin
flexible insulating membrane. The magnetic pressure on this membrane is
${\it\Delta}^{\prime }$
. Suppose we remove the resistive layer and replace it by a thin
flexible insulating membrane. The magnetic pressure on this membrane is
![]() $B^{2}/2{\it\mu}_{0}$
, so if we deform it by a tearing-mode-like displacement
$B^{2}/2{\it\mu}_{0}$
, so if we deform it by a tearing-mode-like displacement
![]() ${\it\xi}_{x}$
, the work done by the plasma (per unit area) on one side of the
membrane is
${\it\xi}_{x}$
, the work done by the plasma (per unit area) on one side of the
membrane is
 $$\begin{eqnarray}{\it\delta}W\sim {\it\xi}_{x}\left(\frac{B_{0}^{2}}{2}+\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{1}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W\sim {\it\xi}_{x}\left(\frac{B_{0}^{2}}{2}+\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{1}\right).\end{eqnarray}$$
As there is no change of plasma volume, the contribution from
![]() $B_{0}^{2}$
is zero, and from the earlier calculation of tearing modes, in the
ideal plasma
$B_{0}^{2}$
is zero, and from the earlier calculation of tearing modes, in the
ideal plasma
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{1}=B_{0y}(sx)\frac{\partial A}{\partial x}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{1}=B_{0y}(sx)\frac{\partial A}{\partial x}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\it\xi}_{x}B_{0y}(sx)=-A, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\xi}_{x}B_{0y}(sx)=-A, & \displaystyle\end{eqnarray}$$
 ${\it\gamma}{\it\xi}_{x}=v_{x}$
. Therefore the net change of energy is
${\it\gamma}{\it\xi}_{x}=v_{x}$
. Therefore the net change of energy is  $$\begin{eqnarray}{\it\delta}W\sim A(0)^{2}\left[\left(\frac{1}{A}\frac{\text{d}A}{\text{d}x}\right)_{\!-{\it\varepsilon}}-\left(\frac{1}{A}\frac{\text{d}A}{\text{d}x}\right)_{\!{\it\varepsilon}}\right].\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W\sim A(0)^{2}\left[\left(\frac{1}{A}\frac{\text{d}A}{\text{d}x}\right)_{\!-{\it\varepsilon}}-\left(\frac{1}{A}\frac{\text{d}A}{\text{d}x}\right)_{\!{\it\varepsilon}}\right].\end{eqnarray}$$
Hence
![]() ${\it\Delta}^{\prime }$
is a measure of the energy available in the ideal plasma if the
field line conservation constraint is relaxed at the resonant surface
${\it\Delta}^{\prime }$
is a measure of the energy available in the ideal plasma if the
field line conservation constraint is relaxed at the resonant surface
 $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
.
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B}_{0}=0$
.
5.2. Forced reconnection
As we saw, tearing mode reconnection is driven by the energy released from an
unstable plasma. However, reconnection may occur even more rapidly when it is
‘forced’, that is, driven by plasma flows or imposed on the reconnecting region.
Conceptually we might view the forcing as being applied externally, as in
figure 15, effectively increasing the value
of
![]() ${\it\Delta}^{\prime }$
. In practice we will be more interested in reconnection driven by
turbulence.
${\it\Delta}^{\prime }$
. In practice we will be more interested in reconnection driven by
turbulence.

Figure 15. Faster reconnection:
![]() $P$
represents the forcing perturbation at the wall.
$P$
represents the forcing perturbation at the wall.
An often quoted idealised form of forced reconnection is the Sweet–Parker model. This
represents plasma flow through an X-point of a two-dimensional magnetic field, as
illustrated in figure 16. The antiparallel
reconnecting fields are forced towards the X-point by flows in the
![]() $\pm x$
direction, reconnect, and then flow outwards along the
$\pm x$
direction, reconnect, and then flow outwards along the
![]() $\pm y$
directions. We can readily imagine that the forced inflows cause
‘flattening’ of the X-point to eventually form a current sheet of thickness
$\pm y$
directions. We can readily imagine that the forced inflows cause
‘flattening’ of the X-point to eventually form a current sheet of thickness
![]() ${\it\delta}$
and length
${\it\delta}$
and length
![]() $l$
, as indicated in figure 16,
across which the field
$l$
, as indicated in figure 16,
across which the field
![]() $B$
changes direction. We can then envisage a steady state, with plasma
forced into the current sheet across the field, at a velocity
$B$
changes direction. We can then envisage a steady state, with plasma
forced into the current sheet across the field, at a velocity
![]() $v_{x,in}$
controlled by resistivity, and flowing out along the field at a
much higher velocity,
$v_{x,in}$
controlled by resistivity, and flowing out along the field at a
much higher velocity,
![]() $v_{y,out}$
.
$v_{y,out}$
.

Figure 16. Model of forced reconnection.
From Ohm’s law we have for the inflow,
 $v_{in}\sim {\it\eta}/{\it\delta}{\it\mu}_{0}$
. Pressure balance,
$v_{in}\sim {\it\eta}/{\it\delta}{\it\mu}_{0}$
. Pressure balance,
 ${\it\rho}v_{y}^{2}/2=B_{0}^{2}/2{\it\mu}_{0}$
, gives for the outflow,
${\it\rho}v_{y}^{2}/2=B_{0}^{2}/2{\it\mu}_{0}$
, gives for the outflow,
 $v_{out}\sim B/\sqrt{{\it\mu}_{0}{\it\rho}}$
, and mass conservation requires that
$v_{out}\sim B/\sqrt{{\it\mu}_{0}{\it\rho}}$
, and mass conservation requires that
 $v_{out}{\it\delta}\sim v_{in}l$
. Consequently,
$v_{out}{\it\delta}\sim v_{in}l$
. Consequently,
 $v_{in}^{2}\sim l^{2}/({\it\tau}_{R}{\it\tau}_{A})$
so that flux is swept in, and reconnects at a rate
$v_{in}^{2}\sim l^{2}/({\it\tau}_{R}{\it\tau}_{A})$
so that flux is swept in, and reconnects at a rate
 ${\sim}({\it\tau}_{A}{\it\tau}_{R})^{-1/2}$
, where
${\sim}({\it\tau}_{A}{\it\tau}_{R})^{-1/2}$
, where
![]() ${\it\tau}_{A}$
and
${\it\tau}_{A}$
and
![]() ${\it\tau}_{R}$
are again the Alfvén and resistive diffusion times relative to the
outer dimensions of the reconnecting region (with scale length
${\it\tau}_{R}$
are again the Alfvén and resistive diffusion times relative to the
outer dimensions of the reconnecting region (with scale length
![]() ${\sim}l$
).
${\sim}l$
).
Of course, both the tearing mode and the Sweet–Parker model are over-idealised and, except in carefully controlled experiments, can scarcely represent real situations. In particular, the strictly two-dimensional nature of these models is likely to be unrepresentative, and the Sweet–Parker outflow is also likely to be unstable. (Numerical simulations generally show that reconnection is faster than it is in the idealised models.)
In a turbulent plasma, a more realistic picture is one in which elements of plasma, carrying differently oriented frozen-in fields, are forced together. In the absence of reconnection, they could not penetrate each other and a current layer would form between them. However, resistivity allows some penetration and reconnection. If this is not fast enough to keep up with the inflow, magnetic field will pile up against the current sheet, making the Alfvén speed larger and the current sheet thinner, so that reconnection speeds up. Consequently, in a turbulent resistive plasma, we can expect reconnection to proceed freely.
6. Conclusion
In Part I we have introduced some important basic features of magnetised plasmas,
including the strong anisotropy (short range of effects in the direction perpendicular
to
![]() $\boldsymbol{B}$
, long range parallel to
$\boldsymbol{B}$
, long range parallel to
![]() $\boldsymbol{B}$
) and the consequent importance of magnetic field lines and surfaces.
Their most important properties are:
$\boldsymbol{B}$
) and the consequent importance of magnetic field lines and surfaces.
Their most important properties are:
-
(i) In an ideal
 $({\it\eta}=0)$
plasma, there are many constraints on their motion arising
from the fact that field lines cannot break or reconnect – even though they are
hypothetical! These constraints dominate the behaviour of ideal plasmas.
$({\it\eta}=0)$
plasma, there are many constraints on their motion arising
from the fact that field lines cannot break or reconnect – even though they are
hypothetical! These constraints dominate the behaviour of ideal plasmas. -
(ii) In an even slightly resistive plasma these constraints may be ineffective, leading to new phenomena (as well as small modifications of the ideal behaviour). In turbulent resistive plasmas we expect breaking and reconnection of field lines to be the rule rather than the exception, and, as we will see in Part II, this provides an explanation and a prediction of the behaviour of turbulent plasmas in a very wide range of experiments.
Part II
7. Plasma relaxation
Plasma relaxation theory (Taylor Reference Taylor1974b
, Reference Taylor1975, Reference Taylor1986, Reference Taylor2000) has its origin in early
experiments on toroidal pinches – notably ZETA (Butt et al.
Reference Butt, Cole, Dellis and Wort1966; Gibson et al.
Reference Gibson, Coxell, Powell and Reid1967). In these early pinch experiments, a
toroidal field
![]() $B_{0}$
is first created by external coils and a toroidal current
$B_{0}$
is first created by external coils and a toroidal current
![]() $I$
is then induced in the plasma (essentially by a transformer in which
the plasma torus is the secondary). This current rapidly heats and compresses the
plasma. A remarkable feature of these experiments is that, after an initial, violently
turbulent phase, the plasma enters a ‘quiescent’ phase in which the turbulence is much
reduced. Even more remarkable is the fact that in the quiescent phase the plasma profile
is almost independent of any details of the initial state and depends principally on the
‘pinch ratio’
$I$
is then induced in the plasma (essentially by a transformer in which
the plasma torus is the secondary). This current rapidly heats and compresses the
plasma. A remarkable feature of these experiments is that, after an initial, violently
turbulent phase, the plasma enters a ‘quiescent’ phase in which the turbulence is much
reduced. Even more remarkable is the fact that in the quiescent phase the plasma profile
is almost independent of any details of the initial state and depends principally on the
‘pinch ratio’
 ${\it\theta}=B_{{\it\theta}}/B_{0}$
, where
${\it\theta}=B_{{\it\theta}}/B_{0}$
, where
![]() $B_{{\it\theta}}$
is the poloidal field at the plasma boundary. (Alternatively,
$B_{{\it\theta}}$
is the poloidal field at the plasma boundary. (Alternatively,
 ${\it\theta}=2I/aB_{0}$
, where
${\it\theta}=2I/aB_{0}$
, where
![]() $a$
is the torus minor radius.) Furthermore, when
$a$
is the torus minor radius.) Furthermore, when
![]() ${\it\theta}$
exceeds a critical value, which is the same for all quiescent states,
the toroidal field in the outer plasma is spontaneously reversed relative to
the initial applied field!
${\it\theta}$
exceeds a critical value, which is the same for all quiescent states,
the toroidal field in the outer plasma is spontaneously reversed relative to
the initial applied field!
These observations suggest that the plasma has reached some preferred, possibly stable,
state – now known as the ‘relaxed state’. The idea of such a state can be illustrated by
a simple analogy. Suppose we immerse a flexible current-carrying loop of wire in a
viscous insulating medium. What is its equilibrium state? While the wire is moving, it
loses energy to the viscous medium, so its equilibrium must be a state of minimum energy
– but minimum energy subject to certain constraints. (Otherwise all the energy would be
dissipated!) One constraint is that the flux
![]() $LI$
linking the loop (
$LI$
linking the loop (
![]() $L$
is the inductance) is constant, and if this were the only constraint
the equilibrium would be the configuration of minimum
$L$
is the inductance) is constant, and if this were the only constraint
the equilibrium would be the configuration of minimum
![]() $LI^{2}/2$
, subject to
$LI^{2}/2$
, subject to
![]() $LI$
being constant. (This is the state of maximum inductance.)
$LI$
being constant. (This is the state of maximum inductance.)
A plasma resembles an infinity of linked flexible wires and the first problem is to identify the appropriate constraints (Taylor Reference Taylor1986).
7.1. Relaxation constraints
We have seen that, for a perfectly conducting plasma, important constraints follow from
 $$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B}),\end{eqnarray}$$
which we now write as
 $$\begin{eqnarray}\frac{\partial \boldsymbol{A}}{\partial t}=\boldsymbol{v}\times \boldsymbol{B}+\boldsymbol{{\rm\nabla}}{\it\chi},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \boldsymbol{A}}{\partial t}=\boldsymbol{v}\times \boldsymbol{B}+\boldsymbol{{\rm\nabla}}{\it\chi},\end{eqnarray}$$
where
![]() $\boldsymbol{A}$
is the vector potential and
$\boldsymbol{A}$
is the vector potential and
![]() ${\it\chi}$
is an arbitrary scalar. Consequently, changes in
${\it\chi}$
is an arbitrary scalar. Consequently, changes in
![]() $\boldsymbol{A}$
must satisfy a similar equation,
$\boldsymbol{A}$
must satisfy a similar equation,
 $$\begin{eqnarray}{\it\delta}\boldsymbol{A}={\bf\xi}\times \boldsymbol{B}+\boldsymbol{{\rm\nabla}}\overline{{\it\chi}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\boldsymbol{A}={\bf\xi}\times \boldsymbol{B}+\boldsymbol{{\rm\nabla}}\overline{{\it\chi}},\end{eqnarray}$$
where
![]() ${\bf\xi}$
is an arbitrary plasma displacement (and
${\bf\xi}$
is an arbitrary plasma displacement (and
![]() $\overline{{\it\chi}}$
follows from
$\overline{{\it\chi}}$
follows from
![]() ${\it\chi}$
). It is clear that this does not restrict
${\it\chi}$
). It is clear that this does not restrict
![]() ${\it\delta}\boldsymbol{A}_{\bot }$
, but
${\it\delta}\boldsymbol{A}_{\bot }$
, but
![]() ${\it\delta}A_{\Vert }$
is constrained by
${\it\delta}A_{\Vert }$
is constrained by
 $$\begin{eqnarray}\oint \frac{\text{d}l}{B}\;\boldsymbol{B}\boldsymbol{\cdot }{\it\delta}\boldsymbol{A}=0,\end{eqnarray}$$
$$\begin{eqnarray}\oint \frac{\text{d}l}{B}\;\boldsymbol{B}\boldsymbol{\cdot }{\it\delta}\boldsymbol{A}=0,\end{eqnarray}$$
for any closed field line or magnetic surface (see § 2.1).
A more convenient, and more fundamental, form of this constraint is that, for every
infinitesimal flux tube surrounding a closed field line labelled by Clebsch variables
![]() ${\it\alpha}$
,
${\it\alpha}$
,
![]() ${\it\beta}$
, and for every magnetic flux surface, the volume integral
${\it\beta}$
, and for every magnetic flux surface, the volume integral
 $$\begin{eqnarray}K_{{\it\alpha}{\it\beta}}\equiv \int _{{\it\alpha},{\it\beta}}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}\end{eqnarray}$$
$$\begin{eqnarray}K_{{\it\alpha}{\it\beta}}\equiv \int _{{\it\alpha},{\it\beta}}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}\end{eqnarray}$$
is invariant. This provides an infinity of constraints – which replace the single constraint of the flexible wire.
We can confirm the invariance of
![]() $K_{{\it\alpha}{\it\beta}}$
directly:
$K_{{\it\alpha}{\it\beta}}$
directly:
 $$\begin{eqnarray}\frac{\text{d}K_{{\it\alpha}{\it\beta}}}{\text{d}t}=\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\frac{\partial \boldsymbol{A}}{\partial t}\;\text{d}{\it\tau}+\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\frac{\partial \boldsymbol{B}}{\partial t}\;\text{d}{\it\tau}+\oint _{S}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K_{{\it\alpha}{\it\beta}}}{\text{d}t}=\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\frac{\partial \boldsymbol{A}}{\partial t}\;\text{d}{\it\tau}+\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\frac{\partial \boldsymbol{B}}{\partial t}\;\text{d}{\it\tau}+\oint _{S}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S},\end{eqnarray}$$
where
![]() $V$
and
$V$
and
![]() $S$
are respectively the volume and surface area of the infinitesimal
flux tube. The last term arises from the motion of the flux tube and the others from
the local change in
$S$
are respectively the volume and surface area of the infinitesimal
flux tube. The last term arises from the motion of the flux tube and the others from
the local change in
![]() $(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})$
. Then, from (7.2),
$(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})$
. Then, from (7.2),
 $$\begin{eqnarray}\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\frac{\partial \boldsymbol{A}}{\partial t}\;\text{d}{\it\tau}=\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\chi}\;\text{d}{\it\tau}=\oint _{S}{\it\chi}\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\frac{\partial \boldsymbol{A}}{\partial t}\;\text{d}{\it\tau}=\int _{V}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\chi}\;\text{d}{\it\tau}=\oint _{S}{\it\chi}\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
and from (7.1),
 $$\begin{eqnarray}\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\frac{\partial \boldsymbol{B}}{\partial t}\;\text{d}{\it\tau}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})\;\text{d}{\it\tau}=-\oint _{S}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})\,\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\frac{\partial \boldsymbol{B}}{\partial t}\;\text{d}{\it\tau}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}\times \boldsymbol{B})\;\text{d}{\it\tau}=-\oint _{S}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})\,\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}=0,\end{eqnarray}$$
(recall that
![]() $\boldsymbol{v}$
is tangential to the boundary
$\boldsymbol{v}$
is tangential to the boundary
![]() $S$
).
$S$
).
Hence
 $\text{d}K/\text{d}t=0$
, and to find the relaxed state we need to minimise the magnetic
energy
$\text{d}K/\text{d}t=0$
, and to find the relaxed state we need to minimise the magnetic
energy
 $\int _{V}\text{d}{\it\tau}\,B^{2}/2{\it\mu}_{0}$
over all variations
$\int _{V}\text{d}{\it\tau}\,B^{2}/2{\it\mu}_{0}$
over all variations
![]() ${\it\delta}\boldsymbol{A}$
subject to the infinity of constraints
${\it\delta}\boldsymbol{A}$
subject to the infinity of constraints
 $K_{{\it\alpha}{\it\beta}}=\text{constant}$
. This leads to the variational problem
$K_{{\it\alpha}{\it\beta}}=\text{constant}$
. This leads to the variational problem
 $$\begin{eqnarray}{\it\delta}\int _{V}\text{d}{\it\tau}\left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}-{\it\lambda}_{{\it\alpha},{\it\beta}}\,\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\right]_{all\,{\it\delta}\boldsymbol{A},\,{\it\delta}{\it\lambda}}=0.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\int _{V}\text{d}{\it\tau}\left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}-{\it\lambda}_{{\it\alpha},{\it\beta}}\,\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\right]_{all\,{\it\delta}\boldsymbol{A},\,{\it\delta}{\it\lambda}}=0.\end{eqnarray}$$
This is very inconvenient because of the restriction (
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=0$
) on
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=0$
) on
![]() ${\it\lambda}$
that is implicit in the use of Clebsch variables
${\it\lambda}$
that is implicit in the use of Clebsch variables
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
. We can avoid this by introducing the restriction explicitly
through another Lagrange multiplier. Then the variational problem becomes
${\it\beta}$
. We can avoid this by introducing the restriction explicitly
through another Lagrange multiplier. Then the variational problem becomes
 $$\begin{eqnarray}{\it\delta}\int _{V}\text{d}{\it\tau}\left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}-{\it\lambda}_{(x,y,z)}\,\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}+{\it\mu}_{(x,y,z)}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}\right]_{all\,{\it\delta}\boldsymbol{A},\,{\it\delta}{\it\lambda},\,{\it\delta}{\it\mu}}=0.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\int _{V}\text{d}{\it\tau}\left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}-{\it\lambda}_{(x,y,z)}\,\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}+{\it\mu}_{(x,y,z)}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}\right]_{all\,{\it\delta}\boldsymbol{A},\,{\it\delta}{\it\lambda},\,{\it\delta}{\it\mu}}=0.\end{eqnarray}$$
We also need to consider the appropriate boundary condition. When the magnetic field
is entirely contained within a closed conducting shell, the tangential component of
![]() ${\it\delta}\boldsymbol{A}$
on the boundary is zero.
${\it\delta}\boldsymbol{A}$
on the boundary is zero.
Returning to the variational problem, the minimisation requires
 $$\begin{eqnarray}\displaystyle {\it\delta}W={\it\delta}\boldsymbol{A}\boldsymbol{\cdot }\{\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-2{\it\lambda}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}-\boldsymbol{{\rm\nabla}}{\it\lambda}\times (\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W={\it\delta}\boldsymbol{A}\boldsymbol{\cdot }\{\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-2{\it\lambda}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}-\boldsymbol{{\rm\nabla}}{\it\lambda}\times (\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\} & = & \displaystyle 0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle -{\it\delta}{\it\lambda}\{(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})\boldsymbol{\cdot }(\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\} & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -{\it\delta}{\it\lambda}\{(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})\boldsymbol{\cdot }(\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\} & = & \displaystyle 0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle +{\it\delta}{\it\mu}\{(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}\} & = & \displaystyle 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle +{\it\delta}{\it\mu}\{(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}\} & = & \displaystyle 0.\end{eqnarray}$$
 $$\begin{eqnarray}(\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})={\bf\xi}\times \boldsymbol{B},\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})={\bf\xi}\times \boldsymbol{B},\end{eqnarray}$$
therefore
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}{\it\lambda}\times (\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\rightarrow (\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}){\bf\xi}-({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda})\boldsymbol{B},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}{\it\lambda}\times (\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\mu})\rightarrow (\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}){\bf\xi}-({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda})\boldsymbol{B},\end{eqnarray}$$
where the first term is zero. Then (7.11) becomes
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-(2{\it\lambda}-{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda})\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}=0.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-(2{\it\lambda}-{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda})\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}=0.\end{eqnarray}$$
Redefining
![]() ${\it\lambda}$
, we obtain finally
${\it\lambda}$
, we obtain finally
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}-{\it\lambda}_{{\it\alpha}{\it\beta}}\boldsymbol{B}=0.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}-{\it\lambda}_{{\it\alpha}{\it\beta}}\boldsymbol{B}=0.\end{eqnarray}$$
Now, note well, this cannot be the correct description of the
quiescent state, because
![]() ${\it\lambda}_{{\it\alpha}{\it\beta}}$
must be determined from the infinity of
${\it\lambda}_{{\it\alpha}{\it\beta}}$
must be determined from the infinity of
![]() $K_{{\it\alpha}{\it\beta}}$
, which in turn will reflect every detail of the initial conditions
– entirely contrary to the observations.
$K_{{\it\alpha}{\it\beta}}$
, which in turn will reflect every detail of the initial conditions
– entirely contrary to the observations.
The resolution of this dilemma is to recognise, as we did earlier, that even small
resistivity leads to field line breaking and reconnection. Then it is impossible to
identify individual field lines and the individual
![]() $K_{{\it\alpha}{\it\beta}}$
are no longer of any significance. But the sum of
all the
$K_{{\it\alpha}{\it\beta}}$
are no longer of any significance. But the sum of
all the
![]() $K_{{\it\alpha}{\it\beta}}$
is still invariant. This is just the total magnetic helicity
$K_{{\it\alpha}{\it\beta}}$
is still invariant. This is just the total magnetic helicity
 $$\begin{eqnarray}K_{0}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}=\text{invariant}.\end{eqnarray}$$
$$\begin{eqnarray}K_{0}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}=\text{invariant}.\end{eqnarray}$$
(Apart from the fact that they are rendered irrelevant by reconnection, the
individual
![]() $K_{{\it\alpha}{\it\beta}}$
differ from the total helicity
$K_{{\it\alpha}{\it\beta}}$
differ from the total helicity
![]() $K_{0}$
in another fundamental way. For the
$K_{0}$
in another fundamental way. For the
![]() $K_{{\it\alpha}{\it\beta}}$
to be relevant, we would need to calculate and identify all the
field lines – a knowledge of the field
$K_{{\it\alpha}{\it\beta}}$
to be relevant, we would need to calculate and identify all the
field lines – a knowledge of the field
![]() $\boldsymbol{B}$
itself is not enough – whereas
$\boldsymbol{B}$
itself is not enough – whereas
![]() $K_{0}$
is well defined by the field alone. In a loose analogy with
particle dynamics, we could say that
$K_{0}$
is well defined by the field alone. In a loose analogy with
particle dynamics, we could say that
![]() $K_{0}$
is an isolating integral, which constrains the available
configuration space, whereas the
$K_{0}$
is an isolating integral, which constrains the available
configuration space, whereas the
![]() $K_{{\it\alpha}{\it\beta}}$
are non-isolating integrals, which do not constrain the evolution
of the field.)
$K_{{\it\alpha}{\it\beta}}$
are non-isolating integrals, which do not constrain the evolution
of the field.)
We conclude, therefore, that the relaxed state of a slightly resistive turbulent
plasma is obtained by minimising the magnetic energy subject to a single constraint,
here denoted by the Lagrange multiplier
![]() ${\it\mu}$
,
${\it\mu}$
,
 $$\begin{eqnarray}{\it\delta}\int \left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}\,\text{d}{\it\tau}-{\it\mu}\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\,\text{d}{\it\tau}\right]_{all\,{\it\delta}\boldsymbol{A}}=0.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\int \left[\frac{1}{2}(\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})^{2}\,\text{d}{\it\tau}-{\it\mu}\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\,\text{d}{\it\tau}\right]_{all\,{\it\delta}\boldsymbol{A}}=0.\end{eqnarray}$$
That is
 $$\begin{eqnarray}{\it\delta}\boldsymbol{A}\boldsymbol{\cdot }\{\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-2{\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\}=0,\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}\boldsymbol{A}\boldsymbol{\cdot }\{\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})-2{\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}\}=0,\end{eqnarray}$$
and upon redefining
![]() ${\it\mu}$
, finally
${\it\mu}$
, finally
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}.\end{eqnarray}$$
This is no longer any force-free state, depending on
the initial conditions; it is a unique state dependent only on a single parameter
![]() ${\it\mu}$
. Thus we have already recovered the uniqueness of the quiescent
phase.
${\it\mu}$
. Thus we have already recovered the uniqueness of the quiescent
phase.
7.2. Helicity and field line linkage
Before discussing properties of the relaxed states given by (7.21), we should note some features of
the magnetic helicity
![]() $K_{0}$
.
$K_{0}$
.
The helicity
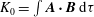 $K_{0}=\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is defined only if the volume of integration is
bounded by a closed flux surface. Otherwise it is not gauge-invariant. This reflects
the fact that
$K_{0}=\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is defined only if the volume of integration is
bounded by a closed flux surface. Otherwise it is not gauge-invariant. This reflects
the fact that
![]() $\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
is not a local quantity. One cannot specify where the helicity
resides, or a helicity density; only the total helicity within a closed flux surface
can be defined.
$\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
is not a local quantity. One cannot specify where the helicity
resides, or a helicity density; only the total helicity within a closed flux surface
can be defined.
In fact, helicity is a topological quantity related to the linkage of one flux tube
with another. For example, for two flux tubes as in figure 17, the helicity is
 $K_{0}=2{\it\psi}_{1}{\it\psi}_{2}$
if they are linked as in the figure, and zero if they are not
linked (Moffat Reference Moffat1978). Where
the helicity is located when they are linked is a meaningless question.
$K_{0}=2{\it\psi}_{1}{\it\psi}_{2}$
if they are linked as in the figure, and zero if they are not
linked (Moffat Reference Moffat1978). Where
the helicity is located when they are linked is a meaningless question.

Figure 17. Linked flux tubes.
If the volume concerned is multiply connected, as in a torus, then even though the
bounding surface is a flux tube, the simple formula (7.18) for
![]() $K_{0}$
is not fully gauge-invariant. The full gauge-invariant form should
be
$K_{0}$
is not fully gauge-invariant. The full gauge-invariant form should
be
 $$\begin{eqnarray}K_{1}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}-\oint _{C_{1}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\oint _{C_{2}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s},\end{eqnarray}$$
$$\begin{eqnarray}K_{1}=\int _{V}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}-\oint _{C_{1}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\oint _{C_{2}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s},\end{eqnarray}$$
where
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are circuits the long and short way around the torus boundary.
However, in most applications the circuit integrals are themselves constant and the
simpler form can be used.
$C_{2}$
are circuits the long and short way around the torus boundary.
However, in most applications the circuit integrals are themselves constant and the
simpler form can be used.
7.3. Back to reality
If all this sounds too much like exotic mathematics, there is a down-to-earth
engineering interpretation of
![]() $K_{0}$
– as the volt-seconds from the driving transformer. (Volt-seconds
are a standard measure of transformer performance and something you would certainly
know was real if you touched the terminals!)
$K_{0}$
– as the volt-seconds from the driving transformer. (Volt-seconds
are a standard measure of transformer performance and something you would certainly
know was real if you touched the terminals!)
To see this connection, we introduce a small gap in the toroidal shell, as in
figure 18, in order to apply the loop
voltage
![]() $V_{loop}$
. Then, using (7.22)
$V_{loop}$
. Then, using (7.22)
 $$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=\int _{S}\left(\boldsymbol{A}\times \frac{\partial \boldsymbol{A}}{\partial t}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}-\oint _{C_{1}}\frac{\partial \boldsymbol{A}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\oint _{C_{2}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=\int _{S}\left(\boldsymbol{A}\times \frac{\partial \boldsymbol{A}}{\partial t}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}-\oint _{C_{1}}\frac{\partial \boldsymbol{A}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\oint _{C_{2}}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}.\end{eqnarray}$$
But
 $\partial \boldsymbol{A}/\partial t\neq 0$
only in the gap. There we may write
$\partial \boldsymbol{A}/\partial t\neq 0$
only in the gap. There we may write
 $\text{d}\boldsymbol{S}=\text{d}\boldsymbol{l}\times \text{d}\boldsymbol{s}$
and
$\text{d}\boldsymbol{S}=\text{d}\boldsymbol{l}\times \text{d}\boldsymbol{s}$
and
 $$\begin{eqnarray}\int _{S}\left(\boldsymbol{A}\times \frac{\partial \boldsymbol{A}}{\partial t}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}\rightarrow -\oint (\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s})\oint \left(\frac{\partial \boldsymbol{A}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\right),\end{eqnarray}$$
$$\begin{eqnarray}\int _{S}\left(\boldsymbol{A}\times \frac{\partial \boldsymbol{A}}{\partial t}\right)\boldsymbol{\cdot }\text{d}\boldsymbol{S}\rightarrow -\oint (\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s})\oint \left(\frac{\partial \boldsymbol{A}}{\partial t}\boldsymbol{\cdot }\text{d}\boldsymbol{l}\right),\end{eqnarray}$$
where
 $\oint (\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s})={\it\Psi}_{tor}$
and
$\oint (\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s})={\it\Psi}_{tor}$
and
 $\oint (\partial _{t}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l})=-V_{loop}$
so
$\oint (\partial _{t}\boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l})=-V_{loop}$
so
 $$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}\rightarrow 2{\it\Psi}_{tor}V_{loop}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}\rightarrow 2{\it\Psi}_{tor}V_{loop}.\end{eqnarray}$$
Therefore, if loop volts are applied at a constant toroidal flux,
 $$\begin{eqnarray}\frac{K}{2{\it\Psi}_{tor}}=\text{volt-seconds stored in plasma}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{K}{2{\it\Psi}_{tor}}=\text{volt-seconds stored in plasma}.\end{eqnarray}$$

Figure 18. Interpreting magnetic helicity in terms of stored volt-seconds.
In principle (7.25) and (7.26) describe the start-up of the toroidal plasma, but as this is ill-controlled and volt-seconds are lost in ionisation and heating, we cannot usefully apply them to this initial stage. (The start-up loop voltage is much larger than that required to maintain the relaxed state.)
7.4. Uniqueness of relaxed states
In the next few lectures we will discuss specific solutions of equation (7.21) for relaxed states. But first we
show that each relaxed state is uniquely determined – with no arbitrary or fitted
parameters – by the externally controlled quantities
![]() ${\it\Psi}_{tor}$
and
${\it\Psi}_{tor}$
and
![]() $K$
. To see this, scale all dimensions in the problem by
$K$
. To see this, scale all dimensions in the problem by
![]() ${\it\mu}$
. It is then clear, if it was not already, that the solution of
(7.21) must be of the form
${\it\mu}$
. It is then clear, if it was not already, that the solution of
(7.21) must be of the form
 $\boldsymbol{B}=c\,\hat{\boldsymbol{B}}({\it\mu}\boldsymbol{r};{\it\mu}a,{\it\mu}R)$
,
$\boldsymbol{B}=c\,\hat{\boldsymbol{B}}({\it\mu}\boldsymbol{r};{\it\mu}a,{\it\mu}R)$
,
 $\boldsymbol{A}=(c/{\it\mu})\hat{\boldsymbol{A}}({\it\mu}\boldsymbol{r};{\it\mu}a,{\it\mu}R)$
, where
$\boldsymbol{A}=(c/{\it\mu})\hat{\boldsymbol{A}}({\it\mu}\boldsymbol{r};{\it\mu}a,{\it\mu}R)$
, where
![]() $a$
and
$a$
and
![]() $R$
are minor and major radii and
$R$
are minor and major radii and
![]() $c$
is the arbitrary scale factor (Taylor Reference Taylor1974b
). Then
$c$
is the arbitrary scale factor (Taylor Reference Taylor1974b
). Then
 $$\begin{eqnarray}K=\int \frac{c^{2}}{{\it\mu}}\hat{B}({\it\rho})\hat{A}({\it\rho})\,\frac{\text{d}^{3}{\it\rho}}{{\it\mu}^{3}}\sim \frac{c^{2}}{{\it\mu}^{4}}F({\it\mu}a,{\it\mu}R)\end{eqnarray}$$
$$\begin{eqnarray}K=\int \frac{c^{2}}{{\it\mu}}\hat{B}({\it\rho})\hat{A}({\it\rho})\,\frac{\text{d}^{3}{\it\rho}}{{\it\mu}^{3}}\sim \frac{c^{2}}{{\it\mu}^{4}}F({\it\mu}a,{\it\mu}R)\end{eqnarray}$$
and
 $$\begin{eqnarray}{\it\Psi}_{tor}=\int c\hat{B}({\it\rho})\,\frac{\text{d}^{2}{\it\rho}}{{\it\mu}^{2}}\sim \frac{c}{{\it\mu}^{2}}G({\it\mu}a,{\it\mu}R),\end{eqnarray}$$
$$\begin{eqnarray}{\it\Psi}_{tor}=\int c\hat{B}({\it\rho})\,\frac{\text{d}^{2}{\it\rho}}{{\it\mu}^{2}}\sim \frac{c}{{\it\mu}^{2}}G({\it\mu}a,{\it\mu}R),\end{eqnarray}$$
giving
 $$\begin{eqnarray}\frac{K}{{\it\Psi}_{tor}^{2}}=\text{function of }({\it\mu}a,{\it\mu}R),\end{eqnarray}$$
$$\begin{eqnarray}\frac{K}{{\it\Psi}_{tor}^{2}}=\text{function of }({\it\mu}a,{\it\mu}R),\end{eqnarray}$$
which fixes
![]() ${\it\mu}$
. The scale factor
${\it\mu}$
. The scale factor
![]() $c$
can then be set from
$c$
can then be set from
![]() $K$
or
$K$
or
![]() ${\it\Psi}_{tor}$
.
${\it\Psi}_{tor}$
.
7.5. Summary
Now let us summarise what we have seen so far. Observations of
turbulent plasmas in a toroidal pinch, with initial toroidal
field
![]() $B_{0}$
and current
$B_{0}$
and current
![]() $I$
, have shown that quiescent states form that depend only on the
parameter
$I$
, have shown that quiescent states form that depend only on the
parameter
 ${\it\theta}\equiv 2I/aB_{0}$
, and if
${\it\theta}\equiv 2I/aB_{0}$
, and if
![]() ${\it\theta}>{\it\theta}_{c}$
the toroidal field spontaneously reverses.
${\it\theta}>{\it\theta}_{c}$
the toroidal field spontaneously reverses.
We interpret these as ‘relaxed’ states, that is, states of minimum energy subject to
constraints. In an ideal plasma there would be an infinity of constraints, but this
leads to a state in strong disagreement with observations. In a slightly resistive
plasma, the infinity of individual constraints become irrelevant and the only
surviving constraint is that the total magnetic helicity
 $K_{{\it\alpha}{\it\beta}}=\int _{{\it\alpha}{\it\beta}}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is invariant. This leads to relaxed states in agreement with
observations, as we shall see in detail in the following sections.
$K_{{\it\alpha}{\it\beta}}=\int _{{\it\alpha}{\it\beta}}\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is invariant. This leads to relaxed states in agreement with
observations, as we shall see in detail in the following sections.
8. Relaxed states in toroidal pinch
Now, at last, we turn to calculating a relaxed state. We first consider a toroidal pinch
surrounded by a conducting shell, represented by the boundary condition
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
(see figure 4). As we know, such
a system has two invariants,
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
(see figure 4). As we know, such
a system has two invariants,
![]() $K$
and
$K$
and
![]() ${\it\psi}_{tor}$
, and these completely specify the relaxed state.
${\it\psi}_{tor}$
, and these completely specify the relaxed state.
For simplicity, we first solve
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}$
for the relaxed state in a cylinder, which can be considered an
approximation for a large-aspect-ratio toroidal pinch. The magnetic field then depends
only on the minor radius, so that
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}$
for the relaxed state in a cylinder, which can be considered an
approximation for a large-aspect-ratio toroidal pinch. The magnetic field then depends
only on the minor radius, so that
![]() $B_{r}=0$
,
$B_{r}=0$
,
 $B_{{\it\theta}}=B_{{\it\theta}}(r)$
,
$B_{{\it\theta}}=B_{{\it\theta}}(r)$
,
 $B_{z}=B_{z}(r)$
and
$B_{z}=B_{z}(r)$
and
 $$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\partial B_{z}}{\partial r}={\it\mu}B_{{\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\partial B_{z}}{\partial r}={\it\mu}B_{{\it\theta}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial r}(rB_{{\it\theta}})={\it\mu}B_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial r}(rB_{{\it\theta}})={\it\mu}B_{z}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial B_{z}}{\partial r}\right)+{\it\mu}^{2}B_{z}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial B_{z}}{\partial r}\right)+{\it\mu}^{2}B_{z}=0.\end{eqnarray}$$
Therefore
 $$\begin{eqnarray}B_{z}={\it\alpha}\text{J}_{0}({\it\mu}r),\quad B_{{\it\theta}}={\it\alpha}\text{J}_{1}({\it\mu}r).\end{eqnarray}$$
$$\begin{eqnarray}B_{z}={\it\alpha}\text{J}_{0}({\it\mu}r),\quad B_{{\it\theta}}={\it\alpha}\text{J}_{1}({\it\mu}r).\end{eqnarray}$$
Unsurprisingly, this is known as the Bessel function profile.
Integration of (8.2) shows that the
pinch ratio
 ${\it\theta}={\it\mu}a/2$
. A further calculation relates the parameter
${\it\theta}={\it\mu}a/2$
. A further calculation relates the parameter
![]() ${\it\mu}$
to
${\it\mu}$
to
![]() $K/{\it\Psi}_{tor}^{2}$
as in (7.29),
$K/{\it\Psi}_{tor}^{2}$
as in (7.29),
 $$\begin{eqnarray}\frac{K}{{\it\Psi}^{2}}=\frac{l}{2{\rm\pi}a}\left\{\frac{{\it\mu}a[\text{J}_{0}^{2}({\it\mu}a)+\text{J}_{1}^{2}({\it\mu}a)]-2\text{J}_{0}({\it\mu}a)\text{J}_{1}({\it\mu}a)}{\text{J}_{1}^{2}({\it\mu}a)}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\frac{K}{{\it\Psi}^{2}}=\frac{l}{2{\rm\pi}a}\left\{\frac{{\it\mu}a[\text{J}_{0}^{2}({\it\mu}a)+\text{J}_{1}^{2}({\it\mu}a)]-2\text{J}_{0}({\it\mu}a)\text{J}_{1}({\it\mu}a)}{\text{J}_{1}^{2}({\it\mu}a)}\right\},\end{eqnarray}$$
where
![]() $l$
is the cylinder length, identified with
$l$
is the cylinder length, identified with
![]() $2{\rm\pi}R$
in a torus.
$2{\rm\pi}R$
in a torus.
The Bessel profile fits the experimental data remarkably well, as can be seen in figure 19 and in Bodin (Reference Bodin1983, Reference Bodin, Tran and Verbeek1984, Reference Bodin, Ortolani and Sindoni1987).

Figure 19. Comparison of experimental magnetic field profiles in the quiescent state of the toroidal pinch HBTX-1A to the theoretical expressions (8.4). (Reproduced with permission from Bodin (Reference Bodin, Tran and Verbeek1984).)
8.1. Spontaneous field reversal
Since the ‘toroidal’ field is
 $B_{z}\sim \text{J}_{0}({\it\mu}r)$
, it is clear that the onset of spontaneous field reversal in the
relaxed state occurs at
$B_{z}\sim \text{J}_{0}({\it\mu}r)$
, it is clear that the onset of spontaneous field reversal in the
relaxed state occurs at
 ${\it\mu}a>2.4$
. This corresponds to an experimental pinch parameter
${\it\mu}a>2.4$
. This corresponds to an experimental pinch parameter
![]() ${\it\theta}>1.2$
– which again agrees well with the experimental observations.
${\it\theta}>1.2$
– which again agrees well with the experimental observations.
The experimental data from reverse field pinches (RFPs) is usually presented in the
form of an
![]() $F{-}{\it\theta}$
diagram, where
$F{-}{\it\theta}$
diagram, where
 $$\begin{eqnarray}F\equiv \frac{B_{toroidal}^{(wall)}}{\langle B_{toroidal}\rangle },\end{eqnarray}$$
$$\begin{eqnarray}F\equiv \frac{B_{toroidal}^{(wall)}}{\langle B_{toroidal}\rangle },\end{eqnarray}$$
and the angled brackets denote the average over the cross-section.
The value of
![]() $F$
in the relaxed state is
$F$
in the relaxed state is
 $$\begin{eqnarray}F=\frac{2{\it\theta}\text{J}_{0}(2{\it\theta})}{\text{J}_{1}(2{\it\theta})}.\end{eqnarray}$$
$$\begin{eqnarray}F=\frac{2{\it\theta}\text{J}_{0}(2{\it\theta})}{\text{J}_{1}(2{\it\theta})}.\end{eqnarray}$$
Note that this is calculated from ‘first principles’, and contains no empirical or fitted factors.
Equation (8.7) is in good agreement
with experiment, as can be seen in figure 20.
Note that the experimental points from several machines lie on a universal curve,
close to the theoretical one but at somewhat higher
![]() ${\it\theta}$
. (This may be due to the lower current density near the wall, where
the plasma is contaminated by impurities.)
${\it\theta}$
. (This may be due to the lower current density near the wall, where
the plasma is contaminated by impurities.)

Figure 20. An
![]() $F{-}{\it\theta}$
diagram showing data from the pinch experiments HBTX1,
ALPHA and ZETA and the theoretical curve. (Reproduced with permission from
Bodin & Newton (Reference Bodin and Newton1980).)
$F{-}{\it\theta}$
diagram showing data from the pinch experiments HBTX1,
ALPHA and ZETA and the theoretical curve. (Reproduced with permission from
Bodin & Newton (Reference Bodin and Newton1980).)
Even more striking evidence for relaxation can be seen in the time-dependent
behaviour shown in figure 21. We see that if
the operating point
![]() $(F,{\it\theta})$
is forced away from the locus of relaxed states (e.g. by a
temporary increase in loop voltage), it very quickly (
$(F,{\it\theta})$
is forced away from the locus of relaxed states (e.g. by a
temporary increase in loop voltage), it very quickly (
![]() $0.8~{\rm\mu}\text{s}$
! – comparable to the Alfvén time
$0.8~{\rm\mu}\text{s}$
! – comparable to the Alfvén time
![]() ${\sim}1~{\rm\mu}\text{s}$
) reverts back to it. However, as long as the operating point is
changed slowly, the plasma stays close to the theoretical relaxed-state curve
(figures 21
b and 22).
${\sim}1~{\rm\mu}\text{s}$
) reverts back to it. However, as long as the operating point is
changed slowly, the plasma stays close to the theoretical relaxed-state curve
(figures 21
b and 22).

Figure 21. Time-dependent
![]() $F{-}{\it\theta}$
curve for HBTX1 in (a) fast mode and
(b) slow mode. Time intervals are given in microseconds.
(Reproduced with permission from Bodin & Newton (Reference Bodin and Newton1980).)
$F{-}{\it\theta}$
curve for HBTX1 in (a) fast mode and
(b) slow mode. Time intervals are given in microseconds.
(Reproduced with permission from Bodin & Newton (Reference Bodin and Newton1980).)

Figure 22. Time-dependent
![]() $F{-}{\it\theta}$
curves from pinches operated in slow mode:
(a) ZT-40 experiment (from DiMarco Reference DiMarco, Post, Baldwin and Ryutov1983), (b) TPRE experiment (reproduced
with permission from Tamaru et al.
Reference Tamaru, Sugisaki, Hayase, Shimada, Hirano, Maejima, Ogawa, Hirano, Kitagawa and Sato1979) and (c) REPUTE
experiment (reproduced with permission from Toyama et al.
Reference Toyama, Asakura, Hattori, Inoue, Ishida, Matsuzuka, Miyamoto, Morikawa, Nagayama, Nihei, Shinohara, Ueda, Yamagishi, Yoshida, Pocs and Montvai1985).
$F{-}{\it\theta}$
curves from pinches operated in slow mode:
(a) ZT-40 experiment (from DiMarco Reference DiMarco, Post, Baldwin and Ryutov1983), (b) TPRE experiment (reproduced
with permission from Tamaru et al.
Reference Tamaru, Sugisaki, Hayase, Shimada, Hirano, Maejima, Ogawa, Hirano, Kitagawa and Sato1979) and (c) REPUTE
experiment (reproduced with permission from Toyama et al.
Reference Toyama, Asakura, Hattori, Inoue, Ishida, Matsuzuka, Miyamoto, Morikawa, Nagayama, Nihei, Shinohara, Ueda, Yamagishi, Yoshida, Pocs and Montvai1985).
9. Energetics of toroidal relaxed states
Actually, determination of the relaxed state is more complex than the analysis so far
suggests. This is because there may be more than one solution of (7.21) compatible with
![]() $K$
,
$K$
,
![]() ${\it\Psi}$
and the boundary conditions. Therefore, in any situation we must
consider all possible solutions of (7.21) and select that which has the lowest energy.
${\it\Psi}$
and the boundary conditions. Therefore, in any situation we must
consider all possible solutions of (7.21) and select that which has the lowest energy.
In a cylinder we can find all the solutions of (7.21) explicitly (Taylor Reference Taylor1968). Any solution, whether axisymmetric or not, satisfies
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial {\it\theta}}B_{z}-\frac{\partial }{\partial z}B_{{\it\phi}}={\it\mu}B_{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial {\it\theta}}B_{z}-\frac{\partial }{\partial z}B_{{\it\phi}}={\it\mu}B_{r}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial B_{r}}{\partial z}-\frac{\partial B_{z}}{\partial r}={\it\mu}B_{{\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial B_{r}}{\partial z}-\frac{\partial B_{z}}{\partial r}={\it\mu}B_{{\it\theta}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial r}(rB_{{\it\theta}})-\frac{1}{r}\frac{\partial B_{r}}{\partial {\it\theta}}={\it\mu}B_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{r}\frac{\partial }{\partial r}(rB_{{\it\theta}})-\frac{1}{r}\frac{\partial B_{r}}{\partial {\it\theta}}={\it\mu}B_{z}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{B})={\it\mu}^{2}\boldsymbol{B}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{B})={\it\mu}^{2}\boldsymbol{B}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}{\rm\nabla}^{2}B_{z}+{\it\mu}^{2}B_{z}=0,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\nabla}^{2}B_{z}+{\it\mu}^{2}B_{z}=0,\end{eqnarray}$$
and then compute the other components of
![]() $\boldsymbol{B}$
from (9.4).
$\boldsymbol{B}$
from (9.4).
The general solution of (9.5) can be
expressed as a sum of Fourier modes
 $B_{z}=h(r)\cos (m{\it\theta}+kz)$
, where
$B_{z}=h(r)\cos (m{\it\theta}+kz)$
, where
 $$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial h}{\partial r}\right)-\left(\frac{m^{2}}{r^{2}}+k^{2}\right)h+{\it\mu}^{2}h=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial h}{\partial r}\right)-\left(\frac{m^{2}}{r^{2}}+k^{2}\right)h+{\it\mu}^{2}h=0,\end{eqnarray}$$
so that
 $$\begin{eqnarray}h(r)=\text{J}_{m}(y),\quad \text{where }y\equiv r({\it\mu}^{2}-k^{2})^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}h(r)=\text{J}_{m}(y),\quad \text{where }y\equiv r({\it\mu}^{2}-k^{2})^{1/2}.\end{eqnarray}$$
The general form of the relaxed state in a cylinder therefore becomes
 $$\begin{eqnarray}\boldsymbol{B}=\mathop{\sum }_{m,k}a_{mk}\boldsymbol{B}^{mk}(\boldsymbol{r}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\mathop{\sum }_{m,k}a_{mk}\boldsymbol{B}^{mk}(\boldsymbol{r}),\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{r}^{mk}=-\frac{1}{({\it\mu}^{2}-k^{2})^{1/2}}\left\{k\text{J}_{m}^{\prime }(y)+\frac{m{\it\mu}}{y}\text{J}_{m}(y)\right\}\sin (m{\it\theta}+kz), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{r}^{mk}=-\frac{1}{({\it\mu}^{2}-k^{2})^{1/2}}\left\{k\text{J}_{m}^{\prime }(y)+\frac{m{\it\mu}}{y}\text{J}_{m}(y)\right\}\sin (m{\it\theta}+kz), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}^{mk}=-\frac{1}{({\it\mu}^{2}-k^{2})^{1/2}}\left\{{\it\mu}\text{J}_{m}^{\prime }(y)+\frac{mk}{y}\text{J}_{m}(y)\right\}\cos (m{\it\theta}+kz), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}^{mk}=-\frac{1}{({\it\mu}^{2}-k^{2})^{1/2}}\left\{{\it\mu}\text{J}_{m}^{\prime }(y)+\frac{mk}{y}\text{J}_{m}(y)\right\}\cos (m{\it\theta}+kz), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{z}^{mk}=\text{J}_{m}(y)\cos (m{\it\theta}+kz). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{z}^{mk}=\text{J}_{m}(y)\cos (m{\it\theta}+kz). & \displaystyle\end{eqnarray}$$
In the general solution (9.8), the
 $(m=0,k=0)$
term is of a different character to all the others. It satisfies the
boundary condition
$(m=0,k=0)$
term is of a different character to all the others. It satisfies the
boundary condition
![]() $B_{r}=0$
for any value of
$B_{r}=0$
for any value of
![]() ${\it\mu}$
and it carries non-zero toroidal flux. All other terms satisfy the
boundary condition only for discrete values of
${\it\mu}$
and it carries non-zero toroidal flux. All other terms satisfy the
boundary condition only for discrete values of
 ${\it\mu}~(={\it\mu}_{mk})$
given by
${\it\mu}~(={\it\mu}_{mk})$
given by
 $$\begin{eqnarray}k\text{J}_{m}^{\prime }[({\it\mu}^{2}-k^{2})^{1/2}a]+\frac{m{\it\mu}}{({\it\mu}^{2}-k^{2})^{1/2}a}\text{J}_{m}[({\it\mu}^{2}-k^{2})^{1/2}a]=0,\end{eqnarray}$$
$$\begin{eqnarray}k\text{J}_{m}^{\prime }[({\it\mu}^{2}-k^{2})^{1/2}a]+\frac{m{\it\mu}}{({\it\mu}^{2}-k^{2})^{1/2}a}\text{J}_{m}[({\it\mu}^{2}-k^{2})^{1/2}a]=0,\end{eqnarray}$$
and they carry no toroidal flux. Consequently, there are two distinct types of relaxed state in a cylinder.
Type I: the primitive or symmetric state, consisting solely of the
 $(m=0,k=0)$
term. This is the Bessel state we have already discussed, in which
$(m=0,k=0)$
term. This is the Bessel state we have already discussed, in which
![]() ${\it\mu}$
is determined by
${\it\mu}$
is determined by
![]() $K/{\it\Psi}^{2}$
.
$K/{\it\Psi}^{2}$
.
Type II: a mixed or helical state made up of an
 $(m=0,k=0)$
term, to provide the required toroidal flux, plus one
term with
$(m=0,k=0)$
term, to provide the required toroidal flux, plus one
term with
![]() $m$
and
$m$
and
![]() $k$
non-zero, i.e.
$k$
non-zero, i.e.
 $\boldsymbol{B}={\it\alpha}_{0}\boldsymbol{B}^{00}+{\it\alpha}_{mk}\boldsymbol{B}^{mk}$
(no summation over
$\boldsymbol{B}={\it\alpha}_{0}\boldsymbol{B}^{00}+{\it\alpha}_{mk}\boldsymbol{B}^{mk}$
(no summation over
![]() $m$
,
$m$
,
![]() $k$
). In this mixed state
$k$
). In this mixed state
![]() ${\it\mu}(m,k)$
is given by (9.12).
Consequently,
${\it\mu}(m,k)$
is given by (9.12).
Consequently,
![]() ${\it\mu}$
is no longer determined by
${\it\mu}$
is no longer determined by
![]() $K/{\it\Psi}^{2}$
; instead, with
$K/{\it\Psi}^{2}$
; instead, with
![]() ${\it\mu}$
fixed,
${\it\mu}$
fixed,
![]() $K/{\it\Psi}^{2}$
determines the mixing ratio
$K/{\it\Psi}^{2}$
determines the mixing ratio
![]() ${\it\alpha}_{mk}/{\it\alpha}_{0}$
.
${\it\alpha}_{mk}/{\it\alpha}_{0}$
.
Both Type I and Type II relaxed states are therefore fully determined by
![]() $K$
and
$K$
and
![]() ${\it\Psi}$
, but in quite different ways. We now need to find which relaxed state
has the lowest energy, and, if it is a Type II, what are the specific values of
${\it\Psi}$
, but in quite different ways. We now need to find which relaxed state
has the lowest energy, and, if it is a Type II, what are the specific values of
![]() $m$
and
$m$
and
![]() $k$
.
$k$
.
9.1. Primitive and mixed states
The task of finding which is the lowest-energy solution is made easier by two comparison theorems (Taylor Reference Taylor1968):
(i) The first theorem is that if two solutions have the same value of
![]() ${\it\Psi}$
and
${\it\Psi}$
and
![]() $K$
, then the one with the smaller
$K$
, then the one with the smaller
![]() ${\it\mu}$
has the lower energy. The proof of this is as follows.
${\it\mu}$
has the lower energy. The proof of this is as follows.
If
 $\int \boldsymbol{A}_{1}\boldsymbol{\cdot }\boldsymbol{B}_{1}\;\text{d}{\it\tau}=\int \boldsymbol{A}_{2}\boldsymbol{\cdot }\boldsymbol{B}_{2}\;\text{d}{\it\tau}$
with
$\int \boldsymbol{A}_{1}\boldsymbol{\cdot }\boldsymbol{B}_{1}\;\text{d}{\it\tau}=\int \boldsymbol{A}_{2}\boldsymbol{\cdot }\boldsymbol{B}_{2}\;\text{d}{\it\tau}$
with
![]() $\boldsymbol{A}_{1}=\boldsymbol{A}_{2}$
on the boundary, and both
$\boldsymbol{A}_{1}=\boldsymbol{A}_{2}$
on the boundary, and both
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{1}={\it\mu}_{1}\boldsymbol{B}_{1}$
and
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{1}={\it\mu}_{1}\boldsymbol{B}_{1}$
and
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{2}={\it\mu}_{2}\boldsymbol{B}_{2}$
, then
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{2}={\it\mu}_{2}\boldsymbol{B}_{2}$
, then
 $$\begin{eqnarray}\int [\boldsymbol{{\rm\nabla}}\times (\boldsymbol{A}_{1}-\boldsymbol{A}_{2})]^{2}\;\text{d}{\it\tau}=({\it\mu}_{2}+{\it\mu}_{1})\int (\boldsymbol{A}_{2}-\boldsymbol{A}_{1})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2}\;\text{d}{\it\tau}\end{eqnarray}$$
$$\begin{eqnarray}\int [\boldsymbol{{\rm\nabla}}\times (\boldsymbol{A}_{1}-\boldsymbol{A}_{2})]^{2}\;\text{d}{\it\tau}=({\it\mu}_{2}+{\it\mu}_{1})\int (\boldsymbol{A}_{2}-\boldsymbol{A}_{1})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2}\;\text{d}{\it\tau}\end{eqnarray}$$
and
 $$\begin{eqnarray}\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2})^{2}\;\text{d}{\it\tau}-\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{1})^{2}\;\text{d}{\it\tau}=({\it\mu}_{2}-{\it\mu}_{1})\int (\boldsymbol{A}_{2}-\boldsymbol{A}_{1})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2}\;\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2})^{2}\;\text{d}{\it\tau}-\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{1})^{2}\;\text{d}{\it\tau}=({\it\mu}_{2}-{\it\mu}_{1})\int (\boldsymbol{A}_{2}-\boldsymbol{A}_{1})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{2}\;\text{d}{\it\tau}.\end{eqnarray}$$
Therefore, if
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
are the energies of two relaxed states, then
$W_{2}$
are the energies of two relaxed states, then
 $$\begin{eqnarray}W_{2}-W_{1}=\frac{{\it\mu}_{2}^{2}-{\it\mu}_{1}^{2}}{({\it\mu}_{2}+{\it\mu}_{1})^{2}}\int \frac{(B_{2}-B_{1})^{2}}{2}\;\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}W_{2}-W_{1}=\frac{{\it\mu}_{2}^{2}-{\it\mu}_{1}^{2}}{({\it\mu}_{2}+{\it\mu}_{1})^{2}}\int \frac{(B_{2}-B_{1})^{2}}{2}\;\text{d}{\it\tau}.\end{eqnarray}$$
Hence, if
![]() ${\it\mu}_{2}^{2}>{\it\mu}_{1}^{2}$
,
${\it\mu}_{2}^{2}>{\it\mu}_{1}^{2}$
,
 $W_{2}>W_{1}$
.
$W_{2}>W_{1}$
.
(ii) The second theorem is that the eigenvalues of (9.12) for the same
![]() $k$
increase with increasing
$k$
increase with increasing
![]() $m$
. The proof of this is similar to the argument above and to the
Sturm–Liouville comparison theorems in the theory of differential equations (Ince
Reference Ince1956).
$m$
. The proof of this is similar to the argument above and to the
Sturm–Liouville comparison theorems in the theory of differential equations (Ince
Reference Ince1956).
By theorem (i), to find the solution with the lowest energy, we must select that with
the smallest
![]() ${\it\mu}$
. For a Type I solution this means taking the smallest root of
(8.5). By theorem (ii), for a
Type II solution it means taking
${\it\mu}$
. For a Type I solution this means taking the smallest root of
(8.5). By theorem (ii), for a
Type II solution it means taking
![]() $m=1$
and then searching through
$m=1$
and then searching through
![]() $k$
at
$k$
at
![]() $m=1$
to find the smallest eigenvalue of (9.12). This occurs at
$m=1$
to find the smallest eigenvalue of (9.12). This occurs at
 $ka\approx 1.25$
and has the value
$ka\approx 1.25$
and has the value
 ${\it\mu}a=3.11$
.
${\it\mu}a=3.11$
.
This essentially completes the solution of our problem. The primitive solution
 $\boldsymbol{B}={\it\alpha}\boldsymbol{B}^{00}$
is the correct relaxed state so long as
$\boldsymbol{B}={\it\alpha}\boldsymbol{B}^{00}$
is the correct relaxed state so long as
 ${\it\mu}a<3.11$
, i.e.
${\it\mu}a<3.11$
, i.e.
![]() ${\it\theta}\leqslant 1.6$
. Otherwise, the correct state is a mixed, helical state,
${\it\theta}\leqslant 1.6$
. Otherwise, the correct state is a mixed, helical state,
 $\boldsymbol{B}={\it\alpha}_{0}\boldsymbol{B}^{00}+{\it\alpha}_{mk}\boldsymbol{B}^{mk}$
, with
$\boldsymbol{B}={\it\alpha}_{0}\boldsymbol{B}^{00}+{\it\alpha}_{mk}\boldsymbol{B}^{mk}$
, with
![]() $m=1$
,
$m=1$
,
 $k=1.25$
and
$k=1.25$
and
 ${\it\mu}a=3.11$
.
${\it\mu}a=3.11$
.
Recalling that in the primitive state
 ${\it\mu}a=F(K/{\it\Psi}^{2})$
, this is equivalent to saying that the primitive state is the
correct lowest-energy state for
${\it\mu}a=F(K/{\it\Psi}^{2})$
, this is equivalent to saying that the primitive state is the
correct lowest-energy state for
![]() $K/{\it\Psi}^{2}$
less than some critical value, and the mixed state is the correct
one for
$K/{\it\Psi}^{2}$
less than some critical value, and the mixed state is the correct
one for
![]() $K/{\it\Psi}^{2}$
greater than this value. This situation is illustrated
schematically in figure 23. Equally, of course,
we could say that the primitive state occurs when the volt-seconds are below a
critical value and the mixed state occurs when the volt-seconds exceed that
value.
$K/{\it\Psi}^{2}$
greater than this value. This situation is illustrated
schematically in figure 23. Equally, of course,
we could say that the primitive state occurs when the volt-seconds are below a
critical value and the mixed state occurs when the volt-seconds exceed that
value.

Figure 23. Illustration of the energy of the relaxed states in a cylindrical plasma as
a function of
![]() $K/{\it\Psi}^{2}$
.
$K/{\it\Psi}^{2}$
.
9.2. Current saturation and spontaneous symmetry breaking
The Type II helical states with
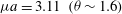 ${\it\mu}a=3.11~({\it\theta}\sim 1.6)$
have a remarkable property. In these states, since
${\it\mu}a=3.11~({\it\theta}\sim 1.6)$
have a remarkable property. In these states, since
![]() ${\it\mu}$
is fixed, an increase in volt-seconds (at fixed
${\it\mu}$
is fixed, an increase in volt-seconds (at fixed
![]() ${\it\Psi}$
) produces no increase in the toroidal current
${\it\Psi}$
) produces no increase in the toroidal current
![]() $I$
! In other words, a helical relaxed state acts as a
current-limiting circuit element! When the voltage is increased,
instead of producing an increase in current, the current remains the same but flows
in a tighter helix with higher inductance. (This is reminiscent of the flexible wire
with which we began the discussion of relaxed states!)
$I$
! In other words, a helical relaxed state acts as a
current-limiting circuit element! When the voltage is increased,
instead of producing an increase in current, the current remains the same but flows
in a tighter helix with higher inductance. (This is reminiscent of the flexible wire
with which we began the discussion of relaxed states!)
Evidence for this second type of relaxed state, and for current saturation, is shown
in figure 24. This shows discharges in which
![]() ${\it\theta}$
is initially driven to a large value. However, it then falls
quickly to
${\it\theta}$
is initially driven to a large value. However, it then falls
quickly to
![]() ${\sim}1.6$
and remains there for the rest of the discharge. (Some discharges
can be prevented from relaxing and held at
${\sim}1.6$
and remains there for the rest of the discharge. (Some discharges
can be prevented from relaxing and held at
![]() ${\it\theta}>1.6$
, but at the cost of increased fluctuation levels and power losses;
see figure 25.)
${\it\theta}>1.6$
, but at the cost of increased fluctuation levels and power losses;
see figure 25.)

Figure 24. Evidence for second critical
![]() ${\it\theta}$
in HBTX1. (Reproduced with permission from Bodin &
Newton (Reference Bodin and Newton1980).)
${\it\theta}$
in HBTX1. (Reproduced with permission from Bodin &
Newton (Reference Bodin and Newton1980).)

Figure 25. Driving a toroidal pinch current above the critical value. Fluctuation level
versus
![]() ${\it\theta}$
in ZT-40. (Reproduced with permission from Watt &
Nebel (Reference Watt and Nebel1983). Copyright 1983, AIP
Publishing LLC.)
${\it\theta}$
in ZT-40. (Reproduced with permission from Watt &
Nebel (Reference Watt and Nebel1983). Copyright 1983, AIP
Publishing LLC.)
The transition from a primitive axisymmetric state to a helical state means that
relaxation theory predicts not one, but two critical values of the pinch parameter
![]() ${\it\theta}$
:
${\it\theta}$
:
-
(i) at
 ${\it\theta}\approx 1.2\rightarrow$
spontaneous field reversal occurs, but the plasma remains
axisymmetric (see § 8.1);
${\it\theta}\approx 1.2\rightarrow$
spontaneous field reversal occurs, but the plasma remains
axisymmetric (see § 8.1); -
(ii) at
 ${\it\theta}\approx 1.6\rightarrow$
current saturation occurs and a helical deformation sets
in (see § 9.1).
${\it\theta}\approx 1.6\rightarrow$
current saturation occurs and a helical deformation sets
in (see § 9.1).
Note that the second transition, from an axisymmetric state to the helical mixed state, is a neat example of ‘spontaneous symmetry breaking’.
9.3. Stability
Like all relaxed states, the relaxed states of the toroidal pinch are ‘minimum energy’ and therefore stable against any perturbations that do not change the helicity. This, of course, includes all ideal MHD perturbations.
The transition from Type I to Type II (helical) relaxed states at
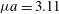 ${\it\mu}a=3.11$
coincides with a linear stability boundary for resistive tearing
modes. However, the present analysis is not restricted to the linear regime. The
nonlinear amplitude of the helical deformation is given precisely in terms of
${\it\mu}a=3.11$
coincides with a linear stability boundary for resistive tearing
modes. However, the present analysis is not restricted to the linear regime. The
nonlinear amplitude of the helical deformation is given precisely in terms of
![]() $K/{\it\Psi}^{2}$
as (Martin & Taylor Reference Martin and Taylor1974; Taylor Reference Taylor1986)
$K/{\it\Psi}^{2}$
as (Martin & Taylor Reference Martin and Taylor1974; Taylor Reference Taylor1986)
 $$\begin{eqnarray}\left(\frac{{\it\alpha}_{1}}{{\it\alpha}_{0}}\right)=0.47\left(\frac{2{\rm\pi}a}{l}\frac{K}{{\it\Psi}^{2}}-8.21\right)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{{\it\alpha}_{1}}{{\it\alpha}_{0}}\right)=0.47\left(\frac{2{\rm\pi}a}{l}\frac{K}{{\it\Psi}^{2}}-8.21\right)^{1/2}.\end{eqnarray}$$
10. The multipinch
The ‘multipinch’, an experiment carried out at General Atomics (La Haye
et al.
Reference La Haye, Jensen, Lee and Ohkawa1986), is important because it shows that
relaxation occurs in experiments other than the RFP, and because its relaxed states show
some striking and unexpected features. The cross-section of the multipinch resembles a
figure eight with height (50 cm) and width (20 cm) chosen to resemble two circular
toroidal pinches one above the other, connected at the ‘waist’ of the figure eight (see
figure 26). The major radius of the torus is
 ${\sim}52~\text{cm}$
and the start-up operation is similar to that of orthodox RFPs.
${\sim}52~\text{cm}$
and the start-up operation is similar to that of orthodox RFPs.

Figure 26. Multipinch experiment at General Atomics. (Reproduced with permission from La Haye et al. (Reference La Haye, Jensen, Lee and Ohkawa1986).)
It is not difficult to calculate the axisymmetric relaxed states of the multipinch (La
Haye et al.
Reference La Haye, Jensen, Lee and Ohkawa1986; Taylor Reference Taylor1986). (Note that we are now discussing a finite-aspect-ratio torus with
non-circular cross-section, not an infinite cylinder.) Using cylindrical coordinates
 $(R,{\it\phi},z)$
, the magnetic field can be written as
$(R,{\it\phi},z)$
, the magnetic field can be written as
 $$\begin{eqnarray}\boldsymbol{B}=\frac{\hat{e}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}{\it\chi}}{R}+\hat{e}_{{\it\phi}}\frac{f}{R}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\frac{\hat{e}_{{\it\phi}}\times \boldsymbol{{\rm\nabla}}{\it\chi}}{R}+\hat{e}_{{\it\phi}}\frac{f}{R}.\end{eqnarray}$$
Then, in the relaxed state
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}$
, we have
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}={\it\mu}\boldsymbol{B}$
, we have
 $\boldsymbol{{\rm\nabla}}f=-{\it\mu}\boldsymbol{{\rm\nabla}}{\it\chi}$
, so that
$\boldsymbol{{\rm\nabla}}f=-{\it\mu}\boldsymbol{{\rm\nabla}}{\it\chi}$
, so that
 $f=C-{\it\mu}{\it\chi}$
, and
$f=C-{\it\mu}{\it\chi}$
, and
 $$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}\equiv \frac{\partial ^{2}{\it\chi}}{\partial z^{2}}+R\frac{\partial }{\partial R}\left(\frac{1}{R}\frac{\partial {\it\chi}}{\partial R}\right)={\it\mu}f.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}\equiv \frac{\partial ^{2}{\it\chi}}{\partial z^{2}}+R\frac{\partial }{\partial R}\left(\frac{1}{R}\frac{\partial {\it\chi}}{\partial R}\right)={\it\mu}f.\end{eqnarray}$$
The boundary condition is
 ${\it\chi}=\text{constant}$
, which without loss of generality can be set to zero. The constant
${\it\chi}=\text{constant}$
, which without loss of generality can be set to zero. The constant
![]() $C$
is fixed by the toroidal flux
$C$
is fixed by the toroidal flux
![]() ${\it\Psi}$
,
${\it\Psi}$
,
 $$\begin{eqnarray}C={\it\mu}\langle {\it\chi}\rangle +\langle R\rangle {\it\Psi}/A,\end{eqnarray}$$
$$\begin{eqnarray}C={\it\mu}\langle {\it\chi}\rangle +\langle R\rangle {\it\Psi}/A,\end{eqnarray}$$
where
![]() $A$
is the cross-sectional area and the averages are defined as
$A$
is the cross-sectional area and the averages are defined as
 $$\begin{eqnarray}\langle \,f\rangle \equiv \left(\int \frac{f}{R}\,\text{d}R\,\text{d}z\right)\left(\int \frac{1}{R}\,\text{d}R\,\text{d}z\right)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \,f\rangle \equiv \left(\int \frac{f}{R}\,\text{d}R\,\text{d}z\right)\left(\int \frac{1}{R}\,\text{d}R\,\text{d}z\right)^{-1}.\end{eqnarray}$$
Then axisymmetric relaxed states are given by
 $$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}({\it\chi}-\langle {\it\chi}\rangle )={\it\mu}\langle R\rangle {\it\Psi}/A.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}({\it\chi}-\langle {\it\chi}\rangle )={\it\mu}\langle R\rangle {\it\Psi}/A.\end{eqnarray}$$
After our experience with the RFP we can anticipate that the eigenfunctions corresponding to (10.5),
 $$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}({\it\chi}-\langle {\it\chi}\rangle )=0,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}({\it\chi}-\langle {\it\chi}\rangle )=0,\end{eqnarray}$$
will also be needed to interpret the behaviour of the multipinch.
Equations (10.5) and (10.6) are Grad–Shafranov-like equations,
albeit unorthodox in that they are non-local through
![]() $\langle {\it\chi}\rangle$
. A solution of (10.5) for a relaxed state is shown in figure 27(a). In addition to being axisymmetric, it is also
symmetric about the equatorial mid-plane, with
$\langle {\it\chi}\rangle$
. A solution of (10.5) for a relaxed state is shown in figure 27(a). In addition to being axisymmetric, it is also
symmetric about the equatorial mid-plane, with
![]() $B_{{\it\phi}}$
the same sign in the upper and lower lobes. The
lowest axisymmetric eigenfunction, calculated from (10.6), has eigenvalue
$B_{{\it\phi}}$
the same sign in the upper and lower lobes. The
lowest axisymmetric eigenfunction, calculated from (10.6), has eigenvalue
 ${\it\mu}a=2.21$
, and is shown in figure 27(b). Note that this is antisymmetric
about the equatorial plane, with
${\it\mu}a=2.21$
, and is shown in figure 27(b). Note that this is antisymmetric
about the equatorial plane, with
![]() $B_{{\it\phi}}$
having opposite sign in the upper and lower lobes. It therefore
carries no net toroidal flux.
$B_{{\it\phi}}$
having opposite sign in the upper and lower lobes. It therefore
carries no net toroidal flux.

Figure 27. Relaxed profiles in the multipinch: (a) primitive relaxed
state, with
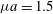 ${\it\mu}a=1.5$
and (b) lowest eigenfunction, with
${\it\mu}a=1.5$
and (b) lowest eigenfunction, with
 ${\it\mu}a=2.21$
. (Reproduced with permission from La Haye
et al. (Reference La Haye, Jensen, Lee and Ohkawa1986).)
${\it\mu}a=2.21$
. (Reproduced with permission from La Haye
et al. (Reference La Haye, Jensen, Lee and Ohkawa1986).)
The toroidal field
![]() $f$
in the relaxed state is given by
$f$
in the relaxed state is given by
 $$\begin{eqnarray}{\rm\Delta}^{+}f+{\it\mu}^{2}f=0,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}^{+}f+{\it\mu}^{2}f=0,\end{eqnarray}$$
with
![]() $f$
constant on the boundary. The value of this constant is again fixed by
the toroidal flux
$f$
constant on the boundary. The value of this constant is again fixed by
the toroidal flux
 $$\begin{eqnarray}\langle \,f\rangle =\frac{\langle R\rangle }{A}{\it\Psi}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \,f\rangle =\frac{\langle R\rangle }{A}{\it\Psi}.\end{eqnarray}$$
The lowest axisymmetric eigenvalue can also be calculated from (10.7) by imposing the restriction
![]() $\langle \,f\rangle =0$
, i.e. zero toroidal flux. But do not confuse this zero-flux eigenvalue
with that defined by the boundary condition
$\langle \,f\rangle =0$
, i.e. zero toroidal flux. But do not confuse this zero-flux eigenvalue
with that defined by the boundary condition
![]() $f=0$
. The latter determines a field reversal point analogous to
$f=0$
. The latter determines a field reversal point analogous to
![]() ${\it\theta}=1.2$
in RFPs. In the multipinch, the zero-flux and field reversal
eigenvalues are close together,
${\it\theta}=1.2$
in RFPs. In the multipinch, the zero-flux and field reversal
eigenvalues are close together,
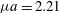 ${\it\mu}a=2.21$
and
${\it\mu}a=2.21$
and
 ${\it\mu}a=2.18$
, respectively (see discussion below).
${\it\mu}a=2.18$
, respectively (see discussion below).
10.1. Nature of the eigenfunctions in multipinch
In the same way that we had to determine which of many eigenfunctions in a cylinder had the lowest energy, we still have to decide whether the lowest eigenvalue in the multipinch is in fact associated with an axisymmetric eigenfunction. In a cylinder the lowest eigenfunction was helical, but in a re-entrant cross-section the reverse may be the case.

Figure 28. (a) Idealised multipinch and (b) toroidal
wavenumber corresponding to the lowest eigenvalue as a function of
![]() ${\it\Delta}$
. (Reproduced with permission from Gimblett
et al. (Reference Gimblett, Hall, Taylor and Turner1987).
Copyright 1987, AIP Publishing LLC.)
${\it\Delta}$
. (Reproduced with permission from Gimblett
et al. (Reference Gimblett, Hall, Taylor and Turner1987).
Copyright 1987, AIP Publishing LLC.)
To see why, consider the extreme case of a multipinch made up of two circular tori,
one above the other, connected only by a narrow slit where they make contact. In this
case an axisymmetric eigenfunction, carrying no net flux, could be constructed from a
circular cylinder solution in each torus, one carrying positive toroidal flux and the
other carrying equal negative flux. To be continuous, the toroidal field would then
have to vanish at the slit – so the two cylinder solutions must have
 ${\it\mu}a\sim 2.4$
, much lower than the helical eigenvalue
${\it\mu}a\sim 2.4$
, much lower than the helical eigenvalue
 ${\it\mu}a\sim 3.11$
. This suggests that the lowest eigenfunction in a multipinch is
axisymmetric, at least when the ‘waist’ is narrow. (It also explains why the field
reversal point is so close to the zero-flux eigenvalue.)
${\it\mu}a\sim 3.11$
. This suggests that the lowest eigenfunction in a multipinch is
axisymmetric, at least when the ‘waist’ is narrow. (It also explains why the field
reversal point is so close to the zero-flux eigenvalue.)
Numerical computations (Gimblett et al.
Reference Gimblett, Hall, Taylor and Turner1987) confirm this picture. Figure 28 shows the toroidal wavenumber of the lowest
eigenfunction for an idealised linear multipinch, with cross-section made up of
circular arcs. When the ‘waist’
![]() ${\it\Delta}$
is comparable with the diameter of the lobes (
${\it\Delta}$
is comparable with the diameter of the lobes (
 ${\it\Delta}/a\sim 1$
so there is essentially no indentation at the waist), the helical
wavelength
${\it\Delta}/a\sim 1$
so there is essentially no indentation at the waist), the helical
wavelength
![]() $2{\rm\pi}/k_{c}$
is
$2{\rm\pi}/k_{c}$
is
![]() ${\sim}10$
times the lobe width. As the waist is narrowed, the wavelength
increases and becomes infinite, that is, the eigenfunction becomes axisymmetric, when
${\sim}10$
times the lobe width. As the waist is narrowed, the wavelength
increases and becomes infinite, that is, the eigenfunction becomes axisymmetric, when
 ${\it\Delta}=0.66$
. (This is somewhat larger than the actual experiment, but its
cross-section is not made up of circular arcs.)
${\it\Delta}=0.66$
. (This is somewhat larger than the actual experiment, but its
cross-section is not made up of circular arcs.)
We can now describe the properties we would expect of relaxed states in the multipinch.
-
(i) For small
 $K/{\it\Psi}^{2}$
(low volt-seconds), the relaxed state will be axisymmetric
and symmetric about the equator/mid-plane, as in figure 27(a). In this state, plasma current is
the same in both lobes and increases with increasing volt-seconds.
$K/{\it\Psi}^{2}$
(low volt-seconds), the relaxed state will be axisymmetric
and symmetric about the equator/mid-plane, as in figure 27(a). In this state, plasma current is
the same in both lobes and increases with increasing volt-seconds. -
(ii) When
 $K/{\it\Psi}^{2}$
, or the volt-seconds, reach a critical value, the relaxed
state becomes a superposition of the axisymmetric state and the
eigenfunction shown in figure 27(b). Therefore it continues to be axisymmetric
but is no longer symmetric about the mid-plane. As the volt-seconds (at
fixed toroidal flux) increase further, more current flows in one lobe and
less in the other, but the total current does not change. Also, this
saturated total current is proportional to the toroidal flux
$K/{\it\Psi}^{2}$
, or the volt-seconds, reach a critical value, the relaxed
state becomes a superposition of the axisymmetric state and the
eigenfunction shown in figure 27(b). Therefore it continues to be axisymmetric
but is no longer symmetric about the mid-plane. As the volt-seconds (at
fixed toroidal flux) increase further, more current flows in one lobe and
less in the other, but the total current does not change. Also, this
saturated total current is proportional to the toroidal flux
 ${\it\Psi}$
.
${\it\Psi}$
.
10.2. Experimental results
The features described above are clearly demonstrated in the experiment. Figure 29 shows the peak plasma current as a function of
the driving transformer voltage
![]() $V_{CB}$
, at fixed
$V_{CB}$
, at fixed
![]() ${\it\Psi}$
. (Plasma current is a measure of
${\it\Psi}$
. (Plasma current is a measure of
![]() ${\it\mu}a$
and
${\it\mu}a$
and
![]() $V_{CB}$
is a rough measure of
$V_{CB}$
is a rough measure of
![]() $K/{\it\Psi}^{2}$
.) Note the following:
$K/{\it\Psi}^{2}$
.) Note the following:

Figure 29. (a) Plasma current versus driving voltage and
(b) variation of saturation current with toroidal flux
in the multipinch. The value
 ${\it\theta}=1.56$
corresponds to
${\it\theta}=1.56$
corresponds to
 ${\it\mu}a=2.42$
here. (Reproduced with permission from La Haye
et al. (Reference La Haye, Jensen, Lee and Ohkawa1986).)
${\it\mu}a=2.42$
here. (Reproduced with permission from La Haye
et al. (Reference La Haye, Jensen, Lee and Ohkawa1986).)
-
(i) At low
 $V_{CB}$
, the current is axisymmetric and symmetric about the
equatorial mid-plane, i.e. equal in the upper and lower lobes, and it
increases with
$V_{CB}$
, the current is axisymmetric and symmetric about the
equatorial mid-plane, i.e. equal in the upper and lower lobes, and it
increases with
 $V_{CB}$
.
$V_{CB}$
. -
(ii) Above a critical
 $V_{CB}$
, the current remains axisymmetric but ceases to be
symmetric about the mid-plane and it no longer increases with
$V_{CB}$
, the current remains axisymmetric but ceases to be
symmetric about the mid-plane and it no longer increases with
 $V_{CB}$
. The total current saturates but more of it flows in one
lobe and less in the other, and this asymmetry increases as
$V_{CB}$
. The total current saturates but more of it flows in one
lobe and less in the other, and this asymmetry increases as
 $V_{CB}$
increases.
$V_{CB}$
increases. -
(iii) The saturation current,
 $I_{sat}$
, is proportional to the toroidal flux – in agreement with
the relaxed-state prediction,
$I_{sat}$
, is proportional to the toroidal flux – in agreement with
the relaxed-state prediction,
 $I_{sat}/{\it\Psi}\propto {\it\mu}a$
(see figure 29
b).
$I_{sat}/{\it\Psi}\propto {\it\mu}a$
(see figure 29
b). -
(iv) The observed proportionality between
 $I_{sat}$
and
$I_{sat}$
and
 ${\it\Psi}$
corresponds to
${\it\Psi}$
corresponds to
 ${\it\mu}a\sim 2.42$
, in reasonable agreement with the theoretical value
${\it\mu}a\sim 2.42$
, in reasonable agreement with the theoretical value
 ${\it\mu}a=2.21$
for the zero-flux eigenvalue.
${\it\mu}a=2.21$
for the zero-flux eigenvalue.
10.3. Flux generation
In fact, all the features of the experiment agree well with the properties calculated
for the relaxed states – except one! According to theory, the total current should
remain at its saturated value indefinitely as
![]() $V_{CB}$
increases beyond the critical value corresponding to
$V_{CB}$
increases beyond the critical value corresponding to
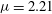 ${\it\mu}=2.21$
. But this is not what happens in the experiment: at some point the
current starts to increase again. The reason for this is that, as
${\it\mu}=2.21$
. But this is not what happens in the experiment: at some point the
current starts to increase again. The reason for this is that, as
![]() $V_{CB}$
increases, less and less current flows in one lobe and more in the
other. This imbalance increases until at some point essentially all the current flows
in one lobe and very little in the other. If current saturation were to continue
beyond this point, as in theory it should, the current would have to
reverse in one lobe. Instead, the discharge dies out in that lobe
and becomes confined to the other, where it acts as a simple toroidal pinch whose
current increases with
$V_{CB}$
increases, less and less current flows in one lobe and more in the
other. This imbalance increases until at some point essentially all the current flows
in one lobe and very little in the other. If current saturation were to continue
beyond this point, as in theory it should, the current would have to
reverse in one lobe. Instead, the discharge dies out in that lobe
and becomes confined to the other, where it acts as a simple toroidal pinch whose
current increases with
![]() $V_{CB}$
.
$V_{CB}$
.
This feature of the multipinch brings out an important aspect of relaxation: it is not a passive decay process. It involves the generation of flux and current by plasma turbulence – as in a turbulent dynamo. When the multipinch reaches the state in which essentially all the current is in one lobe, and any further advance would require reverse current, the ‘dynamo’ is unable to act through the narrow gap from one lobe to the other – so the current remains confined to one lobe.
Finally we should note that current saturation in the multipinch is another example of spontaneous symmetry breaking, as it was in the cylinder. However, the symmetry involved is different in the two systems. In the cylinder it is the axial symmetry that is broken, whereas in the multipinch it is the symmetry about the equatorial plane.
11. Spherical systems I: spheromak
Relaxation also occurs in spherical systems, that is, systems that are not multiply connected as is a torus. This topological change has a profound effect on the nature of the relaxed states (Turner et al. Reference Turner, Goldenbaum, Granneman, Hammer, Hartman, Prono and Taska1983; Taylor Reference Taylor1985, Reference Taylor1986, Reference Taylor1992).
The simplest spherical system is the spheromak, shown in figure 30. This has nested toroidal flux surfaces that may appear similar to those in a toroidal pinch. The crucial difference is that in the spheromak there is no central aperture (no hole in the doughnut) to permit toroidal field coils. This implies the following:
-
(i) Reconnection can occur across the axis so that toroidal flux need not be conserved.
-
(ii) The toroidal field
 $B_{{\it\phi}}$
vanishes everywhere on the boundary. But this does not imply
$B_{{\it\phi}}$
vanishes everywhere on the boundary. But this does not imply
 $q=0$
, as it would in a toroidal system. In fact, in a spheromak
$q=0$
, as it would in a toroidal system. In fact, in a spheromak
 $q$
is remarkably uniform in the relaxed state, with
$q$
is remarkably uniform in the relaxed state, with
 $q=0.825$
on the magnetic axis and
$q=0.825$
on the magnetic axis and
 $q=0.72$
at the wall. The finite value of
$q=0.72$
at the wall. The finite value of
 $q$
at the wall arises because
$q$
at the wall arises because
 $q({\it\psi})$
is an average over a flux surface and near the wall this
involves taking a limit in which both
$q({\it\psi})$
is an average over a flux surface and near the wall this
involves taking a limit in which both
 $B_{toroidal}$
and
$B_{toroidal}$
and
 $B_{poloidal}$
tend to zero at the poles, with the ratio leading to a finite
$B_{poloidal}$
tend to zero at the poles, with the ratio leading to a finite
 $q({\it\Psi})$
.
$q({\it\Psi})$
.

Figure 30. Schematic of a spheromak configuration (from Taylor Reference Taylor1986).
As there can be no transformer core through a spheromak, we cannot use this to create a plasma. Instead, there are three main techniques for creating a spheromak:
-
(i) coaxial gun injection,
-
(ii) combined
 ${\it\theta}{-}z$
discharges and
${\it\theta}{-}z$
discharges and -
(iii) an inductive flux core.
These are illustrated in figure 31, and the details of their operation can be found in Taylor (Reference Taylor1986) and references therein.

Figure 31. Methods to create a spheromak discharge: (a) by plasma gun
(reproduced with permission from Turner et al.
Reference Turner, Goldenbaum, Granneman, Hammer, Hartman, Prono and Taska1983, copyright 1983, AIP Publishing
LLC), (b) by combined
![]() ${\it\theta}{-}z$
discharge (reprinted with permission from Goldenbaum
et al.
Reference Goldenbaum, Irby, Chong and Hart1980, copyright 1980 by the American
Physical Society) and (c) by inductive flux core in S-1
(reprinted with permission from Yamada et al.
Reference Yamada, Furth, Hsu, Janos, Jardin, Okabayashu, Sinnis, Stix and Yamazaki1981, copyright 1981 by the American
Physical Society).
${\it\theta}{-}z$
discharge (reprinted with permission from Goldenbaum
et al.
Reference Goldenbaum, Irby, Chong and Hart1980, copyright 1980 by the American
Physical Society) and (c) by inductive flux core in S-1
(reprinted with permission from Yamada et al.
Reference Yamada, Furth, Hsu, Janos, Jardin, Okabayashu, Sinnis, Stix and Yamazaki1981, copyright 1981 by the American
Physical Society).
11.1. Relaxed states of a spheromak
The helicity
 $K=\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is conserved in a spheromak during relaxation (see § 7.1), and the relaxed state satisfies
$K=\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
is conserved in a spheromak during relaxation (see § 7.1), and the relaxed state satisfies
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})={\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})={\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}.\end{eqnarray}$$
Now, we recall that in a torus there were two invariants,
![]() $K$
and
$K$
and
![]() ${\it\Psi}$
, which were just sufficient to determine the relaxed state.
However, in a spheromak, we have only one invariant, the helicity
${\it\Psi}$
, which were just sufficient to determine the relaxed state.
However, in a spheromak, we have only one invariant, the helicity
![]() $K$
. The toroidal flux is no longer invariant because annihilation of
flux can occur across the axis of symmetry. How, then, can the relaxed state be
unique in a spheromak?
$K$
. The toroidal flux is no longer invariant because annihilation of
flux can occur across the axis of symmetry. How, then, can the relaxed state be
unique in a spheromak?
The key to this question is that in a torus there were two independent loop integrals
on the surface of the torus:
![]() $\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}$
, the flux through the ‘hole’ in the torus; and
$\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}$
, the flux through the ‘hole’ in the torus; and
 $\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}={\it\Psi}$
, the toroidal flux inside the torus. But in a spheromak, being
simply connected, all loop integrals on the surface are identical. In fact, since
there is no flux through the boundary, they are all zero. Apart from an irrelevant
gauge transformation this is equivalent to
$\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}={\it\Psi}$
, the toroidal flux inside the torus. But in a spheromak, being
simply connected, all loop integrals on the surface are identical. In fact, since
there is no flux through the boundary, they are all zero. Apart from an irrelevant
gauge transformation this is equivalent to
![]() $\boldsymbol{A}\equiv 0$
on the boundary of a spheromak. But this is just the
spheromak eigenvalue condition!
$\boldsymbol{A}\equiv 0$
on the boundary of a spheromak. But this is just the
spheromak eigenvalue condition!
Hence for a spheromak, the only relaxed state is the lowest
eigenfunction: the eigenvalue determines
![]() ${\it\mu}$
and the field amplitude is determined by the sole invariant
${\it\mu}$
and the field amplitude is determined by the sole invariant
![]() $K$
. This means that, apart from a scale factor, the relaxed
state in a spheromak is unique and entirely determined by the shape of the
container.
$K$
. This means that, apart from a scale factor, the relaxed
state in a spheromak is unique and entirely determined by the shape of the
container.
11.2. Spheromak eigenfunctions
Axisymmetric eigenfunctions in a spheromak are easily found. The field is again written as (10.1) and the eigenvalue problem reduces to
 $$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}{\it\chi}=0,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}^{+}{\it\chi}+{\it\mu}^{2}{\it\chi}=0,\end{eqnarray}$$
with
![]() ${\it\chi}=0$
on the boundary, as in (10.6).
${\it\chi}=0$
on the boundary, as in (10.6).
In a sphere of radius
![]() $a$
, the eigenfunction, in spherical coordinates (
$a$
, the eigenfunction, in spherical coordinates (
![]() ${\it\rho},{\it\theta},{\it\phi}$
), is
${\it\rho},{\it\theta},{\it\phi}$
), is
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\rho}}=2B_{0}\left[\frac{\,j_{1}({\it\mu}{\it\rho})}{{\it\mu}{\it\rho}}\right]\cos {\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\rho}}=2B_{0}\left[\frac{\,j_{1}({\it\mu}{\it\rho})}{{\it\mu}{\it\rho}}\right]\cos {\it\theta}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{{\it\theta}}=B_{0}[\,j_{1}({\it\mu}{\it\rho})]\sin {\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{{\it\theta}}=B_{0}[\,j_{1}({\it\mu}{\it\rho})]\sin {\it\theta}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\phi}}=-B_{0}\frac{\text{d}}{\text{d}{\it\rho}}({\it\rho}j_{1}({\it\mu}{\it\rho}))\sin {\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\phi}}=-B_{0}\frac{\text{d}}{\text{d}{\it\rho}}({\it\rho}j_{1}({\it\mu}{\it\rho}))\sin {\it\theta}, & \displaystyle\end{eqnarray}$$
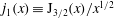 $j_{1}(x)\equiv \text{J}_{3/2}(x)/x^{1/2}$
, and the eigenvalue is
$j_{1}(x)\equiv \text{J}_{3/2}(x)/x^{1/2}$
, and the eigenvalue is
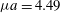 ${\it\mu}a=4.49$
.
${\it\mu}a=4.49$
.
In a cylindrical container of height
![]() $h$
and radius
$h$
and radius
![]() $a$
(which, of course, is topologically spherical), the eigenfunction,
in cylindrical coordinates
$a$
(which, of course, is topologically spherical), the eigenfunction,
in cylindrical coordinates
![]() $(r,{\it\theta},z)$
, is
$(r,{\it\theta},z)$
, is
 $$\begin{eqnarray}\displaystyle & B_{r}=-B_{0}k\text{J}_{1}(lr)\cos kz, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{r}=-B_{0}k\text{J}_{1}(lr)\cos kz, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{{\it\phi}}=B_{0}{\it\mu}\text{J}_{1}(lr)\sin kz, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{{\it\phi}}=B_{0}{\it\mu}\text{J}_{1}(lr)\sin kz, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & B_{z}=B_{0}k\text{J}_{0}(lr)\sin kz, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{z}=B_{0}k\text{J}_{0}(lr)\sin kz, & \displaystyle\end{eqnarray}$$
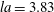 $la=3.83$
and the eigenvalue is
$la=3.83$
and the eigenvalue is
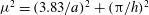 ${\it\mu}^{2}=(3.83/a)^{2}+({\rm\pi}/h)^{2}$
.
${\it\mu}^{2}=(3.83/a)^{2}+({\rm\pi}/h)^{2}$
.
11.3. Experimental data
In figure 32 the poloidal and toroidal field
profiles given by (11.8) are
compared with those measured in the BETA II experiment (Turner
et al.
Reference Turner, Goldenbaum, Granneman, Hammer, Hartman, Prono and Taska1983). This has a cylindrical flux conserver
with
![]() $h/a\sim 1$
and a plasma created by a coaxial gun (see figure 31
a). The agreement is reasonable, particularly in view of the complex
way the plasma is created, and it is particularly significant that the measured
profiles remain essentially unchanged as the magnetic energy decays to
$h/a\sim 1$
and a plasma created by a coaxial gun (see figure 31
a). The agreement is reasonable, particularly in view of the complex
way the plasma is created, and it is particularly significant that the measured
profiles remain essentially unchanged as the magnetic energy decays to
![]() ${\sim}1/8$
of its initial value. (Recall that the relaxed state of a spheromak
is determined solely by the shape of the container.)
${\sim}1/8$
of its initial value. (Recall that the relaxed state of a spheromak
is determined solely by the shape of the container.)

Figure 32. Magnetic field profiles in the BETA II spheromak. (a) Poloidal field and (b) toroidal field. Experimental measurements are shown as squares; the solid line is the theoretical prediction. (Reproduced with permission from Turner et al. (Reference Turner, Goldenbaum, Granneman, Hammer, Hartman, Prono and Taska1983). Copyright 1983, AIP Publishing LLC.)
The near-uniformity of
![]() ${\it\mu}$
in a relaxed state is supported by the measurements shown in
figure 33, taken on the S-1 spheromak, which
has an ellipsoidal flux conserver and a plasma produced by an inductive flux core
(Hart et al.
Reference Hart, Janos, Meyerhofer and Yamada1986). Figure 33(a) shows the ratio of poloidal current to poloidal
flux across the mid-plane. The observations lie on a straight line whose slope agrees
remarkably well with the computed value of
${\it\mu}$
in a relaxed state is supported by the measurements shown in
figure 33, taken on the S-1 spheromak, which
has an ellipsoidal flux conserver and a plasma produced by an inductive flux core
(Hart et al.
Reference Hart, Janos, Meyerhofer and Yamada1986). Figure 33(a) shows the ratio of poloidal current to poloidal
flux across the mid-plane. The observations lie on a straight line whose slope agrees
remarkably well with the computed value of
![]() ${\it\mu}\sim 5.5$
. Figure 33(b) shows how the ratio
${\it\mu}\sim 5.5$
. Figure 33(b) shows how the ratio
 $J/B={\it\mu}$
on the mid-plane changes from an initial highly non-uniform profile
(dashed line) to a much more uniform profile (solid line) after relaxation.
$J/B={\it\mu}$
on the mid-plane changes from an initial highly non-uniform profile
(dashed line) to a much more uniform profile (solid line) after relaxation.
Figure 33. (a) Poloidal current versus poloidal flux and
(b) measured profile of
![]() ${\it\mu}(r)$
in S-1 spheromak. (Reproduced with permission from Hart
et al. (Reference Hart, Janos, Meyerhofer and Yamada1986).
Copyright 1986, AIP Publishing LLC.)
${\it\mu}(r)$
in S-1 spheromak. (Reproduced with permission from Hart
et al. (Reference Hart, Janos, Meyerhofer and Yamada1986).
Copyright 1986, AIP Publishing LLC.)
Finally, figure 34 provides the most striking
evidence for relaxation. This shows the evolution of the poloidal and toroidal
fluxes, and of
![]() $q$
on the magnetic axis, during a plasma discharge in the S-1
spheromak (Janos et al.
Reference Janos, Hart and Yamada1985a
,Reference Janos, Hart, Nam and Yamada
b
). Figure 34(c) shows
that
$q$
on the magnetic axis, during a plasma discharge in the S-1
spheromak (Janos et al.
Reference Janos, Hart and Yamada1985a
,Reference Janos, Hart, Nam and Yamada
b
). Figure 34(c) shows
that
![]() $q$
rises rapidly from a small initial value and becomes close to that
predicted for the relaxed state. It is then essentially constant for the remainder of
the experiment. This rapid rise in
$q$
rises rapidly from a small initial value and becomes close to that
predicted for the relaxed state. It is then essentially constant for the remainder of
the experiment. This rapid rise in
![]() $q$
is accompanied by an increase in toroidal flux (see figure 34
b) and a decrease in poloidal flux (see figure 34
a), during a period when there is strong plasma activity. This again
shows that relaxation is not simply a passive decay but involves the creation and
destruction of magnetic flux by plasma turbulence – or in this case the conversion of
poloidal flux into toroidal flux.
$q$
is accompanied by an increase in toroidal flux (see figure 34
b) and a decrease in poloidal flux (see figure 34
a), during a period when there is strong plasma activity. This again
shows that relaxation is not simply a passive decay but involves the creation and
destruction of magnetic flux by plasma turbulence – or in this case the conversion of
poloidal flux into toroidal flux.

Figure 34. Time dependence of magnetic fields in S-1 spheromak – see text for details. (Reproduced with permission from Janos et al. (Reference Janos, Hart and Yamada1985a ).)
12. Spherical systems II: flux core spheromak
An interesting development of the spheromak is a configuration obtained from it by introducing a central core of externally produced magnetic flux along the axis, which enters through one polar cap and leaves through the other (see figure 35). This ‘flux core spheromak’ again has nested toroidal magnetic surfaces that resemble those in a toroidal pinch, but there is only plasma in the central core and reconnection can occur across the axis. Consequently the toroidal flux is again not conserved in this system.

Figure 35. Schematic of a flux core spheromak (from Taylor Reference Taylor1986).
12.1. Relative helicity
In the flux core spheromak, the plasma boundary is not a completely closed flux surface, and we noted earlier that in this case our definition of helicity is not gauge-invariant. This is more of a conceptual problem than a practical one, and can be overcome by introducing a modified definition of helicity.
The most intuitive modification is to imagine that the flux leaving or entering the
boundary is extended outside as a vacuum field, where
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}=0$
. Then the integral
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}=0$
. Then the integral
 $\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
, inside plus outside the sphere, is
gauge-invariant. If the boundary of the sphere is a perfect conductor, the normal
component of
$\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
, inside plus outside the sphere, is
gauge-invariant. If the boundary of the sphere is a perfect conductor, the normal
component of
![]() $\boldsymbol{B}$
is ‘frozen in’ and changes inside the sphere do not affect the
hypothetical field outside. Therefore, the difference in
$\boldsymbol{B}$
is ‘frozen in’ and changes inside the sphere do not affect the
hypothetical field outside. Therefore, the difference in
 $\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
for two configurations that differ inside the sphere but have the
same
$\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}$
for two configurations that differ inside the sphere but have the
same
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{B}$
on the surface (and therefore the same hypothetical extension
field) is also well-defined and gauge-invariant. This is sometimes called the
relative helicity,
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{B}$
on the surface (and therefore the same hypothetical extension
field) is also well-defined and gauge-invariant. This is sometimes called the
relative helicity,
![]() $K_{R}$
.
$K_{R}$
.
Note that
![]() $K_{R}$
must include the integral both inside and outside the sphere in
order to be gauge-invariant, even though physically the latter does not change. This
requirement reflects the fact that helicity is not a local quantity: it can be
transferred from inside to outside by a gauge transformation!
$K_{R}$
must include the integral both inside and outside the sphere in
order to be gauge-invariant, even though physically the latter does not change. This
requirement reflects the fact that helicity is not a local quantity: it can be
transferred from inside to outside by a gauge transformation!
The relative helicity satisfies
 $$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=-2\int _{interior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}-2\int _{exterior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=-2\int _{interior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}-2\int _{exterior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}.\end{eqnarray}$$
The exterior field does not change, therefore
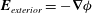 $\boldsymbol{E}_{exterior}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
and
$\boldsymbol{E}_{exterior}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
and
 $$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=-2\int _{interior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}+2\oint _{S}{\it\phi}\,\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{S}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=-2\int _{interior}\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}+2\oint _{S}{\it\phi}\,\boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{S}.\end{eqnarray}$$
In the interior
 $\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}=0$
and the first integral vanishes. If the potential
$\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}=0$
and the first integral vanishes. If the potential
![]() ${\it\phi}$
is constant over the surface, the last integral is also zero.
${\it\phi}$
is constant over the surface, the last integral is also zero.
The purpose of introducing the flux core spheromak here is that it demonstrates another method of injecting helicity, in this case by a static voltage. If, instead of a uniform potential on the surface, one polar cap is held at a different potential from the other, helicity will be injected at a rate
 $$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=2V_{p}{\it\Psi}_{p},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K_{R}}{\text{d}t}=2V_{p}{\it\Psi}_{p},\end{eqnarray}$$
where
![]() $V_{p}$
is the voltage between the polar caps and
$V_{p}$
is the voltage between the polar caps and
![]() ${\it\Psi}_{p}$
is the flux through them (Taylor Reference Taylor1986).
${\it\Psi}_{p}$
is the flux through them (Taylor Reference Taylor1986).
12.2. Relaxed states of flux core spheromak
The relaxed state of the flux core spheromak satisfies the usual equation (11.1) and the relative helicity
![]() $K_{R}$
is invariant, but the appropriate solution is selected in a
different way. In fact, a flux core spheromak can be operated in several ways. If the
plasma relaxes from an initial state with given helicity
$K_{R}$
is invariant, but the appropriate solution is selected in a
different way. In fact, a flux core spheromak can be operated in several ways. If the
plasma relaxes from an initial state with given helicity
![]() $K_{R}$
, and with fixed flux
$K_{R}$
, and with fixed flux
![]() ${\it\Psi}_{p}$
through the polar caps, then
${\it\Psi}_{p}$
through the polar caps, then
![]() ${\it\mu}$
is specified by
${\it\mu}$
is specified by
![]() $K_{R}/{\it\Psi}_{p}^{2}$
somewhat in the same way as in a toroidal pinch (see figure 36 and § 9).
However, this is only correct if the polar caps can provide whatever current is
required by the resulting relaxed state. If this is not so, a voltage sheath would
appear at the polar caps and the resulting voltage drop would reduce the helicity
according to (12.3). This leads to
another way of operating a flux core spheromak. If one polar cap is insulated from
the other and connected to an external circuit that maintains a fixed current
$K_{R}/{\it\Psi}_{p}^{2}$
somewhat in the same way as in a toroidal pinch (see figure 36 and § 9).
However, this is only correct if the polar caps can provide whatever current is
required by the resulting relaxed state. If this is not so, a voltage sheath would
appear at the polar caps and the resulting voltage drop would reduce the helicity
according to (12.3). This leads to
another way of operating a flux core spheromak. If one polar cap is insulated from
the other and connected to an external circuit that maintains a fixed current
![]() $I_{p}$
, then in the relaxed state
$I_{p}$
, then in the relaxed state
 ${\it\mu}=I_{p}/{\it\Psi}_{p}$
. This provides a method for external control of a flux core
spheromak (see figure 37).
${\it\mu}=I_{p}/{\it\Psi}_{p}$
. This provides a method for external control of a flux core
spheromak (see figure 37).

Figure 36. Analogy between tokamak and flux core spheromak.

Figure 37. Set-up to control relaxed state of flux core spheromak externally.
The relaxed states of a flux core spheromak are calculated in a similar way to those
in a simple spheromak. Only the boundary conditions are different. Instead of
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
on the boundary, it now has a fixed value on the polar caps and is
zero elsewhere. A typical computed field profile is shown in figure 38. Analytic solutions for an idealised flux core
system in which the polar caps are shrunk to a point while retaining finite flux
through them are shown in figure 39. These show
the changes that occur as the current through the polar caps, and therefore
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}=0$
on the boundary, it now has a fixed value on the polar caps and is
zero elsewhere. A typical computed field profile is shown in figure 38. Analytic solutions for an idealised flux core
system in which the polar caps are shrunk to a point while retaining finite flux
through them are shown in figure 39. These show
the changes that occur as the current through the polar caps, and therefore
![]() ${\it\mu}$
, is increased. When
${\it\mu}$
, is increased. When
![]() ${\it\mu}$
is much less than the lowest spheromak eigenvalue (
${\it\mu}$
is much less than the lowest spheromak eigenvalue (
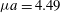 ${\it\mu}a=4.49$
), the externally linked flux and current form a large part of the
total flux and current. But as
${\it\mu}a=4.49$
), the externally linked flux and current form a large part of the
total flux and current. But as
![]() ${\it\mu}$
approaches the eigenvalue, the ratio of self-generated flux to
externally linked flux increases indefinitely, and the externally linked flux becomes
confined to a slim pencil along the axis of symmetry. This situation would constitute
an extreme example of the generation of fields by the relaxation process. At the
critical point all the fields would, in theory, be generated by the
plasma itself.
${\it\mu}$
approaches the eigenvalue, the ratio of self-generated flux to
externally linked flux increases indefinitely, and the externally linked flux becomes
confined to a slim pencil along the axis of symmetry. This situation would constitute
an extreme example of the generation of fields by the relaxation process. At the
critical point all the fields would, in theory, be generated by the
plasma itself.

Figure 38. Calculated field in a flux core spheromak,
 ${\it\mu}a=4.09$
(from Taylor Reference Taylor1986).
${\it\mu}a=4.09$
(from Taylor Reference Taylor1986).

Figure 39. Evolution of analytic field profiles in an idealised flux core spheromak at
various values of
![]() ${\it\mu}a$
: (a)
${\it\mu}a$
: (a)
 ${\it\mu}a=0.001$
, (b)
${\it\mu}a=0.001$
, (b)
 ${\it\mu}a=2.25$
, (c)
${\it\mu}a=2.25$
, (c)
 ${\it\mu}a=2.70$
, (d)
${\it\mu}a=2.70$
, (d)
 ${\it\mu}a=3.00$
, (e)
${\it\mu}a=3.00$
, (e)
 ${\it\mu}a=4.00$
, ( f)
${\it\mu}a=4.00$
, ( f)
 ${\it\mu}a=4.14$
and (g)
${\it\mu}a=4.14$
and (g)
 ${\it\mu}a=5.00$
. (Reproduced with permission from Turner (Reference Turner1984). Copyright 1984, AIP Publishing
LLC.)
${\it\mu}a=5.00$
. (Reproduced with permission from Turner (Reference Turner1984). Copyright 1984, AIP Publishing
LLC.)
12.3. Experimental control of relaxed states
In a simple spheromak the field in the relaxed state will normally decay at the
resistive diffusion rate (while retaining its profile). However, as we noted above,
if the polar flux
![]() ${\it\Psi}_{p}$
and the polar current
${\it\Psi}_{p}$
and the polar current
![]() $I_{p}$
in a flux core spheromak are maintained, it should be possible to
maintain its relaxed state at any amplitude and any
$I_{p}$
in a flux core spheromak are maintained, it should be possible to
maintain its relaxed state at any amplitude and any
 ${\it\mu}=K_{R}/{\it\Psi}_{p}^{2}$
below the lowest eigenvalue. This idea is the basis for the
experiments described below.
${\it\mu}=K_{R}/{\it\Psi}_{p}^{2}$
below the lowest eigenvalue. This idea is the basis for the
experiments described below.
A somewhat distorted form of flux core spheromak, as shown in figure 40, has been extensively investigated at Los Alamos (CTX) (Jarboe et al. Reference Jarboe, Barnes, Platts and Wright1985; Barnes et al. Reference Barnes, Fernández, Henins, Hoida, Jarboe, Knox, Marklin and McKenna1986) and at UMIST (SPHEX) (Kitson & Browning Reference Kitson and Browning1990). The plasma in CTX is created by a plasma gun (on the left of the diagram). This injects plasma into a container, or ‘flux conserver’, at the right of the figure. If we concentrate attention on the flux conserver, we can see that there is a core of flux (shaded), which passes from the inner electrode of the gun, along the axis of the plasma in the flux conserver and then round the outside of the plasma back to the outer electrode of the gun. From the plasma viewpoint, the gun voltage appears across the flux core and acts as if it were between polar caps. This voltage can sustain the configuration against resistive decay for many times the usual resistive diffusion time.

Figure 40. Sustained configuration in CTX experiment (from Jarboe et al. Reference Jarboe, Barnes, Platts and Wright1985).
At this point we should note the time scales involved in this discussion:
-
(i) Relaxation time. This is much faster than the resistive diffusion time
 $a^{2}/{\it\eta}$
, and often close to the Alfvén time. This leads to the
relaxed state. The helicity
$a^{2}/{\it\eta}$
, and often close to the Alfvén time. This leads to the
relaxed state. The helicity
 $K_{R}$
is invariant on this time scale.
$K_{R}$
is invariant on this time scale. -
(ii) The resistive diffusion time
 ${\sim}a^{2}/{\it\eta}$
. This is the time scale on which
${\sim}a^{2}/{\it\eta}$
. This is the time scale on which
 $K_{R}$
and the relaxed state itself decays, if it is not
maintained by some external means.
$K_{R}$
and the relaxed state itself decays, if it is not
maintained by some external means. -
(iii) The sustainment time. This is the time, longer than
 $a^{2}/{\it\eta}$
, on which the discharge can be maintained in its relaxed
state by an external voltage.
$a^{2}/{\it\eta}$
, on which the discharge can be maintained in its relaxed
state by an external voltage.
12.4. The kinked Z-pinch
Once it was realised that a flux core spheromak could be maintained in the ways
described above, it was found that they could also be created and maintained in more
exotic configurations. One of these was the ‘kinked Z-pinch’ helicity source (Jarboe
et al.
Reference Jarboe, Barnes, Platts and Wright1985; Fernández et al.
Reference Fernández, Wright, Marklin, Platts and Jarboe1989), shown in figure 41. In a highly idealised way, we can regard this device as
creating a sequence of relaxed states in each of the three regions marked 1, 2 and 3.
In region 1, we have a simple linear pinch maintained by the electrodes. Insofar as
it is relaxed,
![]() ${\it\mu}$
would be set by the ratio of the current
${\it\mu}$
would be set by the ratio of the current
![]() $I_{s}$
and flux
$I_{s}$
and flux
![]() ${\it\Psi}_{s}$
at the electrodes,
${\it\Psi}_{s}$
at the electrodes,
 ${\it\mu}_{1}=I_{s}/{\it\Psi}_{s}$
. In region 2, we have a helical relaxed state of a circular
cylinder, with no net current or flux. If the cylinder were long, this would be the
${\it\mu}_{1}=I_{s}/{\it\Psi}_{s}$
. In region 2, we have a helical relaxed state of a circular
cylinder, with no net current or flux. If the cylinder were long, this would be the
![]() $m=1$
,
$m=1$
,
 $ka=1.23$
eigenfunction, which we discussed in connection with the
cylindrical pinch. This would have
$ka=1.23$
eigenfunction, which we discussed in connection with the
cylindrical pinch. This would have
 ${\it\mu}_{2}a_{2}\sim 3.11$
as calculated in § 9.1.
Finally, in region 3, we would have a spheromak with
${\it\mu}_{2}a_{2}\sim 3.11$
as calculated in § 9.1.
Finally, in region 3, we would have a spheromak with
![]() ${\it\mu}_{3}a_{3}$
, defined solely by the size and shape of the flux conserver (see
§ 11.2).
${\it\mu}_{3}a_{3}$
, defined solely by the size and shape of the flux conserver (see
§ 11.2).

Figure 41. Illustration of kinked Z-pinch source.
Now, recall from § 9.1 that the energy for a
given helicity in a relaxed state increases with
![]() ${\it\mu}$
. Consequently, it will be energetically favourable for the
discharge to pass from region 1 to 2 and then into 3 if, and only if,
${\it\mu}$
. Consequently, it will be energetically favourable for the
discharge to pass from region 1 to 2 and then into 3 if, and only if,
 $$\begin{eqnarray}{\it\mu}_{1}>{\it\mu}_{2}>{\it\mu}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\mu}_{1}>{\it\mu}_{2}>{\it\mu}_{3}.\end{eqnarray}$$
In fact,
![]() ${\it\mu}_{2}>{\it\mu}_{3}$
is set by the dimensions of the apparatus, but
${\it\mu}_{2}>{\it\mu}_{3}$
is set by the dimensions of the apparatus, but
![]() ${\it\mu}_{1}$
can be controlled externally and we can expect there to be a
threshold for the successful injection of the spheromak into the
flux conserver, set by
${\it\mu}_{1}$
can be controlled externally and we can expect there to be a
threshold for the successful injection of the spheromak into the
flux conserver, set by
 $$\begin{eqnarray}\frac{I_{s}}{{\it\Psi}_{s}}={\it\mu}_{1}>{\it\mu}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{I_{s}}{{\it\Psi}_{s}}={\it\mu}_{1}>{\it\mu}_{2}.\end{eqnarray}$$
Such a threshold does seem to occur, as can be seen in figure 42, which shows a ‘figure of merit’ for the
spheromak created in the flux conserver. This is roughly proportional to its total
helicity. Figure 42(a) is for
a 20 cm radius entrance cylinder, whilst figure 42(b) is for a 17 cm radius entrance cylinder. It is
clear from these figures that there is no significant helicity input into the flux
conserver unless
 ${\it\mu}_{1}>13~\text{m}^{-1}$
in (a), and
${\it\mu}_{1}>13~\text{m}^{-1}$
in (a), and
 ${\it\mu}_{1}>14~\text{m}^{-1}$
in (b). The theoretical threshold for a long
cylinder would be
${\it\mu}_{1}>14~\text{m}^{-1}$
in (b). The theoretical threshold for a long
cylinder would be
 ${\sim}15.6~\text{m}^{-1}$
for a 20 cm entrance radius.
${\sim}15.6~\text{m}^{-1}$
for a 20 cm entrance radius.

Figure 42. Spheromak figure of merit
![]() ${\it\kappa}$
versus
${\it\kappa}$
versus
![]() ${\it\lambda}_{e}\equiv {\it\mu}$
. (Reproduced with permission from Fernández
et al. (Reference Fernández, Wright, Marklin, Platts and Jarboe1989).
Copyright 1989, AIP Publishing LLC.)
${\it\lambda}_{e}\equiv {\it\mu}$
. (Reproduced with permission from Fernández
et al. (Reference Fernández, Wright, Marklin, Platts and Jarboe1989).
Copyright 1989, AIP Publishing LLC.)
13. Helicity injection
As we have seen in several situations, because a relaxed state is completely determined
by the helicity
![]() $K$
and flux
$K$
and flux
![]() ${\it\Psi}$
, it can be maintained for longer than the resistive decay time if
${\it\Psi}$
, it can be maintained for longer than the resistive decay time if
![]() $K$
and
$K$
and
![]() ${\it\Psi}$
can be controlled externally.
${\it\Psi}$
can be controlled externally.
In a toroidal system there is no difficulty in principle maintaining
![]() ${\it\Psi}_{tor}$
by the usual toroidal field coils, and in (7.25) we observed that
${\it\Psi}_{tor}$
by the usual toroidal field coils, and in (7.25) we observed that
 $$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=2V_{loop}{\it\Psi}_{tor},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=2V_{loop}{\it\Psi}_{tor},\end{eqnarray}$$
apparently giving control over
![]() $K$
. But unfortunately
$K$
. But unfortunately
![]() $V_{loop}$
itself can be maintained only for a short time – limited by the
volt-seconds available from the driving transformer. However, an oscillating
$V_{loop}$
itself can be maintained only for a short time – limited by the
volt-seconds available from the driving transformer. However, an oscillating
![]() $V_{loop}$
could be maintained, and if
$V_{loop}$
could be maintained, and if
![]() ${\it\Psi}_{tor}$
is simultaneously modulated in the appropriate phase, there is an
average input of helicity
${\it\Psi}_{tor}$
is simultaneously modulated in the appropriate phase, there is an
average input of helicity
 $$\begin{eqnarray}\left\langle \frac{\text{d}K}{\text{d}t}\right\rangle \sim \hat{V}_{loop}\hat{{\it\Psi}}_{tor}\cos {\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}\left\langle \frac{\text{d}K}{\text{d}t}\right\rangle \sim \hat{V}_{loop}\hat{{\it\Psi}}_{tor}\cos {\it\theta},\end{eqnarray}$$
where
![]() $\hat{V}_{loop}$
and
$\hat{V}_{loop}$
and
![]() $\hat{{\it\Psi}}_{tor}$
are the oscillation and modulation amplitudes, and
$\hat{{\it\Psi}}_{tor}$
are the oscillation and modulation amplitudes, and
![]() ${\it\theta}$
is the phase difference between them.
${\it\theta}$
is the phase difference between them.
If this method is to have any chance of success, the plasma relaxation time must be less than the period of oscillation (so that the plasma stays close to its relaxed state) and the period of oscillation must be much less than the resistive decay time, so that there is negligible decay between each cycle.
This method of helicity injection, which is also known as ‘oscillating field current
drive’ (OFCD), was attempted on the ZT-40M experiment (Schoenberg
et al.
Reference Schoenberg, Ingraham, Munson, Weber, Baker, Gribble, Howell, Miller, Reass, Schofield, Shinohara and Wurden1988) with limited success. In part this was due
to the small amplitudes of
![]() $V_{loop}$
and
$V_{loop}$
and
![]() ${\it\Psi}_{tor}$
that were available, but a more fundamental obstacle is that the
process disturbs the plasma equilibrium and creates serious losses by
‘modulation-enhanced plasma–wall interaction’.
${\it\Psi}_{tor}$
that were available, but a more fundamental obstacle is that the
process disturbs the plasma equilibrium and creates serious losses by
‘modulation-enhanced plasma–wall interaction’.
In a flux core spheromak we saw that a voltage
![]() $V_{p}$
applied to the polar caps injects helicity at a rate
$V_{p}$
applied to the polar caps injects helicity at a rate
 $$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=2V_{p}{\it\Psi}_{p},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}K}{\text{d}t}=2V_{p}{\it\Psi}_{p},\end{eqnarray}$$
where
![]() ${\it\Psi}_{p}$
is the flux linking the polar caps. This method of injection was
successfully used in the CTX and other experiments, described in § 12.3.
${\it\Psi}_{p}$
is the flux linking the polar caps. This method of injection was
successfully used in the CTX and other experiments, described in § 12.3.
13.1. Spheromak injection into tokamak
A remarkable application of helicity injection is the attempt (Brown & Bellan
Reference Brown and Bellan1990) to influence the current in a tokamak
by injecting helicity in the form of small spheromaks from a coaxial gun in a side
arm into the main torus! This is illustrated in figure 43. As in the previous discussions, a small spheromak is created in the
mouth of the gun and moves into the main tokamak chamber. To understand the
observations, one must recall that helicity is a pseudo-scalar and therefore can be
right-handed or left-handed. The handedness is related to the sign of
![]() ${\it\mu}$
, that is, to the relative directions of
${\it\mu}$
, that is, to the relative directions of
![]() $\boldsymbol{J}$
and
$\boldsymbol{J}$
and
![]() $\boldsymbol{B}$
.
$\boldsymbol{B}$
.

Figure 43. Schematic of spheromak injection into ENCORE tokamak at Caltech. (Reproduced with permission from Brown & Bellan (Reference Brown and Bellan1990). Copyright 1990, AIP Publishing LLC.)
One can set up the main tokamak discharge with either right- or left-handed helicity by reversing the direction of the toroidal magnetic field, and one can create spheromaks with either right- or left-handed helicity by reversing the polarity of the gun voltage. Therefore, there are four permutations of the experiment:
-
(a) L-hand spheromak injected into L-hand tokamak,
-
(b) L-hand spheromak injected into R-hand tokamak,
-
(c) R-hand spheromak injected into R-hand tokamak,
-
(d) R-hand spheromak injected into L-hand tokamak.
The effect on the tokamak current of injecting the spheromak for the four cases is shown in figure 44. The dotted line in (a) shows the behaviour when there is no spheromak injection. It can be seen that when the injected spheromak and the tokamak have the same chirality (cases (a) and (c)), there is a small spike in the tokamak current. Conversely, when the spheromak and tokamak have opposite helicity (cases (b) and (d)), there is a small drop in the tokamak current. In all four cases the initial rise or drop in current is followed by a rapid decay. This is thought to be due to the cooling of the main plasma by the large amount of cold gas that accompanies the spheromak from the coaxial gun.

Figure 44. Effect on tokamak current of spheromak injection – see text for details. (Reproduced with permission from Brown & Bellan (Reference Brown and Bellan1990). Copyright 1990, AIP Publishing LLC.)
13.2. Wave injection
Another, untried, method of helicity injection is by plasma waves (Mett & Tataronis Reference Mett and Tataronis1989; Taylor Reference Taylor1989; Mett & Taylor Reference Mett and Taylor1992). One might envisage doing this by means of an antenna similar to those used for plasma heating.
Helicity injection by waves is hard to visualise (but see Chan
et al.
Reference Chan, Miller and Ohkawa1990). We have previously emphasised that
helicity is a non-local quantity – the linking of lines of force – and it is
difficult to relate this to wave motion. In fact, this process is more usually
described as ‘current drive’, but it is interesting to see the connection with
helicity. There are, of course, many types of plasma wave, but we will consider only
the simplest – waves in a uniform plasma immersed in a uniform magnetic field
 $\boldsymbol{B}=(0,0,\boldsymbol{B}_{0})$
. However, this already illustrates some of the conceptual
problems.
$\boldsymbol{B}=(0,0,\boldsymbol{B}_{0})$
. However, this already illustrates some of the conceptual
problems.
We start from what looks like a continuity equation for
![]() $\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
,
$\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
,
 $$\begin{eqnarray}\frac{\partial }{\partial t}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{Q}+2(\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B})=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial }{\partial t}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{Q}+2(\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B})=0,\end{eqnarray}$$
where
 $\boldsymbol{Q}={\it\phi}\boldsymbol{B}+\boldsymbol{E}\times \boldsymbol{A}$
. For a plasma with an Ohm’s law
$\boldsymbol{Q}={\it\phi}\boldsymbol{B}+\boldsymbol{E}\times \boldsymbol{A}$
. For a plasma with an Ohm’s law
 $\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}={\it\eta}\,\boldsymbol{j}$
,
$\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}={\it\eta}\,\boldsymbol{j}$
,
 $$\begin{eqnarray}\frac{\partial }{\partial t}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{Q}+2{\it\eta}(\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{B})=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial }{\partial t}(\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B})+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{Q}+2{\it\eta}(\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{B})=0.\end{eqnarray}$$
Neither
![]() $\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
nor
$\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}$
nor
![]() $\boldsymbol{Q}$
is gauge-invariant, but it is clear that
$\boldsymbol{Q}$
is gauge-invariant, but it is clear that
![]() $\boldsymbol{Q}$
must represent a flux of helicity. If we consider a small-amplitude
wave so that
$\boldsymbol{Q}$
must represent a flux of helicity. If we consider a small-amplitude
wave so that
 $\boldsymbol{B}=\boldsymbol{B}_{0}+\boldsymbol{b}\text{e}^{\text{i}{\it\omega}t}$
,
$\boldsymbol{B}=\boldsymbol{B}_{0}+\boldsymbol{b}\text{e}^{\text{i}{\it\omega}t}$
,
![]() $\boldsymbol{Q}$
becomes
$\boldsymbol{Q}$
becomes
 $$\begin{eqnarray}\boldsymbol{q}={\textstyle \frac{1}{2}}[{\it\phi}\boldsymbol{b}^{\ast }+(\boldsymbol{e}\times \boldsymbol{a}^{\ast })+\text{c.c.}],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}={\textstyle \frac{1}{2}}[{\it\phi}\boldsymbol{b}^{\ast }+(\boldsymbol{e}\times \boldsymbol{a}^{\ast })+\text{c.c.}],\end{eqnarray}$$
and we can therefore introduce a flux
 $$\begin{eqnarray}\boldsymbol{q}^{\prime }=\frac{\text{i}}{{\it\omega}}(\boldsymbol{e}\times \boldsymbol{e}^{\ast }),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}^{\prime }=\frac{\text{i}}{{\it\omega}}(\boldsymbol{e}\times \boldsymbol{e}^{\ast }),\end{eqnarray}$$
which has the same divergence as
![]() $\boldsymbol{q}$
but is manifestly gauge-invariant. This form also brings out the
connection between helicity and polarisation: a plane-polarised wave carries no
helicity. (Actually this is obvious, as a plane-polarised wave has complete mirror
symmetry whereas helicity is antisymmetric under reflection.)
$\boldsymbol{q}$
but is manifestly gauge-invariant. This form also brings out the
connection between helicity and polarisation: a plane-polarised wave carries no
helicity. (Actually this is obvious, as a plane-polarised wave has complete mirror
symmetry whereas helicity is antisymmetric under reflection.)
However, a circularly polarised wave, propagating parallel to
![]() $\boldsymbol{B}_{0}$
, with a vector potential given by the real part of
$\boldsymbol{B}_{0}$
, with a vector potential given by the real part of
 $$\begin{eqnarray}\boldsymbol{A}=(A,\text{i}A,0)\exp [\text{i}(kz-{\it\omega}t)],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=(A,\text{i}A,0)\exp [\text{i}(kz-{\it\omega}t)],\end{eqnarray}$$
does carry helicity in the form (13.7). (Here
![]() ${\it\omega}$
is real and
${\it\omega}$
is real and
![]() $k$
complex,
$k$
complex,
 $k=k_{0}({\it\omega})+\text{i}k_{1}({\it\omega})$
, as for waves generated by an antenna at
$k=k_{0}({\it\omega})+\text{i}k_{1}({\it\omega})$
, as for waves generated by an antenna at
![]() $z=0$
.)
$z=0$
.)
From (13.8)
 $$\begin{eqnarray}\boldsymbol{e}=(\text{i}{\it\omega}A,-{\it\omega}A,0)\exp [\text{i}(kz-{\it\omega}t)],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{e}=(\text{i}{\it\omega}A,-{\it\omega}A,0)\exp [\text{i}(kz-{\it\omega}t)],\end{eqnarray}$$
therefore
 $$\begin{eqnarray}\boldsymbol{q}^{\prime }=\boldsymbol{q}_{z}={\it\omega}|A|^{2}\text{e}^{-2k_{1}z}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}^{\prime }=\boldsymbol{q}_{z}={\it\omega}|A|^{2}\text{e}^{-2k_{1}z}.\end{eqnarray}$$
Define
 $|A|^{2}\text{e}^{-2k_{1}z}=A^{2}(z)$
, the square of the local wave amplitude, then
$|A|^{2}\text{e}^{-2k_{1}z}=A^{2}(z)$
, the square of the local wave amplitude, then
 $$\begin{eqnarray}\boldsymbol{q}_{z}={\it\omega}A^{2}(z)=v(k_{0}A^{2}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}_{z}={\it\omega}A^{2}(z)=v(k_{0}A^{2}),\end{eqnarray}$$
where
 $v={\it\omega}/k_{0}$
is the wave velocity. This can be interpreted as the wave carrying
helicity density
$v={\it\omega}/k_{0}$
is the wave velocity. This can be interpreted as the wave carrying
helicity density
![]() $k_{0}A^{2}$
. Finally, then,
$k_{0}A^{2}$
. Finally, then,
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}=-2{\it\omega}k_{1}A^{2}(z).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}=-2{\it\omega}k_{1}A^{2}(z).\end{eqnarray}$$
Now consider a specific plasma wave, an Alfvén wave in a resistive plasma, with
viscosity
![]() ${\it\nu}$
. The linearised wave equations are
${\it\nu}$
. The linearised wave equations are
 $$\begin{eqnarray}\displaystyle & \displaystyle -{\it\omega}\boldsymbol{b}=(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{v}+\text{i}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\boldsymbol{b}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\it\omega}\boldsymbol{b}=(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{v}+\text{i}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\boldsymbol{b}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle -{\it\omega}{\it\rho}\boldsymbol{v}=\frac{1}{{\it\mu}_{0}}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{b}+\text{i}{\it\rho}{\it\nu}k^{2}\boldsymbol{v}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -{\it\omega}{\it\rho}\boldsymbol{v}=\frac{1}{{\it\mu}_{0}}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{B})\boldsymbol{b}+\text{i}{\it\rho}{\it\nu}k^{2}\boldsymbol{v}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\left({\it\omega}+\text{i}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\right)({\it\omega}+\text{i}{\it\nu}k^{2})=k^{2}v_{A}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\left({\it\omega}+\text{i}\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}\right)({\it\omega}+\text{i}{\it\nu}k^{2})=k^{2}v_{A}^{2},\end{eqnarray}$$
where
![]() $v_{A}$
is the Alfvén speed (see (4.5)). When
$v_{A}$
is the Alfvén speed (see (4.5)). When
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\nu}$
are small,
${\it\nu}$
are small,
 $k_{0}\approx {\it\omega}/v_{A}$
and the wave damping is
$k_{0}\approx {\it\omega}/v_{A}$
and the wave damping is
 $k_{1}\approx ({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})k_{0}^{2}/2v_{A}$
. Therefore
$k_{1}\approx ({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})k_{0}^{2}/2v_{A}$
. Therefore
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}=-\left(\frac{{\it\eta}}{{\it\mu}_{0}}+{\it\nu}\right)k_{0}^{3}A^{2}(z).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}=-\left(\frac{{\it\eta}}{{\it\mu}_{0}}+{\it\nu}\right)k_{0}^{3}A^{2}(z).\end{eqnarray}$$
Thus it appears that we can indeed inject helicity from polarised
waves, and that the input is proportional to the total wave damping,
 $({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})$
.
$({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})$
.
As mentioned above, this form of helicity injection is conventionally interpreted as
current drive. The mean current induced by the wave fluctuations can be calculated
directly from Ohm’s law
 ${\it\eta}\langle \,j_{z}\rangle =\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
. If the wave equation (13.14) is used to express
${\it\eta}\langle \,j_{z}\rangle =\langle \boldsymbol{v}\times \boldsymbol{b}\rangle$
. If the wave equation (13.14) is used to express
![]() $\boldsymbol{v}$
in terms of
$\boldsymbol{v}$
in terms of
![]() $\boldsymbol{b}$
, then
$\boldsymbol{b}$
, then
 $$\begin{eqnarray}{\it\eta}\langle \,j_{z}\rangle =\frac{A^{2}(z)}{B_{0}}\left({\it\omega}k_{1}-\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}k_{0}\right)\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}\langle \,j_{z}\rangle =\frac{A^{2}(z)}{B_{0}}\left({\it\omega}k_{1}-\frac{{\it\eta}}{{\it\mu}_{0}}k^{2}k_{0}\right)\end{eqnarray}$$
and using
![]() $k_{1}$
as given above, the wave-driven current is
$k_{1}$
as given above, the wave-driven current is
 $$\begin{eqnarray}{\it\eta}\langle \,j_{z}\rangle =\frac{k_{0}^{3}A^{2}(z)}{2B_{0}}\left({\it\nu}-\frac{{\it\eta}}{{\it\mu}_{0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}\langle \,j_{z}\rangle =\frac{k_{0}^{3}A^{2}(z)}{2B_{0}}\left({\it\nu}-\frac{{\it\eta}}{{\it\mu}_{0}}\right).\end{eqnarray}$$
This is in agreement with the net helicity injection given by (13.4) in steady state,
 $$\begin{eqnarray}-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}-2{\it\eta}\langle \,\boldsymbol{j}_{{\it\omega}}\boldsymbol{\cdot }\boldsymbol{b}_{{\it\omega}}\rangle =[({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})-2{\it\eta}{\it\mu}_{0}^{-1}]k_{0}^{3}A^{2}(z)=({\it\nu}-{\it\eta}{\it\mu}_{0}^{-1})k_{0}^{3}A^{2}(z),\end{eqnarray}$$
$$\begin{eqnarray}-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{q}-2{\it\eta}\langle \,\boldsymbol{j}_{{\it\omega}}\boldsymbol{\cdot }\boldsymbol{b}_{{\it\omega}}\rangle =[({\it\eta}{\it\mu}_{0}^{-1}+{\it\nu})-2{\it\eta}{\it\mu}_{0}^{-1}]k_{0}^{3}A^{2}(z)=({\it\nu}-{\it\eta}{\it\mu}_{0}^{-1})k_{0}^{3}A^{2}(z),\end{eqnarray}$$
where
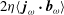 $2{\it\eta}\langle \,\boldsymbol{j}_{{\it\omega}}\boldsymbol{\cdot }\boldsymbol{b}_{{\it\omega}}\rangle$
is the decay of helicity associated with the wave fluctuations
(13.8) themselves. Note the
remarkable fact that, if resistivity were the only damping, the loss of helicity
through the wave fluctuations would be exactly twice the input from the wave.
$2{\it\eta}\langle \,\boldsymbol{j}_{{\it\omega}}\boldsymbol{\cdot }\boldsymbol{b}_{{\it\omega}}\rangle$
is the decay of helicity associated with the wave fluctuations
(13.8) themselves. Note the
remarkable fact that, if resistivity were the only damping, the loss of helicity
through the wave fluctuations would be exactly twice the input from the wave.
14. General theory of relaxed toroidal states
It is interesting to cast the theory of relaxed states in a general form that illustrates the connection between different types of relaxed state (Jensen & Chu Reference Jensen and Chu1984; Taylor Reference Taylor1986). (Even though it is not a convenient way to study specific examples.)
In a general toroidal system, the relaxed state is the lowest-energy, that is, smallest-
![]() ${\it\mu}$
, solution of
${\it\mu}$
, solution of
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})={\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{A})={\it\mu}\boldsymbol{{\rm\nabla}}\times \boldsymbol{A},\end{eqnarray}$$
with
 $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}=0$
on the boundary and
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}=0$
on the boundary and
![]() $\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}$
,
$\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{l}$
,
 $\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}\equiv {\it\Psi}$
and
$\oint \boldsymbol{A}\boldsymbol{\cdot }\text{d}\boldsymbol{s}\equiv {\it\Psi}$
and
 $\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}\equiv K$
specified. (The use of
$\int \boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}\;\text{d}{\it\tau}\equiv K$
specified. (The use of
![]() $\boldsymbol{A}$
instead of
$\boldsymbol{A}$
instead of
![]() $\boldsymbol{B}$
allows all constraints to be set as boundary conditions.)
$\boldsymbol{B}$
allows all constraints to be set as boundary conditions.)
To describe the possible relaxed states, we must also introduce the eigenfunctions defined by
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i})={\it\lambda}_{i}\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times (\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i})={\it\lambda}_{i}\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i},\end{eqnarray}$$
with boundary condition
![]() $\boldsymbol{a}_{i}=0$
. Note that the eigenfunctions carry no toroidal flux.
$\boldsymbol{a}_{i}=0$
. Note that the eigenfunctions carry no toroidal flux.
As we found explicitly in the case of the circular cylinder, the relaxed state is one of two possibilities:
-
(i) a primitive solution of (14.1) in which
 ${\it\mu}$
is determined by
${\it\mu}$
is determined by
 $K/{\it\Psi}^{2}$
;
$K/{\it\Psi}^{2}$
; -
(ii) a mixed solution, that is, a superposition of a primitive solution and an eigenfunction, in which case
 ${\it\mu}$
is determined as the smallest eigenvalue and
${\it\mu}$
is determined as the smallest eigenvalue and
 $K/{\it\Psi}^{2}$
determines the relative amplitudes of the eigenfunction and
primitive components.
$K/{\it\Psi}^{2}$
determines the relative amplitudes of the eigenfunction and
primitive components.
To see what differences, if any, might arise in a general toroidal system, we assume
that the
![]() $\boldsymbol{a}_{i}$
are a sufficiently complete set and write the solution as
$\boldsymbol{a}_{i}$
are a sufficiently complete set and write the solution as
 $$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\sum {\it\alpha}_{i}\,\boldsymbol{a}_{i},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\sum {\it\alpha}_{i}\,\boldsymbol{a}_{i},\end{eqnarray}$$
where
![]() $\boldsymbol{A}_{0}$
is the vector potential for a vacuum field that satisfies the same
boundary conditions as the actual problem. The eigenfunctions are orthogonal, where the
following integrals are taken over the system volume:
$\boldsymbol{A}_{0}$
is the vector potential for a vacuum field that satisfies the same
boundary conditions as the actual problem. The eigenfunctions are orthogonal, where the
following integrals are taken over the system volume:
 $$\begin{eqnarray}({\it\lambda}_{i}-{\it\lambda}_{j})\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{j}\;\text{d}{\it\tau}=0\end{eqnarray}$$
$$\begin{eqnarray}({\it\lambda}_{i}-{\it\lambda}_{j})\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{j}\;\text{d}{\it\tau}=0\end{eqnarray}$$
and
 $$\begin{eqnarray}{\it\lambda}_{i}\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i}\;\text{d}{\it\tau}=\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i})^{2}\,\text{d}{\it\tau}>0,\end{eqnarray}$$
$$\begin{eqnarray}{\it\lambda}_{i}\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i}\;\text{d}{\it\tau}=\int (\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i})^{2}\,\text{d}{\it\tau}>0,\end{eqnarray}$$
so they can be normalised such that
 $$\begin{eqnarray}\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{j}\;\text{d}{\it\tau}=\int \boldsymbol{a}_{j}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i}\;\text{d}{\it\tau}=\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}{\it\delta}_{ij}.\end{eqnarray}$$
$$\begin{eqnarray}\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{j}\;\text{d}{\it\tau}=\int \boldsymbol{a}_{j}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{a}_{i}\;\text{d}{\it\tau}=\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}{\it\delta}_{ij}.\end{eqnarray}$$
Substituting (14.3)
into the relaxed-state equation (14.1), and using the orthogonality of the eigenfunctions, we can find the
![]() ${\it\alpha}_{i}$
– provided
${\it\alpha}_{i}$
– provided
![]() ${\it\mu}$
is not an eigenvalue. Then
${\it\mu}$
is not an eigenvalue. Then
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}T_{i}\,\boldsymbol{a}_{i}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}T_{i}\,\boldsymbol{a}_{i}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle T_{i}\equiv \int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0}\;\text{d}{\it\tau} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{i}\equiv \int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0}\;\text{d}{\it\tau} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\frac{K}{{\it\Psi}^{2}}=\frac{1}{{\it\Psi}^{2}}\left\{\int (\boldsymbol{A}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0})\,\text{d}{\it\tau}+\mathop{\sum }_{i}T_{i}^{2}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}\left(\frac{{\it\lambda}_{i}^{2}}{({\it\lambda}_{i}-{\it\mu})^{2}}-1\right)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{K}{{\it\Psi}^{2}}=\frac{1}{{\it\Psi}^{2}}\left\{\int (\boldsymbol{A}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0})\,\text{d}{\it\tau}+\mathop{\sum }_{i}T_{i}^{2}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}\left(\frac{{\it\lambda}_{i}^{2}}{({\it\lambda}_{i}-{\it\mu})^{2}}-1\right)\right\}.\end{eqnarray}$$
This defines
![]() ${\it\mu}$
as
${\it\mu}$
as
 ${\it\mu}=f(K/{\it\Psi}^{2})$
. We are interested only in the smallest
${\it\mu}=f(K/{\it\Psi}^{2})$
. We are interested only in the smallest
![]() ${\it\mu}$
, which must lie below
${\it\mu}$
, which must lie below
![]() ${\it\lambda}_{0}$
because
${\it\lambda}_{0}$
because
 $K/{\it\Psi}^{2}\rightarrow \infty$
as
$K/{\it\Psi}^{2}\rightarrow \infty$
as
![]() ${\it\mu}\rightarrow {\it\lambda}_{0}$
.
${\it\mu}\rightarrow {\it\lambda}_{0}$
.
However, many eigenfunctions may be decoupled from the vacuum field, that is
 $$\begin{eqnarray}T_{i}=\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0}\;\text{d}{\it\tau}=0.\end{eqnarray}$$
$$\begin{eqnarray}T_{i}=\int \boldsymbol{a}_{i}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{A}_{0}\;\text{d}{\it\tau}=0.\end{eqnarray}$$
For example, in an axisymmetric (but not necessarily circular
cross-section) system, all the non-axisymmetric eigenfunctions
 ${\sim}\exp (\text{i}n{\it\phi})$
are decoupled from the axisymmetric vacuum field.
Some axisymmetric eigenfunctions may also be decoupled, e.g. by the (anti)symmetry about
the equatorial plane, as in the multipinch. To remind us of this we write
${\sim}\exp (\text{i}n{\it\phi})$
are decoupled from the axisymmetric vacuum field.
Some axisymmetric eigenfunctions may also be decoupled, e.g. by the (anti)symmetry about
the equatorial plane, as in the multipinch. To remind us of this we write
 $$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i},\end{eqnarray}$$
where
![]() $\sum _{i}^{\prime }$
denotes the sum only over coupled eigenfunctions.
$\sum _{i}^{\prime }$
denotes the sum only over coupled eigenfunctions.
If the lowest eigenfunction (that with the smallest
![]() ${\it\lambda}_{0}$
) is not decoupled (
${\it\lambda}_{0}$
) is not decoupled (
![]() $T_{0}\neq 0$
), the relaxed state (14.7) exhibits a ‘soft’ form of current saturation in which the toroidal
current
$T_{0}\neq 0$
), the relaxed state (14.7) exhibits a ‘soft’ form of current saturation in which the toroidal
current
![]() $I\rightarrow I_{sat}$
as
$I\rightarrow I_{sat}$
as
 $K/{\it\Psi}^{2}\rightarrow \infty$
(see (14.9) and the
dashed line in figure 45).
$K/{\it\Psi}^{2}\rightarrow \infty$
(see (14.9) and the
dashed line in figure 45).

Figure 45. Current saturation in general relaxed states: soft (dashed) and hard (solid).
Lowest eigenvalue is
![]() ${\it\mu}_{0}$
.
${\it\mu}_{0}$
.
If the lowest eigenfunction
![]() $\boldsymbol{a}_{0}$
is decoupled, then when
$\boldsymbol{a}_{0}$
is decoupled, then when
![]() ${\it\mu}={\it\lambda}_{0}$
we can add a term
${\it\mu}={\it\lambda}_{0}$
we can add a term
![]() ${\it\beta}\boldsymbol{a}_{0}$
to the sum (14.11)
(which otherwise does not contain
${\it\beta}\boldsymbol{a}_{0}$
to the sum (14.11)
(which otherwise does not contain
![]() $\boldsymbol{a}_{0}$
) to create a state in which
$\boldsymbol{a}_{0}$
) to create a state in which
![]() ${\it\beta}$
is determined by
${\it\beta}$
is determined by
![]() $K/{\it\Psi}^{2}$
. This state exhibits a ‘hard’ saturation in which the toroidal current
abruptly stops increasing when
$K/{\it\Psi}^{2}$
. This state exhibits a ‘hard’ saturation in which the toroidal current
abruptly stops increasing when
![]() $K/{\it\Psi}^{2}$
reaches a finite critical value (solid line in figure 45).
$K/{\it\Psi}^{2}$
reaches a finite critical value (solid line in figure 45).
At this point one should ask the following questions. What if, as is always the case in
the real world, there are small field errors in a supposedly axisymmetric system, which
couple the supposedly decoupled
![]() $\boldsymbol{a}_{0}$
to the vacuum field? Does one then get a primitive state with soft
saturation or a mixed state with hard saturation?
$\boldsymbol{a}_{0}$
to the vacuum field? Does one then get a primitive state with soft
saturation or a mixed state with hard saturation?
In fact, there is no anomaly. If small field errors are incorporated, we have
 $$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i}+\frac{{\it\mu}}{({\it\lambda}_{0}-{\it\mu})}\frac{{\it\lambda}_{0}}{|{\it\lambda}_{0}|}\tilde{T}_{0}\,\boldsymbol{a}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i}+\frac{{\it\mu}}{({\it\lambda}_{0}-{\it\mu})}\frac{{\it\lambda}_{0}}{|{\it\lambda}_{0}|}\tilde{T}_{0}\,\boldsymbol{a}_{0},\end{eqnarray}$$
where
![]() $\tilde{T}_{0}$
is the coupling to the error field, and if the error field is ignored
we have
$\tilde{T}_{0}$
is the coupling to the error field, and if the error field is ignored
we have
 $$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i}+{\it\beta}\boldsymbol{a}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=\boldsymbol{A}_{0}+\mathop{\sum }_{i}^{\prime }\frac{{\it\mu}}{({\it\lambda}_{i}-{\it\mu})}\frac{{\it\lambda}_{i}}{|{\it\lambda}_{i}|}T_{i}\,\boldsymbol{a}_{i}+{\it\beta}\boldsymbol{a}_{0}.\end{eqnarray}$$
Taking the view that we should include error fields, if we let these
decrease so that
![]() $\tilde{T}_{0}\rightarrow 0$
, then we find that (for fixed
$\tilde{T}_{0}\rightarrow 0$
, then we find that (for fixed
![]() $K/{\it\Psi}^{2}$
)
$K/{\it\Psi}^{2}$
)
![]() ${\it\mu}\rightarrow {\it\lambda}_{0}$
and the limit
${\it\mu}\rightarrow {\it\lambda}_{0}$
and the limit
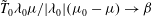 $\tilde{T}_{0}{\it\lambda}_{0}{\it\mu}/|{\it\lambda}_{0}|({\it\mu}_{0}-{\it\mu})\rightarrow {\it\beta}$
, so we have the same result as when field errors are ignored.
Consequently, the soft saturation with field errors simply goes over to the hard
saturation as field errors diminish (see figure 45).
$\tilde{T}_{0}{\it\lambda}_{0}{\it\mu}/|{\it\lambda}_{0}|({\it\mu}_{0}-{\it\mu})\rightarrow {\it\beta}$
, so we have the same result as when field errors are ignored.
Consequently, the soft saturation with field errors simply goes over to the hard
saturation as field errors diminish (see figure 45).
15. Conclusion
The theory of relaxation has been remarkably successful in accounting for, and predicting, the behaviour of turbulent plasmas in many different circumstances. Even more remarkable is that it does this from ‘first principles’ – there are no fitted or arbitrary parameters in the calculation of relaxed states.
It is therefore important to be clear about the scope and limits of the theory. Some significant points are:
-
(i) Relaxation is a theory of turbulent plasma. It is turbulence, allied to a small resistivity, that enables the plasma to reach the relaxed state. A plasma, or a simulation, that is at all times stable or quiescent will not relax.
-
(ii) Because relaxation depends on turbulence, there is always some uncertainty whether relaxation will be complete. This is particularly relevant in tokamak experiments where there is a strong stabilising vacuum magnetic field, unlike the experiments we have discussed in which the magnetic field is largely generated by currents in the plasma. (Currents in the plasma are free to move; those in massive external metal coils are not supposed to!) Also, tokamaks are carefully designed and operated to maintain stability as far as possible. Consequently it appears that relaxation in tokamaks is only partial and limited, as in sawteeth and disruptions – and even these are avoided as much as possible.
-
(iii) Relaxation theory is concerned with actual plasma motions. Despite its mathematical similarity, it should not be confused with purely mathematical minimisation principles involving virtual displacements, such as Hamilton’s principle. Nor should one arbitrarily add extra conserved mathematical quantities unless there is a physical reason to do so. The cornerstone of the theory is that turbulence plus resistivity introduces localised reconnection that scarcely changes total helicity, but has a global effect on plasma behaviour.
-
(iv) Relaxation theory says nothing about exactly how the plasma gets to the relaxed state. (This is both its great strength and its weakness.) It describes only the state the plasma eventually (though very rapidly compared to resistive processes) reaches. In this regard it is similar to a statistical derivation of thermal distributions, which also does not describe in detail how this distribution is reached.
-
(v) You will have noticed that we have said nothing about plasma pressure and that all relaxed states are force-free, stable, equilibria. This is because, if lines of force are free to break and reconnect, we must expect that pressure will be equalised by flow along the field during this reconnection. One might suggest that this equalisation would be slower than reconnection, but to describe it would need a full theory of plasma turbulence capable of calculating the development from initial to final state. Not only do we lack such a theory, but it would not be in any way universal – which was the original requirement of a theory to explain the quiescent states.
-
(vi) In the historical development of confinement systems a distinction was initially drawn between (1) those like mirrors and stellarators, in which one could envisage setting up an unquestionably stable vacuum field and adding plasma as a perturbation, and (2) those like toroidal pinches, in which the plasma itself produced much of the confining field and which therefore lacked the obvious stability of a vacuum field. One might claim that the discovery of relaxed states somewhat reduced this distinction, with the relaxed state playing the role of the vacuum field.
Part III
16. Adiabatic traps and mirror machines
So far, we have concentrated on toroidal confinement systems and the fluid model. Now we turn to a different confinement system – the adiabatic trap – and the guiding centre model.
In an adiabatic trap, the magnetic field lines are not confined to the
system. (Recall that this is only possible in a torus.) Instead, plasma loss along the
field lines is inhibited by the ‘magnetic mirror’ effect. This depends on the existence
of an ‘adiabatic invariant’ for each particle – its magnetic moment
 ${\it\mu}=mv_{\bot }^{2}/2B$
.
${\it\mu}=mv_{\bot }^{2}/2B$
.
The invariance of
![]() ${\it\mu}$
, together with the fact that the total energy,
${\it\mu}$
, together with the fact that the total energy,
![]() $E$
, of a particle is constant in a static field, means that
$E$
, of a particle is constant in a static field, means that
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}mv_{\Vert }^{2}=E-{\it\mu}B,\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}mv_{\Vert }^{2}=E-{\it\mu}B,\end{eqnarray}$$
so that
![]() ${\it\mu}B$
acts as a potential for the parallel motion. Particles in a field
${\it\mu}B$
acts as a potential for the parallel motion. Particles in a field
![]() $B_{0}$
are therefore ‘reflected’ by a stronger field
$B_{0}$
are therefore ‘reflected’ by a stronger field
![]() $B_{m}$
if their velocity lies outside the ‘loss cone’
$B_{m}$
if their velocity lies outside the ‘loss cone’
 $$\begin{eqnarray}\left(\frac{v_{\bot }}{v}\right)<\left(\frac{B_{0}}{B_{m}}\right)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{v_{\bot }}{v}\right)<\left(\frac{B_{0}}{B_{m}}\right)^{1/2}.\end{eqnarray}$$
A typical mirror machine based on this effect is shown in figure 46.

Figure 46. Mirror machine (from Taylor Reference Taylor1968).
Note that the existence of a loss cone in velocity space means that the plasma pressure in an adiabatic trap is always anisotropic. This is an important distinction between adiabatic traps and toroidal systems – which usually have near-isotropic pressure. It also means that scattering into the loss cone inevitably leads to loss of plasma in mirror machines.
16.1. Digression on adiabatic invariants
Adiabatic invariants are an interesting feature of classical mechanics and were important in the ‘old’ quantum theory – where they were the classical variables that became ‘quantised’, i.e. restricted to discrete values.
An adiabatic invariant arises when the motion of a classical particle, with
Hamiltonian
 $H(p,q,a_{i})$
, is periodic – as it must be in one dimension if it is bounded
(Goldstein Reference Goldstein1957). Then if the parameters
$H(p,q,a_{i})$
, is periodic – as it must be in one dimension if it is bounded
(Goldstein Reference Goldstein1957). Then if the parameters
![]() $a_{i}$
are changed slowly compared to the period of oscillation, the
resulting quasi-periodic motion possesses an invariant
$a_{i}$
are changed slowly compared to the period of oscillation, the
resulting quasi-periodic motion possesses an invariant
 $$\begin{eqnarray}I=\oint p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}I=\oint p\,\text{d}q,\end{eqnarray}$$
which acts as a ‘constant of motion’ in a sense that will be explained shortly.
The classic example of such an invariant is associated with the motion of a pendulum
whose length is changed slowly. In this case the invariant is the energy
![]() $E(t)$
divided by the frequency
$E(t)$
divided by the frequency
![]() ${\it\omega}(t)$
of the pendulum,
${\it\omega}(t)$
of the pendulum,
i.e. as the length of the pendulum is altered, the change in its
energy is proportional to the change in its frequency. (This is a hint that there
might be a connection with quantum states,
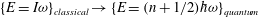 $\{E=I{\it\omega}\}_{classical}\rightarrow \{E=(n+1/2)\hbar{\it\omega}\}_{quantum}$
.)
$\{E=I{\it\omega}\}_{classical}\rightarrow \{E=(n+1/2)\hbar{\it\omega}\}_{quantum}$
.)
It is important to note that the distinguishing feature of an invariant is not, as is sometimes stated, that it varies slowly – it is that changes in the invariant remain small for an indefinite time.
Now let us look at what we mean when we say that the invariant acts as a constant of motion.
The Hamiltonian for a harmonic oscillator with unit mass is
 $$\begin{eqnarray}H=\frac{p^{2}}{2}+{\it\omega}^{2}(t)\frac{q^{2}}{2}\equiv E\end{eqnarray}$$
$$\begin{eqnarray}H=\frac{p^{2}}{2}+{\it\omega}^{2}(t)\frac{q^{2}}{2}\equiv E\end{eqnarray}$$
and, when
![]() ${\it\omega}$
is constant,
${\it\omega}$
is constant,
 $$\begin{eqnarray}p=a\cos ({\it\omega}t+{\it\lambda}),\quad q=a{\it\omega}\sin ({\it\omega}t+{\it\lambda}).\end{eqnarray}$$
$$\begin{eqnarray}p=a\cos ({\it\omega}t+{\it\lambda}),\quad q=a{\it\omega}\sin ({\it\omega}t+{\it\lambda}).\end{eqnarray}$$
To find the invariant when
![]() ${\it\omega}(t)$
varies slowly, we first transform to new variables
${\it\omega}(t)$
varies slowly, we first transform to new variables
![]() $P$
and
$P$
and
![]() $Q$
, such that
$Q$
, such that
 $$\begin{eqnarray}\displaystyle & p\rightarrow (2{\it\omega}P)^{1/2}\cos Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & p\rightarrow (2{\it\omega}P)^{1/2}\cos Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle q\rightarrow \left(\frac{2P}{{\it\omega}}\right)^{1/2}\sin Q. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle q\rightarrow \left(\frac{2P}{{\it\omega}}\right)^{1/2}\sin Q. & \displaystyle\end{eqnarray}$$
 $F(q,Q)=({\it\omega}/2)q^{2}\cot Q$
; see Goldstein (Reference Goldstein1957).) Then
the new Hamiltonian is
$F(q,Q)=({\it\omega}/2)q^{2}\cot Q$
; see Goldstein (Reference Goldstein1957).) Then
the new Hamiltonian is  $$\begin{eqnarray}H={\it\omega}(t)P+\frac{\dot{{\it\omega}}}{2{\it\omega}}P\sin 2Q,\end{eqnarray}$$
$$\begin{eqnarray}H={\it\omega}(t)P+\frac{\dot{{\it\omega}}}{2{\it\omega}}P\sin 2Q,\end{eqnarray}$$
and the equations of motion become
 $$\begin{eqnarray}\displaystyle & \displaystyle {\dot{P}}=-\frac{\dot{{\it\omega}}}{{\it\omega}}P\cos 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{P}}=-\frac{\dot{{\it\omega}}}{{\it\omega}}P\cos 2Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \dot{Q}={\it\omega}+\frac{\dot{{\it\omega}}}{2{\it\omega}}\sin 2Q. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{Q}={\it\omega}+\frac{\dot{{\it\omega}}}{2{\it\omega}}\sin 2Q. & \displaystyle\end{eqnarray}$$
We now introduce a slow time dependence of the oscillation frequency, via the small
parameter
![]() ${\it\epsilon}$
, by writing
${\it\epsilon}$
, by writing
 ${\it\omega}={\it\omega}({\it\epsilon}t)$
, and look for an invariant as a power series in
${\it\omega}={\it\omega}({\it\epsilon}t)$
, and look for an invariant as a power series in
![]() ${\it\epsilon}$
:
${\it\epsilon}$
:
 $$\begin{eqnarray}\text{constant}=J(P,Q,{\it\epsilon}t)=J_{0}(P,Q)+{\it\epsilon}J_{1}(P,Q,{\it\epsilon}t)+{\it\epsilon}^{2}J_{2}(P,Q,{\it\epsilon}t)+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\text{constant}=J(P,Q,{\it\epsilon}t)=J_{0}(P,Q)+{\it\epsilon}J_{1}(P,Q,{\it\epsilon}t)+{\it\epsilon}^{2}J_{2}(P,Q,{\it\epsilon}t)+\cdots \,.\end{eqnarray}$$
Then requiring
 $$\begin{eqnarray}\frac{\text{d}J}{\text{d}t}={\it\epsilon}\frac{\partial J}{\partial t}+\frac{\partial J}{\partial P}{\dot{P}}+\frac{\partial J}{\partial Q}\dot{Q}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}J}{\text{d}t}={\it\epsilon}\frac{\partial J}{\partial t}+\frac{\partial J}{\partial P}{\dot{P}}+\frac{\partial J}{\partial Q}\dot{Q}=0,\end{eqnarray}$$
and using (16.11), we obtain, order by order, the recurrence relation
 $$\begin{eqnarray}{\it\omega}\frac{\partial J_{n}}{\partial Q}=-\frac{\partial J_{n-1}}{\partial t}-\frac{\dot{{\it\omega}}}{{\it\omega}}\left[\frac{1}{2}\sin 2Q\,\frac{\partial J_{n-1}}{\partial Q}-P\cos 2Q\,\frac{\partial J_{n-1}}{\partial P}\right].\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}\frac{\partial J_{n}}{\partial Q}=-\frac{\partial J_{n-1}}{\partial t}-\frac{\dot{{\it\omega}}}{{\it\omega}}\left[\frac{1}{2}\sin 2Q\,\frac{\partial J_{n-1}}{\partial Q}-P\cos 2Q\,\frac{\partial J_{n-1}}{\partial P}\right].\end{eqnarray}$$
This allows us to generate the invariant term by term. The first term
![]() $J_{0}$
must be a function of
$J_{0}$
must be a function of
![]() $P$
only, and if we choose
$P$
only, and if we choose
![]() $J_{0}\equiv P$
then, using (16.8), we can confirm that this is indeed the integral
$J_{0}\equiv P$
then, using (16.8), we can confirm that this is indeed the integral
![]() $I$
introduced earlier (equation (16.3)),
$I$
introduced earlier (equation (16.3)),
 $$\begin{eqnarray}I=\oint p\,\text{d}q=\oint \sqrt{2{\it\omega}P}\cos Q\;\sqrt{\frac{2P}{{\it\omega}}}\cos Q\;\text{d}Q\equiv P.\end{eqnarray}$$
$$\begin{eqnarray}I=\oint p\,\text{d}q=\oint \sqrt{2{\it\omega}P}\cos Q\;\sqrt{\frac{2P}{{\it\omega}}}\cos Q\;\text{d}Q\equiv P.\end{eqnarray}$$
The next few terms in the series are
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{1}=\frac{1}{2}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)P\sin 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{1}=\frac{1}{2}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)P\sin 2Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{2}=\frac{1}{8}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)^{2}P+\frac{1}{4{\it\omega}}\frac{\partial }{\partial t}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)P\cos 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{2}=\frac{1}{8}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)^{2}P+\frac{1}{4{\it\omega}}\frac{\partial }{\partial t}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)P\cos 2Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{3}=\left[\frac{1}{16}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)^{3}-\frac{1}{8}\left(\frac{1}{{\it\omega}}\frac{\partial }{\partial t}\right)^{2}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)\right]P\sin 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{3}=\left[\frac{1}{16}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)^{3}-\frac{1}{8}\left(\frac{1}{{\it\omega}}\frac{\partial }{\partial t}\right)^{2}\left(\frac{\dot{{\it\omega}}}{{\it\omega}^{2}}\right)\right]P\sin 2Q, & \displaystyle\end{eqnarray}$$
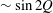 ${\sim}\sin 2Q$
and even-numbered terms
${\sim}\sin 2Q$
and even-numbered terms
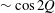 ${\sim}\cos 2Q$
plus a quantity independent of
${\sim}\cos 2Q$
plus a quantity independent of
So, now we see that
 $I=P=\oint p\,\text{d}q$
is actually only the first term of an expansion of the invariant
$I=P=\oint p\,\text{d}q$
is actually only the first term of an expansion of the invariant
![]() $J$
in powers of
$J$
in powers of
![]() ${\it\epsilon}$
. However, the important point is that all the higher-order terms in
this series are small and vanish when
${\it\epsilon}$
. However, the important point is that all the higher-order terms in
this series are small and vanish when
![]() ${\it\omega}(t)$
is constant. So if
${\it\omega}(t)$
is constant. So if
![]() ${\it\omega}(t)$
starts from a steady value at
${\it\omega}(t)$
starts from a steady value at
 $t\rightarrow -\infty$
, then changes slowly before eventually returning to a steady value
at
$t\rightarrow -\infty$
, then changes slowly before eventually returning to a steady value
at
 $t\rightarrow +\infty$
, the initial and final values of
$t\rightarrow +\infty$
, the initial and final values of
 $I=\oint p\,\text{d}q$
should be the same. Hence, in this sense the series (16.12) is an exact constant of
motion.
$I=\oint p\,\text{d}q$
should be the same. Hence, in this sense the series (16.12) is an exact constant of
motion.
Perhaps surprisingly, this is not what actually happens. In fact, the initial and
final values of
![]() $I$
differ by a small quantity that does not appear in the power series
– because it cannot be expanded in
$I$
differ by a small quantity that does not appear in the power series
– because it cannot be expanded in
![]() ${\it\epsilon}$
. This difference, often called the ‘non-adiabatic change’, is of
the form (Hastie et al.
Reference Hastie, Hobbs and Taylor1969)
${\it\epsilon}$
. This difference, often called the ‘non-adiabatic change’, is of
the form (Hastie et al.
Reference Hastie, Hobbs and Taylor1969)
 $$\begin{eqnarray}\frac{{\rm\Delta}I_{na}}{I}\sim A\,\text{e}^{-{\it\alpha}/{\it\epsilon}}\cos {\it\phi},\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\rm\Delta}I_{na}}{I}\sim A\,\text{e}^{-{\it\alpha}/{\it\epsilon}}\cos {\it\phi},\end{eqnarray}$$
where
![]() $A$
and
$A$
and
![]() ${\it\alpha}$
are constants as
${\it\alpha}$
are constants as
![]() ${\it\epsilon}\rightarrow 0$
and
${\it\epsilon}\rightarrow 0$
and
![]() ${\it\phi}$
is the phase of the oscillation at some reference point (usually
the point at which the phase is changing most slowly). This situation leads to the
statement that an adiabatic invariant is ‘constant to all orders – but not a
constant’.
${\it\phi}$
is the phase of the oscillation at some reference point (usually
the point at which the phase is changing most slowly). This situation leads to the
statement that an adiabatic invariant is ‘constant to all orders – but not a
constant’.
(A hint that there must be a non-adiabatic contribution comes from the correspondence between a classical invariant and quantum states mentioned earlier. If the frequency of a quantum oscillator is altered slowly and then returned to its original value, the oscillator would not return to its original state. Instead, it would have an exponentially small probability of being in ‘excited’ states. The classical limit of this is the non-adiabatic change.)
A rigorous calculation of the non-adiabatic change (which, of course, cannot be
obtained from an expansion or iteration in
![]() ${\it\epsilon}$
) is very lengthy, but a strong indication of its exponential form
can be given rather easily. If we return to (16.11),
${\it\epsilon}$
) is very lengthy, but a strong indication of its exponential form
can be given rather easily. If we return to (16.11),
 $$\begin{eqnarray}\displaystyle & \displaystyle {\dot{P}}=-\frac{\dot{{\it\omega}}}{{\it\omega}}P\cos 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{P}}=-\frac{\dot{{\it\omega}}}{{\it\omega}}P\cos 2Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \dot{Q}={\it\omega}+\frac{\dot{{\it\omega}}}{2{\it\omega}}\sin 2Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{Q}={\it\omega}+\frac{\dot{{\it\omega}}}{2{\it\omega}}\sin 2Q, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}Q\sim \int ^{t}{\it\omega}({\it\epsilon}t^{\prime })\,\text{d}t^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}Q\sim \int ^{t}{\it\omega}({\it\epsilon}t^{\prime })\,\text{d}t^{\prime },\end{eqnarray}$$
we have
 $$\begin{eqnarray}\frac{{\rm\Delta}P}{P}\sim \int _{-\infty }^{\infty }\frac{\dot{{\it\omega}}({\it\tau})}{{\it\omega}({\it\tau})}\exp \left[-\frac{\text{i}}{{\it\epsilon}}\int ^{{\it\tau}}{\it\omega}({\it\tau}^{\prime })\,\text{d}{\it\tau}^{\prime }\right]\text{d}{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\rm\Delta}P}{P}\sim \int _{-\infty }^{\infty }\frac{\dot{{\it\omega}}({\it\tau})}{{\it\omega}({\it\tau})}\exp \left[-\frac{\text{i}}{{\it\epsilon}}\int ^{{\it\tau}}{\it\omega}({\it\tau}^{\prime })\,\text{d}{\it\tau}^{\prime }\right]\text{d}{\it\tau}.\end{eqnarray}$$
If
![]() ${\it\omega}({\it\tau})$
is analytic, this can be evaluated by contour integration, with the
result
${\it\omega}({\it\tau})$
is analytic, this can be evaluated by contour integration, with the
result
 $$\begin{eqnarray}\frac{|{\rm\Delta}P|}{P}=A\exp \left(-\frac{{\it\alpha}}{{\it\epsilon}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\frac{|{\rm\Delta}P|}{P}=A\exp \left(-\frac{{\it\alpha}}{{\it\epsilon}}\right),\end{eqnarray}$$
where
![]() $A$
and
$A$
and
![]() ${\it\alpha}$
are related to the order and position of the (complex) zero of
${\it\alpha}$
are related to the order and position of the (complex) zero of
![]() ${\it\omega}({\it\tau})$
closest to the real axis.
${\it\omega}({\it\tau})$
closest to the real axis.
16.2. Invariants and particle orbits
The motion of a charged particle in a time-dependent uniform field
![]() $B(t)$
is exactly equivalent to a harmonic oscillator. To see this, it is
convenient to take the vector potential
$B(t)$
is exactly equivalent to a harmonic oscillator. To see this, it is
convenient to take the vector potential
 $$\begin{eqnarray}\boldsymbol{A}(t)=(-yB(t),xB(t),0).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}(t)=(-yB(t),xB(t),0).\end{eqnarray}$$
Then the Hamiltonian is
 $$\begin{eqnarray}H={\textstyle \frac{1}{2}}(p_{x}+yB(t))^{2}+{\textstyle \frac{1}{2}}(p_{y}-xB(t))^{2},\end{eqnarray}$$
$$\begin{eqnarray}H={\textstyle \frac{1}{2}}(p_{x}+yB(t))^{2}+{\textstyle \frac{1}{2}}(p_{y}-xB(t))^{2},\end{eqnarray}$$
from which we get the equations of motion in the form
 $$\begin{eqnarray}\ddot{z}+\text{i}B{\dot{z}}+\text{i}\frac{{\dot{B}}}{2}z=0,\end{eqnarray}$$
$$\begin{eqnarray}\ddot{z}+\text{i}B{\dot{z}}+\text{i}\frac{{\dot{B}}}{2}z=0,\end{eqnarray}$$
where
 $z=x+\text{i}y$
. (The term in
$z=x+\text{i}y$
. (The term in
![]() ${\dot{z}}$
is the Lorentz,
${\dot{z}}$
is the Lorentz,
![]() $\boldsymbol{v}\times \boldsymbol{B}$
, term and that in
$\boldsymbol{v}\times \boldsymbol{B}$
, term and that in
![]() ${\dot{B}}$
is due to the induced electric field.) Writing
${\dot{B}}$
is due to the induced electric field.) Writing
 $$\begin{eqnarray}z=q\exp \left(-\text{i}\int ^{t}\frac{B({\it\tau})}{2}\,\text{d}{\it\tau}\right)\end{eqnarray}$$
$$\begin{eqnarray}z=q\exp \left(-\text{i}\int ^{t}\frac{B({\it\tau})}{2}\,\text{d}{\it\tau}\right)\end{eqnarray}$$
reduces (16.27) to the oscillator equation
 $$\begin{eqnarray}\ddot{q}+{\textstyle \frac{1}{4}}B^{2}(t)q=0.\end{eqnarray}$$
$$\begin{eqnarray}\ddot{q}+{\textstyle \frac{1}{4}}B^{2}(t)q=0.\end{eqnarray}$$
So we can carry over the results we obtained for the oscillator to
the charged particle in a uniform field: then the lowest-order invariant is the
magnetic moment
![]() $mv_{\bot }^{2}/B$
as we anticipated.
$mv_{\bot }^{2}/B$
as we anticipated.
Unfortunately, we are interested in the motion of a particle in a static, non-uniform
field, rather than in a time-dependent, uniform one. This is a far more complex
problem that cannot be reduced to harmonic motion. Nevertheless, the qualitative
features of the adiabatic invariant are similar to those for the harmonic oscillator.
Thus there is a power-series expansion for the invariant, now in powers of the ratio
of Larmor radius to the scale of the variation in magnetic field. Since this is
proportional to
![]() $m/e$
, we can formally use
$m/e$
, we can formally use
 ${\it\lambda}\equiv m/e$
as an expansion parameter; then the first term is
${\it\lambda}\equiv m/e$
as an expansion parameter; then the first term is
![]() $mv_{\bot }^{2}/2B$
and there is a non-adiabatic contribution of the form
$mv_{\bot }^{2}/2B$
and there is a non-adiabatic contribution of the form
 $A\exp (-{\it\alpha}/{\it\epsilon})\cos {\it\phi}$
.
$A\exp (-{\it\alpha}/{\it\epsilon})\cos {\it\phi}$
.
A convenient starting point for calculating the power series is the Vlasov equation
for a distribution of particles (see § 1.3).
(Its connection with the invariants is, of course, that if
![]() $I_{j}$
are invariants, then
$I_{j}$
are invariants, then
![]() $f(I_{j})$
is a stationary distribution.)
$f(I_{j})$
is a stationary distribution.)
Introducing the gyro-phase angle
![]() ${\it\phi}$
about the magnetic field, the energy
${\it\phi}$
about the magnetic field, the energy
![]() ${\it\epsilon}$
and the magnetic moment
${\it\epsilon}$
and the magnetic moment
![]() ${\it\mu}$
as velocity coordinates, and
${\it\mu}$
as velocity coordinates, and
 $({\it\alpha},{\it\beta},s)$
as spatial coordinates (
$({\it\alpha},{\it\beta},s)$
as spatial coordinates (
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
label a field line as in § 2.1 and
${\it\beta}$
label a field line as in § 2.1 and
![]() $s$
is the distance along it), the Vlasov equation
$s$
is the distance along it), the Vlasov equation
 $$\begin{eqnarray}\frac{\partial f}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f+\frac{e_{s}}{m_{s}}(\boldsymbol{v}\times \boldsymbol{B})\boldsymbol{\cdot }\frac{\partial f}{\partial \boldsymbol{v}}=0\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f+\frac{e_{s}}{m_{s}}(\boldsymbol{v}\times \boldsymbol{B})\boldsymbol{\cdot }\frac{\partial f}{\partial \boldsymbol{v}}=0\end{eqnarray}$$
can be written as
 $$\begin{eqnarray}\frac{\partial f}{\partial {\it\phi}}={\it\lambda}\left(Df+\frac{1}{B}\frac{\partial f}{\partial t}\right).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f}{\partial {\it\phi}}={\it\lambda}\left(Df+\frac{1}{B}\frac{\partial f}{\partial t}\right).\end{eqnarray}$$
Here
![]() $D$
is a partial differential operator in
$D$
is a partial differential operator in
 $({\it\phi},{\it\mu},{\it\alpha},{\it\beta},s)$
, with coefficients depending on the gradients, curvature and
torsion of the field lines.
$({\it\phi},{\it\mu},{\it\alpha},{\it\beta},s)$
, with coefficients depending on the gradients, curvature and
torsion of the field lines.
We now seek a solution of (16.31),
 $$\begin{eqnarray}f=\,f_{0}+{\it\lambda}\,f_{1}+{\it\lambda}^{2}f_{2}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}f=\,f_{0}+{\it\lambda}\,f_{1}+{\it\lambda}^{2}f_{2}+\cdots \,,\end{eqnarray}$$
that is stationary on ever increasing time scales,
 $t,t/{\it\lambda},t/{\it\lambda}^{2},\dots$
. It turns out (as detailed in Hastie et al.
Reference Hastie, Taylor and Haas1967) that a distribution is stationary on
all scales if it depends only on three variables – the energy
$t,t/{\it\lambda},t/{\it\lambda}^{2},\dots$
. It turns out (as detailed in Hastie et al.
Reference Hastie, Taylor and Haas1967) that a distribution is stationary on
all scales if it depends only on three variables – the energy
![]() ${\it\epsilon}$
, the magnetic moment
${\it\epsilon}$
, the magnetic moment
 ${\it\mu}_{0}=mv_{\bot }^{2}/2B$
, and a longitudinal invariant
${\it\mu}_{0}=mv_{\bot }^{2}/2B$
, and a longitudinal invariant
 $$\begin{eqnarray}J_{0}=\oint v_{\Vert }\,\text{d}s=\oint ({\it\epsilon}-{\it\mu}_{0}B)^{1/2}\,\text{d}s.\end{eqnarray}$$
$$\begin{eqnarray}J_{0}=\oint v_{\Vert }\,\text{d}s=\oint ({\it\epsilon}-{\it\mu}_{0}B)^{1/2}\,\text{d}s.\end{eqnarray}$$
The latter is associated with periodic motion along the field (between magnetic mirrors for trapped particles or around closed field lines for passing particles in a torus).
If we now write the true invariants
![]() $\hat{{\it\mu}}$
and
$\hat{{\it\mu}}$
and
![]() ${\hat{J}}$
as
${\hat{J}}$
as
 $$\begin{eqnarray}\displaystyle & \hat{{\it\mu}}={\it\mu}_{0}+{\it\lambda}{\it\mu}_{1}+{\it\lambda}^{2}{\it\mu}_{2}+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \hat{{\it\mu}}={\it\mu}_{0}+{\it\lambda}{\it\mu}_{1}+{\it\lambda}^{2}{\it\mu}_{2}+\cdots \,, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\hat{J}}=J_{0}+{\it\lambda}J_{1}+{\it\lambda}^{2}J_{2}+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\hat{J}}=J_{0}+{\it\lambda}J_{1}+{\it\lambda}^{2}J_{2}+\cdots \,, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}f({\it\mu}_{0},J_{0},{\it\epsilon})+{\it\lambda}\left({\it\mu}_{1}\frac{\partial f}{\partial {\it\mu}_{0}}+J_{1}\frac{\partial f}{\partial J_{0}}\right)+{\it\lambda}^{2}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}f({\it\mu}_{0},J_{0},{\it\epsilon})+{\it\lambda}\left({\it\mu}_{1}\frac{\partial f}{\partial {\it\mu}_{0}}+J_{1}\frac{\partial f}{\partial J_{0}}\right)+{\it\lambda}^{2}+\cdots \,,\end{eqnarray}$$
we obtain a recursion equation for the higher-order terms in the
invariants
![]() $\hat{{\it\mu}}$
and
$\hat{{\it\mu}}$
and
![]() ${\hat{J}}$
:
${\hat{J}}$
:
 $$\begin{eqnarray}\left\{\begin{array}{@{}c@{}}J_{n+1}\\ {\it\mu}_{n+1}\end{array}\right\}=\int D\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}-{\it\sigma}\int _{s_{0}}^{s}\frac{B\,\text{d}s}{q}L\,\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}+\int \frac{\text{d}{\it\alpha}}{\partial J/\partial {\it\alpha}}H\,\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}c@{}}J_{n+1}\\ {\it\mu}_{n+1}\end{array}\right\}=\int D\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}-{\it\sigma}\int _{s_{0}}^{s}\frac{B\,\text{d}s}{q}L\,\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}+\int \frac{\text{d}{\it\alpha}}{\partial J/\partial {\it\alpha}}H\,\left\{\begin{array}{@{}c@{}}J_{n}\\ {\it\mu}_{n}\end{array}\right\}.\end{eqnarray}$$
Here
![]() $D$
is the Vlasov operator (16.31),
$D$
is the Vlasov operator (16.31),
![]() $L$
and
$L$
and
![]() $H$
are iterates of it, and
$H$
are iterates of it, and
![]() ${\it\sigma}=\pm 1$
distinguishes the two possible directions of
${\it\sigma}=\pm 1$
distinguishes the two possible directions of
![]() $v_{\Vert }$
. The first few terms,
$v_{\Vert }$
. The first few terms,
![]() ${\it\mu}_{1}$
,
${\it\mu}_{1}$
,
![]() ${\it\mu}_{2}$
and
${\it\mu}_{2}$
and
![]() $J_{1}$
, of the invariants are given in Hastie et al.
(Reference Hastie, Taylor and Haas1967). An unexpected feature is that they
depend on the direction
$J_{1}$
, of the invariants are given in Hastie et al.
(Reference Hastie, Taylor and Haas1967). An unexpected feature is that they
depend on the direction
![]() ${\it\sigma}$
of the particle motion along the magnetic field.
${\it\sigma}$
of the particle motion along the magnetic field.
It is not clear that a rigorous calculation of the non-adiabatic contribution to
![]() ${\it\mu}$
exists for particles in a spatially varying field. Some
calculations of it essentially replace the motion in a spatially varying field
${\it\mu}$
exists for particles in a spatially varying field. Some
calculations of it essentially replace the motion in a spatially varying field
![]() $B(\boldsymbol{r})$
by motion in a fictitious time-dependent field
$B(\boldsymbol{r})$
by motion in a fictitious time-dependent field
![]() $B^{\ast }(t)$
– taken to be the field at the guiding centre of the particle, i.e.
$B^{\ast }(t)$
– taken to be the field at the guiding centre of the particle, i.e.
 $\text{d}B^{\ast }/\text{d}t=v_{\Vert }\,\partial B/\partial s$
. This, of course, leads to the exponential form (16.24) dependent on a complex zero of
$\text{d}B^{\ast }/\text{d}t=v_{\Vert }\,\partial B/\partial s$
. This, of course, leads to the exponential form (16.24) dependent on a complex zero of
![]() $B^{\ast }(t)$
. (The uncertainty about such a calculation lies in the fact that we
are trying to calculate an exponentially small quantity when the guiding centre orbit
is only accurate to order
$B^{\ast }(t)$
. (The uncertainty about such a calculation lies in the fact that we
are trying to calculate an exponentially small quantity when the guiding centre orbit
is only accurate to order
![]() ${\it\epsilon}$
, a larger quantity. Moreover, whereas a particle in a slowly
time-varying field experiences only the slow variation in
${\it\epsilon}$
, a larger quantity. Moreover, whereas a particle in a slowly
time-varying field experiences only the slow variation in
![]() $B(t)$
, a particle in a spatially varying field also experiences a ‘fast’
variation around the Larmor orbit.)
$B(t)$
, a particle in a spatially varying field also experiences a ‘fast’
variation around the Larmor orbit.)
16.3. Orbit calculations
The magnetic moment is clearly the most important invariant for plasma confinement in mirrors, and it is interesting therefore to see its behaviour in particle orbits computed in a non-uniform field. This is illustrated in figure 48(a–c), reproduced from Hastie et al. (Reference Hastie, Hobbs and Taylor1969). (Actually, these are for orbits in a quadrupole field, as shown in figure 47, whose strength is given by
 $$\begin{eqnarray}B=\frac{2I}{aq}(1+2q\cos {\it\Phi}+q^{2})^{1/4},\end{eqnarray}$$
$$\begin{eqnarray}B=\frac{2I}{aq}(1+2q\cos {\it\Phi}+q^{2})^{1/4},\end{eqnarray}$$
so that
![]() ${\it\Phi}={\rm\pi}$
is the weak-field plane of symmetry,
${\it\Phi}={\rm\pi}$
is the weak-field plane of symmetry,
![]() $2a$
is the separation between the current filaments and
$2a$
is the separation between the current filaments and
![]() $q$
labels field lines. In such a field there are both trapped orbits,
near the weak-field plane, and untrapped circulating orbits.)
$q$
labels field lines. In such a field there are both trapped orbits,
near the weak-field plane, and untrapped circulating orbits.)

Figure 47. Quadrupole field configuration (from Hastie Reference Hastie and Dendy1993).
Figure 48(a) shows the change
in the magnetic moment invariant, calculated from the approximations
 ${\it\mu}_{0},~({\it\mu}_{0}+{\it\lambda}{\it\mu}_{1})$
and
${\it\mu}_{0},~({\it\mu}_{0}+{\it\lambda}{\it\mu}_{1})$
and
 $({\it\mu}_{0}+{\it\lambda}{\it\mu}_{1}+{\it\lambda}^{2}{\it\mu}_{2})$
to the infinite power series (16.34). This orbit starts at the weak-field plane and makes
two reflections and two transits of the weak-field plane. The lowest approximation
$({\it\mu}_{0}+{\it\lambda}{\it\mu}_{1}+{\it\lambda}^{2}{\it\mu}_{2})$
to the infinite power series (16.34). This orbit starts at the weak-field plane and makes
two reflections and two transits of the weak-field plane. The lowest approximation
 ${\it\mu}_{0}=mv_{\bot }^{2}/2B$
shows significant oscillations between transits and larger ‘jumps’
as it crosses the weak-field plane. As higher-order terms are added to the power
series, the oscillations disappear, but the ‘jumps’ remain.
${\it\mu}_{0}=mv_{\bot }^{2}/2B$
shows significant oscillations between transits and larger ‘jumps’
as it crosses the weak-field plane. As higher-order terms are added to the power
series, the oscillations disappear, but the ‘jumps’ remain.

Figure 48. (a) Evolution of successive approximations to the particle
magnetic moment as it moves in a mirror field.
(b) Exponential form of the non-adiabatic jump at each
transit as a function of
 $a/r_{L}\propto 1/v$
. (c) Long-time behaviour of a
non-adiabatic particle. Here
$a/r_{L}\propto 1/v$
. (c) Long-time behaviour of a
non-adiabatic particle. Here
 $q=1.19$
,
$q=1.19$
,
![]() ${\it\Phi}={\rm\pi}$
and
${\it\Phi}={\rm\pi}$
and
 $r/a=0.075$
. (Reproduced with permission from Hastie
et al. (Reference Hastie, Hobbs and Taylor1969).)
$r/a=0.075$
. (Reproduced with permission from Hastie
et al. (Reference Hastie, Hobbs and Taylor1969).)
The exponential form of these non-adiabatic jumps is confirmed by figure 48(b). (More extensive calculations of these jumps can be found in Howard (Reference Howard1971).)
Figure 48(c) shows the non-adiabatic changes over many transits of the weak-field plane. Owing to the large number of Larmor cycles that occur between successive transits, the phase at each transit is effectively random. After several transits, the particle is scattered from a trapped orbit to a passing one and back again (the boundary between trapped and passing orbits is shown by the dashed line).
It should be clearly understood that the parameters for these calculations were chosen to illustrate the points of interest and are not representative of typical mirror machines.
Finally, we should note that there is actually another invariant, in addition to
![]() $\hat{{\it\mu}}$
and
$\hat{{\it\mu}}$
and
![]() ${\hat{J}}$
, for a particle in a mirror machine, associated with the periodic
orbit of the guiding centre as it drifts around the axis of symmetry. The invariant
in this case is the magnetic flux enclosed by the drift orbit. However, it is seldom
invoked, as the drift motion can be studied directly (see § 20).
${\hat{J}}$
, for a particle in a mirror machine, associated with the periodic
orbit of the guiding centre as it drifts around the axis of symmetry. The invariant
in this case is the magnetic flux enclosed by the drift orbit. However, it is seldom
invoked, as the drift motion can be studied directly (see § 20).
16.4. Summary
Adiabatic invariants are subtle quantities, and in the case of charged particles in a
non-uniform magnetic field they are complicated functions of the field gradient,
curvature and torsion. However, in practice, provided the Larmor radius is everywhere
much smaller than the local field gradient
 $R=(\boldsymbol{{\rm\nabla}}B/B)^{-1}$
, the magnetic moment is effectively constant – apart from the
effect of collisions.
$R=(\boldsymbol{{\rm\nabla}}B/B)^{-1}$
, the magnetic moment is effectively constant – apart from the
effect of collisions.
17. Simple mirror machines
On the basis of the guiding centre drifts (see § 1.3) and the invariance of the magnetic moment, an axisymmetric mirror
machine, such as that shown in figure 46, should
confine a low-
![]() ${\it\beta}$
plasma (
${\it\beta}$
plasma (
![]() ${\it\beta}$
= plasma pressure/magnetic pressure). The drifts are azimuthal and
cause no direct loss, the mirrors confine particles (except for those within the loss
cone) and the magnetic field is created solely by external coils and is therefore
unconditionally stable!
${\it\beta}$
= plasma pressure/magnetic pressure). The drifts are azimuthal and
cause no direct loss, the mirrors confine particles (except for those within the loss
cone) and the magnetic field is created solely by external coils and is therefore
unconditionally stable!
Unfortunately, there are two serious problems with this simple picture. The first is
that collisions cause particles to be scattered into the loss cone. This is a more
complex problem than it may appear at first sight (Post Reference Post, Post, Baldwin and Ryutov1983, Reference Post1987). Electrons are scattered
much faster than ions; therefore an electrostatic potential builds up, which narrows the
loss cone for electrons (in fact they are essentially confined electrostatically) and
widens it for ions. Also, the loss cone varies with the local field strength and
therefore with the shape of the field – so the loss does not depend solely on the mirror
ratio,
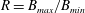 $R=B_{max}/B_{min}$
. Nevertheless, as the result of several computations, it appears that
the confinement time set by scattering is a few ion–ion collision times
$R=B_{max}/B_{min}$
. Nevertheless, as the result of several computations, it appears that
the confinement time set by scattering is a few ion–ion collision times
![]() ${\it\tau}_{ii}$
, and varies very slowly with the mirror ratio. A popular fit to the
computations is
${\it\tau}_{ii}$
, and varies very slowly with the mirror ratio. A popular fit to the
computations is
 $$\begin{eqnarray}{\it\tau}_{c}\sim {\it\tau}_{ii}\log _{10}R.\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{c}\sim {\it\tau}_{ii}\log _{10}R.\end{eqnarray}$$
In contrast, the confinement in toroidal systems can be many collision
times,
 ${\it\tau}_{c}\sim {\it\tau}_{ii}(a^{2}/{\it\rho}_{i}^{2})$
.
${\it\tau}_{c}\sim {\it\tau}_{ii}(a^{2}/{\it\rho}_{i}^{2})$
.
The second serious problem for mirror machines is that the system is unstable
even at low plasma pressure. This instability arises in the
following way (see figure 49). At low
![]() ${\it\beta}$
the plasma does not have enough energy to distort the near-vacuum
magnetic field. Consequently, any perturbation must take the form of a flute-like ridge,
aligned with the magnetic field (as shown in cross-section in figure 49
a). Then the azimuthal grad
${\it\beta}$
the plasma does not have enough energy to distort the near-vacuum
magnetic field. Consequently, any perturbation must take the form of a flute-like ridge,
aligned with the magnetic field (as shown in cross-section in figure 49
a). Then the azimuthal grad
![]() $B$
drifts of ions and electrons, in opposite directions, produce a space
charge along the sides of the ridge. This in turn produces an electric field, such that
the ensuing
$B$
drifts of ions and electrons, in opposite directions, produce a space
charge along the sides of the ridge. This in turn produces an electric field, such that
the ensuing
![]() $E\times B$
drift increases the amplitude of the deformation. The
direction of the drifts is set by the fact that the magnetic field in a simple mirror,
since it is essentially a vacuum field, always decreases with distance
from the axis, at least in the centre of the machine.
$E\times B$
drift increases the amplitude of the deformation. The
direction of the drifts is set by the fact that the magnetic field in a simple mirror,
since it is essentially a vacuum field, always decreases with distance
from the axis, at least in the centre of the machine.

Figure 49. Development of the flute instability in a mirror machine (from Taylor Reference Taylor1968); see text for details.
This simple picture already suggests a cure for the instability. If the radial field
gradient were reversed, the grad
![]() $B$
drift, and therefore the
$B$
drift, and therefore the
![]() $E\times B$
drift, would reverse, and the growth of any ridge-like deformation
would be suppressed rather than amplified.
$E\times B$
drift, would reverse, and the growth of any ridge-like deformation
would be suppressed rather than amplified.
The recipe for stability in a mirror machine is therefore that the magnetic field should
increase in the radial as well as in the axial direction. In fact, we shall investigate
fields that increase in all directions from a non-zero minimum. Such fields are now
known as minimum-
![]() $B$
fields or magnetic wells. (Note that, although the field in an
axisymmetric ‘spindle’ cusp increases in all directions from its centre (see
figure 50), it is not classed as a ‘minimum-
$B$
fields or magnetic wells. (Note that, although the field in an
axisymmetric ‘spindle’ cusp increases in all directions from its centre (see
figure 50), it is not classed as a ‘minimum-
![]() $B$
’ field, as its minimum is zero. Consequently, the criterion for
adiabatic invariance of the magnetic moment cannot be satisfied there.)
$B$
’ field, as its minimum is zero. Consequently, the criterion for
adiabatic invariance of the magnetic moment cannot be satisfied there.)

Figure 50. Sketch of spindle cusp configuration.
The problem with this prescription for stability is that one cannot create an
axisymmetric vacuum field with the minimum-
![]() $B$
property. Axisymmetry is desirable because the grad
$B$
property. Axisymmetry is desirable because the grad
![]() $B$
drifts then obviously close and do not lead to particle loss. However,
this simplification must be abandoned.
$B$
drifts then obviously close and do not lead to particle loss. However,
this simplification must be abandoned.
The simplest, non-axisymmetric minimum-
![]() $B$
field is created by adding ‘Ioffe bars’ to the simple mirrors (Gott
et al.
Reference Gott, Ioffe and Tel’kovskii1962), as shown in figure 51.
$B$
field is created by adding ‘Ioffe bars’ to the simple mirrors (Gott
et al.
Reference Gott, Ioffe and Tel’kovskii1962), as shown in figure 51.
Near the axis the field due to the bars is
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{r}=-\frac{4I}{R}\left(\frac{r}{R}\right)\cos 2{\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{r}=-\frac{4I}{R}\left(\frac{r}{R}\right)\cos 2{\it\theta}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}=\frac{4I}{R}\left(\frac{r}{R}\right)\sin 2{\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}=\frac{4I}{R}\left(\frac{r}{R}\right)\sin 2{\it\theta}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{z}=B_{0}\left[1-{\it\alpha}\,\text{I}_{0}\left(\frac{2{\rm\pi}r}{L}\right)\cos \left(\frac{2{\rm\pi}z}{L}\right)\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{z}=B_{0}\left[1-{\it\alpha}\,\text{I}_{0}\left(\frac{2{\rm\pi}r}{L}\right)\cos \left(\frac{2{\rm\pi}z}{L}\right)\right], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}=-{\it\alpha}B_{0}\,\text{I}_{1}\left(\frac{2{\rm\pi}r}{L}\right)\sin \left(\frac{2{\rm\pi}z}{L}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{{\it\theta}}=-{\it\alpha}B_{0}\,\text{I}_{1}\left(\frac{2{\rm\pi}r}{L}\right)\sin \left(\frac{2{\rm\pi}z}{L}\right), & \displaystyle\end{eqnarray}$$
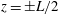 $z=\pm L/2$
, the mirror ratio
$z=\pm L/2$
, the mirror ratio
 $R=(1+{\it\alpha})/(1-{\it\alpha})$
, and the field strength near the axis is
$R=(1+{\it\alpha})/(1-{\it\alpha})$
, and the field strength near the axis is  $$\begin{eqnarray}B^{2}=B_{0}^{2}(1-{\it\alpha})^{2}+4{\rm\pi}^{2}B_{0}^{2}\left\{{\it\alpha}(1-{\it\alpha})\frac{z^{2}}{L^{2}}+\frac{r^{2}}{L^{2}}\left[\frac{4I^{2}L^{2}}{{\rm\pi}^{2}B_{0}^{2}R^{4}}-\frac{{\it\alpha}(1-{\it\alpha})}{2}\right]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}B^{2}=B_{0}^{2}(1-{\it\alpha})^{2}+4{\rm\pi}^{2}B_{0}^{2}\left\{{\it\alpha}(1-{\it\alpha})\frac{z^{2}}{L^{2}}+\frac{r^{2}}{L^{2}}\left[\frac{4I^{2}L^{2}}{{\rm\pi}^{2}B_{0}^{2}R^{4}}-\frac{{\it\alpha}(1-{\it\alpha})}{2}\right]\right\}.\end{eqnarray}$$
As the current in the bars is increased, when
 $$\begin{eqnarray}I^{2}>\frac{{\rm\pi}^{2}R^{4}}{8L^{2}}{\it\alpha}(1-{\it\alpha})B_{0}^{2},\end{eqnarray}$$
$$\begin{eqnarray}I^{2}>\frac{{\rm\pi}^{2}R^{4}}{8L^{2}}{\it\alpha}(1-{\it\alpha})B_{0}^{2},\end{eqnarray}$$
the ‘magnetic isobars’, on which
 $|\boldsymbol{B}|=\text{constant}$
, change from open hyperboloids to closed ellipsoids – the classic minimum-
$|\boldsymbol{B}|=\text{constant}$
, change from open hyperboloids to closed ellipsoids – the classic minimum-
![]() $B$
configuration. This change in the isobars is shown in figure 52.
$B$
configuration. This change in the isobars is shown in figure 52.

Figure 51. (a) Mirror machine stabilisation by Ioffe bars and (b) the resulting magnetic field (from Taylor Reference Taylor1968).

Figure 52. Magnetic isobars in a stabilised minimum-
![]() $B$
mirror device for (a) small current in the
stabilising rods and (b) large current in the rods
(from Taylor Reference Taylor1968).
$B$
mirror device for (a) small current in the
stabilising rods and (b) large current in the rods
(from Taylor Reference Taylor1968).
A similar minimum-
![]() $B$
configuration can be formed from a single coil – the ‘tennis ball
seam’ (see figure 53). (This was invented at
Culham and independently at Livermore – where of course it was dubbed the ‘baseball
seam’!)
$B$
configuration can be formed from a single coil – the ‘tennis ball
seam’ (see figure 53). (This was invented at
Culham and independently at Livermore – where of course it was dubbed the ‘baseball
seam’!)

Figure 53. Schematic of the tennis ball coil and field lines. (Reproduced with permission from Post (Reference Post1987).)
A fundamental problem with the field created by the Ioffe bars or the tennis ball coil is the complicated particle drift orbits – it is far from clear that the orbits are closed or that confinement and charge neutrality are maintained.
An important step therefore is the realisation (Taylor Reference Taylor1963, Reference Taylor1965) that containment and
stability in magnetic wells can be described solely in terms of their basic property:
that the magnetic isobars form a set of closed, nested surfaces surrounding a non-zero
minimum of
![]() $|\boldsymbol{B}|$
. (Note that the magnetic isobars are not flux surfaces. In general, a
line of force will cut a magnetic isobar twice, or not at all.)
$|\boldsymbol{B}|$
. (Note that the magnetic isobars are not flux surfaces. In general, a
line of force will cut a magnetic isobar twice, or not at all.)
18. Equilibria in magnetic wells
18.1. Fluid picture
For equilibrium in minimum-
![]() $B$
systems, the pressure tensor,
$B$
systems, the pressure tensor,
 $$\begin{eqnarray}\unicode[STIX]{x1D64B}=p_{\bot }\unicode[STIX]{x1D644}+(p_{\Vert }-p_{\bot })\boldsymbol{n}\boldsymbol{n},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64B}=p_{\bot }\unicode[STIX]{x1D644}+(p_{\Vert }-p_{\bot })\boldsymbol{n}\boldsymbol{n},\end{eqnarray}$$
which is diagonal but not isotropic, must satisfy (see § 1.3)
 $$\begin{eqnarray}\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D64B},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}\times \boldsymbol{B}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D64B},\end{eqnarray}$$
where
![]() $\boldsymbol{n}$
is a unit vector in the direction of
$\boldsymbol{n}$
is a unit vector in the direction of
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\unicode[STIX]{x1D644}$
is the unit tensor. From the parallel component of this, we find a
condition on the pressure,
$\unicode[STIX]{x1D644}$
is the unit tensor. From the parallel component of this, we find a
condition on the pressure,
 $$\begin{eqnarray}\frac{\partial p_{\Vert }}{\partial s}+\frac{(p_{\bot }-p_{\Vert })}{B}\frac{\partial B}{\partial s}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial p_{\Vert }}{\partial s}+\frac{(p_{\bot }-p_{\Vert })}{B}\frac{\partial B}{\partial s}=0,\end{eqnarray}$$
where
![]() $s$
is distance along the field.
$s$
is distance along the field.
If (18.3) is satisfied, we can
solve (18.2) for
![]() $\boldsymbol{j}_{\bot }$
,
$\boldsymbol{j}_{\bot }$
,
 $$\begin{eqnarray}\boldsymbol{j}_{\bot }=-\frac{\boldsymbol{{\rm\nabla}}p_{\bot }\times \boldsymbol{B}}{B^{2}}+\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[(p_{\Vert }-p_{\bot })\boldsymbol{n}\boldsymbol{n}]}{B^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}_{\bot }=-\frac{\boldsymbol{{\rm\nabla}}p_{\bot }\times \boldsymbol{B}}{B^{2}}+\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[(p_{\Vert }-p_{\bot })\boldsymbol{n}\boldsymbol{n}]}{B^{2}}.\end{eqnarray}$$
Charge neutrality then imposes a restriction on
![]() $\boldsymbol{j}_{\Vert }={\it\lambda}\boldsymbol{B}$
, as in § 2,
$\boldsymbol{j}_{\Vert }={\it\lambda}\boldsymbol{B}$
, as in § 2,
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{\Vert }=\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{\bot },\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{\Vert }=\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{\bot },\end{eqnarray}$$
which after some manipulation leads to
 $$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}(p_{\bot }+p_{\Vert })\boldsymbol{\cdot }\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\lambda}=-\boldsymbol{{\rm\nabla}}(p_{\bot }+p_{\Vert })\boldsymbol{\cdot }\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{3}}.\end{eqnarray}$$
Integrating this from the point at which a line of force enters the plasma to the point at which it leaves thus gives the constraint
 $$\begin{eqnarray}\int \boldsymbol{{\rm\nabla}}(p_{\bot }+p_{\Vert })\boldsymbol{\cdot }\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{4}}\,\text{d}s=0.\end{eqnarray}$$
$$\begin{eqnarray}\int \boldsymbol{{\rm\nabla}}(p_{\bot }+p_{\Vert })\boldsymbol{\cdot }\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{4}}\,\text{d}s=0.\end{eqnarray}$$
If this were not satisfied, there would be currents in the plasma-free region or accumulations of charge in the plasma region.
The constraint (18.7) is automatically satisfied in an axisymmetric system, but in non-axisymmetric systems it is a powerful restriction.
18.2. Particle picture
If
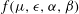 $f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
is the distribution of guiding centres on a field line
$f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
is the distribution of guiding centres on a field line
![]() ${\it\alpha},{\it\beta}$
, then the local density along that line is
${\it\alpha},{\it\beta}$
, then the local density along that line is
 $$\begin{eqnarray}\int f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})\frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon},\end{eqnarray}$$
$$\begin{eqnarray}\int f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})\frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon},\end{eqnarray}$$
and the pressure tensor is therefore
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{\bot }=\int \text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})\frac{{\it\mu}B^{2}}{2({\it\epsilon}-{\it\mu}B)^{1/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{\bot }=\int \text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})\frac{{\it\mu}B^{2}}{2({\it\epsilon}-{\it\mu}B)^{1/2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{\Vert }=\int \text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})B({\it\epsilon}-{\it\mu}B)^{1/2}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{\Vert }=\int \text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})B({\it\epsilon}-{\it\mu}B)^{1/2}. & \displaystyle\end{eqnarray}$$
The second constraint (18.7), which
restricts the function
 $f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
, can be reinterpreted in terms of particle drifts as
$f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
, can be reinterpreted in terms of particle drifts as
 $$\begin{eqnarray}\int (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{D})\frac{\text{d}l}{B}=0,\end{eqnarray}$$
$$\begin{eqnarray}\int (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\,\boldsymbol{j}_{D})\frac{\text{d}l}{B}=0,\end{eqnarray}$$
where the diamagnetic current
![]() $\boldsymbol{j}_{D}$
is given by the sum over species of the grad
$\boldsymbol{j}_{D}$
is given by the sum over species of the grad
![]() $B$
drift velocities,
$B$
drift velocities,
 $$\begin{eqnarray}\boldsymbol{v}_{B}=-\frac{m_{s}}{e_{s}}\frac{\boldsymbol{{\rm\nabla}}B\times \boldsymbol{B}}{B^{3}}(2{\it\epsilon}-{\it\mu}B).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{B}=-\frac{m_{s}}{e_{s}}\frac{\boldsymbol{{\rm\nabla}}B\times \boldsymbol{B}}{B^{3}}(2{\it\epsilon}-{\it\mu}B).\end{eqnarray}$$
This current due to guiding centre drifts is not the total current – there is also a current due to the gradient in density of guiding centres. However, this can be expressed as the curl of the magnetisation per unit volume and is therefore divergence-free.
18.3. Special minimum-
 $B$
equilibria
$B$
equilibria
A class of equilibria that satisfy (18.7) are those for which
 $(p_{\bot }+p_{\Vert })$
is a function of the field strength
$(p_{\bot }+p_{\Vert })$
is a function of the field strength
![]() $B$
only. Then the parallel constraint (18.3) makes
$B$
only. Then the parallel constraint (18.3) makes
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
separately functions of
$p_{\Vert }$
separately functions of
![]() $B$
only. Thus
$B$
only. Thus
 $p_{\bot }=p_{\bot }(B)$
,
$p_{\bot }=p_{\bot }(B)$
,
 $p_{\Vert }=p_{\Vert }(B)$
and
$p_{\Vert }=p_{\Vert }(B)$
and
 $Bp_{\Vert }^{\prime }=p_{\Vert }-p_{\bot }$
. Either of the two functions,
$Bp_{\Vert }^{\prime }=p_{\Vert }-p_{\bot }$
. Either of the two functions,
![]() $p_{\bot }(B)$
or
$p_{\bot }(B)$
or
![]() $p_{\Vert }(B)$
, can be chosen arbitrarily, but the other is then fixed by the
parallel equilibrium constraint. In terms of a particle description of the plasma,
these special equilibria are those in which the distribution function
$p_{\Vert }(B)$
, can be chosen arbitrarily, but the other is then fixed by the
parallel equilibrium constraint. In terms of a particle description of the plasma,
these special equilibria are those in which the distribution function
 $f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
is independent of
$f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
is independent of
![]() ${\it\alpha},{\it\beta}$
, that is,
${\it\alpha},{\it\beta}$
, that is,
 $f\equiv f({\it\mu},{\it\epsilon})$
.
$f\equiv f({\it\mu},{\it\epsilon})$
.
The significance of magnetic fields that possess closed magnetic isobars is now
apparent. Equilibria in which
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
are functions of
$p_{\Vert }$
are functions of
![]() $B$
may exist in many field configurations, but only in those which
possess closed magnetic isobars can these equilibria represent
confined plasmas. (We will examine their stability in the next
section.)
$B$
may exist in many field configurations, but only in those which
possess closed magnetic isobars can these equilibria represent
confined plasmas. (We will examine their stability in the next
section.)
A simple example of this class of equilibria is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \!\left.\begin{array}{@{}l@{}}p_{\Vert }=cB(B_{0}-B)^{n}\\ p_{\bot }=ncB^{2}(B_{0}-B)^{n-1}\end{array}\right\}\quad \text{for }B<B_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \!\left.\begin{array}{@{}l@{}}p_{\Vert }=cB(B_{0}-B)^{n}\\ p_{\bot }=ncB^{2}(B_{0}-B)^{n-1}\end{array}\right\}\quad \text{for }B<B_{0},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle p_{\bot }=p_{\Vert }=0\hspace{64.20007pt}\text{for }B>B_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle p_{\bot }=p_{\Vert }=0\hspace{64.20007pt}\text{for }B>B_{0}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle f({\it\mu},{\it\epsilon}) & = & \displaystyle g({\it\mu})({\it\mu}B_{0}-{\it\epsilon})^{n-3/2}\quad \text{for }{\it\epsilon}<{\it\mu}B_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\mu},{\it\epsilon}) & = & \displaystyle g({\it\mu})({\it\mu}B_{0}-{\it\epsilon})^{n-3/2}\quad \text{for }{\it\epsilon}<{\it\mu}B_{0},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle f({\it\mu},{\it\epsilon}) & = & \displaystyle 0\hspace{90.0pt}\text{for }{\it\epsilon}>{\it\mu}B_{0}~\text{(the loss cone)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\mu},{\it\epsilon}) & = & \displaystyle 0\hspace{90.0pt}\text{for }{\it\epsilon}>{\it\mu}B_{0}~\text{(the loss cone)},\end{eqnarray}$$
19. Energy principles and stability
One of the most useful ways of investigating plasma stability is by means of ‘energy principles’. From the mathematical point of view, these principles have some subtle and questionable features, but the underlying concept is straightforward.
Consider first the case of a scalar pressure plasma, with an adiabatic equation of state
(see § 1.3, now setting the free-space
permeability
![]() ${\it\mu}_{0}\equiv 1$
for clarity). The equations governing linear perturbations of a static
equilibrium are then
${\it\mu}_{0}\equiv 1$
for clarity). The equations governing linear perturbations of a static
equilibrium are then
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\frac{\partial \boldsymbol{v}_{1}}{\partial t}=\,\boldsymbol{j}_{1}\times \boldsymbol{B}+\,\boldsymbol{j}\times \boldsymbol{B}_{1}-\boldsymbol{{\rm\nabla}}p_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\frac{\partial \boldsymbol{v}_{1}}{\partial t}=\,\boldsymbol{j}_{1}\times \boldsymbol{B}+\,\boldsymbol{j}\times \boldsymbol{B}_{1}-\boldsymbol{{\rm\nabla}}p_{1}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial p_{1}}{\partial t}=-\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p-{\it\gamma}p\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial p_{1}}{\partial t}=-\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p-{\it\gamma}p\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{B}_{1}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}_{1}\times \boldsymbol{B}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{B}_{1}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}_{1}\times \boldsymbol{B}). & \displaystyle\end{eqnarray}$$
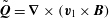 $\tilde{\boldsymbol{Q}}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}_{1}\times \boldsymbol{B})$
,
$\tilde{\boldsymbol{Q}}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{v}_{1}\times \boldsymbol{B})$
,  $$\begin{eqnarray}{\it\rho}\frac{\partial ^{2}\boldsymbol{v}_{1}}{\partial t^{2}}=(\boldsymbol{{\rm\nabla}}\times \tilde{\boldsymbol{Q}})\times \boldsymbol{B}+\,\boldsymbol{j}\times \tilde{\boldsymbol{Q}}+\boldsymbol{{\rm\nabla}}(\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+{\it\gamma}p\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\rho}\frac{\partial ^{2}\boldsymbol{v}_{1}}{\partial t^{2}}=(\boldsymbol{{\rm\nabla}}\times \tilde{\boldsymbol{Q}})\times \boldsymbol{B}+\,\boldsymbol{j}\times \tilde{\boldsymbol{Q}}+\boldsymbol{{\rm\nabla}}(\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+{\it\gamma}p\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}_{1}).\end{eqnarray}$$
If the perturbation takes the form of a normal mode,
 $\boldsymbol{v}_{1}=\text{i}{\it\omega}{\bf\xi}(\boldsymbol{x})\exp (-\text{i}{\it\omega}t)$
, where
$\boldsymbol{v}_{1}=\text{i}{\it\omega}{\bf\xi}(\boldsymbol{x})\exp (-\text{i}{\it\omega}t)$
, where
![]() ${\bf\xi}$
is the plasma displacement, the equation of motion becomes
${\bf\xi}$
is the plasma displacement, the equation of motion becomes
 $$\begin{eqnarray}-{\it\omega}^{2}{\it\rho}{\bf\xi}=\boldsymbol{F}({\bf\xi}).\end{eqnarray}$$
$$\begin{eqnarray}-{\it\omega}^{2}{\it\rho}{\bf\xi}=\boldsymbol{F}({\bf\xi}).\end{eqnarray}$$
It can be shown that
![]() $\boldsymbol{F}({\bf\xi})$
is self-adjoint (see Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kulsrud1958; Freidberg, Reference Freidberg1987), and therefore
$\boldsymbol{F}({\bf\xi})$
is self-adjoint (see Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kulsrud1958; Freidberg, Reference Freidberg1987), and therefore
 $$\begin{eqnarray}{\it\omega}^{2}\int _{V}{\it\rho}|{\bf\xi}|^{2}\,\text{d}{\it\tau}=-\int _{V}{\bf\xi}^{\ast }\boldsymbol{\cdot }\boldsymbol{F}({\bf\xi})\,\text{d}{\it\tau}={\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi}),\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}^{2}\int _{V}{\it\rho}|{\bf\xi}|^{2}\,\text{d}{\it\tau}=-\int _{V}{\bf\xi}^{\ast }\boldsymbol{\cdot }\boldsymbol{F}({\bf\xi})\,\text{d}{\it\tau}={\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi}),\end{eqnarray}$$
where
 $$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})=\int _{V}\text{d}{\it\tau}\,\{|\boldsymbol{Q}|^{2}-{\bf\xi}_{\bot }^{\ast }\boldsymbol{\cdot }\,\boldsymbol{j}\times \boldsymbol{Q}+{\it\gamma}p|\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}|^{2}+({\bf\xi}_{\bot }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}_{\bot }^{\ast }\}\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})=\int _{V}\text{d}{\it\tau}\,\{|\boldsymbol{Q}|^{2}-{\bf\xi}_{\bot }^{\ast }\boldsymbol{\cdot }\,\boldsymbol{j}\times \boldsymbol{Q}+{\it\gamma}p|\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}|^{2}+({\bf\xi}_{\bot }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}_{\bot }^{\ast }\}\end{eqnarray}$$
and
 $$\begin{eqnarray}\boldsymbol{Q}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}\times \boldsymbol{B}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Q}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}\times \boldsymbol{B}).\end{eqnarray}$$
The functional
 ${\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})$
is clearly the change in potential energy due to the perturbation
${\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})$
is clearly the change in potential energy due to the perturbation
![]() ${\bf\xi}$
. If it is positive for all
${\bf\xi}$
. If it is positive for all
![]() ${\bf\xi}$
, then
${\bf\xi}$
, then
![]() ${\it\omega}$
is real and the plasma is stable against all displacements
${\it\omega}$
is real and the plasma is stable against all displacements
![]() ${\bf\xi}$
.
${\bf\xi}$
.
This form of energy principle is the classic one introduced by Bernstein et al. (Reference Bernstein, Frieman, Kruskal and Kulsrud1958). It will later form the starting point for the extensive analysis of ballooning modes (see § 24). But, of course, it is not applicable to mirror machines – since these always involve anisotropic pressure.
An energy principle for plasmas with anisotropic pressure was also given by Bernstein et al. (Reference Bernstein, Frieman, Kruskal and Kulsrud1958), namely
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{2} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+\frac{5}{3}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}+(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot })\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{3}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-3q)^{2}+q\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[{\bf\xi}(p_{\Vert }-p_{\bot })]\nonumber\\ \displaystyle & & \displaystyle \left.-\,(p_{\Vert }-p_{\bot })[\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}+\boldsymbol{a}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-4q^{2}]\vphantom{\frac{5}{3}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{2} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+\frac{5}{3}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}+(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot })\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{3}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-3q)^{2}+q\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }[{\bf\xi}(p_{\Vert }-p_{\bot })]\nonumber\\ \displaystyle & & \displaystyle \left.-\,(p_{\Vert }-p_{\bot })[\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}+\boldsymbol{a}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-4q^{2}]\vphantom{\frac{5}{3}}\right\},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & q=\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & q=\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{a}=(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{n}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{a}=(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{n}. & \displaystyle\end{eqnarray}$$
Unfortunately, even
![]() ${\it\delta}W_{2}$
is not appropriate for plasmas confined by mirrors, as it assumes
there is no heat flow along the field. An energy principle that overcomes this
limitation was given by Kruskal & Oberman (Reference Kruskal and Oberman1958). This is derived somewhat differently from the principles discussed
above. It starts from the plasma energy in the small-Larmor-radius limit,
${\it\delta}W_{2}$
is not appropriate for plasmas confined by mirrors, as it assumes
there is no heat flow along the field. An energy principle that overcomes this
limitation was given by Kruskal & Oberman (Reference Kruskal and Oberman1958). This is derived somewhat differently from the principles discussed
above. It starts from the plasma energy in the small-Larmor-radius limit,
 $$\begin{eqnarray}{\mathcal{E}}=\int _{V}\frac{1}{2}(|\boldsymbol{B}|^{2}+|\boldsymbol{E}|^{2})\,\text{d}{\it\tau}+\mathop{\sum }_{s}\int _{V}\iint \left[\left({\it\epsilon}+\frac{1}{2}v_{E}^{2}\right)m_{s}\,f({\it\epsilon},{\it\mu},\boldsymbol{x})\right]\frac{B}{v_{\Vert }}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\;\text{d}{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}=\int _{V}\frac{1}{2}(|\boldsymbol{B}|^{2}+|\boldsymbol{E}|^{2})\,\text{d}{\it\tau}+\mathop{\sum }_{s}\int _{V}\iint \left[\left({\it\epsilon}+\frac{1}{2}v_{E}^{2}\right)m_{s}\,f({\it\epsilon},{\it\mu},\boldsymbol{x})\right]\frac{B}{v_{\Vert }}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\;\text{d}{\it\tau},\end{eqnarray}$$
(here
 ${\it\mu}=v_{\bot }^{2}/2B$
and
${\it\mu}=v_{\bot }^{2}/2B$
and
 $v_{\Vert }=\sqrt{2({\it\epsilon}-{\it\mu}B)}\,$
). Any perturbation of this energy will contain a part dependent on the
perturbed magnetic field and a part dependent on the perturbed particle distribution.
However, because the guiding centre drift
$v_{\Vert }=\sqrt{2({\it\epsilon}-{\it\mu}B)}\,$
). Any perturbation of this energy will contain a part dependent on the
perturbed magnetic field and a part dependent on the perturbed particle distribution.
However, because the guiding centre drift
![]() $v_{E}$
is the
$v_{E}$
is the
![]() $E\times B$
velocity, we can introduce a displacement
$E\times B$
velocity, we can introduce a displacement
![]() ${\bf\xi}$
that links particle motion to changes in the magnetic field (the
frozen-in field condition, see § 4.1). Then,
holding
${\bf\xi}$
that links particle motion to changes in the magnetic field (the
frozen-in field condition, see § 4.1). Then,
holding
![]() ${\bf\xi}$
fixed and minimising over the particle distribution gives a form
${\bf\xi}$
fixed and minimising over the particle distribution gives a form
![]() ${\it\delta}W_{3}$
that depends (after some algebra; see Kruskal & Oberman Reference Kruskal and Oberman1958; Taylor & Hastie Reference Taylor and Hastie1965) only on the displacement
${\it\delta}W_{3}$
that depends (after some algebra; see Kruskal & Oberman Reference Kruskal and Oberman1958; Taylor & Hastie Reference Taylor and Hastie1965) only on the displacement
![]() ${\bf\xi}$
and equilibrium quantities
${\bf\xi}$
and equilibrium quantities
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+(2p_{\bot }+C)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\,{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)+({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\Vert })q\nonumber\\ \displaystyle & & \displaystyle -\,(p_{\Vert }-p_{\bot })[\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}+\boldsymbol{a}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-q^{2}-q\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}]\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\langle v_{\Vert }^{2}q+{\it\mu}B(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+(2p_{\bot }+C)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\,{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)+({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\Vert })q\nonumber\\ \displaystyle & & \displaystyle -\,(p_{\Vert }-p_{\bot })[\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}+\boldsymbol{a}\boldsymbol{\cdot }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}){\bf\xi}-q^{2}-q\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}]\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\langle v_{\Vert }^{2}q+{\it\mu}B(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-q)\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\},\end{eqnarray}$$
where the average in the last term is defined as
 $$\begin{eqnarray}\langle g\rangle =\left(\int g\frac{\text{d}l}{v_{\Vert }}\right)\left(\int \frac{\text{d}l}{v_{\Vert }}\right)^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\langle g\rangle =\left(\int g\frac{\text{d}l}{v_{\Vert }}\right)\left(\int \frac{\text{d}l}{v_{\Vert }}\right)^{-1}\end{eqnarray}$$
and
 $$\begin{eqnarray}C=\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}({\it\mu}B)^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}.\end{eqnarray}$$
$$\begin{eqnarray}C=\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}({\it\mu}B)^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}.\end{eqnarray}$$
19.1. Application to special minimum-
 $B$
equilibria
$B$
equilibria
For the special equilibria introduced in § 18.3,
 $p_{\Vert }=p_{\Vert }(B)$
,
$p_{\Vert }=p_{\Vert }(B)$
,
 $p_{\bot }=p_{\bot }(B)$
and
$p_{\bot }=p_{\bot }(B)$
and
 $$\begin{eqnarray}Bp_{\Vert }^{\prime }=p_{\Vert }-p_{\bot },\quad Bp_{\bot }^{\prime }=2p_{\bot }+C,\quad j_{\Vert }=0,\end{eqnarray}$$
$$\begin{eqnarray}Bp_{\Vert }^{\prime }=p_{\Vert }-p_{\bot },\quad Bp_{\bot }^{\prime }=2p_{\bot }+C,\quad j_{\Vert }=0,\end{eqnarray}$$
where the vanishing of
![]() $j_{\Vert }$
follows from (18.7). A more convenient form of
$j_{\Vert }$
follows from (18.7). A more convenient form of
![]() ${\it\delta}W_{3}$
is then (Taylor & Hastie Reference Taylor and Hastie1965)
${\it\delta}W_{3}$
is then (Taylor & Hastie Reference Taylor and Hastie1965)
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}_{\bot }|^{2}\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+Q_{\Vert }^{2}\left(1+\frac{2p_{\bot }+C}{B^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\,j_{\Vert }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}_{\bot })\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+q[{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\Vert }+(p_{\bot }-p_{\Vert })s]\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left(2\frac{Q_{\Vert }}{B}+s\right)[{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }-(2p_{\bot }+C)s]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\left\langle v_{\Vert }^{2}q-{\it\mu}B\left(\frac{Q_{\Vert }}{B}+s\right)\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}_{\bot }|^{2}\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+Q_{\Vert }^{2}\left(1+\frac{2p_{\bot }+C}{B^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\,j_{\Vert }(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}_{\bot })\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+q[{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\Vert }+(p_{\bot }-p_{\Vert })s]\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left(2\frac{Q_{\Vert }}{B}+s\right)[{\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }-(2p_{\bot }+C)s]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\left\langle v_{\Vert }^{2}q-{\it\mu}B\left(\frac{Q_{\Vert }}{B}+s\right)\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\},\end{eqnarray}$$
where
 $s={\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B/B$
. Using (19.16)
this reduces to
$s={\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}B/B$
. Using (19.16)
this reduces to
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}_{\bot }|^{2}\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+Q_{\Vert }^{2}\left(1+\frac{2p_{\bot }+C}{B^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\left\langle v_{\Vert }^{2}q-{\it\mu}B\left(\frac{Q_{\Vert }}{B}+s\right)\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{3} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}|\boldsymbol{Q}_{\bot }|^{2}\left(1+\frac{p_{\bot }-p_{\Vert }}{B^{2}}\right)+Q_{\Vert }^{2}\left(1+\frac{2p_{\bot }+C}{B^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}\left\langle v_{\Vert }^{2}q-{\it\mu}B\left(\frac{Q_{\Vert }}{B}+s\right)\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
Therefore, sufficient conditions for stability of the special equilibria are
 $$\begin{eqnarray}B^{2}-p_{\Vert }+p_{\bot }>0,\quad B^{2}+2p_{\bot }+C>0,\end{eqnarray}$$
$$\begin{eqnarray}B^{2}-p_{\Vert }+p_{\bot }>0,\quad B^{2}+2p_{\bot }+C>0,\end{eqnarray}$$
which, using (19.16), can be expressed in terms of the pressure gradients as
 $$\begin{eqnarray}B-\frac{\text{d}p_{\Vert }}{\text{d}B}>0,\quad B+\frac{\text{d}p_{\bot }}{\text{d}B}>0.\end{eqnarray}$$
$$\begin{eqnarray}B-\frac{\text{d}p_{\Vert }}{\text{d}B}>0,\quad B+\frac{\text{d}p_{\bot }}{\text{d}B}>0.\end{eqnarray}$$
The first of these is usually satisfied for plasma contained in a
magnetic well as the pressure falls and
![]() $B$
increases towards the boundary, i.e.
$B$
increases towards the boundary, i.e.
 $\text{d}p_{\Vert }/\text{d}B<0$
. By integrating the second inequality from the ‘bottom’ of the well
to the plasma boundary, which is a contour of constant
$\text{d}p_{\Vert }/\text{d}B<0$
. By integrating the second inequality from the ‘bottom’ of the well
to the plasma boundary, which is a contour of constant
![]() $|\boldsymbol{B}|$
, we find that the maximum stable pressure is equal to the ‘depth’
of the well,
$|\boldsymbol{B}|$
, we find that the maximum stable pressure is equal to the ‘depth’
of the well,
 $$\begin{eqnarray}p_{\bot ,max}=(B_{b}^{2}-B_{c}^{2})/2,\end{eqnarray}$$
$$\begin{eqnarray}p_{\bot ,max}=(B_{b}^{2}-B_{c}^{2})/2,\end{eqnarray}$$
where
![]() $B_{b}$
is the field on the plasma boundary, and
$B_{b}$
is the field on the plasma boundary, and
![]() $B_{c}$
is the field at the ‘bottom’ of the well.
$B_{c}$
is the field at the ‘bottom’ of the well.
We see therefore that the special equilibria in magnetic wells are not only remarkable, in that they can be described without knowledge of the field geometry, but they also have remarkably simple and robust stability properties.
Before we discuss the stability of general equilibria in magnetic wells, which we
hope will inherit some of the desirable features of the special equilibria, it is
interesting to note a proof of stability that does not require the elaborate
structure of the energy principles – although it is applicable only at low
![]() ${\it\beta}$
.
${\it\beta}$
.
19.2. Direct proof of stability for special equilibria at low
 ${\it\beta}$
${\it\beta}$
As long as the motion is conservative, we know from Liouville’s theorem that the
density of particles in phase space remains constant as one moves with the particles.
If the particles also carry with them a constant quantity
![]() ${\it\mu}$
(the magnetic moment), then we can construct a constant of motion
${\it\mu}$
(the magnetic moment), then we can construct a constant of motion
![]() $G(\,f,{\it\mu})$
such that (Taylor Reference Taylor1963)
$G(\,f,{\it\mu})$
such that (Taylor Reference Taylor1963)
 $$\begin{eqnarray}{\mathcal{S}}=\int G(\,f,{\it\mu})\,\text{d}^{3}v\;\text{d}^{3}x=\text{constant}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}=\int G(\,f,{\it\mu})\,\text{d}^{3}v\;\text{d}^{3}x=\text{constant}\end{eqnarray}$$
or
 $$\begin{eqnarray}\int \frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}G(\,f,{\it\mu})\,\text{d}{\it\epsilon}\,\text{d}{\it\mu}\,\text{d}^{3}x=\text{constant}.\end{eqnarray}$$
$$\begin{eqnarray}\int \frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}G(\,f,{\it\mu})\,\text{d}{\it\epsilon}\,\text{d}{\it\mu}\,\text{d}^{3}x=\text{constant}.\end{eqnarray}$$
Now consider a perturbation of
![]() $f$
around its initial value
$f$
around its initial value
![]() $f_{0}$
. Then
$f_{0}$
. Then
 $$\begin{eqnarray}{\it\delta}{\mathcal{S}}=0=\int \left[G^{\prime }(\,f_{0},{\it\mu})\,{\it\delta}f+G^{\prime \prime }(\,f_{0},{\it\mu})\frac{({\it\delta}f)^{2}}{2}+\cdots \right]\text{d}^{3}v\,\text{d}^{3}x,\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}{\mathcal{S}}=0=\int \left[G^{\prime }(\,f_{0},{\it\mu})\,{\it\delta}f+G^{\prime \prime }(\,f_{0},{\it\mu})\frac{({\it\delta}f)^{2}}{2}+\cdots \right]\text{d}^{3}v\,\text{d}^{3}x,\end{eqnarray}$$
where the prime denotes the derivative with respect to
![]() $f$
.
$f$
.
The special equilibria have the property that
![]() $f_{0}$
is a function only of
$f_{0}$
is a function only of
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() ${\it\epsilon}$
, so if
${\it\epsilon}$
, so if
![]() $f_{0}({\it\mu},{\it\epsilon})$
is monotonic in
$f_{0}({\it\mu},{\it\epsilon})$
is monotonic in
![]() ${\it\epsilon}$
, we can choose the function
${\it\epsilon}$
, we can choose the function
![]() $G$
such that,
$G$
such that,
 $$\begin{eqnarray}G^{\prime }(\,f_{0},{\it\mu})={\it\epsilon},\quad G^{\prime \prime }(\,f_{0},{\it\mu})=\left(\frac{\partial f_{0}}{\partial {\it\epsilon}}\right)^{-1},\end{eqnarray}$$
$$\begin{eqnarray}G^{\prime }(\,f_{0},{\it\mu})={\it\epsilon},\quad G^{\prime \prime }(\,f_{0},{\it\mu})=\left(\frac{\partial f_{0}}{\partial {\it\epsilon}}\right)^{-1},\end{eqnarray}$$
for all
![]() ${\it\mu}$
. Then when
${\it\mu}$
. Then when
![]() $f$
is small,
$f$
is small,
 $$\begin{eqnarray}\int {\it\epsilon}{\it\delta}f\,\text{d}^{3}v\,\text{d}^{3}x\sim -\!\int \frac{({\it\delta}f)^{2}}{2\partial f_{0}/\partial {\it\epsilon}}\frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\text{d}^{3}x.\end{eqnarray}$$
$$\begin{eqnarray}\int {\it\epsilon}{\it\delta}f\,\text{d}^{3}v\,\text{d}^{3}x\sim -\!\int \frac{({\it\delta}f)^{2}}{2\partial f_{0}/\partial {\it\epsilon}}\frac{B}{({\it\epsilon}-{\it\mu}B)^{1/2}}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\,\text{d}^{3}x.\end{eqnarray}$$
The left-hand side of this equation is the change in energy of the
particles, and the right-hand side is positive definite. Hence any perturbation
increases the kinetic energy of the particles. Also, at low
![]() ${\it\beta}$
any change in magnetic field increases its energy. Consequently,
the system is stable. In fact, this suggests that at low
${\it\beta}$
any change in magnetic field increases its energy. Consequently,
the system is stable. In fact, this suggests that at low
![]() ${\it\beta}$
the special minimum-
${\it\beta}$
the special minimum-
![]() $B$
equilibria, irrespective of their geometrical shape, are stable to
any perturbation that does not affect the magnetic moment!
$B$
equilibria, irrespective of their geometrical shape, are stable to
any perturbation that does not affect the magnetic moment!
20. Canonical description of guiding centre motion
In practice, it would be extremely difficult to produce the special equilibria, so we must now turn to more general equilibria in magnetic wells. For this, it is convenient to introduce a description in terms of the average guiding centre drifts (Taylor Reference Taylor1965, Reference Taylor1968).
We know that the instantaneous guiding centre drift of a particle with charge
![]() $q$
(see § 1.3) is
$q$
(see § 1.3) is
 $$\begin{eqnarray}\boldsymbol{v}_{B}=\frac{1}{q}\,\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{3}}(2{\it\epsilon}-{\it\mu}B),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{B}=\frac{1}{q}\,\frac{\boldsymbol{B}\times \boldsymbol{{\rm\nabla}}B}{B^{3}}(2{\it\epsilon}-{\it\mu}B),\end{eqnarray}$$
but in view of the rapid motion along lines of force, the instantaneous drift is less significant than the average drift over a ‘bounce’ period between mirrors. This average drift can be described in a particularly elegant way.
We first take the field lines themselves as our coordinate system, setting (see § 2.1)
 $$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta},\quad {\it\chi}=\int \boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{l},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\alpha}\times \boldsymbol{{\rm\nabla}}{\it\beta},\quad {\it\chi}=\int \boldsymbol{B}\boldsymbol{\cdot }\text{d}\boldsymbol{l},\end{eqnarray}$$
where
![]() $\text{d}\boldsymbol{l}$
follows a field line. Then
$\text{d}\boldsymbol{l}$
follows a field line. Then
 $({\it\alpha},{\it\beta},{\it\chi})$
locate any point in space, and in these coordinates the instantaneous
drift in (say) the
$({\it\alpha},{\it\beta},{\it\chi})$
locate any point in space, and in these coordinates the instantaneous
drift in (say) the
![]() ${\it\alpha}$
direction is
${\it\alpha}$
direction is
 $$\begin{eqnarray}\frac{\text{d}{\it\alpha}}{\text{d}t}=\boldsymbol{v}_{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha}=-\frac{1}{qB}(2{\it\epsilon}-{\it\mu}B)\left(\frac{\partial B}{\partial {\it\beta}}\right)_{\!{\it\alpha}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}{\it\alpha}}{\text{d}t}=\boldsymbol{v}_{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\alpha}=-\frac{1}{qB}(2{\it\epsilon}-{\it\mu}B)\left(\frac{\partial B}{\partial {\it\beta}}\right)_{\!{\it\alpha}}.\end{eqnarray}$$
If we now introduce the energy
 $K({\it\alpha},{\it\beta},{\it\mu},J)$
defined by
$K({\it\alpha},{\it\beta},{\it\mu},J)$
defined by
 $$\begin{eqnarray}J=\oint _{{\it\alpha}{\it\beta}}(K-{\it\mu}B)^{1/2}\,\frac{\text{d}{\it\chi}}{B},\end{eqnarray}$$
$$\begin{eqnarray}J=\oint _{{\it\alpha}{\it\beta}}(K-{\it\mu}B)^{1/2}\,\frac{\text{d}{\it\chi}}{B},\end{eqnarray}$$
then by direct differentiation
 $$\begin{eqnarray}\left(\frac{\partial K}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}}=\left[\oint \frac{(2K-{\it\mu}B)}{B(K-{\it\mu}B)^{1/2}}\,\frac{\text{d}{\it\chi}}{B}\right]\left[\oint \frac{1}{(K-{\it\mu}B)^{1/2}}\,\frac{\text{d}{\it\chi}}{B}\right]^{-1}\left(\frac{\partial B}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{\partial K}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}}=\left[\oint \frac{(2K-{\it\mu}B)}{B(K-{\it\mu}B)^{1/2}}\,\frac{\text{d}{\it\chi}}{B}\right]\left[\oint \frac{1}{(K-{\it\mu}B)^{1/2}}\,\frac{\text{d}{\it\chi}}{B}\right]^{-1}\left(\frac{\partial B}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}}.\end{eqnarray}$$
The right-hand side of (20.5) is just the average guiding centre drift in the
![]() ${\it\alpha}$
direction, so the equation of motion for this average drift is
${\it\alpha}$
direction, so the equation of motion for this average drift is
 $$\begin{eqnarray}q\left\langle \frac{\text{d}{\it\alpha}}{\text{d}t}\right\rangle =-\left(\frac{\partial K}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}},\end{eqnarray}$$
$$\begin{eqnarray}q\left\langle \frac{\text{d}{\it\alpha}}{\text{d}t}\right\rangle =-\left(\frac{\partial K}{\partial {\it\beta}}\right)_{\!{\it\alpha},J,{\it\mu}},\end{eqnarray}$$
and in a similar way
 $$\begin{eqnarray}q\left\langle \frac{\text{d}{\it\beta}}{\text{d}t}\right\rangle =\left(\frac{\partial K}{\partial {\it\alpha}}\right)_{\!{\it\beta},J,{\it\mu}}.\end{eqnarray}$$
$$\begin{eqnarray}q\left\langle \frac{\text{d}{\it\beta}}{\text{d}t}\right\rangle =\left(\frac{\partial K}{\partial {\it\alpha}}\right)_{\!{\it\beta},J,{\it\mu}}.\end{eqnarray}$$
These are just the Hamiltonian equations of motion for the average
drift, with
![]() ${\it\alpha},{\it\beta}$
as conjugate coordinates and
${\it\alpha},{\it\beta}$
as conjugate coordinates and
 $K({\it\alpha},{\it\beta},{\it\mu},J)$
as the Hamiltonian.
$K({\it\alpha},{\it\beta},{\it\mu},J)$
as the Hamiltonian.
This result is no coincidence! A guiding centre moves as if it were a ‘particle’ that
has a charge
![]() $q$
and magnetic moment
$q$
and magnetic moment
![]() ${\it\mu}$
. The Lagrangian for such a particle is
${\it\mu}$
. The Lagrangian for such a particle is
 $$\begin{eqnarray}{\mathcal{L}}={\textstyle \frac{1}{2}}mv^{2}+q(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{A})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}={\textstyle \frac{1}{2}}mv^{2}+q(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{A})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}).\end{eqnarray}$$
If we take the vector potential as
 $\boldsymbol{A}=({\it\alpha}\boldsymbol{{\rm\nabla}}{\it\beta}-{\it\beta}\boldsymbol{{\rm\nabla}}{\it\alpha})/2$
, so that
$\boldsymbol{A}=({\it\alpha}\boldsymbol{{\rm\nabla}}{\it\beta}-{\it\beta}\boldsymbol{{\rm\nabla}}{\it\alpha})/2$
, so that
 $\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{A}=({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})/2$
, then the guiding centre Lagrangian becomes
$\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{A}=({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})/2$
, then the guiding centre Lagrangian becomes
 $$\begin{eqnarray}{\mathcal{L}}=\frac{1}{2}mv_{d}^{2}+\frac{m\dot{{\it\chi}}^{2}}{2B^{2}}+\frac{q}{2}({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}=\frac{1}{2}mv_{d}^{2}+\frac{m\dot{{\it\chi}}^{2}}{2B^{2}}+\frac{q}{2}({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}),\end{eqnarray}$$
where
![]() $mv_{d}^{2}$
is the energy associated with the slow transverse drift and is
negligible compared to the energy of the parallel motion. Neglecting this drift energy,
$mv_{d}^{2}$
is the energy associated with the slow transverse drift and is
negligible compared to the energy of the parallel motion. Neglecting this drift energy,
 $$\begin{eqnarray}{\mathcal{L}}=\frac{m\dot{{\it\chi}}^{2}}{2B^{2}}+\frac{q}{2}({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}=\frac{m\dot{{\it\chi}}^{2}}{2B^{2}}+\frac{q}{2}({\it\alpha}\dot{{\it\beta}}-{\it\beta}\dot{{\it\alpha}})-q\,{\it\phi}({\it\alpha},{\it\beta},{\it\chi})-{\it\mu}B({\it\alpha},{\it\beta},{\it\chi}),\end{eqnarray}$$
and we see immediately that
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
are indeed conjugate Hamiltonian coordinates,
${\it\beta}$
are indeed conjugate Hamiltonian coordinates,
 $$\begin{eqnarray}p_{{\it\beta}}=\frac{\partial {\mathcal{L}}}{\partial \dot{{\it\beta}}}=\frac{q{\it\alpha}}{2},\quad p_{{\it\alpha}}=\frac{\partial {\mathcal{L}}}{\partial \dot{{\it\alpha}}}=-\frac{q{\it\beta}}{2}.\end{eqnarray}$$
$$\begin{eqnarray}p_{{\it\beta}}=\frac{\partial {\mathcal{L}}}{\partial \dot{{\it\beta}}}=\frac{q{\it\alpha}}{2},\quad p_{{\it\alpha}}=\frac{\partial {\mathcal{L}}}{\partial \dot{{\it\alpha}}}=-\frac{q{\it\beta}}{2}.\end{eqnarray}$$
21. General equilibria in mirror machines
Now that we have the simple forms (20.6) and (20.7) for the
average drift motion, we can immediately describe equilibria in a mirror machine (Taylor
Reference Taylor1964). If the number of particles with
invariants (
![]() ${\it\mu},J$
) in a flux tube of cross-section
${\it\mu},J$
) in a flux tube of cross-section
![]() $\text{d}{\it\alpha}\,\text{d}{\it\beta}$
is
$\text{d}{\it\alpha}\,\text{d}{\it\beta}$
is
 $F({\it\alpha},{\it\beta},{\it\mu},J,t)$
then
$F({\it\alpha},{\it\beta},{\it\mu},J,t)$
then
 $$\begin{eqnarray}\frac{\partial F}{\partial t}+\left\langle \frac{\text{d}{\it\alpha}}{\text{d}t}\right\rangle \frac{\partial F}{\partial {\it\alpha}}+\left\langle \frac{\text{d}{\it\beta}}{\text{d}t}\right\rangle \frac{\partial F}{\partial {\it\beta}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial F}{\partial t}+\left\langle \frac{\text{d}{\it\alpha}}{\text{d}t}\right\rangle \frac{\partial F}{\partial {\it\alpha}}+\left\langle \frac{\text{d}{\it\beta}}{\text{d}t}\right\rangle \frac{\partial F}{\partial {\it\beta}}=0,\end{eqnarray}$$
 $$\begin{eqnarray}\frac{\partial F}{\partial t}-\frac{\partial K}{\partial {\it\beta}}\frac{\partial F}{\partial {\it\alpha}}+\frac{\partial K}{\partial {\it\alpha}}\frac{\partial F}{\partial {\it\beta}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial F}{\partial t}-\frac{\partial K}{\partial {\it\beta}}\frac{\partial F}{\partial {\it\alpha}}+\frac{\partial K}{\partial {\it\alpha}}\frac{\partial F}{\partial {\it\beta}}=0.\end{eqnarray}$$
In equilibrium,
 $\partial F/\partial t=0$
, so
$\partial F/\partial t=0$
, so
![]() $F$
must depend on
$F$
must depend on
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
only through
${\it\beta}$
only through
 $K({\it\alpha},{\it\beta},{\it\mu},J)$
, i.e.
$K({\it\alpha},{\it\beta},{\it\mu},J)$
, i.e.
 $$\begin{eqnarray}F_{eq}({\it\alpha},{\it\beta},{\it\mu},J)=F\{{\it\mu},J,K({\it\alpha},{\it\beta},{\it\mu},J)\}.\end{eqnarray}$$
$$\begin{eqnarray}F_{eq}({\it\alpha},{\it\beta},{\it\mu},J)=F\{{\it\mu},J,K({\it\alpha},{\it\beta},{\it\mu},J)\}.\end{eqnarray}$$
Of course, this just says that
![]() $F$
is a function of the constants of motion. More usefully, it means that
in the (
$F$
is a function of the constants of motion. More usefully, it means that
in the (
![]() ${\it\alpha},{\it\beta}$
) coordinate plane,
${\it\alpha},{\it\beta}$
) coordinate plane,
![]() $F$
is constant on the surfaces
$F$
is constant on the surfaces
 $K=\text{constant}$
.
$K=\text{constant}$
.
21.1. Stability of general equilibria in mirror machines at low
 ${\it\beta}$
${\it\beta}$
At low
![]() ${\it\beta}$
, the most dangerous form of instability is the interchange of flux
tubes, because, if the tubes contain equal flux, there is no increase in magnetic
energy – as there would be for any other perturbation. (In an interchange all the
particles in one flux tube are exchanged with those on a neighbouring flux tube as
the result of
${\it\beta}$
, the most dangerous form of instability is the interchange of flux
tubes, because, if the tubes contain equal flux, there is no increase in magnetic
energy – as there would be for any other perturbation. (In an interchange all the
particles in one flux tube are exchanged with those on a neighbouring flux tube as
the result of
![]() $E\times B$
motion, e.g. as if a circular cross-section tube rotated so that
each semicircular half is replaced by the other.)
$E\times B$
motion, e.g. as if a circular cross-section tube rotated so that
each semicircular half is replaced by the other.)

Figure 54. Numerical calculation of the constant
![]() $K/{\it\mu}$
contours in a minimum-
$K/{\it\mu}$
contours in a minimum-
![]() $B$
system, for
$B$
system, for
 $J/{\it\mu}^{1/2}=0.305$
(from Taylor Reference Taylor1964).
$J/{\it\mu}^{1/2}=0.305$
(from Taylor Reference Taylor1964).
Consider the interchange of a flux tube (1) with a neighbouring tube (2) (Taylor Reference Taylor1964). Before interchange, the total energy of the particles is
 $$\begin{eqnarray}W_{init}=\int (F(1)K(1)+F(2)K(2))\,\text{d}{\it\mu}\,\text{d}J,\end{eqnarray}$$
$$\begin{eqnarray}W_{init}=\int (F(1)K(1)+F(2)K(2))\,\text{d}{\it\mu}\,\text{d}J,\end{eqnarray}$$
where
 $K(1)=K({\it\mu},J,{\it\alpha}_{1},{\it\beta}_{1})$
and
$K(1)=K({\it\mu},J,{\it\alpha}_{1},{\it\beta}_{1})$
and
 $F(1)=F({\it\mu},J,K({\it\mu},J,{\it\alpha}_{1},{\it\beta}_{1}))$
etc.
$F(1)=F({\it\mu},J,K({\it\mu},J,{\it\alpha}_{1},{\it\beta}_{1}))$
etc.
After interchange, the particles
![]() $F(1)$
occupy flux tube
$F(1)$
occupy flux tube
![]() $(2)$
and vice versa, so the total energy is then
$(2)$
and vice versa, so the total energy is then
 $$\begin{eqnarray}W_{final}=\int (F(1)K(2)+F(2)K(1))\,\text{d}{\it\mu}\,\text{d}J.\end{eqnarray}$$
$$\begin{eqnarray}W_{final}=\int (F(1)K(2)+F(2)K(1))\,\text{d}{\it\mu}\,\text{d}J.\end{eqnarray}$$
The change in total energy is therefore
 $$\begin{eqnarray}{\rm\Delta}W=-\int \text{d}{\it\mu}\,\text{d}J\;(F(2)-F(1))(K(2)-K(1)),\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}W=-\int \text{d}{\it\mu}\,\text{d}J\;(F(2)-F(1))(K(2)-K(1)),\end{eqnarray}$$
and, if the displacements are small,
 $$\begin{eqnarray}{\it\delta}W=-\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial F}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial F}{\partial {\it\beta}}{\it\delta}{\it\beta}\right)\left(\frac{\partial K}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial K}{\partial {\it\beta}}{\it\delta}{\it\beta}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W=-\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial F}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial F}{\partial {\it\beta}}{\it\delta}{\it\beta}\right)\left(\frac{\partial K}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial K}{\partial {\it\beta}}{\it\delta}{\it\beta}\right).\end{eqnarray}$$
As
![]() $F$
depends on
$F$
depends on
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
only through
${\it\beta}$
only through
![]() $K$
,
$K$
,
 $$\begin{eqnarray}{\it\delta}W=-\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial F}{\partial K}\right)_{\!{\it\mu},J}\left(\frac{\partial K}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial K}{\partial {\it\beta}}{\it\delta}{\it\beta}\right)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W=-\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial F}{\partial K}\right)_{\!{\it\mu},J}\left(\frac{\partial K}{\partial {\it\alpha}}{\it\delta}{\it\alpha}+\frac{\partial K}{\partial {\it\beta}}{\it\delta}{\it\beta}\right)^{2}.\end{eqnarray}$$
This is clearly positive if
 $$\begin{eqnarray}\left(\frac{\partial F}{\partial K}\right)_{\!{\it\mu},J}<0,\end{eqnarray}$$
$$\begin{eqnarray}\left(\frac{\partial F}{\partial K}\right)_{\!{\it\mu},J}<0,\end{eqnarray}$$
for all
![]() ${\it\mu},J$
– and this is a sufficient condition for stability. The necessary
and sufficient conditions are:
${\it\mu},J$
– and this is a sufficient condition for stability. The necessary
and sufficient conditions are:
![]() ${\it\lambda}_{{\it\alpha}{\it\alpha}}<0$
,
${\it\lambda}_{{\it\alpha}{\it\alpha}}<0$
,
![]() ${\it\lambda}_{{\it\beta}{\it\beta}}<0$
and
${\it\lambda}_{{\it\beta}{\it\beta}}<0$
and
 $[{\it\lambda}_{{\it\alpha}{\it\beta}}]^{2}>{\it\lambda}_{{\it\alpha}{\it\alpha}}{\it\lambda}_{{\it\beta}{\it\beta}}$
, where
$[{\it\lambda}_{{\it\alpha}{\it\beta}}]^{2}>{\it\lambda}_{{\it\alpha}{\it\alpha}}{\it\lambda}_{{\it\beta}{\it\beta}}$
, where
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\alpha}{\it\alpha}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\alpha}}\right)^{2}\left(\frac{\partial F}{\partial K}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\alpha}{\it\alpha}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\alpha}}\right)^{2}\left(\frac{\partial F}{\partial K}\right), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\beta}{\it\beta}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\beta}}\right)^{2}\left(\frac{\partial F}{\partial K}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\beta}{\it\beta}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\beta}}\right)^{2}\left(\frac{\partial F}{\partial K}\right), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\alpha}{\it\beta}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\alpha}}\right)\left(\frac{\partial K}{\partial {\it\beta}}\right)\left(\frac{\partial F}{\partial K}\right). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}_{{\it\alpha}{\it\beta}}=\int \text{d}{\it\mu}\,\text{d}J\left(\frac{\partial K}{\partial {\it\alpha}}\right)\left(\frac{\partial K}{\partial {\it\beta}}\right)\left(\frac{\partial F}{\partial K}\right). & \displaystyle\end{eqnarray}$$
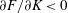 $\partial F/\partial K<0$
and the plasma to be contained (i.e.
$\partial F/\partial K<0$
and the plasma to be contained (i.e.
 $K({\it\alpha},{\it\beta},{\it\mu},J)$
must form a closed nested set surrounding a minimum, in much the
same way that the constant
$K({\it\alpha},{\it\beta},{\it\mu},J)$
must form a closed nested set surrounding a minimum, in much the
same way that the constant
An example of the constant
![]() $K$
contours, calculated for an Ioffe-bar-stabilised mirror (see
figure 51), is shown in figure 54. The figure shows one quadrant of the
cross-section, and the useful confinement region is that inside the last closed
contour enclosing the origin. Note that this calculation exploits the fact that
$K$
contours, calculated for an Ioffe-bar-stabilised mirror (see
figure 51), is shown in figure 54. The figure shows one quadrant of the
cross-section, and the useful confinement region is that inside the last closed
contour enclosing the origin. Note that this calculation exploits the fact that
![]() $K$
is actually a function of only three variables, since
$K$
is actually a function of only three variables, since
 $$\begin{eqnarray}\frac{J}{{\it\mu}^{1/2}}=\oint \left[\frac{K}{{\it\mu}}-B({\it\alpha},{\it\beta},{\it\chi})\right]^{1/2}\frac{\text{d}{\it\chi}}{B},\end{eqnarray}$$
$$\begin{eqnarray}\frac{J}{{\it\mu}^{1/2}}=\oint \left[\frac{K}{{\it\mu}}-B({\it\alpha},{\it\beta},{\it\chi})\right]^{1/2}\frac{\text{d}{\it\chi}}{B},\end{eqnarray}$$
so that
 $K={\it\mu}\hat{K}({\it\alpha},{\it\beta},J/{\it\mu}^{1/2})$
.
$K={\it\mu}\hat{K}({\it\alpha},{\it\beta},J/{\it\mu}^{1/2})$
.
The constant
![]() $K$
contours are analogous to atmospheric isobars. Particles drift
along contours of constant
$K$
contours are analogous to atmospheric isobars. Particles drift
along contours of constant
![]() $K$
just as the wind flows along isobars, and the drift speed increases
as the
$K$
just as the wind flows along isobars, and the drift speed increases
as the
![]() $K$
contours get closer – just as the wind increases as the isobars get
closer.
$K$
contours get closer – just as the wind increases as the isobars get
closer.
22. Maximal ordering and stability
The discussion of general equilibria above is elegant and, within its limits, complete,
but it is unnecessarily detailed for many purposes. Furthermore, as it is restricted to
low
![]() ${\it\beta}$
, it cannot determine the all-important maximum stable
${\it\beta}$
, it cannot determine the all-important maximum stable
![]() ${\it\beta}$
.
${\it\beta}$
.
To find the maximum
![]() ${\it\beta}$
for a general equilibrium, we must fall back on an approximate method.
This is sometimes called ‘maximal ordering’ and is a very important technique – not so
much for its immediate application but because it is used in many plasma problems, in
both mirror and toroidal systems.
${\it\beta}$
for a general equilibrium, we must fall back on an approximate method.
This is sometimes called ‘maximal ordering’ and is a very important technique – not so
much for its immediate application but because it is used in many plasma problems, in
both mirror and toroidal systems.
To illustrate the method, suppose we start from an energy principle and simply expand
![]() ${\it\delta}W$
in powers of
${\it\delta}W$
in powers of
![]() ${\it\beta}$
,
${\it\beta}$
,
 $$\begin{eqnarray}{\it\delta}W={\it\delta}W_{0}+{\it\beta}{\it\delta}W_{1}+{\it\beta}^{2}{\it\delta}W_{2}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W={\it\delta}W_{0}+{\it\beta}{\it\delta}W_{1}+{\it\beta}^{2}{\it\delta}W_{2}+\cdots \,.\end{eqnarray}$$
If we minimised
![]() ${\it\delta}W$
, we might find
${\it\delta}W$
, we might find
 ${\it\delta}W_{0}^{min}=0$
and
${\it\delta}W_{0}^{min}=0$
and
 ${\it\delta}W_{1}^{min}>0$
. Then we would say that at sufficiently small
${\it\delta}W_{1}^{min}>0$
. Then we would say that at sufficiently small
![]() ${\it\beta}$
the plasma is stable, and instability arises only when
${\it\beta}$
the plasma is stable, and instability arises only when
 ${\it\beta}^{2}{\it\delta}W_{2}^{min}$
becomes comparable to
${\it\beta}^{2}{\it\delta}W_{2}^{min}$
becomes comparable to
![]() ${\it\beta}{\it\delta}W_{1}^{min}$
. If so, we could calculate the critical
${\it\beta}{\it\delta}W_{1}^{min}$
. If so, we could calculate the critical
![]() ${\it\beta}$
by evaluating
${\it\beta}$
by evaluating
![]() ${\it\delta}W_{2}^{min}$
and setting
${\it\delta}W_{2}^{min}$
and setting
 ${\it\beta}{\it\delta}W_{1}^{min}=-{\it\beta}^{2}{\it\delta}W_{2}^{min}$
. However, this would be unjustified, because the validity of the
expansion in
${\it\beta}{\it\delta}W_{1}^{min}=-{\it\beta}^{2}{\it\delta}W_{2}^{min}$
. However, this would be unjustified, because the validity of the
expansion in
![]() ${\it\beta}$
is based on the assumption that successive terms get rapidly smaller!
(Strictly we should speak about an asymptotic limit as
${\it\beta}$
is based on the assumption that successive terms get rapidly smaller!
(Strictly we should speak about an asymptotic limit as
![]() ${\it\beta}\rightarrow 0$
, and
${\it\beta}\rightarrow 0$
, and
![]() ${\it\beta}^{2}{\it\delta}W_{2}$
can then never balance
${\it\beta}^{2}{\it\delta}W_{2}$
can then never balance
![]() ${\it\beta}{\it\delta}W_{1}$
!)
${\it\beta}{\it\delta}W_{1}$
!)
To overcome this difficulty, we expand
![]() ${\it\delta}W$
not just in
${\it\delta}W$
not just in
![]() ${\it\beta}$
, but in several small quantities, which are then grouped together so
that they can balance each other. Usually this is done by allocating to
each small quantity a relative order of magnitude in a single small parameter
${\it\beta}$
, but in several small quantities, which are then grouped together so
that they can balance each other. Usually this is done by allocating to
each small quantity a relative order of magnitude in a single small parameter
![]() ${\it\lambda}$
. Then one expands in powers of
${\it\lambda}$
. Then one expands in powers of
![]() ${\it\lambda}$
and stability is determined by the first non-zero term.
Mathematically, this is (hopefully) an asymptotic expansion in
${\it\lambda}$
and stability is determined by the first non-zero term.
Mathematically, this is (hopefully) an asymptotic expansion in
![]() ${\it\lambda}$
. Physically, it is based on the fact that, while
${\it\lambda}$
. Physically, it is based on the fact that, while
![]() ${\it\beta}$
may not be small, some combination of
${\it\beta}$
may not be small, some combination of
![]() ${\it\beta}$
and other quantities is small.
${\it\beta}$
and other quantities is small.
Of course, the key steps are to select the appropriate group of small quantities and to
allocate the appropriate order of magnitude to them. This is something of an art, and it
would be difficult to specify an algorithm. However, the next section shows how these
key steps are dealt with in order to find the maximum stable
![]() ${\it\beta}$
in minimum-
${\it\beta}$
in minimum-
![]() $B$
mirror machines (Taylor Reference Taylor1965;
Taylor & Hastie Reference Taylor and Hastie1965).
$B$
mirror machines (Taylor Reference Taylor1965;
Taylor & Hastie Reference Taylor and Hastie1965).
22.1. Stability of general equilibria in mirror machines at finite
 ${\it\beta}$
${\it\beta}$
In order to apply maximal ordering to minimum-
![]() $B$
confined plasmas, we regard the zero-order (vacuum) magnetic field
as made up of: (i) a uniform field
$B$
confined plasmas, we regard the zero-order (vacuum) magnetic field
as made up of: (i) a uniform field
![]() $\boldsymbol{B}_{0}$
in the
$\boldsymbol{B}_{0}$
in the
![]() $z$
direction, (ii) a mirror component
$z$
direction, (ii) a mirror component
![]() $\boldsymbol{B}_{m}$
approximately parallel to
$\boldsymbol{B}_{m}$
approximately parallel to
![]() $\boldsymbol{B}_{0}$
, and (iii) a stabilising component
$\boldsymbol{B}_{0}$
, and (iii) a stabilising component
![]() $\boldsymbol{B}_{s}$
approximately perpendicular to
$\boldsymbol{B}_{s}$
approximately perpendicular to
![]() $\boldsymbol{B}_{0}$
(as e.g. from Ioffe bars). We also have to include: (iv) the field
$\boldsymbol{B}_{0}$
(as e.g. from Ioffe bars). We also have to include: (iv) the field
![]() $\boldsymbol{B}_{{\it\beta}}$
produced by the plasma currents and (v) the pressure tensor, with
$\boldsymbol{B}_{{\it\beta}}$
produced by the plasma currents and (v) the pressure tensor, with
 $2p_{\bot }/B_{0}^{2}\equiv {\it\beta}_{\bot }$
and
$2p_{\bot }/B_{0}^{2}\equiv {\it\beta}_{\bot }$
and
 $2p_{\Vert }/B_{0}^{2}\equiv {\it\beta}_{\Vert }$
. Therefore, for a shallow magnetic well, we already have five small
quantities:
$2p_{\Vert }/B_{0}^{2}\equiv {\it\beta}_{\Vert }$
. Therefore, for a shallow magnetic well, we already have five small
quantities:
 $$\begin{eqnarray}\frac{B_{m}}{B_{0}}={\it\mu},\quad \frac{B_{s}}{B_{0}}={\it\sigma},\quad \frac{B_{{\it\beta}}}{B_{0}}={\it\beta},\quad \frac{2p_{\bot }}{B_{0}^{2}}={\it\beta}_{\bot },\quad \frac{2p_{\Vert }}{B_{0}^{2}}={\it\beta}_{\Vert }.\end{eqnarray}$$
$$\begin{eqnarray}\frac{B_{m}}{B_{0}}={\it\mu},\quad \frac{B_{s}}{B_{0}}={\it\sigma},\quad \frac{B_{{\it\beta}}}{B_{0}}={\it\beta},\quad \frac{2p_{\bot }}{B_{0}^{2}}={\it\beta}_{\bot },\quad \frac{2p_{\Vert }}{B_{0}^{2}}={\it\beta}_{\Vert }.\end{eqnarray}$$
We want
![]() $B_{m}$
,
$B_{m}$
,
![]() $B_{s}$
and
$B_{s}$
and
![]() $B_{{\it\beta}}$
all to contribute to
$B_{{\it\beta}}$
all to contribute to
![]() $|\boldsymbol{B}|^{2}$
. However,
$|\boldsymbol{B}|^{2}$
. However,
![]() $B_{s}$
is perpendicular to
$B_{s}$
is perpendicular to
![]() $B_{0}$
, so it contributes only quadratically, as
$B_{0}$
, so it contributes only quadratically, as
![]() $B_{s}^{2}$
, and must therefore be of lower order than
$B_{s}^{2}$
, and must therefore be of lower order than
![]() $B_{m}$
or
$B_{m}$
or
![]() $B_{{\it\beta}}$
, which contribute linearly as
$B_{{\it\beta}}$
, which contribute linearly as
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{m}$
and
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{m}$
and
![]() $\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{{\it\beta}}$
. Hence the relative orders must be
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\boldsymbol{B}_{{\it\beta}}$
. Hence the relative orders must be
 $$\begin{eqnarray}\frac{B_{s}}{B_{0}}\sim {\it\lambda},\quad \frac{B_{m}}{B_{0}}\sim {\it\lambda}^{2},\quad \frac{B_{{\it\beta}}}{B_{0}}\sim {\it\lambda}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{B_{s}}{B_{0}}\sim {\it\lambda},\quad \frac{B_{m}}{B_{0}}\sim {\it\lambda}^{2},\quad \frac{B_{{\it\beta}}}{B_{0}}\sim {\it\lambda}^{2}.\end{eqnarray}$$
The relative order of other quantities can be determined from the equilibrium conditions. From the lowest-order equilibrium (see (18.4)),
 $$\begin{eqnarray}\boldsymbol{j}_{\bot }^{{\it\beta}}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{{\it\beta}}=\frac{\boldsymbol{B}_{0}\times \boldsymbol{{\rm\nabla}}p_{\bot }}{B_{0}^{2}},\quad j_{\Vert }=0,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}_{\bot }^{{\it\beta}}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}_{{\it\beta}}=\frac{\boldsymbol{B}_{0}\times \boldsymbol{{\rm\nabla}}p_{\bot }}{B_{0}^{2}},\quad j_{\Vert }=0,\end{eqnarray}$$
we deduce that, since
 $B_{{\it\beta}}/B_{0}\sim {\it\lambda}^{2}$
, we must take
$B_{{\it\beta}}/B_{0}\sim {\it\lambda}^{2}$
, we must take
![]() $j_{\bot }^{{\it\beta}}\sim {\it\lambda}^{2}$
,
$j_{\bot }^{{\it\beta}}\sim {\it\lambda}^{2}$
,
![]() $p_{\bot }\sim {\it\lambda}^{2}$
. The order of
$p_{\bot }\sim {\it\lambda}^{2}$
. The order of
![]() $p_{\Vert }$
can similarly be deduced from the parallel equilibrium as
$p_{\Vert }$
can similarly be deduced from the parallel equilibrium as
![]() $p_{\Vert }\sim {\it\lambda}^{4}$
. So now we have a ‘maximal ordering’,
$p_{\Vert }\sim {\it\lambda}^{4}$
. So now we have a ‘maximal ordering’,
 $$\begin{eqnarray}\frac{B_{s}}{B_{0}}\sim {\it\lambda},\quad \frac{B_{m}}{B_{0}}\sim {\it\lambda}^{2},\quad \frac{B_{{\it\beta}}}{B_{0}}\sim {\it\lambda}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\frac{B_{s}}{B_{0}}\sim {\it\lambda},\quad \frac{B_{m}}{B_{0}}\sim {\it\lambda}^{2},\quad \frac{B_{{\it\beta}}}{B_{0}}\sim {\it\lambda}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}j_{\bot }\sim {\it\lambda}^{2},\quad j_{\Vert }\sim {\it\lambda}^{4},\quad p_{\bot }\sim {\it\lambda}^{2},\quad p_{\Vert }\sim {\it\lambda}^{4}.\end{eqnarray}$$
$$\begin{eqnarray}j_{\bot }\sim {\it\lambda}^{2},\quad j_{\Vert }\sim {\it\lambda}^{4},\quad p_{\bot }\sim {\it\lambda}^{2},\quad p_{\Vert }\sim {\it\lambda}^{4}.\end{eqnarray}$$
However, there are two more steps before the algebra can begin! The displacement,
![]() ${\bf\xi}$
, that minimises
${\bf\xi}$
, that minimises
 ${\it\delta}W({\bf\xi},{\bf\xi})$
will itself depend on
${\it\delta}W({\bf\xi},{\bf\xi})$
will itself depend on
![]() ${\it\lambda}$
, so it too must be expanded,
${\it\lambda}$
, so it too must be expanded,
 $$\begin{eqnarray}{\bf\xi}={\bf\xi}_{0}+{\it\lambda}{\bf\xi}_{1}+{\it\lambda}^{2}{\bf\xi}_{2}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}{\bf\xi}={\bf\xi}_{0}+{\it\lambda}{\bf\xi}_{1}+{\it\lambda}^{2}{\bf\xi}_{2}+\cdots \,,\end{eqnarray}$$
and, before we can expand the Kruskal–Oberman energy functional
(19.17), we must extend the
ordering to include terms depending on the distribution function, rather than the
displacement
![]() ${\bf\xi}$
. From (18.9), the
derivative of
${\bf\xi}$
. From (18.9), the
derivative of
![]() $p_{\bot }$
along the field gives
$p_{\bot }$
along the field gives
 $$\begin{eqnarray}\frac{\partial p_{\bot }}{\partial s}=(C+2p_{\bot })\frac{1}{B}\frac{\partial B}{\partial s},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial p_{\bot }}{\partial s}=(C+2p_{\bot })\frac{1}{B}\frac{\partial B}{\partial s},\end{eqnarray}$$
where
![]() $C$
was given in (19.15). As we have already found both
$C$
was given in (19.15). As we have already found both
![]() $\partial p_{\bot }/\partial s$
and
$\partial p_{\bot }/\partial s$
and
![]() $\partial B/\partial s$
to be of order
$\partial B/\partial s$
to be of order
![]() ${\it\lambda}^{2}$
, we must treat
${\it\lambda}^{2}$
, we must treat
![]() $C$
as a zero-order quantity.
$C$
as a zero-order quantity.
So now, at last, we can expand
 ${\it\delta}W({\bf\xi},{\bf\xi})$
in powers of
${\it\delta}W({\bf\xi},{\bf\xi})$
in powers of
![]() ${\it\lambda}$
. It will be necessary to go to fourth order,
${\it\lambda}$
. It will be necessary to go to fourth order,
![]() ${\it\lambda}^{4}$
, and this involves a lot of algebra.
${\it\lambda}^{4}$
, and this involves a lot of algebra.
In zeroth order, we find
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{0} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}[\boldsymbol{Q}_{\bot 0}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)[Q_{\Vert 0}]^{2}-\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}{\it\mu}^{2}\langle Q_{\Vert 0}\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{0} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{\vphantom{\mathop{\sum }_{s}}[\boldsymbol{Q}_{\bot 0}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)[Q_{\Vert 0}]^{2}-\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}{\it\mu}^{2}\langle Q_{\Vert 0}\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We will assume that
 $\partial f/\partial {\it\epsilon}<0$
throughout, so
$\partial f/\partial {\it\epsilon}<0$
throughout, so
![]() ${\it\delta}W_{0}$
is certainly positive when
${\it\delta}W_{0}$
is certainly positive when
 $$\begin{eqnarray}(1+C/B_{0}^{2})>0.\end{eqnarray}$$
$$\begin{eqnarray}(1+C/B_{0}^{2})>0.\end{eqnarray}$$
However, the minimum
![]() ${\it\delta}W_{0}$
is zero when
${\it\delta}W_{0}$
is zero when
 $\boldsymbol{Q}_{0}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{0}\times \boldsymbol{B}_{0})=0$
, so (22.10) is
only a necessary condition for stability, not a sufficient one, and to determine
sufficient conditions we must proceed to higher order.
$\boldsymbol{Q}_{0}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{0}\times \boldsymbol{B}_{0})=0$
, so (22.10) is
only a necessary condition for stability, not a sufficient one, and to determine
sufficient conditions we must proceed to higher order.
It turns out that
 ${\it\delta}W_{1}\equiv 0$
and
${\it\delta}W_{1}\equiv 0$
and
 $$\begin{eqnarray}{\it\delta}W_{2}=\int _{V}\text{d}{\it\tau}\left\{[\boldsymbol{Q}_{\bot 1}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)[Q_{\Vert 1}]^{2}-\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}{\it\mu}^{2}\langle Q_{\Vert 1}\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W_{2}=\int _{V}\text{d}{\it\tau}\left\{[\boldsymbol{Q}_{\bot 1}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)[Q_{\Vert 1}]^{2}-\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}{\it\mu}^{2}\langle Q_{\Vert 1}\rangle ^{2}\,\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
This is again non-negative, but is zero when
 $$\begin{eqnarray}\boldsymbol{Q}_{1}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{1}\times \boldsymbol{B}_{0})+\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{0}\times \boldsymbol{B}_{s})=0.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Q}_{1}=\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{1}\times \boldsymbol{B}_{0})+\boldsymbol{{\rm\nabla}}\times ({\bf\xi}_{0}\times \boldsymbol{B}_{s})=0.\end{eqnarray}$$
So continuing further,
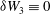 ${\it\delta}W_{3}\equiv 0$
, and finally
${\it\delta}W_{3}\equiv 0$
, and finally
 $$\begin{eqnarray}\displaystyle {\it\delta}W_{4} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{[\boldsymbol{Q}_{\bot 2}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)\left[Q_{\Vert 2}+\frac{Cs_{2}-{\bf\xi}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }}{B_{0}(1+C/B_{0}^{2})}\right]^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{(Cs_{2}-{\bf\xi}_{0}\boldsymbol{{\rm\nabla}}p_{\bot })[{\bf\xi}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(p_{\bot }+B^{2}/2)]}{B^{2}+C}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}({\it\mu}B_{0})^{2}\left\langle \frac{Q_{\Vert 2}}{B}+s_{2}\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W_{4} & = & \displaystyle \int _{V}\text{d}{\it\tau}\left\{[\boldsymbol{Q}_{\bot 2}]^{2}+\left(1+\frac{C}{B_{0}^{2}}\right)\left[Q_{\Vert 2}+\frac{Cs_{2}-{\bf\xi}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{\bot }}{B_{0}(1+C/B_{0}^{2})}\right]^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{(Cs_{2}-{\bf\xi}_{0}\boldsymbol{{\rm\nabla}}p_{\bot })[{\bf\xi}_{0}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(p_{\bot }+B^{2}/2)]}{B^{2}+C}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{s}m_{s}\iint \frac{B_{0}}{v_{\Vert }}\frac{\partial f}{\partial {\it\epsilon}}({\it\mu}B_{0})^{2}\left\langle \frac{Q_{\Vert 2}}{B}+s_{2}\right\rangle ^{2}\text{d}{\it\mu}\,\text{d}{\it\epsilon}\right\}.\end{eqnarray}$$
Several sufficient criteria for stability can be obtained from this last result
(Taylor & Hastie Reference Taylor and Hastie1965). The most useful
and revealing are:
![]() ${\it\delta}W>0$
if
${\it\delta}W>0$
if
 $$\begin{eqnarray}(\boldsymbol{{\rm\nabla}}_{\Vert }B)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\Vert }(p_{\bot }+B^{2}/2)>0\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{{\rm\nabla}}_{\Vert }B)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\Vert }(p_{\bot }+B^{2}/2)>0\end{eqnarray}$$
and
 $$\begin{eqnarray}(\boldsymbol{{\rm\nabla}}_{\bot }B)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\bot }(p_{\bot }+B^{2}/2)>0.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{{\rm\nabla}}_{\bot }B)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\bot }(p_{\bot }+B^{2}/2)>0.\end{eqnarray}$$
From (22.15), the
maximum plasma pressure
![]() $p_{\bot ,max}$
cannot exceed
$p_{\bot ,max}$
cannot exceed
 $(B_{b}^{2}-B_{c}^{2})/2$
, where
$(B_{b}^{2}-B_{c}^{2})/2$
, where
![]() $B_{c}^{2}/2$
is again the magnetic pressure at the minimum of the well but
$B_{c}^{2}/2$
is again the magnetic pressure at the minimum of the well but
![]() $B_{b}^{2}/2$
is now the lowest magnetic pressure on the plasma boundary. (In the
general equilibria, unlike the special ones,
$B_{b}^{2}/2$
is now the lowest magnetic pressure on the plasma boundary. (In the
general equilibria, unlike the special ones,
![]() $B$
is not constant along the plasma boundary.)
$B$
is not constant along the plasma boundary.)
Note that
 $\boldsymbol{{\rm\nabla}}_{\bot }(p_{\bot }+B^{2}/2)$
is related to the curvature of lines of force and the condition
(22.15) is violated when the
diamagnetic plasma currents have so modified the vacuum field that the field
curvature is reversed relative to the zero-
$\boldsymbol{{\rm\nabla}}_{\bot }(p_{\bot }+B^{2}/2)$
is related to the curvature of lines of force and the condition
(22.15) is violated when the
diamagnetic plasma currents have so modified the vacuum field that the field
curvature is reversed relative to the zero-
![]() ${\it\beta}$
situation. When
${\it\beta}$
situation. When
![]() ${\it\beta}$
is small, the lines of force are convex to the plasma (stable
curvature), but, because the plasma is diamagnetic, as the plasma pressure increases,
it causes the lines to ‘bulge out’ and eventually creates unstable curvature.
${\it\beta}$
is small, the lines of force are convex to the plasma (stable
curvature), but, because the plasma is diamagnetic, as the plasma pressure increases,
it causes the lines to ‘bulge out’ and eventually creates unstable curvature.
23. Conclusion
One of the attractions of mirror machines is that one can set up a vacuum mirror field, which is certainly stable, and then introduce plasma gradually. At least at low pressure the plasma should then be well confined – except for the mirror loss cone. (This possibility is not available in toroidal systems such as tokamaks or RFPs, where the plasma itself creates much of the confining field, though it is possible in stellarators.)
Unfortunately, it turns out that plasma in a simple axisymmetric mirror machine is
unstable, even at the lowest pressures. This low-
![]() ${\it\beta}$
instability can be overcome by modifying the field so that there is a
non-zero minimum in
${\it\beta}$
instability can be overcome by modifying the field so that there is a
non-zero minimum in
![]() $B^{2}$
– the ‘minimum-
$B^{2}$
– the ‘minimum-
![]() $B$
’ fields or magnetic wells. However, to do this one must destroy the
symmetry of the field to the extent that it is no longer clear whether the plasma is
even confined!
$B$
’ fields or magnetic wells. However, to do this one must destroy the
symmetry of the field to the extent that it is no longer clear whether the plasma is
even confined!
It is important, therefore, that there is a class of equilibria in magnetic wells that
can be analysed in considerable detail, using both fluid and particle models, without
requiring any knowledge of the actual structure of the magnetic field! This is possible
because in minimum-
![]() $B$
fields the magnetic isobars (surfaces of constant
$B$
fields the magnetic isobars (surfaces of constant
![]() $B^{2}$
) form closed nested surfaces that confine plasmas with
$B^{2}$
) form closed nested surfaces that confine plasmas with
 $p_{\bot }=p_{\bot }(B)$
and
$p_{\bot }=p_{\bot }(B)$
and
 $p_{\Vert }=p_{\Vert }(B)$
.
$p_{\Vert }=p_{\Vert }(B)$
.
These special equilibria are unconditionally stable at low
![]() ${\it\beta}$
in both fluid and particle plasma models. In fact, it appears that the
only requirement for low-
${\it\beta}$
in both fluid and particle plasma models. In fact, it appears that the
only requirement for low-
![]() ${\it\beta}$
stability is that the magnetic moment
${\it\beta}$
stability is that the magnetic moment
 ${\it\mu}=v_{\bot }^{2}/2B$
of all particles should be invariant. The maximum stable pressure
${\it\mu}=v_{\bot }^{2}/2B$
of all particles should be invariant. The maximum stable pressure
![]() $p_{\bot }$
for the special equilibria is equal to the ‘depth’ of the magnetic
well – the difference in
$p_{\bot }$
for the special equilibria is equal to the ‘depth’ of the magnetic
well – the difference in
![]() $B^{2}$
between its minimum and its value on the last closed magnetic
isobar.
$B^{2}$
between its minimum and its value on the last closed magnetic
isobar.
To analyse general equilibria in mirrors, we introduced a Hamiltonian description of the
average (over the bounce motion between mirrors) guiding centre drift. This showed, as
one would expect, that an equilibrium distribution must be a function of the constants
of motion on each field line
 $f=\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
. It also allowed us to calculate the necessary and sufficient
conditions for stability of general low-
$f=\,f({\it\mu},{\it\epsilon},{\it\alpha},{\it\beta})$
. It also allowed us to calculate the necessary and sufficient
conditions for stability of general low-
![]() ${\it\beta}$
equilibria in mirror machines.
${\it\beta}$
equilibria in mirror machines.
We also introduced an important approximate method for calculating the maximum stable
![]() ${\it\beta}$
for general equilibria. This so-called ‘maximal ordering’ is important
in many areas of plasma confinement, in both mirror and toroidal systems. When applied
to mirrors, it showed that for general equilibria the maximum stable
${\it\beta}$
for general equilibria. This so-called ‘maximal ordering’ is important
in many areas of plasma confinement, in both mirror and toroidal systems. When applied
to mirrors, it showed that for general equilibria the maximum stable
![]() ${\it\beta}$
is again related to the ‘depth’ of the magnetic well – in this case
the difference in
${\it\beta}$
is again related to the ‘depth’ of the magnetic well – in this case
the difference in
![]() $B^{2}$
between its minimum and its lowest value on the plasma boundary (which
in general is not a magnetic isobar).
$B^{2}$
between its minimum and its lowest value on the plasma boundary (which
in general is not a magnetic isobar).
However, despite their attraction in terms of control, stability and susceptibility to theoretical analysis, mirror machines suffer from an inevitable loss of plasma due to collisional scattering into the mirror loss cones. Despite heroic attempts to plug these losses by complex multiple mirrors, electrostatic barriers, thermal barriers, radiation barriers, etc., it seems that the loss cannot be reduced to a level acceptable for fusion reactors – the original motivation for studying mirror machines. However, they remain a valuable research tool and are used (in an independent development) as ‘magnetic traps’ for studies of single atoms and Bose–Einstein condensates, etc.
Part IV
24. Ballooning modes
The theory of ballooning modes is one of the most intriguing topics in plasma stability
theory. It represents a significant step forwards from the study of idealised
configurations such as the plane slab and infinite circular cylinder – in which
ballooning modes do not exist – to more realistic toroidal systems with
arbitrary cross-section and arbitrary aspect ratio – in which ballooning modes
are important. They set a maximum
![]() ${\it\beta}$
for plasma stability in a tokamak and fill a gap that previously
existed in the theory of toroidal plasmas.
${\it\beta}$
for plasma stability in a tokamak and fill a gap that previously
existed in the theory of toroidal plasmas.
But before we embark on the investigation of ballooning modes, we should look at the theory of instabilities in an infinite circular cylinder, even though that investigation cannot be extended to toroidal systems.
24.1. Stability of plasma in circular cylinders
A full linear stability analysis can be carried out for plasma in an infinite
circular cylinder. This is possible because any linear perturbation can be reduced to
a sum over independent one-dimensional Fourier modes
 ${\bf\xi}(r)\exp [\text{i}(m{\it\theta}+kz)]$
, as in the classic analysis of Newcomb (Reference Newcomb1960).
${\bf\xi}(r)\exp [\text{i}(m{\it\theta}+kz)]$
, as in the classic analysis of Newcomb (Reference Newcomb1960).
If, following Newcomb, we consider a single Fourier mode
![]() $(m,k)$
and drop the exponential factor, the displacement can be expressed
in terms of the real variables
$(m,k)$
and drop the exponential factor, the displacement can be expressed
in terms of the real variables
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-\frac{1}{r}\frac{\text{d}}{\text{d}r}(r{\it\xi}_{r})=\frac{\text{i}m}{r}{\it\xi}_{{\it\theta}}+\text{i}k{\it\xi}_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}-\frac{1}{r}\frac{\text{d}}{\text{d}r}(r{\it\xi}_{r})=\frac{\text{i}m}{r}{\it\xi}_{{\it\theta}}+\text{i}k{\it\xi}_{z}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\it\zeta}=\text{i}({\bf\xi}\times \boldsymbol{B})_{r}=\text{i}{\it\xi}_{{\it\theta}}B_{z}-\text{i}{\it\xi}_{z}B_{{\it\theta}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\zeta}=\text{i}({\bf\xi}\times \boldsymbol{B})_{r}=\text{i}{\it\xi}_{{\it\theta}}B_{z}-\text{i}{\it\xi}_{z}B_{{\it\theta}}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}{\it\xi}_{{\it\theta}}=-\text{i}\frac{kr{\it\zeta}+rB_{{\it\theta}}{\it\eta}}{krB_{z}+mB_{{\it\theta}}},\quad {\it\xi}_{z}=\text{i}\frac{m{\it\zeta}-rB_{z}{\it\eta}}{krB_{z}+mB_{{\it\theta}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}_{{\it\theta}}=-\text{i}\frac{kr{\it\zeta}+rB_{{\it\theta}}{\it\eta}}{krB_{z}+mB_{{\it\theta}}},\quad {\it\xi}_{z}=\text{i}\frac{m{\it\zeta}-rB_{z}{\it\eta}}{krB_{z}+mB_{{\it\theta}}}.\end{eqnarray}$$
After some algebra, the energy functional for isotropic pressure
![]() ${\it\delta}W_{1}$
(see (19.7)),
${\it\delta}W_{1}$
(see (19.7)),
 $$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})=\frac{1}{2}\int _{V}\text{d}{\it\tau}\;\{|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }{\bf\xi}^{\ast }\times \boldsymbol{Q}+(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}^{\ast }){\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+{\it\gamma}p(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}\},\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi}^{\ast },{\bf\xi})=\frac{1}{2}\int _{V}\text{d}{\it\tau}\;\{|\boldsymbol{Q}|^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }{\bf\xi}^{\ast }\times \boldsymbol{Q}+(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}^{\ast }){\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p+{\it\gamma}p(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}\},\end{eqnarray}$$
can be reduced to a form that can easily be minimised over
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\zeta}$
. After this,
${\it\zeta}$
. After this,
![]() ${\it\delta}W_{1}$
depends only on the radial displacement
${\it\delta}W_{1}$
depends only on the radial displacement
![]() ${\it\xi}$
and reduces to
${\it\xi}$
and reduces to
 $$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi})=\frac{{\rm\pi}}{2}\int _{a}^{b}\text{d}r\left[\,f\left(\frac{\text{d}{\it\xi}}{\text{d}r}\right)^{2}+g{\it\xi}^{2}\right],\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W_{1}({\bf\xi})=\frac{{\rm\pi}}{2}\int _{a}^{b}\text{d}r\left[\,f\left(\frac{\text{d}{\it\xi}}{\text{d}r}\right)^{2}+g{\it\xi}^{2}\right],\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle f=\frac{r(krB_{z}+mB_{{\it\theta}})^{2}}{k^{2}r^{2}+m^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f=\frac{r(krB_{z}+mB_{{\it\theta}})^{2}}{k^{2}r^{2}+m^{2}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle g=\frac{1}{r}\frac{(krB_{z}-mB_{{\it\theta}})^{2}}{k^{2}r^{2}+m^{2}}+\frac{1}{r}(krB_{z}+mB_{{\it\theta}})^{2}-\frac{2B_{{\it\theta}}}{r}\frac{\text{d}}{\text{d}r}(rB_{{\it\theta}})-\frac{\text{d}}{\text{d}r}\!\left(\frac{k^{2}r^{2}B_{z}^{2}-m^{2}B_{{\it\theta}}^{2}}{k^{2}r^{2}+m^{2}}\right). & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g=\frac{1}{r}\frac{(krB_{z}-mB_{{\it\theta}})^{2}}{k^{2}r^{2}+m^{2}}+\frac{1}{r}(krB_{z}+mB_{{\it\theta}})^{2}-\frac{2B_{{\it\theta}}}{r}\frac{\text{d}}{\text{d}r}(rB_{{\it\theta}})-\frac{\text{d}}{\text{d}r}\!\left(\frac{k^{2}r^{2}B_{z}^{2}-m^{2}B_{{\it\theta}}^{2}}{k^{2}r^{2}+m^{2}}\right). & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $-\infty <k<\infty$
and for
$-\infty <k<\infty$
and for
Equation (24.6) is a standard form,
and minimisation over
![]() ${\it\xi}$
leads to the Euler–Lagrange equation
${\it\xi}$
leads to the Euler–Lagrange equation
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}r}\!\left(\,f\,\frac{\text{d}{\it\xi}}{\text{d}r}\right)-g{\it\xi}=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}r}\!\left(\,f\,\frac{\text{d}{\it\xi}}{\text{d}r}\right)-g{\it\xi}=0.\end{eqnarray}$$
An important feature of (24.9) is that there is a singular point at the ‘resonant surface’ where
 $krB_{z}+mB_{{\it\theta}}=0$
and
$krB_{z}+mB_{{\it\theta}}=0$
and
![]() $f$
vanishes.
$f$
vanishes.
Suppose, first, that there is no resonant surface within the boundary at
![]() $r=b$
(which we take to be perfectly conducting), and that we integrate
(i.e. ‘project’) a solution of (24.9) from
$r=b$
(which we take to be perfectly conducting), and that we integrate
(i.e. ‘project’) a solution of (24.9) from
![]() $r=0$
,
$r=0$
,
![]() ${\it\xi}=0$
towards the boundary at
${\it\xi}=0$
towards the boundary at
![]() $r=b$
. (Of course, equation (24.9) has two independent solutions, but only one vanishes at the origin.)
Now, if this projected solution does not vanish anywhere before reaching the boundary
(see figure 55), then the plasma is stable for
that
$r=b$
. (Of course, equation (24.9) has two independent solutions, but only one vanishes at the origin.)
Now, if this projected solution does not vanish anywhere before reaching the boundary
(see figure 55), then the plasma is stable for
that
![]() $m$
and
$m$
and
![]() $k$
. Newcomb proves this mathematically, but we can see that it must be
true by the following simple argument.
$k$
. Newcomb proves this mathematically, but we can see that it must be
true by the following simple argument.

Figure 55. Projected displacement. A is the actual wall position and B is the hypothetical position needed for marginal stability.
The Euler–Lagrange equation (24.9)
is also the equation for marginal stability (
![]() ${\it\omega}^{2}=0$
) and it is clear that, if our projected solution does not vanish
before reaching the wall, then for the plasma to be marginally stable we would have
to move the wall (which has a stabilising effect) to a larger radius. Hence, with the
wall at its actual radius, the plasma must be stable.
${\it\omega}^{2}=0$
) and it is clear that, if our projected solution does not vanish
before reaching the wall, then for the plasma to be marginally stable we would have
to move the wall (which has a stabilising effect) to a larger radius. Hence, with the
wall at its actual radius, the plasma must be stable.
If there is a single resonant surface in the plasma, the argument is only a little
more complicated. In this case we ‘project’ two solutions of the marginal equation,
one outwards from
![]() $r=0$
,
$r=0$
,
![]() ${\it\xi}=0$
as before and the other inwards from the wall
${\it\xi}=0$
as before and the other inwards from the wall
![]() $r=b$
,
$r=b$
,
![]() ${\it\xi}=0$
. Then if neither of them vanishes before they reach the singular
surface, we have exactly the situation (see figure 15) that we discussed in § 5.1.
From that analysis we know that an ideal plasma is stable. Furthermore, we now know
that a resistive plasma is also stable if
${\it\xi}=0$
. Then if neither of them vanishes before they reach the singular
surface, we have exactly the situation (see figure 15) that we discussed in § 5.1.
From that analysis we know that an ideal plasma is stable. Furthermore, we now know
that a resistive plasma is also stable if
![]() ${\it\Delta}^{\prime }<0$
, where
${\it\Delta}^{\prime }<0$
, where
![]() ${\it\Delta}^{\prime }$
is the change in logarithmic derivative of
${\it\Delta}^{\prime }$
is the change in logarithmic derivative of
![]() ${\it\xi}$
, or the change in the small solution of (24.9) across the resonant surface (see
(5.6)).
${\it\xi}$
, or the change in the small solution of (24.9) across the resonant surface (see
(5.6)).
Before we turn to toroidal plasmas, note that the analysis of circular plasmas requires only the solution of the single differential equation (24.9).
25. Modes in toroidal systems
In a toroidal plasma, perturbations cannot be broken down into independent
one-dimensional Fourier modes, though in an axisymmetric torus they can be reduced to a
sum over independent two-dimensional modes
 ${\bf\xi}(r,{\it\theta})\exp (\text{i}n{\it\zeta})$
, where
${\bf\xi}(r,{\it\theta})\exp (\text{i}n{\it\zeta})$
, where
![]() ${\it\zeta}$
is the toroidal angle and
${\it\zeta}$
is the toroidal angle and
![]() ${\it\theta}$
is the poloidal angle. But, in fact, ballooning modes have a
completely different structure from the modes in a cylinder. They involve many, strongly
coupled, Fourier modes and therefore cannot be dealt with by retaining a limited number
of such modes.
${\it\theta}$
is the poloidal angle. But, in fact, ballooning modes have a
completely different structure from the modes in a cylinder. They involve many, strongly
coupled, Fourier modes and therefore cannot be dealt with by retaining a limited number
of such modes.
The principal characteristic of ballooning modes is that they have short wavelength
perpendicular to the magnetic field but long wavelength parallel to it. Specifically,
![]() $k_{\bot }a\ll 1$
and
$k_{\bot }a\ll 1$
and
![]() $k_{\Vert }R\sim 1$
, where
$k_{\Vert }R\sim 1$
, where
![]() $a$
and
$a$
and
![]() $R$
are the minor and major radii of the torus. (Note that, although
$R$
are the minor and major radii of the torus. (Note that, although
![]() $k_{\Vert }$
is small, it is not zero, as in a flute mode; see § 17.) Because of the long wavelength parallel to
$k_{\Vert }$
is small, it is not zero, as in a flute mode; see § 17.) Because of the long wavelength parallel to
![]() $\boldsymbol{B}$
, the stabilising effect of the magnetic field on ballooning modes is
weak and they are therefore among the most pervasive instabilities in a toroidal plasma.
Also, because of the short transverse wavelength, they are difficult to compute
directly.
$\boldsymbol{B}$
, the stabilising effect of the magnetic field on ballooning modes is
weak and they are therefore among the most pervasive instabilities in a toroidal plasma.
Also, because of the short transverse wavelength, they are difficult to compute
directly.
Ballooning modes occur in most plasma models – ideal MHD, resistive MHD, gyrofluid, gyrokinetic, etc. However, the theory is most easily explained in MHD, and we shall concentrate on this application.
In a torus, as we move along a field line, it passes through regions of stable curvature (
 ${\bf\kappa}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p<0$
, on the inner equator) and regions of unstable curvature (
${\bf\kappa}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p<0$
, on the inner equator) and regions of unstable curvature (
 ${\bf\kappa}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p>0$
, on the outer equator). A perturbation aligned with the field
therefore tends to be largest on the outer equator, where it bulges out (as does a weak
spot in a balloon!). However, this ballooning is opposed by the field line bending that
accompanies it, and the mode is a balance between these two effects. The amount of field
line bending associated with a given perturbation depends on the magnetic shear – which
therefore plays an important role in ballooning modes.
${\bf\kappa}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p>0$
, on the outer equator). A perturbation aligned with the field
therefore tends to be largest on the outer equator, where it bulges out (as does a weak
spot in a balloon!). However, this ballooning is opposed by the field line bending that
accompanies it, and the mode is a balance between these two effects. The amount of field
line bending associated with a given perturbation depends on the magnetic shear – which
therefore plays an important role in ballooning modes.
Historically, the significance of the ballooning effect was first noted in connection
with drift waves by Taylor (Reference Taylor1977), though in a
form that bears little resemblance to the later theory. The material in the following
sections is based upon various original sources. The idea that the coupling of almost
degenerate Fourier modes on adjacent surfaces could produce a radially extended mode was
introduced by Roberts & Taylor (Reference Roberts and Taylor1965), who
referred to the extended modes as ‘twisted slices’ (see figure 56), but they envisaged a nonlinear coupling rather than toroidal
coupling. (This oversight probably delayed the theory of ballooning modes by 20 years!)
The full theory for high-
![]() $n$
ballooning modes was given by Connor et al. (Reference Connor, Hastie and Taylor1978, Reference Connor, Hastie and Taylor1979a
,Reference Connor, Hastie and Taylor
b
). Independent approaches were developed by Glasser (Reference Glasser, Coppi and Sadowski1979) and Lee & Dam (Reference Lee, Van Dam, Coppi and Sadowski1979).
$n$
ballooning modes was given by Connor et al. (Reference Connor, Hastie and Taylor1978, Reference Connor, Hastie and Taylor1979a
,Reference Connor, Hastie and Taylor
b
). Independent approaches were developed by Glasser (Reference Glasser, Coppi and Sadowski1979) and Lee & Dam (Reference Lee, Van Dam, Coppi and Sadowski1979).

Figure 56. Twisted slicing mode (from Roberts & Taylor Reference Roberts and Taylor1965).
26. High mode number perturbations in an axisymmetric torus
As we mentioned above, in an axisymmetric torus perturbations can be reduced to
independent modes
 ${\sim}{\bf\xi}(r,{\it\theta})\exp (\text{i}n{\it\zeta})$
with toroidal mode number
${\sim}{\bf\xi}(r,{\it\theta})\exp (\text{i}n{\it\zeta})$
with toroidal mode number
![]() $n$
. We will consider first the limit of large toroidal mode number
$n$
. We will consider first the limit of large toroidal mode number
![]() $n$
and show that in this limit the oscillations on each magnetic surface
are decoupled and independent.
$n$
and show that in this limit the oscillations on each magnetic surface
are decoupled and independent.
The lowest order in an expansion in
![]() $1/\sqrt{n}$
of the scalar pressure energy functional
$1/\sqrt{n}$
of the scalar pressure energy functional
![]() ${\it\delta}W$
then defines a local frequency
${\it\delta}W$
then defines a local frequency
![]() ${\it\omega}^{2}({\it\Psi})$
on each surface, and determines the structure of the mode along the
magnetic field
${\it\omega}^{2}({\it\Psi})$
on each surface, and determines the structure of the mode along the
magnetic field
![]() $\boldsymbol{B}$
. Higher orders in the expansion determine the cross-field structure
and relate the local frequency
$\boldsymbol{B}$
. Higher orders in the expansion determine the cross-field structure
and relate the local frequency
![]() ${\it\omega}^{2}({\it\Psi})$
to the global frequency
${\it\omega}^{2}({\it\Psi})$
to the global frequency
![]() ${\it\Omega}^{2}$
– which finally determines stability of the system.
${\it\Omega}^{2}$
– which finally determines stability of the system.
The important discovery is that the local frequency
![]() ${\it\omega}^{2}({\it\Psi})$
, which requires only the solution of a one-dimensional ordinary
differential equation, nevertheless contains all the information necessary for the
complete solution of the global problem. The difficulty is that, before we can calculate
anything, we must find a representation for the perturbation that
reconciles the short perpendicular and long parallel wavelength with toroidal
periodicity in a sheared magnetic field.
${\it\omega}^{2}({\it\Psi})$
, which requires only the solution of a one-dimensional ordinary
differential equation, nevertheless contains all the information necessary for the
complete solution of the global problem. The difficulty is that, before we can calculate
anything, we must find a representation for the perturbation that
reconciles the short perpendicular and long parallel wavelength with toroidal
periodicity in a sheared magnetic field.
To represent short-wavelength disturbances,
![]() ${\it\phi}$
, in a medium that changes on a much longer scale, one normally uses an
‘eikonal’ or Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) form,
${\it\phi}$
, in a medium that changes on a much longer scale, one normally uses an
‘eikonal’ or Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) form,
 $$\begin{eqnarray}{\it\phi}\sim F\exp (\text{i}nS),\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}\sim F\exp (\text{i}nS),\end{eqnarray}$$
where
![]() $F$
and
$F$
and
![]() $S$
vary slowly, but the exponential varies rapidly when
$S$
vary slowly, but the exponential varies rapidly when
![]() $n$
is large. In the present case, the requirement for long parallel
wavelength means that we must have
$n$
is large. In the present case, the requirement for long parallel
wavelength means that we must have
 $$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0,\end{eqnarray}$$
but this is incompatible with periodicity around the
torus in a sheared field. For, if
![]() $S$
is constant along a line of force, then, following a line once around
the torus, one must have
$S$
is constant along a line of force, then, following a line once around
the torus, one must have
 $$\begin{eqnarray}S({\it\Psi},{\it\theta})-S\left({\it\Psi},~{\it\theta}+\frac{2{\rm\pi}}{q({\it\Psi})}\right)=\text{integer}\times \frac{2{\rm\pi}}{n}.\end{eqnarray}$$
$$\begin{eqnarray}S({\it\Psi},{\it\theta})-S\left({\it\Psi},~{\it\theta}+\frac{2{\rm\pi}}{q({\it\Psi})}\right)=\text{integer}\times \frac{2{\rm\pi}}{n}.\end{eqnarray}$$
Owing to the shear,
![]() $q({\it\Psi})$
varies from one magnetic surface to another, so this condition cannot
be satisfied everywhere without
$q({\it\Psi})$
varies from one magnetic surface to another, so this condition cannot
be satisfied everywhere without
![]() $S$
being discontinuous.
$S$
being discontinuous.
In the next section we show that a new representation allows us to combine the advantages of the eikonal with long parallel wavelength and toroidal periodicity.
26.1. Ballooning representation
After we have selected a single toroidal mode
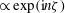 $\propto \exp (\text{i}n{\it\zeta})$
, the calculation of linear perturbations in an axisymmetric plasma
reduces to an eigenvalue equation of the form
$\propto \exp (\text{i}n{\it\zeta})$
, the calculation of linear perturbations in an axisymmetric plasma
reduces to an eigenvalue equation of the form
 $$\begin{eqnarray}{\mathcal{L}}({\it\theta},x)\,{\it\phi}({\it\theta},x)={\it\lambda}\,{\it\phi}({\it\theta},x),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}({\it\theta},x)\,{\it\phi}({\it\theta},x)={\it\lambda}\,{\it\phi}({\it\theta},x),\end{eqnarray}$$
where
![]() $x$
is a radial flux coordinate. The operator
$x$
is a radial flux coordinate. The operator
![]() ${\mathcal{L}}$
and the function
${\mathcal{L}}$
and the function
![]() ${\it\phi}$
are both periodic in poloidal angle
${\it\phi}$
are both periodic in poloidal angle
![]() ${\it\theta}$
.
${\it\theta}$
.
Now write
 $$\begin{eqnarray}{\it\phi}({\it\theta},x)=\mathop{\sum }_{m}\text{e}^{-\text{i}m{\it\theta}}\int _{-\infty }^{\infty }\text{e}^{\text{i}m{\it\eta}}\hat{{\it\phi}}({\it\eta},x)\,\text{d}{\it\eta}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\theta},x)=\mathop{\sum }_{m}\text{e}^{-\text{i}m{\it\theta}}\int _{-\infty }^{\infty }\text{e}^{\text{i}m{\it\eta}}\hat{{\it\phi}}({\it\eta},x)\,\text{d}{\it\eta}.\end{eqnarray}$$
This ensures that
![]() ${\it\phi}$
is periodic in
${\it\phi}$
is periodic in
![]() ${\it\theta}$
:
${\it\theta}$
:
![]() $\hat{{\it\phi}}$
does not need to be periodic. This ‘ballooning transform’ really
combines three steps:
$\hat{{\it\phi}}$
does not need to be periodic. This ‘ballooning transform’ really
combines three steps:
-
(i)
 ${\it\phi}\rightarrow$
a Fourier sum
${\it\phi}\rightarrow$
a Fourier sum
 $\sum _{m}a_{m}(x)\exp (-\text{i}m{\it\theta})$
;
$\sum _{m}a_{m}(x)\exp (-\text{i}m{\it\theta})$
; -
(ii)
 $a_{m}(x)$
is extended to a function
$a_{m}(x)$
is extended to a function
 $a(s,x)$
that coincides with
$a(s,x)$
that coincides with
 $a_{m}(x)$
when
$a_{m}(x)$
when
 $s=m$
;
$s=m$
; -
(iii)
 $a(s,x)$
is represented by a Fourier integral in
the coordinate
$a(s,x)$
is represented by a Fourier integral in
the coordinate
 ${\it\eta}$
.
${\it\eta}$
.
By direct substitution, it can be shown that
![]() $\hat{{\it\phi}}$
satisfies the same equation as
$\hat{{\it\phi}}$
satisfies the same equation as
![]() ${\it\phi}$
,
${\it\phi}$
,
 $$\begin{eqnarray}{\mathcal{L}}({\it\eta},x)\,\hat{{\it\phi}}({\it\eta},x)={\it\lambda}\,\hat{{\it\phi}}({\it\eta},x),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}({\it\eta},x)\,\hat{{\it\phi}}({\it\eta},x)={\it\lambda}\,\hat{{\it\phi}}({\it\eta},x),\end{eqnarray}$$
and has the same eigenvalues.
We have effectively taken a Fourier transform in step (i) and then reversed it in
step (ii). This is precisely why (26.6) is formally identified with (26.4). However the first transform was a Fourier
sum and the second was a Fourier integral;
consequently
![]() $\hat{{\it\phi}}$
does not have to be periodic.
$\hat{{\it\phi}}$
does not have to be periodic.
The extent to which (26.5) is
mathematically a true reversible transform, in the spirit of Fourier, Abel, etc., is
discussed at length in Connor et al. (Reference Connor, Hastie and Taylor1979b
), Hazeltine et al. (Reference Hazeltine, Hitchcock and Mahajan1981), Dewar & Glasser (Reference Dewar and Glasser1983)
and Hazeltine & Newcomb (Reference Hazeltine and Newcomb1990). This
highly mathematical discussion is not appropriate here; it is sufficient to note
that, as we will see below, when we introduce a WKBJ eikonal approximation for
![]() $\hat{{\it\phi}}$
in (26.5), we
obtain a stability criterion, and an estimate of the growth rates and the profiles of
unstable modes.
$\hat{{\it\phi}}$
in (26.5), we
obtain a stability criterion, and an estimate of the growth rates and the profiles of
unstable modes.
Another interpretation of (26.6) is that we have replaced the original stability problem, with its incompatible periodicity and wavelength requirements, by a fictitious problem in an infinite domain with no periodicity requirements, but which has the same eigenvalues. The operator is unchanged, so the short perpendicular and long parallel wavelength properties of the solution are unchanged.
The point of all of this is that, unlike
![]() ${\it\phi}$
,
${\it\phi}$
,
![]() $\hat{{\it\phi}}({\it\eta},x)$
can be represented in eikonal form,
$\hat{{\it\phi}}({\it\eta},x)$
can be represented in eikonal form,
 $$\begin{eqnarray}\hat{{\it\phi}}({\it\eta},x)=F({\it\eta},x)\exp (\text{i}nS),\end{eqnarray}$$
$$\begin{eqnarray}\hat{{\it\phi}}({\it\eta},x)=F({\it\eta},x)\exp (\text{i}nS),\end{eqnarray}$$
with
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0$
and both
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0$
and both
![]() $F$
and
$F$
and
![]() $S$
slowly varying.
$S$
slowly varying.
This perturbation has essentially the same form as the Roberts & Taylor (Reference Roberts and Taylor1965) ‘twisted slice’ quasi-mode, but this is no longer the actual perturbation. We will see later that the actual perturbation is a superposition of such ‘slices’.
Of course, as we no longer have the periodic boundary condition, we need a
replacement boundary condition for
![]() $\hat{{\it\phi}}({\it\eta},x)$
. This follows from the requirement that the transformation back to
$\hat{{\it\phi}}({\it\eta},x)$
. This follows from the requirement that the transformation back to
![]() ${\it\phi}({\it\eta},x)$
must lead to a physically acceptable function. Consequently,
${\it\phi}({\it\eta},x)$
must lead to a physically acceptable function. Consequently,
![]() ${\it\phi}$
must tend to zero sufficiently fast as
${\it\phi}$
must tend to zero sufficiently fast as
![]() $|{\it\eta}|\rightarrow 0$
for the integrals in (26.5) to converge.
$|{\it\eta}|\rightarrow 0$
for the integrals in (26.5) to converge.
27. Magnetohydrodynamic stability in a torus
In an axisymmetric torus the equilibrium field can be written as
 $$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\Psi}\times \boldsymbol{{\rm\nabla}}{\it\zeta}+I({\it\Psi})\boldsymbol{{\rm\nabla}}{\it\zeta},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\boldsymbol{{\rm\nabla}}{\it\Psi}\times \boldsymbol{{\rm\nabla}}{\it\zeta}+I({\it\Psi})\boldsymbol{{\rm\nabla}}{\it\zeta},\end{eqnarray}$$
where
![]() ${\it\Psi}$
defines the magnetic surface and
${\it\Psi}$
defines the magnetic surface and
![]() ${\it\zeta}$
is the toroidal angle around the torus. The first term gives the
poloidal field and the second the toroidal component (compare with the Grad–Shafranov
equilibrium in (2.19)).
${\it\zeta}$
is the toroidal angle around the torus. The first term gives the
poloidal field and the second the toroidal component (compare with the Grad–Shafranov
equilibrium in (2.19)).
In this section we denote the poloidal angle by
![]() ${\it\chi}$
to conform with Connor et al. (Reference Connor, Hastie and Taylor1979b
). Then, in the coordinates
${\it\chi}$
to conform with Connor et al. (Reference Connor, Hastie and Taylor1979b
). Then, in the coordinates
 $({\it\Psi},{\it\chi},{\it\zeta})$
, we have the line element
$({\it\Psi},{\it\chi},{\it\zeta})$
, we have the line element
 $$\begin{eqnarray}\text{d}s^{2}=\frac{1}{(RB_{{\it\chi}})^{2}}(\text{d}{\it\Psi})^{2}+(JB_{{\it\chi}})^{2}(\text{d}{\it\chi})^{2}+R^{2}(\text{d}{\it\zeta})^{2},\end{eqnarray}$$
$$\begin{eqnarray}\text{d}s^{2}=\frac{1}{(RB_{{\it\chi}})^{2}}(\text{d}{\it\Psi})^{2}+(JB_{{\it\chi}})^{2}(\text{d}{\it\chi})^{2}+R^{2}(\text{d}{\it\zeta})^{2},\end{eqnarray}$$
and the volume element
 $\text{d}{\it\tau}=J\,\text{d}{\it\Psi}\,\text{d}{\it\chi}\,\text{d}{\it\zeta}$
, with the Jacobian
$\text{d}{\it\tau}=J\,\text{d}{\it\Psi}\,\text{d}{\it\chi}\,\text{d}{\it\zeta}$
, with the Jacobian
 $J=|\boldsymbol{{\rm\nabla}}{\it\Psi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\chi}\times \boldsymbol{{\rm\nabla}}{\it\zeta}|^{-1}$
. A field line is defined by
$J=|\boldsymbol{{\rm\nabla}}{\it\Psi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\chi}\times \boldsymbol{{\rm\nabla}}{\it\zeta}|^{-1}$
. A field line is defined by
 ${\it\Psi}=\text{constant}$
,
${\it\Psi}=\text{constant}$
,
 ${\it\chi}={\it\chi}({\it\zeta})$
, where
${\it\chi}={\it\chi}({\it\zeta})$
, where
 $$\begin{eqnarray}\frac{\text{d}{\it\zeta}}{\text{d}{\it\chi}}=\frac{IJ}{R^{2}}\equiv {\it\nu}({\it\Psi}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}{\it\zeta}}{\text{d}{\it\chi}}=\frac{IJ}{R^{2}}\equiv {\it\nu}({\it\Psi}),\end{eqnarray}$$
and the safety factor is
 $$\begin{eqnarray}q({\it\Psi})=\frac{1}{2{\rm\pi}}\oint {\it\nu}\,\text{d}{\it\chi}.\end{eqnarray}$$
$$\begin{eqnarray}q({\it\Psi})=\frac{1}{2{\rm\pi}}\oint {\it\nu}\,\text{d}{\it\chi}.\end{eqnarray}$$
Turning now to the question of stability, we again take the scalar pressure energy principle,
 $$\begin{eqnarray}{\it\delta}W_{1}=\frac{1}{2}\int Q^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})+{\it\gamma}p(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}\,\text{d}{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}W_{1}=\frac{1}{2}\int Q^{2}-\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{Q}\times {\bf\xi}+({\bf\xi}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})+{\it\gamma}p(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi})^{2}\,\text{d}{\it\tau},\end{eqnarray}$$
and describe a perturbation
![]() ${\bf\xi}$
by the three components:
${\bf\xi}$
by the three components:
 $$\begin{eqnarray}\displaystyle X & = & \displaystyle RB_{{\it\chi}}{\it\xi}_{{\it\Psi}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X & = & \displaystyle RB_{{\it\chi}}{\it\xi}_{{\it\Psi}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle U & = & \displaystyle \displaystyle \left(\frac{{\it\xi}_{{\it\zeta}}}{R}-\frac{I}{R^{2}B_{{\it\chi}}}{\it\xi}_{{\it\chi}}\!\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U & = & \displaystyle \displaystyle \left(\frac{{\it\xi}_{{\it\zeta}}}{R}-\frac{I}{R^{2}B_{{\it\chi}}}{\it\xi}_{{\it\chi}}\!\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle Z & = & \displaystyle \displaystyle \frac{{\it\xi}_{{\it\chi}}}{B_{{\it\chi}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z & = & \displaystyle \displaystyle \frac{{\it\xi}_{{\it\chi}}}{B_{{\it\chi}}}.\end{eqnarray}$$
In terms of these components, the perturbed energy becomes
 $$\begin{eqnarray}\displaystyle {\it\delta}W & = & \displaystyle \frac{1}{2}\int J\,\text{d}{\it\Psi}\,\text{d}{\it\zeta}\,\text{d}{\it\chi}\,\Bigg\{\frac{B^{2}}{R^{2}B_{{\it\chi}}^{2}}|k_{\Vert }X|^{2}+\frac{R^{2}}{J^{2}}\,\Bigg|\frac{\partial U}{\partial {\it\chi}}-I\frac{\partial }{\partial {\it\Psi}}\Bigg(\frac{JX}{R^{2}}\Bigg)\Bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,B_{{\it\chi}}^{2}\,\Bigg|\text{i}nU+\frac{\partial X}{\partial {\it\Psi}}+\frac{j_{{\it\zeta}}}{RB_{{\it\chi}}^{2}}X\Bigg|^{2}-2K|X|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\gamma}p\,\Bigg|\frac{1}{J}\frac{\partial }{\partial {\it\Psi}}(JX)+\text{i}nU+\text{i}Bk_{\Vert }Z\Bigg|^{2}\Bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W & = & \displaystyle \frac{1}{2}\int J\,\text{d}{\it\Psi}\,\text{d}{\it\zeta}\,\text{d}{\it\chi}\,\Bigg\{\frac{B^{2}}{R^{2}B_{{\it\chi}}^{2}}|k_{\Vert }X|^{2}+\frac{R^{2}}{J^{2}}\,\Bigg|\frac{\partial U}{\partial {\it\chi}}-I\frac{\partial }{\partial {\it\Psi}}\Bigg(\frac{JX}{R^{2}}\Bigg)\Bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,B_{{\it\chi}}^{2}\,\Bigg|\text{i}nU+\frac{\partial X}{\partial {\it\Psi}}+\frac{j_{{\it\zeta}}}{RB_{{\it\chi}}^{2}}X\Bigg|^{2}-2K|X|^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\gamma}p\,\Bigg|\frac{1}{J}\frac{\partial }{\partial {\it\Psi}}(JX)+\text{i}nU+\text{i}Bk_{\Vert }Z\Bigg|^{2}\Bigg\},\end{eqnarray}$$
where
 $$\begin{eqnarray}\text{i}k_{\Vert }=\frac{1}{JB}\left(\frac{\partial }{\partial {\it\chi}}+\text{i}n{\it\nu}\right),\quad K=\frac{II^{\prime }}{R^{2}}\frac{\partial }{\partial {\it\Psi}}\ln R-\frac{\,j_{{\it\zeta}}}{R}\frac{\partial }{\partial {\it\Psi}}\ln (JB_{{\it\chi}}),\end{eqnarray}$$
$$\begin{eqnarray}\text{i}k_{\Vert }=\frac{1}{JB}\left(\frac{\partial }{\partial {\it\chi}}+\text{i}n{\it\nu}\right),\quad K=\frac{II^{\prime }}{R^{2}}\frac{\partial }{\partial {\it\Psi}}\ln R-\frac{\,j_{{\it\zeta}}}{R}\frac{\partial }{\partial {\it\Psi}}\ln (JB_{{\it\chi}}),\end{eqnarray}$$
and a prime denotes the derivative with respect to
![]() ${\it\Psi}$
. Minimisation of
${\it\Psi}$
. Minimisation of
![]() ${\it\delta}W$
over
${\it\delta}W$
over
![]() $Z$
makes the last term of (27.9) zero, corresponding to
$Z$
makes the last term of (27.9) zero, corresponding to
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}=0$
. Then minimisation over
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\xi}=0$
. Then minimisation over
![]() $U$
can be carried out as an expansion in
$U$
can be carried out as an expansion in
![]() $1/n$
. Correct to order
$1/n$
. Correct to order
![]() $1/n$
this requires
$1/n$
this requires
 $$\begin{eqnarray}\text{i}nU+\frac{\partial X}{\partial {\it\Psi}}+X\left(\frac{p^{\prime }}{B^{2}}+\frac{{\it\nu}^{\prime }}{{\it\nu}}\frac{I^{2}}{R^{2}B^{2}}\right)+\frac{I^{2}}{{\it\nu}R^{2}B^{2}}JBk_{\Vert }\left(\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\text{i}nU+\frac{\partial X}{\partial {\it\Psi}}+X\left(\frac{p^{\prime }}{B^{2}}+\frac{{\it\nu}^{\prime }}{{\it\nu}}\frac{I^{2}}{R^{2}B^{2}}\right)+\frac{I^{2}}{{\it\nu}R^{2}B^{2}}JBk_{\Vert }\left(\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right)=0,\end{eqnarray}$$
which reduces
![]() ${\it\delta}W$
to a form involving only the displacement
${\it\delta}W$
to a form involving only the displacement
![]() $X$
,
$X$
,
 $$\begin{eqnarray}\displaystyle {\it\delta}W & = & \displaystyle {\rm\pi}\int \text{d}{\it\Psi}\,\text{d}{\it\chi}\,\Bigg\{\frac{JB^{2}}{R^{2}B_{{\it\chi}}^{2}}|k_{\Vert }X|^{2}+\frac{R^{2}B_{{\it\chi}}^{2}}{JB^{2}}\,\Bigg|\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X)^{2}\Bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2J}{B^{2}}p^{\prime }\,\Bigg[|X|^{2}\frac{\partial }{\partial {\it\Psi}}\Bigg(p+\frac{B^{2}}{2}\Bigg)-\frac{\text{i}I}{JB^{2}}\frac{\partial }{\partial {\it\chi}}\Bigg(\frac{B^{2}}{2}\Bigg)\frac{X^{\ast }}{n}\frac{\partial X}{\partial {\it\Psi}}\Bigg]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{X^{\ast }}{n}\,JBk_{\Vert }(X{\it\sigma}^{\prime })-\frac{1}{n}[P^{\ast }JBk_{\Vert }Q+PJBk_{\Vert }^{\ast }Q^{\ast }]\Bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}W & = & \displaystyle {\rm\pi}\int \text{d}{\it\Psi}\,\text{d}{\it\chi}\,\Bigg\{\frac{JB^{2}}{R^{2}B_{{\it\chi}}^{2}}|k_{\Vert }X|^{2}+\frac{R^{2}B_{{\it\chi}}^{2}}{JB^{2}}\,\Bigg|\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X)^{2}\Bigg|^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2J}{B^{2}}p^{\prime }\,\Bigg[|X|^{2}\frac{\partial }{\partial {\it\Psi}}\Bigg(p+\frac{B^{2}}{2}\Bigg)-\frac{\text{i}I}{JB^{2}}\frac{\partial }{\partial {\it\chi}}\Bigg(\frac{B^{2}}{2}\Bigg)\frac{X^{\ast }}{n}\frac{\partial X}{\partial {\it\Psi}}\Bigg]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{X^{\ast }}{n}\,JBk_{\Vert }(X{\it\sigma}^{\prime })-\frac{1}{n}[P^{\ast }JBk_{\Vert }Q+PJBk_{\Vert }^{\ast }Q^{\ast }]\Bigg\},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle P & = & \displaystyle \displaystyle X{\it\sigma}-\frac{B_{{\it\chi}}^{2}}{{\it\nu}B^{2}}\frac{I}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P & = & \displaystyle \displaystyle X{\it\sigma}-\frac{B_{{\it\chi}}^{2}}{{\it\nu}B^{2}}\frac{I}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle Q & = & \displaystyle \displaystyle \frac{Xp^{\prime }}{B^{2}}+\frac{I^{2}}{{\it\nu}R^{2}B^{2}}\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q & = & \displaystyle \displaystyle \frac{Xp^{\prime }}{B^{2}}+\frac{I^{2}}{{\it\nu}R^{2}B^{2}}\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\sigma} & = & \displaystyle \displaystyle \frac{Ip^{\prime }}{B^{2}}+I^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\sigma} & = & \displaystyle \displaystyle \frac{Ip^{\prime }}{B^{2}}+I^{\prime }.\end{eqnarray}$$
To test for stability, we should now minimise (27.12) with respect to all functions
 $X({\it\Psi},{\it\chi})$
periodic in
$X({\it\Psi},{\it\chi})$
periodic in
![]() ${\it\chi}$
. However, in order to also derive a measure of the growth rate, or
frequency, of the ballooning modes, we need to introduce a suitable normalisation for
${\it\chi}$
. However, in order to also derive a measure of the growth rate, or
frequency, of the ballooning modes, we need to introduce a suitable normalisation for
![]() $X$
. We take
$X$
. We take
 $$\begin{eqnarray}{\rm\pi}\int J\,\text{d}{\it\Psi}\,\text{d}{\it\chi}\left\{\frac{|X|^{2}}{R^{2}B_{{\it\chi}}^{2}}+\left(\frac{RB_{{\it\chi}}}{B}\right)^{2}\left|\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right|^{2}\right\}=1,\end{eqnarray}$$
$$\begin{eqnarray}{\rm\pi}\int J\,\text{d}{\it\Psi}\,\text{d}{\it\chi}\left\{\frac{|X|^{2}}{R^{2}B_{{\it\chi}}^{2}}+\left(\frac{RB_{{\it\chi}}}{B}\right)^{2}\left|\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right|^{2}\right\}=1,\end{eqnarray}$$
which is the kinetic energy in the motion transverse to
![]() $\boldsymbol{B}$
. (This is more convenient than the total kinetic energy because it
does not involve
$\boldsymbol{B}$
. (This is more convenient than the total kinetic energy because it
does not involve
![]() $U$
or
$U$
or
![]() $Z$
.)
$Z$
.)
Then, minimising (27.12) subject to (27.16) gives the Euler–Lagrange equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle JBk_{\Vert }\left\{\frac{1}{JR^{2}B_{{\it\chi}}^{2}}\left[1-\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\right)^{2}\frac{1}{n^{2}}\frac{\partial ^{2}}{\partial {\it\Psi}^{2}}\right]JBk_{\Vert }X\right\}-\frac{2J}{B^{2}}Xp^{\prime }\frac{\partial }{\partial {\it\Psi}}\left(p+\frac{B^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\text{i}}{n}\frac{\partial X}{\partial {\it\Psi}}\frac{p^{\prime }I}{B^{4}}\frac{\partial B^{2}}{\partial {\it\chi}}-\frac{1}{n}JBk_{\Vert }\left[\frac{\partial }{\partial {\it\Psi}}\left(\frac{R^{2}B_{{\it\chi}}^{2}}{JB^{2}}\right)\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X)\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{n}JBk_{\Vert }({\it\sigma}^{\prime }X)-\frac{{\it\sigma}}{n}JBk_{\Vert }Q-\frac{p^{\prime }}{nB^{2}}JBk_{\Vert }P\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{n}JBk_{\Vert }\left\{\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left[\frac{IB_{{\it\chi}}^{2}}{{\it\nu}B^{2}}JBk_{\Vert }Q\right]\right\}+\frac{1}{n}JBk_{\Vert }\left\{\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left[\frac{I^{2}}{{\it\nu}R^{2}B^{2}}JBk_{\Vert }P\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\Omega}^{2}\left[\frac{J}{R^{2}B_{{\it\chi}}^{2}}X-\frac{JR^{2}B_{{\it\chi}}^{2}}{B^{2}}\frac{1}{n^{2}}\frac{\partial ^{2}X}{\partial {\it\Psi}^{2}}-\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left(\frac{JR^{2}B_{{\it\chi}}^{2}}{B^{2}}\right)\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle JBk_{\Vert }\left\{\frac{1}{JR^{2}B_{{\it\chi}}^{2}}\left[1-\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\right)^{2}\frac{1}{n^{2}}\frac{\partial ^{2}}{\partial {\it\Psi}^{2}}\right]JBk_{\Vert }X\right\}-\frac{2J}{B^{2}}Xp^{\prime }\frac{\partial }{\partial {\it\Psi}}\left(p+\frac{B^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\text{i}}{n}\frac{\partial X}{\partial {\it\Psi}}\frac{p^{\prime }I}{B^{4}}\frac{\partial B^{2}}{\partial {\it\chi}}-\frac{1}{n}JBk_{\Vert }\left[\frac{\partial }{\partial {\it\Psi}}\left(\frac{R^{2}B_{{\it\chi}}^{2}}{JB^{2}}\right)\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}(JBk_{\Vert }X)\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{n}JBk_{\Vert }({\it\sigma}^{\prime }X)-\frac{{\it\sigma}}{n}JBk_{\Vert }Q-\frac{p^{\prime }}{nB^{2}}JBk_{\Vert }P\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{n}JBk_{\Vert }\left\{\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left[\frac{IB_{{\it\chi}}^{2}}{{\it\nu}B^{2}}JBk_{\Vert }Q\right]\right\}+\frac{1}{n}JBk_{\Vert }\left\{\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left[\frac{I^{2}}{{\it\nu}R^{2}B^{2}}JBk_{\Vert }P\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\Omega}^{2}\left[\frac{J}{R^{2}B_{{\it\chi}}^{2}}X-\frac{JR^{2}B_{{\it\chi}}^{2}}{B^{2}}\frac{1}{n^{2}}\frac{\partial ^{2}X}{\partial {\it\Psi}^{2}}-\frac{1}{n}\frac{\partial }{\partial {\it\Psi}}\left(\frac{JR^{2}B_{{\it\chi}}^{2}}{B^{2}}\right)\frac{1}{n}\frac{\partial X}{\partial {\it\Psi}}\right].\end{eqnarray}$$
Recalling that
 $$\begin{eqnarray}\text{i}k_{\Vert }=\frac{1}{JB}\left(\frac{\partial }{\partial {\it\chi}}+\text{i}n{\it\nu}\right),\end{eqnarray}$$
$$\begin{eqnarray}\text{i}k_{\Vert }=\frac{1}{JB}\left(\frac{\partial }{\partial {\it\chi}}+\text{i}n{\it\nu}\right),\end{eqnarray}$$
we see that (27.17) is
a second-order partial differential equation in
![]() $\partial /\partial {\it\Psi}$
and
$\partial /\partial {\it\Psi}$
and
![]() $\partial /\partial {\it\chi}$
for the periodic function
$\partial /\partial {\it\chi}$
for the periodic function
 $X({\it\Psi},{\it\chi})$
, where
$X({\it\Psi},{\it\chi})$
, where
 $X({\it\Psi},{\it\chi}+{\it\chi}_{0})=X({\it\Psi},{\it\chi})$
and
$X({\it\Psi},{\it\chi}+{\it\chi}_{0})=X({\it\Psi},{\it\chi})$
and
 ${\it\chi}_{0}=\oint \text{d}{\it\chi}$
.
${\it\chi}_{0}=\oint \text{d}{\it\chi}$
.
We now introduce the ballooning transformation,
 $$\begin{eqnarray}X({\it\Psi},{\it\chi})=\mathop{\sum }_{m}\exp \left(-\frac{2{\rm\pi}\text{i}m{\it\chi}}{{\it\chi}_{0}}\right)\int _{-\infty }^{\infty }\text{d}y\,\exp \left(\frac{2{\rm\pi}\text{i}my}{{\it\chi}_{0}}\right)\hat{X}({\it\Psi},y).\end{eqnarray}$$
$$\begin{eqnarray}X({\it\Psi},{\it\chi})=\mathop{\sum }_{m}\exp \left(-\frac{2{\rm\pi}\text{i}m{\it\chi}}{{\it\chi}_{0}}\right)\int _{-\infty }^{\infty }\text{d}y\,\exp \left(\frac{2{\rm\pi}\text{i}my}{{\it\chi}_{0}}\right)\hat{X}({\it\Psi},y).\end{eqnarray}$$
This converts (27.17)
into an identical equation for
![]() $\hat{X}$
, with
$\hat{X}$
, with
![]() ${\it\chi}\rightarrow y$
, but now in the infinite domain
${\it\chi}\rightarrow y$
, but now in the infinite domain
 $-\infty <y<\infty$
and free of periodicity constraints. So we can write
$-\infty <y<\infty$
and free of periodicity constraints. So we can write
![]() $\hat{X}$
in eikonal form,
$\hat{X}$
in eikonal form,
 $$\begin{eqnarray}\hat{X}({\it\Psi},y)=F({\it\Psi},y)\exp \left(-\text{i}n\int _{y_{0}}^{y}{\it\nu}\,\text{d}y\right).\end{eqnarray}$$
$$\begin{eqnarray}\hat{X}({\it\Psi},y)=F({\it\Psi},y)\exp \left(-\text{i}n\int _{y_{0}}^{y}{\it\nu}\,\text{d}y\right).\end{eqnarray}$$
Note the appearance here of the arbitrary phase
![]() $y_{0}$
, which will be discussed below.
$y_{0}$
, which will be discussed below.
If we restore the toroidal mode number
 $\exp (\text{i}n{\it\zeta})$
, equation (27.20) is
equivalent to the eikonal (26.1),
$\exp (\text{i}n{\it\zeta})$
, equation (27.20) is
equivalent to the eikonal (26.1),
![]() $F\text{e}^{\text{i}nS}$
, with
$F\text{e}^{\text{i}nS}$
, with
 $S={\it\zeta}-\int \!{\it\nu}\,\text{d}{\it\chi}$
and
$S={\it\zeta}-\int \!{\it\nu}\,\text{d}{\it\chi}$
and
 $\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0$
. We have therefore reached the point where
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}S=0$
. We have therefore reached the point where
![]() $\hat{X}$
is in eikonal form, with
$\hat{X}$
is in eikonal form, with
![]() $F$
and
$F$
and
![]() $S$
varying slowly compared to the rapid variation across the field of the
phase
$S$
varying slowly compared to the rapid variation across the field of the
phase
 $\exp (\text{i}nS)$
.
$\exp (\text{i}nS)$
.
Now we invoke large
![]() $n$
, and introduce two length scales transverse to the magnetic surfaces:
(i) the equilibrium scale, which we continue to denote by
$n$
, and introduce two length scales transverse to the magnetic surfaces:
(i) the equilibrium scale, which we continue to denote by
![]() ${\it\Psi}$
, and (ii) a more rapid scale
${\it\Psi}$
, and (ii) a more rapid scale
 $x=\sqrt{n}({\it\Psi}-{\it\Psi}_{0})$
, where
$x=\sqrt{n}({\it\Psi}-{\it\Psi}_{0})$
, where
![]() ${\it\Psi}_{0}$
is to be identified later. This scale is related to the distance
between rational surfaces on which
${\it\Psi}_{0}$
is to be identified later. This scale is related to the distance
between rational surfaces on which
 $q({\it\Psi})=m/n$
. The separation between these surfaces tends to zero as
$q({\it\Psi})=m/n$
. The separation between these surfaces tends to zero as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Then, writing the transformed equation (27.17) as
 $$\begin{eqnarray}(L+{\it\Omega}^{2}M)F=0,\end{eqnarray}$$
$$\begin{eqnarray}(L+{\it\Omega}^{2}M)F=0,\end{eqnarray}$$
we expand in powers of
![]() $1/\sqrt{n}$
,
$1/\sqrt{n}$
,
 $$\begin{eqnarray}\displaystyle L & = & \displaystyle \displaystyle L_{0}+\frac{1}{\sqrt{n}}L_{1}+\frac{1}{n}L_{2}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L & = & \displaystyle \displaystyle L_{0}+\frac{1}{\sqrt{n}}L_{1}+\frac{1}{n}L_{2}+\cdots \,,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle M & = & \displaystyle \displaystyle M_{0}+\frac{1}{\sqrt{n}}M_{1}+\frac{1}{n}M_{2}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M & = & \displaystyle \displaystyle M_{0}+\frac{1}{\sqrt{n}}M_{1}+\frac{1}{n}M_{2}+\cdots \,.\end{eqnarray}$$
 $$\begin{eqnarray}[L_{0}+{\it\omega}^{2}({\it\Psi},y_{0})M_{0}]F_{0}=0,\end{eqnarray}$$
$$\begin{eqnarray}[L_{0}+{\it\omega}^{2}({\it\Psi},y_{0})M_{0}]F_{0}=0,\end{eqnarray}$$
where
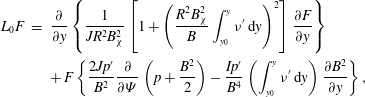 $$\begin{eqnarray}\displaystyle L_{0}F & = & \displaystyle \frac{\partial }{\partial y}\left\{\frac{1}{JR^{2}B_{{\it\chi}}^{2}}\left[1+\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)^{2}\right]\frac{\partial F}{\partial y}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,F\left\{\frac{2Jp^{\prime }}{B^{2}}\frac{\partial }{\partial {\it\Psi}}\left(p+\frac{B^{2}}{2}\right)-\frac{Ip^{\prime }}{B^{4}}\left(\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)\frac{\partial B^{2}}{\partial y}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{0}F & = & \displaystyle \frac{\partial }{\partial y}\left\{\frac{1}{JR^{2}B_{{\it\chi}}^{2}}\left[1+\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)^{2}\right]\frac{\partial F}{\partial y}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,F\left\{\frac{2Jp^{\prime }}{B^{2}}\frac{\partial }{\partial {\it\Psi}}\left(p+\frac{B^{2}}{2}\right)-\frac{Ip^{\prime }}{B^{4}}\left(\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)\frac{\partial B^{2}}{\partial y}\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle M_{0}F & = & \displaystyle \frac{J}{R^{2}B_{{\it\chi}}^{2}}\left[1+\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)^{2}\right]F.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{0}F & = & \displaystyle \frac{J}{R^{2}B_{{\it\chi}}^{2}}\left[1+\left(\frac{R^{2}B_{{\it\chi}}^{2}}{B}\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y\right)^{2}\right]F.\end{eqnarray}$$
The zeroth order equation (27.24) has the structure
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}y}\left(\!a+b\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\!\right)^{2}\frac{\text{d}F_{0}}{\text{d}y}+p^{\prime }\left(\!c+d\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\!\right)F_{0}=\displaystyle e\,{\it\omega}^{2}\left[a+b\left(\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\right)^{2}\right]F_{0}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}y}\left(\!a+b\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\!\right)^{2}\frac{\text{d}F_{0}}{\text{d}y}+p^{\prime }\left(\!c+d\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\!\right)F_{0}=\displaystyle e\,{\it\omega}^{2}\left[a+b\left(\int _{y_{0}}^{y}{\it\nu}^{\prime }\,\text{d}y^{\prime }\right)^{2}\right]F_{0}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
on each magnetic surface
![]() ${\it\Psi}$
. The coefficients
${\it\Psi}$
. The coefficients
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $d$
and
$d$
and
![]() $e$
are periodic in
$e$
are periodic in
![]() $y$
and defined on each surface by the equilibrium. The terms
$y$
and defined on each surface by the equilibrium. The terms
![]() $\int {\it\nu}^{\prime }\,\text{d}y$
increase indefinitely with
$\int {\it\nu}^{\prime }\,\text{d}y$
increase indefinitely with
![]() $y$
and show the strong effect of magnetic shear. The term
$y$
and show the strong effect of magnetic shear. The term
![]() $c$
represents the destabilising normal curvature, and
$c$
represents the destabilising normal curvature, and
![]() $d$
is related to the geodesic curvature.
$d$
is related to the geodesic curvature.
Equation (27.27) is a second-order
differential equation for
 ${\it\omega}^{2}({\it\Psi},y_{0})$
and can be readily solved numerically. To lowest order, therefore, the
oscillations on each surface are decoupled and each has a frequency
${\it\omega}^{2}({\it\Psi},y_{0})$
and can be readily solved numerically. To lowest order, therefore, the
oscillations on each surface are decoupled and each has a frequency
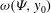 ${\it\omega}({\it\Psi},y_{0})$
that depends on the properties (curvature, shear, etc.) of that
surface and the, as yet unknown,
${\it\omega}({\it\Psi},y_{0})$
that depends on the properties (curvature, shear, etc.) of that
surface and the, as yet unknown,
![]() $y_{0}$
.
$y_{0}$
.
To calculate
 ${\it\omega}^{2}({\it\Psi},y_{0})$
, we need to apply the boundary conditions
${\it\omega}^{2}({\it\Psi},y_{0})$
, we need to apply the boundary conditions
![]() $F_{0}\rightarrow 0$
as
$F_{0}\rightarrow 0$
as
 $|y|\rightarrow \infty$
. Equation (27.24)
has two independent solutions at large
$|y|\rightarrow \infty$
. Equation (27.24)
has two independent solutions at large
![]() $|y|$
, but if
$|y|$
, but if
![]() ${\it\omega}^{2}<0$
one is exponentially growing and can be rejected. In this case, one
finds a discrete unstable eigenvalue spectrum. If
${\it\omega}^{2}<0$
one is exponentially growing and can be rejected. In this case, one
finds a discrete unstable eigenvalue spectrum. If
![]() ${\it\omega}^{2}>0$
both solutions behave like
${\it\omega}^{2}>0$
both solutions behave like
 $(1/y)\exp (\text{i}{\it\omega}y)$
at large
$(1/y)\exp (\text{i}{\it\omega}y)$
at large
![]() $|y|$
and both must be retained. Consequently, any positive
$|y|$
and both must be retained. Consequently, any positive
![]() ${\it\omega}^{2}$
is acceptable and in this case there is a continuous spectrum of
stable modes – as there is in a cylindrical plasma (Grad Reference Grad1973).
${\it\omega}^{2}$
is acceptable and in this case there is a continuous spectrum of
stable modes – as there is in a cylindrical plasma (Grad Reference Grad1973).
As (27.24) is a differential equation
in
![]() $y$
alone, any solution can be multiplied by an arbitrary function of
$y$
alone, any solution can be multiplied by an arbitrary function of
![]() $x$
, so the full solution in lowest order should be
$x$
, so the full solution in lowest order should be
 $$\begin{eqnarray}{\mathcal{F}}_{0}=A(x)F_{0}(y;{\it\Psi},y_{0}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{0}=A(x)F_{0}(y;{\it\Psi},y_{0}).\end{eqnarray}$$
It must be emphasised that, at this point, although the ‘local’ eigenvalue
 ${\it\omega}^{2}({\it\Psi},y_{0})$
and the eigenfunction
${\it\omega}^{2}({\it\Psi},y_{0})$
and the eigenfunction
 $F(y;{\it\Psi},y_{0})$
(which gives the perturbation along the field) can readily be
computed, we so far have no information on the profile
$F(y;{\it\Psi},y_{0})$
(which gives the perturbation along the field) can readily be
computed, we so far have no information on the profile
![]() $A(x)$
(perpendicular to the magnetic surfaces) or on the correct value for
$A(x)$
(perpendicular to the magnetic surfaces) or on the correct value for
![]() $y_{0}$
, or on the relation of
$y_{0}$
, or on the relation of
 ${\it\omega}^{2}({\it\Psi},y_{0})$
to the global eigenvalue
${\it\omega}^{2}({\it\Psi},y_{0})$
to the global eigenvalue
![]() ${\it\Omega}^{2}$
– which ultimately determines global stability. We will show later
that, when the theory is developed to higher order in
${\it\Omega}^{2}$
– which ultimately determines global stability. We will show later
that, when the theory is developed to higher order in
![]() $1/\sqrt{n}$
, these unknown factors are determined uniquely, and that all of the
information necessary to do so is already implicit in
$1/\sqrt{n}$
, these unknown factors are determined uniquely, and that all of the
information necessary to do so is already implicit in
 ${\it\omega}^{2}({\it\Psi},y_{0})$
.
${\it\omega}^{2}({\it\Psi},y_{0})$
.
27.1. Higher-order theory
As emphasised at the end of the previous section, to complete the theory of MHD stability in a torus, we still have to
-
(i) find the ‘envelope’
 $A(x)$
, which defines the structure of a ballooning mode across
the magnetic surfaces,
$A(x)$
, which defines the structure of a ballooning mode across
the magnetic surfaces, -
(ii) find
 ${\it\Psi}_{0}$
, which locates the surface on which the perturbation is
maximum,
${\it\Psi}_{0}$
, which locates the surface on which the perturbation is
maximum, -
(iii) find
 $y_{0}$
, which locates the poloidal angle at which the
perturbation is maximum,
$y_{0}$
, which locates the poloidal angle at which the
perturbation is maximum, -
(iv) relate the local
 ${\it\omega}^{2}({\it\Psi},y_{0})$
to the global eigenvalue
${\it\omega}^{2}({\it\Psi},y_{0})$
to the global eigenvalue
 ${\it\Omega}^{2}$
, which determines overall stability.
${\it\Omega}^{2}$
, which determines overall stability.
To find these quantities, we must proceed to higher order in the
![]() $1/\sqrt{n}$
expansion of (27.21). This involves the operators
$1/\sqrt{n}$
expansion of (27.21). This involves the operators
![]() $L_{1}$
,
$L_{1}$
,
![]() $L_{2}$
,
$L_{2}$
,
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
. The operators
$M_{2}$
. The operators
![]() $L_{1}$
and
$L_{1}$
and
![]() $M_{1}$
are
$M_{1}$
are
 $$\begin{eqnarray}L_{1}=-\text{i}\frac{1}{{\it\nu}^{\prime }(y_{0})}\frac{\partial L_{0}}{\partial y_{0}}\frac{\partial }{\partial x},\quad M_{1}=-\text{i}\frac{1}{{\it\nu}^{\prime }(y_{0})}\frac{\partial M_{0}}{\partial y_{0}}\frac{\partial }{\partial x},\end{eqnarray}$$
$$\begin{eqnarray}L_{1}=-\text{i}\frac{1}{{\it\nu}^{\prime }(y_{0})}\frac{\partial L_{0}}{\partial y_{0}}\frac{\partial }{\partial x},\quad M_{1}=-\text{i}\frac{1}{{\it\nu}^{\prime }(y_{0})}\frac{\partial M_{0}}{\partial y_{0}}\frac{\partial }{\partial x},\end{eqnarray}$$
and the next order equation is
 $$\begin{eqnarray}(L_{0}+{\it\omega}^{2}M_{0})F_{1}+(L_{1}+{\it\omega}^{2}M_{1})F_{0}=0.\end{eqnarray}$$
$$\begin{eqnarray}(L_{0}+{\it\omega}^{2}M_{0})F_{1}+(L_{1}+{\it\omega}^{2}M_{1})F_{0}=0.\end{eqnarray}$$
This can be solved for
![]() $F_{1}$
only if the integrability condition
$F_{1}$
only if the integrability condition
 $$\begin{eqnarray}\int _{-\infty }^{\infty }F_{0}(L_{1}+{\it\omega}^{2}M_{1})F_{0}\;\text{d}y=0\end{eqnarray}$$
$$\begin{eqnarray}\int _{-\infty }^{\infty }F_{0}(L_{1}+{\it\omega}^{2}M_{1})F_{0}\;\text{d}y=0\end{eqnarray}$$
is satisfied. From the form of
![]() $L_{1}$
and
$L_{1}$
and
![]() $M_{1}$
, it can be shown that this is equivalent to the constraint
$M_{1}$
, it can be shown that this is equivalent to the constraint
 $$\begin{eqnarray}\frac{\partial }{\partial y_{0}}{\it\omega}^{2}({\it\Psi},y_{0})=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial }{\partial y_{0}}{\it\omega}^{2}({\it\Psi},y_{0})=0.\end{eqnarray}$$
This fixes the undetermined parameter
![]() $y_{0}$
: on each magnetic surface it is at a minimum of
$y_{0}$
: on each magnetic surface it is at a minimum of
 ${\it\omega}^{2}({\it\Psi},y_{0})$
. Usually this is on the outer equator of the torus (Cooper Reference Cooper1988; Taylor Reference Taylor2012).
${\it\omega}^{2}({\it\Psi},y_{0})$
. Usually this is on the outer equator of the torus (Cooper Reference Cooper1988; Taylor Reference Taylor2012).
Proceeding further in the
![]() $1/\sqrt{n}$
expansion, in second order an integrability condition is obtained
involving the operators
$1/\sqrt{n}$
expansion, in second order an integrability condition is obtained
involving the operators
![]() $M_{2}$
and
$M_{2}$
and
![]() $L_{2}$
:
$L_{2}$
:
 $$\begin{eqnarray}\int [F_{0}(L_{1}+{\it\omega}^{2}M_{1})F_{1}+F_{0}(L_{2}+{\it\omega}^{2}M_{2})F_{0}+n({\it\Omega}^{2}-{\it\omega}^{2})F_{0}M_{0}F_{0}]\,\text{d}y=0.\end{eqnarray}$$
$$\begin{eqnarray}\int [F_{0}(L_{1}+{\it\omega}^{2}M_{1})F_{1}+F_{0}(L_{2}+{\it\omega}^{2}M_{2})F_{0}+n({\it\Omega}^{2}-{\it\omega}^{2})F_{0}M_{0}F_{0}]\,\text{d}y=0.\end{eqnarray}$$
If we choose
![]() ${\it\Psi}_{0}$
to be at a minimum, with respect to
${\it\Psi}_{0}$
to be at a minimum, with respect to
![]() ${\it\Psi}$
, of
${\it\Psi}$
, of
 ${\it\omega}^{2}({\it\Psi},y_{0})$
(with
${\it\omega}^{2}({\it\Psi},y_{0})$
(with
![]() $y_{0}$
fixed as above), then expanding
$y_{0}$
fixed as above), then expanding
![]() ${\it\omega}^{2}({\it\Psi})$
about this minimum, and using the properties of the operators
${\it\omega}^{2}({\it\Psi})$
about this minimum, and using the properties of the operators
![]() $L_{1}$
,
$L_{1}$
,
![]() $M_{1}$
,
$M_{1}$
,
![]() $L_{2}$
and
$L_{2}$
and
![]() $M_{2}$
, one eventually obtains from (27.33) an equation for
$M_{2}$
, one eventually obtains from (27.33) an equation for
![]() $A(x)$
:
$A(x)$
:
 $$\begin{eqnarray}\frac{\partial ^{2}{\it\omega}_{0}^{2}}{\partial y_{0}^{2}}\frac{\text{d}^{2}A}{\text{d}x^{2}}+({\it\nu}^{\prime }(y_{0}))^{2}\left[2n({\it\Omega}^{2}-{\it\omega}_{0}^{2})-\frac{\partial ^{2}{\it\omega}^{2}}{\partial {\it\Psi}^{2}}x^{2}\right]A(x)=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial ^{2}{\it\omega}_{0}^{2}}{\partial y_{0}^{2}}\frac{\text{d}^{2}A}{\text{d}x^{2}}+({\it\nu}^{\prime }(y_{0}))^{2}\left[2n({\it\Omega}^{2}-{\it\omega}_{0}^{2})-\frac{\partial ^{2}{\it\omega}^{2}}{\partial {\it\Psi}^{2}}x^{2}\right]A(x)=0.\end{eqnarray}$$
Therefore
 $$\begin{eqnarray}A(x)=\exp \left[-\frac{1}{2}|{\it\nu}^{\prime }(y_{0})|\left(\frac{\partial ^{2}{\it\omega}^{2}/\partial {\it\Psi}^{2}}{\partial ^{2}{\it\omega}^{2}/\partial y_{0}^{2}}\right)^{1/2}x^{2}\right]\end{eqnarray}$$
$$\begin{eqnarray}A(x)=\exp \left[-\frac{1}{2}|{\it\nu}^{\prime }(y_{0})|\left(\frac{\partial ^{2}{\it\omega}^{2}/\partial {\it\Psi}^{2}}{\partial ^{2}{\it\omega}^{2}/\partial y_{0}^{2}}\right)^{1/2}x^{2}\right]\end{eqnarray}$$
and
 $$\begin{eqnarray}{\it\Omega}^{2}={\it\omega}_{0}^{2}+\frac{1}{2n|{\it\nu}^{\prime }(y_{0})|}\left(\frac{\partial ^{2}{\it\omega}^{2}}{\partial {\it\Psi}^{2}}\frac{\partial ^{2}{\it\omega}^{2}}{\partial y_{0}^{2}}\right)^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\Omega}^{2}={\it\omega}_{0}^{2}+\frac{1}{2n|{\it\nu}^{\prime }(y_{0})|}\left(\frac{\partial ^{2}{\it\omega}^{2}}{\partial {\it\Psi}^{2}}\frac{\partial ^{2}{\it\omega}^{2}}{\partial y_{0}^{2}}\right)^{1/2}.\end{eqnarray}$$
This completes the theory, and shows that all the information needed to do so was
already contained in the lowest-order quantity
 ${\it\omega}^{2}({\it\Psi},y_{0})$
. In practice, therefore, we have only to compute solutions of the
differential equation (27.24). Note
also from (27.36) that ballooning
modes become more unstable as
${\it\omega}^{2}({\it\Psi},y_{0})$
. In practice, therefore, we have only to compute solutions of the
differential equation (27.24). Note
also from (27.36) that ballooning
modes become more unstable as
![]() $n\rightarrow \infty$
. This is precisely the region that is most difficult to calculate
by direct simulation and explains why ballooning theory filled an important gap in
the MHD theory of toroidal plasmas. (Of course, in reality MHD theory breaks down at
very high
$n\rightarrow \infty$
. This is precisely the region that is most difficult to calculate
by direct simulation and explains why ballooning theory filled an important gap in
the MHD theory of toroidal plasmas. (Of course, in reality MHD theory breaks down at
very high
![]() $n$
due to Larmor radius and other non-ideal effects.)
$n$
due to Larmor radius and other non-ideal effects.)
28. Applications
The first application of the theory was to a large-aspect-ratio torus, by Connor
et al. (Reference Connor, Hastie and Taylor1978). In this
so-called ‘
![]() $s{-}{\it\alpha}$
’ model, the coefficients of (27.27) can be expressed analytically and it becomes
$s{-}{\it\alpha}$
’ model, the coefficients of (27.27) can be expressed analytically and it becomes
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}y}[1+(s(y-y_{0})-{\it\alpha}\sin y)^{2}]\frac{\text{d}F}{\text{d}y}+{\it\alpha}[\cos y+\sin y\;(s(y-y_{0})-{\it\alpha}\sin y)]F=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}y}[1+(s(y-y_{0})-{\it\alpha}\sin y)^{2}]\frac{\text{d}F}{\text{d}y}+{\it\alpha}[\cos y+\sin y\;(s(y-y_{0})-{\it\alpha}\sin y)]F=0.\end{eqnarray}$$
Here
![]() $y_{0}$
is the parameter that locates the poloidal angle at which the mode
amplitude is maximum. It must be chosen to give the largest region of instability. The
parameter
$y_{0}$
is the parameter that locates the poloidal angle at which the mode
amplitude is maximum. It must be chosen to give the largest region of instability. The
parameter
![]() $s$
is a measure of the mean shear,
$s$
is a measure of the mean shear,
 $$\begin{eqnarray}s=\frac{\text{d}(\log q)}{\text{d}(\log r)},\end{eqnarray}$$
$$\begin{eqnarray}s=\frac{\text{d}(\log q)}{\text{d}(\log r)},\end{eqnarray}$$
and
![]() ${\it\alpha}$
is a measure of the pressure gradient,
${\it\alpha}$
is a measure of the pressure gradient,
 $$\begin{eqnarray}{\it\alpha}=-\frac{2Rq^{2}}{B^{2}}\frac{\text{d}p}{\text{d}r}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\alpha}=-\frac{2Rq^{2}}{B^{2}}\frac{\text{d}p}{\text{d}r}.\end{eqnarray}$$
Note that
![]() ${\it\omega}^{2}$
has been set to zero and (28.1) is therefore the marginal stability equation. It is then clear from
(28.3) that the ballooning
threshold, or maximum stable
${\it\omega}^{2}$
has been set to zero and (28.1) is therefore the marginal stability equation. It is then clear from
(28.3) that the ballooning
threshold, or maximum stable
![]() ${\it\beta}$
, will be of the form
${\it\beta}$
, will be of the form
 ${\it\beta}_{max}\sim (a/Rq^{2}){\it\alpha}(s)$
. We will see later (figure 58)
that over a range of
${\it\beta}_{max}\sim (a/Rq^{2}){\it\alpha}(s)$
. We will see later (figure 58)
that over a range of
![]() $s$
,
$s$
,
 ${\it\alpha}(s)\sim 1/3$
.
${\it\alpha}(s)\sim 1/3$
.
Numerical solutions of (28.1) for a
low-shear and a high-shear equilibrium are shown in figure 57. In the low-shear case
![]() $F$
shows strong remnants of the periodic behaviour, but, as expected,
these are suppressed in the high-shear case.
$F$
shows strong remnants of the periodic behaviour, but, as expected,
these are suppressed in the high-shear case.

Figure 57. Marginally stable eigenfunctions for (A) low shear,
![]() $s=0.1$
, and (B) high shear,
$s=0.1$
, and (B) high shear,
![]() $s=0.7$
(from Connor et al.
Reference Connor, Hastie and Taylor1978).
$s=0.7$
(from Connor et al.
Reference Connor, Hastie and Taylor1978).
The stability boundary computed for the
![]() $s{-}{\it\alpha}$
model is shown in figure 58. In
addition to the expected stability boundary ‘(a)’, there is a second boundary ‘(b)’.
Along the first boundary,
$s{-}{\it\alpha}$
model is shown in figure 58. In
addition to the expected stability boundary ‘(a)’, there is a second boundary ‘(b)’.
Along the first boundary,
![]() $y_{0}=0$
, corresponding to the usual mode ‘ballooning’ on the outer equator.
However, along the second boundary,
$y_{0}=0$
, corresponding to the usual mode ‘ballooning’ on the outer equator.
However, along the second boundary,
![]() $y_{0}$
is not zero, nor is it the symmetric value
$y_{0}$
is not zero, nor is it the symmetric value
![]() $y_{0}={\rm\pi}$
. In fact it is approximately
$y_{0}={\rm\pi}$
. In fact it is approximately
 $y_{0}=0.6{\rm\pi}$
, corresponding to a mode ‘ballooning’ at an intermediate angle between
the inner and outer equators. This is the result of the combined effect of normal and
geodesic curvature. (The line ‘(c)’ indicates where this boundary would be for
$y_{0}=0.6{\rm\pi}$
, corresponding to a mode ‘ballooning’ at an intermediate angle between
the inner and outer equators. This is the result of the combined effect of normal and
geodesic curvature. (The line ‘(c)’ indicates where this boundary would be for
![]() $y_{0}={\rm\pi}$
.)
$y_{0}={\rm\pi}$
.)

Figure 58. Stability boundaries for the
![]() $s{-}{\it\alpha}$
model obtained by taking (a)
$s{-}{\it\alpha}$
model obtained by taking (a)
![]() $y_{0}=0$
(solid line), (b)
$y_{0}=0$
(solid line), (b)
 $y_{0}=0.6{\rm\pi}$
(dot-dashed line) and (c)
$y_{0}=0.6{\rm\pi}$
(dot-dashed line) and (c)
![]() $y_{0}={\rm\pi}$
(dashed line).
$y_{0}={\rm\pi}$
(dashed line).

Figure 59. Variation of growth rate with toroidal mode number from direct MHD simulation
for an unstable JET configuration, with central safety factor
 $q_{0}=0.75$
, edge safety factor
$q_{0}=0.75$
, edge safety factor
![]() $q_{a}=6.4$
and average
$q_{a}=6.4$
and average
 ${\it\beta}=0.045$
. (Reproduced with permission from Sykes
et al. (Reference Sykes, Turner, Fielding and Haas1979).)
${\it\beta}=0.045$
. (Reproduced with permission from Sykes
et al. (Reference Sykes, Turner, Fielding and Haas1979).)
Calculations for more realistic configurations include those for the JET experiment
(Sykes et al.
Reference Sykes, Turner, Fielding and Haas1979). The result for an unstable JET plasma is
shown in figure 59. Here the calculations are for
the true, low-aspect-ratio, toroidal configuration, with the true D-shaped cross-section
and realistic pressure profile. The figure includes the growth rates computed from the
ballooning equation for the
![]() $n\rightarrow \infty$
limit, and the
$n\rightarrow \infty$
limit, and the
![]() $1/n$
corrections for large but finite
$1/n$
corrections for large but finite
![]() $n$
(the spread in the
$n$
(the spread in the
![]() $1/n$
contribution reflects the limitations of numerical representation, and
subsequent differentiations, of the equilibrium profiles). The figure also shows the
growth rate for low-
$1/n$
contribution reflects the limitations of numerical representation, and
subsequent differentiations, of the equilibrium profiles). The figure also shows the
growth rate for low-
![]() $n$
modes (
$n$
modes (
 $n=1,2,3,4$
) computed using two-dimensional MHD codes. (These low-
$n=1,2,3,4$
) computed using two-dimensional MHD codes. (These low-
![]() $n$
modes can be computed directly, as they do not require high
resolution.) An important feature of figure 59 is
that the growth rates
$n$
modes can be computed directly, as they do not require high
resolution.) An important feature of figure 59 is
that the growth rates
![]() ${\it\gamma}^{2}(n)$
calculated from the high-
${\it\gamma}^{2}(n)$
calculated from the high-
![]() $n$
ballooning theory join smoothly to the low-
$n$
ballooning theory join smoothly to the low-
![]() $n$
computations, with the cross-over occurring at approximately
$n$
computations, with the cross-over occurring at approximately
![]() $n=4$
or 5. Thus we can be confident that our overall picture of ideal MHD
toroidal modes is complete.
$n=4$
or 5. Thus we can be confident that our overall picture of ideal MHD
toroidal modes is complete.
The effect of changing cross-section on ballooning modes was investigated by Todd
et al. (Reference Todd, Manickam, Okabayashi, Chance, Grimm, Greene and Johnson1979) for plasma in a
torus with the idealised D-shaped cross-section shown in figure 60. The parameters
![]() ${\it\delta}$
and
${\it\delta}$
and
![]() ${\it\kappa}$
, respectively, define the triangularity and ellipticity of the
boundary,
${\it\kappa}$
, respectively, define the triangularity and ellipticity of the
boundary,
 $X=X_{0}+a\cos ({\it\theta}+{\it\delta}\sin {\it\theta})$
,
$X=X_{0}+a\cos ({\it\theta}+{\it\delta}\sin {\it\theta})$
,
 $Z={\it\kappa}a\sin {\it\theta}$
, and
$Z={\it\kappa}a\sin {\it\theta}$
, and
![]() ${\it\alpha}$
describes the peaking of the pressure profile,
${\it\alpha}$
describes the peaking of the pressure profile,
 $p({\it\Psi})\propto ({\it\Psi}_{b}-{\it\Psi})^{{\it\alpha}}$
. Figure 61 shows two examples of
the maximum
$p({\it\Psi})\propto ({\it\Psi}_{b}-{\it\Psi})^{{\it\alpha}}$
. Figure 61 shows two examples of
the maximum
![]() ${\it\beta}$
for modes of different
${\it\beta}$
for modes of different
![]() $n$
, both for plasma in a perfectly conducting shell, as in the previous
examples, and for a ‘free-boundary’ plasma with the wall effectively at infinity. Here
again the high-
$n$
, both for plasma in a perfectly conducting shell, as in the previous
examples, and for a ‘free-boundary’ plasma with the wall effectively at infinity. Here
again the high-
![]() $n$
calculations link smoothly to the low-
$n$
calculations link smoothly to the low-
![]() $n$
computations. Note that, in the free-boundary example in figure 61(b), the
$n$
computations. Note that, in the free-boundary example in figure 61(b), the
![]() $n=1$
mode imposes a more stringent limit on
$n=1$
mode imposes a more stringent limit on
![]() ${\it\beta}$
than does the
${\it\beta}$
than does the
![]() $n\rightarrow \infty$
. But
$n\rightarrow \infty$
. But
![]() $n\rightarrow \infty$
is still the most stringent of the higher-
$n\rightarrow \infty$
is still the most stringent of the higher-
![]() $n$
modes as the theory requires.
$n$
modes as the theory requires.

Figure 60. Geometry used to study ballooning stability. (Reproduced with permission from Todd et al. (Reference Todd, Manickam, Okabayashi, Chance, Grimm, Greene and Johnson1979).)

Figure 61. Critical
![]() ${\it\beta}$
as a function of
${\it\beta}$
as a function of
![]() $1/n$
for a configuration with (a)
$1/n$
for a configuration with (a)
 $R/a=3.5$
,
$R/a=3.5$
,
 ${\it\kappa}=1.65$
,
${\it\kappa}=1.65$
,
![]() ${\it\delta}=0.25$
,
${\it\delta}=0.25$
,
![]() ${\it\alpha}=1.4$
and
${\it\alpha}=1.4$
and
 $1.0<q<3.0$
and (b)
$1.0<q<3.0$
and (b)
 $R/a=4.6$
,
$R/a=4.6$
,
![]() ${\it\kappa}=1.0$
,
${\it\kappa}=1.0$
,
![]() ${\it\delta}=0$
,
${\it\delta}=0$
,
![]() ${\it\alpha}=2$
and
${\it\alpha}=2$
and
 $1.04<q<1.58$
. (Reproduced with permission from Todd
et al. (Reference Todd, Manickam, Okabayashi, Chance, Grimm, Greene and Johnson1979).)
$1.04<q<1.58$
. (Reproduced with permission from Todd
et al. (Reference Todd, Manickam, Okabayashi, Chance, Grimm, Greene and Johnson1979).)
29. Validity of ballooning theory
Now that we have seen the power and usefulness of the ballooning theory, it is
appropriate to ask the following: When should perturbations in a torus be interpreted as
ballooning modes and when should they be described by conventional Fourier modes – as in
a straight cylinder (Connor & Taylor Reference Connor and Taylor1987)?
The parameter that determines this, which in the mathematical analysis we took to be ‘
![]() $1/n$
’, is physically
$1/n$
’, is physically
 $$\begin{eqnarray}g=\left(\frac{\text{coupling between Fourier modes resonant on adjacent surfaces}}{\text{difference in frequency between Fourier modes resonant on adjacent surfaces}}\right),\end{eqnarray}$$
$$\begin{eqnarray}g=\left(\frac{\text{coupling between Fourier modes resonant on adjacent surfaces}}{\text{difference in frequency between Fourier modes resonant on adjacent surfaces}}\right),\end{eqnarray}$$
and ballooning theory is valid when
![]() $g$
is large.
$g$
is large.
The difference in frequency between Fourier modes is actually
![]() $\propto 1/ns$
, so that the theory is always valid as
$\propto 1/ns$
, so that the theory is always valid as
![]() $n\rightarrow \infty$
unless the shear
$n\rightarrow \infty$
unless the shear
![]() $s$
is small or vanishes (as it does in so-called ‘reverse-shear’
equilibria). A discussion of the ‘small-shear’ situation is given in Hastie & Taylor
(Reference Hastie and Taylor1981) and Connor & Hastie (Reference Connor and Hastie2004).
$s$
is small or vanishes (as it does in so-called ‘reverse-shear’
equilibria). A discussion of the ‘small-shear’ situation is given in Hastie & Taylor
(Reference Hastie and Taylor1981) and Connor & Hastie (Reference Connor and Hastie2004).
30. Mode structure
If we want to see the true structure of a ballooning mode, we must construct the
physical perturbation
![]() ${\it\phi}$
from the ‘fictitious’ perturbation
${\it\phi}$
from the ‘fictitious’ perturbation
![]() $\hat{{\it\phi}}$
. That is, we must reverse the ballooning transformation (27.19) and (27.20) by evaluating the right-hand side of
$\hat{{\it\phi}}$
. That is, we must reverse the ballooning transformation (27.19) and (27.20) by evaluating the right-hand side of
 $$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{m}\text{e}^{-\text{i}m{\it\theta}}\int _{-\infty }^{\infty }\text{e}^{\text{i}my}\text{e}^{-\text{i}nq({\it\Psi})y}F({\it\Psi},y)\,\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{m}\text{e}^{-\text{i}m{\it\theta}}\int _{-\infty }^{\infty }\text{e}^{\text{i}my}\text{e}^{-\text{i}nq({\it\Psi})y}F({\it\Psi},y)\,\text{d}y.\end{eqnarray}$$
Several interesting consequences follow from (30.1). If we carry out the integration
over
![]() $y$
, the result is clearly a function of
$y$
, the result is clearly a function of
 $(m-nq)$
and
$(m-nq)$
and
 $$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{m}U(m-nq)\text{e}^{-\text{i}m{\it\theta}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{m}U(m-nq)\text{e}^{-\text{i}m{\it\theta}}.\end{eqnarray}$$
This is a sum of similar contributions, each centred on a different
rational surface, precisely as we would expect since neighbouring rational surfaces are
almost degenerate after an appropriate realignment on each surface to compensate for the
change in direction of
![]() $\boldsymbol{B}$
; see § 25. This degeneracy
becomes exact as
$\boldsymbol{B}$
; see § 25. This degeneracy
becomes exact as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Equation (30.1) also provides another way of looking at the ballooning transform. If we write (30.1) as
 $$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\int _{-\infty }^{\infty }\mathop{\sum }_{m}\text{e}^{-\text{i}m({\it\theta}-y)}\text{e}^{\text{i}nq({\it\Psi})y}F({\it\Psi},y)\,\text{d}y,\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\int _{-\infty }^{\infty }\mathop{\sum }_{m}\text{e}^{-\text{i}m({\it\theta}-y)}\text{e}^{\text{i}nq({\it\Psi})y}F({\it\Psi},y)\,\text{d}y,\end{eqnarray}$$
and assume convergence, we can take the sum
 $\sum _{m}\text{e}^{-\text{i}m({\it\theta}-y)}$
to be the Fourier series for the periodic function
$\sum _{m}\text{e}^{-\text{i}m({\it\theta}-y)}$
to be the Fourier series for the periodic function
 $\sum _{N}{\it\delta}({\it\theta}-y-2{\rm\pi}N)$
. Then
$\sum _{N}{\it\delta}({\it\theta}-y-2{\rm\pi}N)$
. Then
 $$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{N}\text{e}^{-\text{i}nq({\it\theta}-2{\rm\pi}N)}F({\it\Psi},{\it\theta}-2{\rm\pi}N),\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\Psi},{\it\theta})=\mathop{\sum }_{N}\text{e}^{-\text{i}nq({\it\theta}-2{\rm\pi}N)}F({\it\Psi},{\it\theta}-2{\rm\pi}N),\end{eqnarray}$$
in which the periodic perturbation is constructed from the non-periodic
function
![]() $F$
by adding an infinite number of repetitions of it spaced at multiples
of
$F$
by adding an infinite number of repetitions of it spaced at multiples
of
![]() $2{\rm\pi}$
(see figure 62).
$2{\rm\pi}$
(see figure 62).

Figure 62. Constructing the ballooning perturbation from an infinite set of displaced functions.
Yet another view is obtained by restoring the toroidal mode number
 $\exp (\text{i}n{\it\zeta})$
, in each term of the sum (30.4). Each term then has the form
$\exp (\text{i}n{\it\zeta})$
, in each term of the sum (30.4). Each term then has the form
 $$\begin{eqnarray}F({\it\Psi},{\it\theta})\text{e}^{-\text{i}n(q({\it\Psi}){\it\theta}-{\it\zeta})},\end{eqnarray}$$
$$\begin{eqnarray}F({\it\Psi},{\it\theta})\text{e}^{-\text{i}n(q({\it\Psi}){\it\theta}-{\it\zeta})},\end{eqnarray}$$
which is essentially the ‘twisted slice’ mentioned at the start of this study (see § 25).
31. Conclusion
Before ballooning theory, only low-
![]() $n$
modes could be studied theoretically in a toroidal plasma, whereas in
a cylindrical plasma all modes could be analysed from a single second-order ordinary
differential equation. Ballooning theory makes it possible to study high-
$n$
modes could be studied theoretically in a toroidal plasma, whereas in
a cylindrical plasma all modes could be analysed from a single second-order ordinary
differential equation. Ballooning theory makes it possible to study high-
![]() $n$
modes in a torus – again from a single second-order ordinary
differential equation. In this sense the realistic toroidal problem has become as
amenable to theoretical analysis as the idealised cylindrical one!
$n$
modes in a torus – again from a single second-order ordinary
differential equation. In this sense the realistic toroidal problem has become as
amenable to theoretical analysis as the idealised cylindrical one!
Acknowledgements
The contributions of R. J. Hastie to these lecture notes are gratefully acknowledged, as are numerous helpful discussions with J. W. Connor and C. J. Ham. This work has been part-funded by the RCUK Energy Programme (grant number EP/I501045).