No CrossRef data available.
Article contents
Small-amplitude Langmuir pulse excited by a planar grid electrode in a flowing plasma
Published online by Cambridge University Press: 13 July 2015
Abstract
The generation and propagation of a small-amplitude Langmuir pulse excited by a planar grid electrode in a spatially uniform collisionless plasma with a constant flow velocity is studied by solving the linearized Vlasov–Poisson equations. The electrode is transparent to the flow of particles, like a screen or a wire mesh. The particles are assumed to have a Kappa velocity distribution, a reasonable approximation for electron distribution functions in the solar wind. Exact, closed-form solutions are obtained for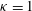 
${\it\kappa}=1$ , the Lorentzian distribution, and for 
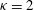${\it\kappa}=2$ . The explicit form of the solution in the case 
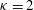${\it\kappa}=2$ has not, to our knowledge, appeared in the literature before. The properties of the solutions are investigated and a practical technique for measuring the bulk flow velocity in plasma experiments is proposed that may be useful for high-accuracy, high-time-resolution measurements of the bulk flow velocity in the solar wind.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2015
References
Abramowitz, M. & Stegun, I. A.(Eds) 1972
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing, US Department of Commerce, National Bureau of Standards.Google Scholar
Borovsky, J. E.
1988
The dynamic sheath – objects coupling to plasmas on electron–plasma-frequency time scales. Phys. Fluids
31, 1074–1100.CrossRefGoogle Scholar
Buckley, R.
1968
Radio frequency properties of a plane grid capacitor immersed in a hot collision-free plasma. J. Plasma Phys.
2, 339–351.CrossRefGoogle Scholar
Calder, A. C., Hulbert, G. W. & Laframboise, J. G.
1993
Sheath dynamics of electrodes stepped to large negative potentials. Phys. Fluids B
5, 674–690.CrossRefGoogle Scholar
Couturier, P., Hoang, S., Meyer-Vernet, N. & Steinberg, J. L.
1981
Quasi-thermal noise in a stable plasma at rest – theory and observations from ISEE 3. J. Geophys. Res.
86, 11127–11138.CrossRefGoogle Scholar
Crawford, F. W. & Harp, R. S.
1965
The resonance probe – a tool for ionospheric and space research. J. Geophys. Res.
70, 587–596.CrossRefGoogle Scholar
Drummond, W. E.
1963
Theory of plasma wave probes in a collisionless plasma. Rev. Sci. Instrum.
34, 779–781.CrossRefGoogle Scholar
Feix, M.
1964
Excitation level of plasma oscillations. Phys. Lett.
9, 123–125.CrossRefGoogle Scholar
Fried, B. D., Kaufman, A. N. & Sachs, D. L.
1966
Low-frequency spatial response of a collisional electron plasma. Phys. Fluids
9, 292–298.CrossRefGoogle Scholar
Maksimovic, M., Pierrard, V. & Riley, P.
1997
Ulysses electron distributions fitted with Kappa functions. Geophys. Res. Lett.
24, 1151–1154.CrossRefGoogle Scholar
Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., Marsch, E., McComas, D. J., Salem, C., Lin, R. P. & Elliott, H.
2005
Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU. J. Geophys. Res.
110, A09104, doi:10.1029/2005JA011119.Google Scholar
Meyer-Vernet, N.
1979
On natural noises detected by antennas in plasmas. J. Geophys. Res.
84, 5373–5377.CrossRefGoogle Scholar
Meyer-Vernet, N., Hoang, S., Issautier, K., Maksimovic, M., Manning, R., Moncuquet, M. & Stone, R. G.
1998
Measuring plasma parameters with thermal noise spectroscopy. In Measurement Techniques in Space Plasmas – Fields (ed. Pfaff, R. F., Borovsky, J. E. & Young, D. T.), Geophysical Monograph Series, vol. 103, pp. 205–210. American Geophysical Union.CrossRefGoogle Scholar
Meyer-Vernet, N. & Perche, C.
1989
Tool kit for antennae and thermal noise near the plasma frequency. J. Geophys. Res.
94, 2405–2415.CrossRefGoogle Scholar
Pierrard, V. & Lazar, M.
2010
Kappa distributions: theory and applications in space plasmas. Solar Phys.
267, 153–174.CrossRefGoogle Scholar
Podesta, J. J.
2005
Spatial Landau damping in plasmas with three-dimensional
${\it\kappa}$
distributions. Phys. Plasmas
12, 052101.CrossRefGoogle Scholar
${\it\kappa}$
distributions. Phys. Plasmas
12, 052101.CrossRefGoogle ScholarPodesta, J. J.
2008
Landau damping in relativistic plasmas with power-law distributions and applications to solar wind electrons. Phys. Plasmas
15 (12), 122902.CrossRefGoogle Scholar
Simonen, T. C.
1970
Grid assemblies as electrostatic plasma wave antennas. In Plasma Waves in Space and in the Laboratory (ed. Thomas, J. O. & Landmark, B. J.), vol. 2, pp. 285–296. American Elsevier.Google Scholar
Thorne, R. M. & Summers, D.
1991
Landau damping in space plasmas. Phys. Fluids B
3, 2117–2123.CrossRefGoogle Scholar
Vasyliunas, V. M.
1968
A survey of low-energy electrons in the evening sector of the magnetosphere with Ogo 1 and Ogo 3. J. Geophys. Res.
73, 2839–2884.CrossRefGoogle Scholar
Wang, L., Lin, R. P., Salem, C., Pulupa, M., Larson, D. E., Yoon, P. H. & Luhmann, J. G.
2012
Quiet-time interplanetary 2–20 keV superhalo electrons at solar minimum. Astrophys. J. Lett.
753, L23.CrossRefGoogle Scholar
Wang, L., Lin, R. P., Salem, C., Pulupa, M., Larson, D. E., Yoon, P. H. & Luhmann, J. G.
2013
Quiet-time solar wind superhalo electrons at solar minimum. In Solar Wind 13: Proceedings of the Thirteenth International Solar Wind Conference. American Institute of Physics Conference Proceedings (ed. Zank, G. P., Borovsky, J., Bruno, R., Cirtain, J., Cranmer, S., Elliott, H., Giacalone, J., Gonzalez, W., Li, G., Marsch, E., Moebius, E., Pogorelov, N., Spann, J. & Verkhoglyadova, O.), vol. 1539, pp. 299–302.Google Scholar