Article contents
A simple model for internal transport barrier induced by fishbone in tokamak plasmas
Published online by Cambridge University Press: 28 December 2023
Abstract
Fishbone bursts have been observed to strongly correlate to internal transport barrier (ITB) formation in a number of tokamak devices. A simple model incorporating the fishbone dynamics and ion pressure gradient evolution is proposed in order to investigate the key physics parameters assisting the triggering of ITB. The time evolution of fishbone is described by the well-known predator–prey model. For each burst cycle, the energetic particles (EPs) resonantly interact with fishbone and are radially expelled from inner region leading to a radial current. A compensating bulk plasma return current and, hence, poloidal flow can be induced if the fishbone cycle frequency is greater than the poloidal flow damping rate. When the shear of the poloidal flow exceeds a critical value, the turbulent fluctuations are suppressed and the bulk ion pressure gradient transits to the high-confinement state. It is shown that this process is only sensitive to the deposition rate of the trapped EPs within the $q=1$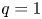 surface, but not sensitive to other parameters. A quantitative formula for the shearing rate of poloidal flow induced by fishbone bursts is derived and verified numerically.
surface, but not sensitive to other parameters. A quantitative formula for the shearing rate of poloidal flow induced by fishbone bursts is derived and verified numerically.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



