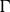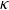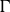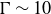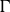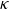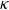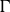1. Introduction
Solitons are stable, localized wave packets that maintain their shape and speed while propagating through a medium. They arise due to a delicate balance between nonlinear and dispersive effects, making them a fascinating subject of study in various fields of physics (Gu, Reference Gu2013, Arora, Rani & Emadifar, Reference Arora, Rani and Emadifar2022). Solitons can be found in numerous settings, including water waves (Craig et al. Reference Craig, Guyenne, Hammack, Henderson and Sulem2006), optical fibres (Gordon, Reference Gordon1983), carbon nanotubes systems (Chamon, Reference Chamon2000, Kumar et al. Reference Kumar, Vij, Kant and Thakur2022), charged fluids and even biological systems (Gu, Reference Gu2013, Arora, Rani & Emadifar, Reference Arora, Rani and Emadifar2022). Dusty plasma offers a unique opportunity to study the characteristics of solitons in charged fluids on very accessible spatiotemproal scale (Shukla, Reference Shukla1983). The interaction of the dust particles can be modelled by Yukawa potential, characterizing with the coupling parameter
$\Gamma = Q^{2}/aT$
and the screening parameter
$\kappa = a/\lambda _{d}$
, where
$Q$
,
$T$
,
$a$
and
$\lambda _{d}$
are the dust charge, dust temperature, lattice constant and screening length, respectively.
These nonlinear excitations in the strongly coupled regime of the medium are well explored using various theoretical models, such as the generalized hydrodynamic (GH) model (Kaw, Reference Kaw2001, Chakrabarti & Ghosh Reference Chakrabarti and Ghosh2015), the nonlinear quasilocalized charged approximation (QLCA) model (Prince Kumar and Devendra Sharma, 2023, Prince Kumar and Devendra Sharma, 2022) and molecular dynamical (MD) simulations (Kumar, Tiwari & Das, Reference Kumar, Tiwari and Das2017, Tiwari et al. Reference Tiwari, Das, Sen and Kaw2015). These models successfully describe the soliton structures within their respective regimes of applicability. The one-component version of the GH model has been applied to describe how the viscoelasticity of the medium affects the solitons, with the relaxation time
$\tau _{m}$
and the viscosity
$\eta$
as essential parameters (Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). This version of the GH model has a limited scope, preventing it from effectively exploring the wide range of the screening regime of the nonlinear excitations in Yukawa media (Kaw, Reference Kaw2001). The nonlinear QLCA model, however, overcomes this barrier by incorporating the explicit localization of the constituent particles in the formulation (Prince Kumar and Devendra Sharma, 2023, Prince Kumar and Devendra Sharma, 2021). The QLCA was developed as a framework to model the dielectric response and the dispersion of collective modes in strongly coupled liquid-phase plasmas, where the coupling parameter
$(\Gamma \gg 1)$
indicates a highly localized regime. Consequently, this framework is applicable only within the localized domain of systems (Prince Kumar and Devendra Sharma, 2023, Golden & Kalman Reference Golden and Kalman2000). Moreover, investigating the influence of the parameter
$\Gamma$
on solitons in dusty plasmas is interesting, given the limited insights provided by experimental results. The purpose of this paper is to present a description of the dust solitons across a wide range of parametric values using a simple fluid model (SFE) and to compare it with existing models, MD simulations and experimental results.
The paper presents a SFE model (Khrapak & Thomas Reference Khrapak and Thomas2015), supplemented by a suitable equation of state, to characterize solitons across a broad range of parameters
$\Gamma$
and
$\kappa$
. We adopt the practical expression of the internal energy and the pressure, applicable across coupling regime, to calculate the compressibility of the Yukawa medium (Khrapak & Thomas Reference Khrapak and Thomas2015). The formulation covers a broad range of parameters
$\Gamma$
and
$\kappa$
, consistent with the weak screening limit of the nonlinear QLCA and GH models in characterizing the solitons in Yukawa media. The results obtained within the framework of the SFE model also exhibit a quantitative agreement with experimentally measured values of the width and Mach number for various values of the normalized amplitude (Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). Agreement is achieved for lower values of
$\kappa$
, and the characteristics of the solitons are not significantly altered by varying the
$\Gamma$
parameter. It has been observed that the amplitude and width of the soliton in the weak screening limit increases with
$\Gamma$
up to the value
$\Gamma \sim 10$
, beyond this value it remains independent of
$\Gamma$
values. The MD simulations presented in this paper also confirm that the localization starts emerging beyond
$\Gamma \sim 10$
which shows no impact on the solitons in Yukawa media. Therefore, the SFE model can accurately predict the effects of the onset of localization on the nonlinear excitations in Yukawa media. The amplitude and width of the soliton increases and decreases, respectively, with
$\kappa$
values. The SFE model also explores the possibility of forming refractive soliton structures whose intensity increases and decreases with
$\kappa$
and
$\Gamma$
values, respectively.
The SFE model may successfully overcome the limitations of the nonlinear QLCA in the weak coupling regime (Prince Kumar and Devendra Sharma, 2023) and the one-component version of the GH model (Kaw, Reference Kaw2001) in the strong screening limit of the solitons in Yukawa media. However, it is known that the simplistic fluid treatment is applicable to longer wavelengths or low frequencies and becomes irrelevant in the highly localized regime. The fluid model’s limited scope prevents it from accessing relatively shorter collective modes, as its phenomenological equation of state is not applicable in this limit (Khrapak & Thomas Reference Khrapak and Thomas2015). The significant contribution to the formation of the Korteweg-de Vries (KdV) solitons, however, comes from lower spectral modes, which are efficiently captured within the framework of the SFE model. Additionally, the precise practical formulations of thermodynamic quantities enable us to achieve quantitative results and conduct detailed comparisons with outcomes from other approaches. The future scope of the formulation is briefly discussed at the end of the paper.
The structure of the article is as follows. The description of the model equations for the soliton in strongly coupled Yukawa media is presented in § 2. The KdV equation is derived using the fluid equations in § 2.1. The analytical KdV results across coupling regime and their comparison with the existing models are presented in § 3. The comparison with the experimental data, the MD simulation, the nonlinear QLCA model and the GH model are presented in §§ 3.2, 3.3, 3.4 and 3.5, respectively. The simulation on the evolution of the general perturbation is presented in § 3.6. The summary and conclusions of the study are presented in § 4.
2. Simple fluid equations with an equation of state for Yukawa fluids: the SFE model
The description of long-wavelength collective excitations in a strongly coupled Yukawa fluid can obtained using the fluid equations that are supplemented with appropriate modified thermodynamic quantities. The momentum and continuity equation for a charged dust fluid are (Khrapak & Thomas Reference Khrapak and Thomas2015)
\begin{eqnarray} \begin{split} \frac {\partial \textbf{u}_{\textrm{d}} }{\partial t} + (\textbf{u}_{\textrm{d}} \cdot \nabla ) \textbf{u}_{\textrm{d}} = \frac {Q}{m_{\textrm{d}}}\textbf{E} - \frac {1}{m_{d} n_{d}} \nabla P_{d}, \end{split} \end{eqnarray}
\begin{equation} \frac {\partial n_{d}}{\partial t} + \nabla \cdot (n_{d} \textbf {u}_{d}) = 0. \end{equation}
The adiabatic compressiblilty of the medium can be related to isothermal compressibility by using expression given as
\begin{equation} \left (\frac {\partial P }{\partial n_{d}}\right )_{S} = \gamma \left (\frac {\partial P }{\partial n_{d}}\right )_{T} \end{equation}
where S is system entropy and
$\gamma$
=
$C_{P}/C_{V}$
is the adiabatic index. Using above expression, (2.1) can therefore be written as
\begin{equation} \frac {\partial \textbf{u}_{\textrm{d}} }{\partial t} + (\textbf{u}_{\textrm{d}} \cdot \nabla ) \textbf{u}_{\textrm{d}} = \frac {Q}{m_{\textrm{d}}}\textbf{E} - {V_{th}^2 \gamma \alpha } \frac {\nabla n_{d}}{ n_{d}}, \end{equation}
where
$V_{th}$
=
$\sqrt {T_{d}/m_{d}}$
is the thermal velocity of dust particles,
$T_d$
is the dust-thermal energy,
$Q = -Ze$
is the dust charge, the electric field
$\mathbf {E} = -\nabla \phi$
and
$\alpha$
=
$\left (1/T_{d}\right )\left ({\partial P }/{\partial n_{d}}\right )_{T}$
is the isothermal compressibility modulus.
Upon normalization, (2.4) takes the form
\begin{equation} \frac {\partial \textbf{u}_{\textrm{d}} }{\partial t} + (\textbf{u}_{\textrm{d}} \cdot \nabla ) \textbf{u}_{\textrm{d}} = \mu {\nabla \phi } - \frac{\gamma \alpha }{3\Gamma } \frac {\nabla n_{d}}{n_{d}}, \end{equation}
and the normalized Poisson equation becomes
\begin{equation} \nabla ^2 \phi = \frac {1}{\mu }\left [n_{d}+n_{e}-n_{i}\right ], \end{equation}
where
$n_e = \delta _{e} \exp \left ({\sigma _{e} \phi }\right )$
, and
$n_i = \delta _{i} \exp \left ({-\sigma _{i}\phi }\right )$
. We have the dimensionless parameters
$\mu ={Z_{d} T_{d}}/({m_{d} a^{2}\omega ^{2}_{pd}})$
,
$\delta _{e}=n_{e0}/Z_{d}n_{d0}$
,
$\delta _{i}=n_{i0}/Z_{d}n_{d0}$
and
$\sigma _{i,e}=T_{d}/T_{i,e}$
. The equilibrium dust density
$n_{d0}$
, the ratio
$T_{d}/e$
, dust acoustic frequency
$\omega _{\textrm{pd}} = \sqrt {4\pi Q^2n_{d0}/m_{d}}$
and mean dust separation
$a =\left (4 \pi n_{d0}/3\right )^{-1/3}$
are used as normalizations for the density, potential, time and length, respectively. Equations (2.5)–(2.7) along with the continuity (2.2) constitute a nonlinear model as the convective nonlinearity in the second term and the nonlinear second term in right-hand side of (2.5) are retained. The value of the coefficient
$\gamma \alpha$
is given as (Khrapak & Thomas Reference Khrapak and Thomas2015, Khrapak & Thomas Reference Khrapak and Thomas2015)
\begin{equation} \gamma \alpha = \alpha + \frac {\left (p-\Gamma \left (\partial p/\partial \Gamma \right )\right )^2}{u-\Gamma \left (\left (\partial p/\partial \Gamma \right )\right )} \end{equation}
where
$u$
,
$p$
and
$\alpha$
account for particle–particle correlation and plasma-related effects. The
$u(\Gamma, \kappa )$
,
$p(\Gamma, \kappa )$
and
$\alpha (\Gamma, \kappa )$
, are the system excess energy, pressure and isothermal compressibility modulus (Khrapak & Thomas Reference Khrapak and Thomas2015). The expressions for these parameters are presented in appendix A. The model equations presented here are first used to drive the KdV equation to study soliton structures in Yukawa media across various coupling regimes. This is followed by the analysis of the results and their validation with experimental data, MD simulation, the GH model and the QLCA model. For simplicity, from now on, let
$\alpha = \frac{\gamma \alpha}{3\Gamma}$
.
2.1. Derivation of the KdV equation for a strongly coupled Yukawa fluid
In order to obtain the KdV equation (Davidson, Reference Davidson2012) for this system, we first introduce slow variables
$\zeta$
and
$\tau$
, given by
\begin{equation} \zeta = \epsilon ^{1/2}(x-v_{0}t),\,\,\,\,\tau = \epsilon ^{3/2}t, \end{equation}
where
$\epsilon$
is a smallness parameter measuring the weakness of the perturbation and
$V_{0}$
represent the phase velocity of the dust acoustic wave (DAW). In terms of
$\zeta$
and
$\tau$
the equations become
\begin{equation} \epsilon ^{3/2} \frac {\partial n_{d}}{\partial \tau } - V_{0} \epsilon ^{1/2} \frac {\partial n_{d}}{\partial \zeta }+ \epsilon ^{1/2} \frac {\partial n_{d} u_{d}}{\partial \zeta } = 0, \end{equation}
\begin{eqnarray} \begin{split} \epsilon ^{3/2} \frac {\partial u_{d}}{\partial \tau } - V_{0} \epsilon ^{1/2} \frac {\partial u_{d}}{\partial \zeta }+ \epsilon ^{1/2} u_{d}\frac {\partial u_{d}}{\partial \zeta } = \mu \epsilon ^{1/2} \frac {\partial \phi }{\partial \zeta } \\ - \frac {\alpha }{n_{d}} \frac {\partial n_{d}}{\partial \zeta } \end{split} \end{eqnarray}
and
\begin{eqnarray} \begin{split} \epsilon ^{3/2} \frac {\partial ^2 \phi }{\partial \zeta ^2} & = \frac {1}{\mu } \Bigg \{ \delta _{e} \left [ 1+\sigma _{e} \phi + \frac {1}{2} \sigma ^2_{e} \phi ^2 + ..\right ] \\& \quad - \delta _{i} \left [ 1-\sigma _{i}\phi + \frac {1}{2} \sigma ^2_{i}\phi ^2 + ..\right ] + n_{d}\Bigg \}. \end{split} \end{eqnarray}
We can now expand the variables
$n_{d}$
,
$u_{d}$
and
$\phi$
in the power series of
$\epsilon$
,
\begin{eqnarray} \begin{split} n_{d} = 1 + \epsilon n^{(1)}_{d} + \epsilon ^{2} n^{(2)}_{d} + \ldots \ldots \ldots . \\ u_{d} = \epsilon u^{(1)}_{d} + \epsilon ^{2} u^{(2)}_{d} + \ldots \ldots \ldots . \\ \phi = \epsilon \phi ^{(1)} + \epsilon ^{2} \phi ^{(2)} + \ldots \ldots \ldots . \end{split} \end{eqnarray}
Substituting (2.12) into (2.9), (2.10), (2.11) and equating coefficients of
$\epsilon ^{3/2}$
, we get, to lowest order,
\begin{equation} -V_{0}\frac {\partial n^{(1)}_d}{\partial \zeta } + \frac {\partial u^{(1)}_d}{\partial \zeta } = 0, \end{equation}
\begin{equation} -V_{0}\frac {\partial u^{(1)}_d}{\partial \zeta } + \alpha \frac {\partial n^{(1)}_d}{\partial \zeta } - \mu \frac {\partial \phi ^{(1)}}{\partial \zeta } = 0 \end{equation}
and
\begin{equation} -\frac {h_{1}}{\mu } \phi - \frac {1}{\mu } n^{(1)}_{d}=0. \end{equation}
After integrating and rearranging terms, the following linear expressions are obtained:
\begin{equation} u^{(1)}_{d} = - \frac {\mu V_{0}}{(V^2_{0}-\alpha )} \phi ^{(1)}, \end{equation}
\begin{equation} n^{(1)}_{d} = - \frac {\mu }{(V^2_{0}-\alpha )} \phi ^{(1)} \end{equation}
and
\begin{equation} V_{0} = \left ( \frac {\mu }{h_1} + \alpha \right )^{1/2}, \end{equation}
where
$h_{1}$
=
$(T_{d}\delta _{e}/T_{e} + T_{d}\delta _{i}/T_{i})$
and
$\kappa ^{2}$
=
$\frac {h_{1}}{\mu }$
=
$\frac {a^2}{\lambda ^2_{D}}$
. Equation (2.18) describes how the phase velocity of the DAW changes with
$\alpha$
.
The KdV equation derived for strongly coupled Yukawa fluids using (2.5)–(2.7) and (2.2) is given as
\begin{eqnarray} \begin{split} \frac {\partial \phi ^{(1)}}{\partial \tau } + A \phi ^{(1)}\frac {\partial \phi ^{(1)}}{\partial \zeta } + B \frac {\partial ^{3} \phi ^{(1)}}{\partial \zeta ^{3}} = 0, \end{split} \end{eqnarray}
where the nonlinear coefficient
$A$
and the dispersion coefficient
$B$
are given by
\begin{eqnarray} \begin{split} A = \left [ \frac {\mu \alpha }{2 V_{0} ( V^2_{0} - \alpha )} - \frac {3 \mu V_{0}}{2 ( V^2_{0} - \alpha )} + \frac {(V^2_{0} -\alpha ) h_{2}}{2 V_{0} h_{1}}\right ], \end{split} \end{eqnarray}
\begin{eqnarray} \begin{split} B = \frac {(V^2_{0} - \alpha )\mu }{2 V_{0} h_1}, \end{split} \end{eqnarray}
with
$h_{2}$
=
$\left [\delta _{i}(T_d/T_i)^{2}) -\delta _{e} (T_d/T_e)^{2}\right ]$
.
Equation (2.19) can be solved by separating variables, resulting in a solution in the laboratory frame,
\begin{eqnarray} \begin{split} \phi (x,t) = \phi _{m} \text {sech}^{2}\left [\frac {z}{\Delta }\right ], \end{split} \end{eqnarray}
where
\begin{eqnarray} \begin{split} \phi _{m} = \frac {3U_{0}}{A}\,\,\textrm {and}\,\,\Delta = \sqrt \frac {4B}{U_{0}}, \end{split} \end{eqnarray}
where
$\phi _{m}$
and
$\Delta$
represent the amplitude and width of the soliton, respectively. Here,
$z$
denotes a coordinate in the laboratory frame, and
$U_{0}$
is the normalized velocity of the solitary wave.
3. Analytical results and their comparison with other approaches
3.1. Analytical KdV solutions using the SFE model
Figure 1. The amplitude (
$\phi _m$
) of the soliton with
$U_{0}$
is presented in (a) for different values of
$\Gamma$
while keeping
$\kappa = 0.5$
. The amplitude (
$\phi _m$
) of the soliton with
$U_{0}$
is presented in (b) for different values of
$\kappa$
while keeping
$\Gamma = 100$
.
Figure 2. The figure illustrates the equilibrium radial distribution function (RDF) various values of the coupling parameter
$\Gamma$
. Peaks in the RDF begin to appear at
$\Gamma \sim 10$
and are most prominent around
$\Gamma \sim 100$
. All results are plotted with a fixed screening parameter of
$\kappa = 0.5$
.
This section presents the variation of the width and amplitude of the solitary structures across a broad range of the
$\Gamma$
and
$\kappa$
parameters. The amplitude
$\phi _m$
and width
$\Delta$
of the solitary structures can be calculated using (2.23). The parameters
$\phi _m$
and
$\Delta$
implicitly depend on
$\Gamma$
and
$\kappa$
through the isothermal compressibility
$\alpha (\Gamma, \kappa )$
, which influences the KdV coefficients
$A$
and
$B$
presented in (2.20) and (2.21), respectively. The variation of the amplitude of the solitary structures is presented in figures 1(a) and 1(b) for different values of
$\Gamma$
and
$\kappa$
, respectively. The value of parameters
$\Gamma$
and
$\kappa$
are considered to characterize the solitary structures in the weak to moderate coupling regime of the system. The variation of
$\phi$
with
$U_{0}$
for a set of
$\Gamma$
values is presented in figure 1(a), with the value of
$\kappa$
fixed at
$0.5$
. It has been observed that the amplitude increases with
$U_{0}$
for the fixed values of
$\Gamma$
and
$\kappa =0.5$
. As can be seen in figure 1(a), the amplitude of the solitary structures also increase with
$\Gamma$
values, however, the increment is more pronounced only at lower values of
$\Gamma$
. In figure 1(a), each colour represents a different value of
$\Gamma$
: blue for
$\Gamma = 0.01$
; red dotted for
$\Gamma = 0.1$
; yellow for
$\Gamma = 1.0$
; purple for
$\Gamma = 10$
; green circles for
$\Gamma = 100$
. As the value of
$\Gamma$
increases, the increment in the amplitude decreases. This dependency is observed up to
$\Gamma = 10$
, beyond which the amplitude remains independent of
$\Gamma$
. It is evident from the overlap of the purple line (for
$\Gamma$
= 10) and the green circles (for
$\Gamma = 100$
) in the figure 1(a). It has been observed that the amplitude is highly sensitive to
$\Gamma$
at relatively weak coupling regime and higher values of
$U_{0}$
. Interestingly, the peak in the RDF start emerging after
$\Gamma \gt 1$
, as illustrated in figure 2, confirms that the localization of the constituent particles becomes significant for
$\Gamma \gt 1$
. It can be concluded that the caging of the constituent particles in the potential landscapes does not significantly contribute to the formation of the solitary structures in Yukawa systems. The formation of the solitary structures in this quasilocalized limit will be discussed within the QLCA model further in the upcoming section.
The variation of
$\phi _m$
with
$U_{0}$
for a set of
$\kappa$
values is presented in figure 1(b), with
$\Gamma$
fixed at 100. It has been observed that the amplitude increases with
$U_{0}$
for the fixed values of
$\kappa$
and
$\Gamma =100$
. As depicted in figure 1(b), the amplitude of the solitary structures increases with
$\kappa$
values, and the increment being pronounced across all values of
$\kappa$
. In figure 1(b), each colour represents a different value of
$\kappa$
: blue for
$\kappa = 0.5$
; red dotted for
$\kappa = 1.1$
; yellow for
$\kappa = 1.7$
; purple for
$\kappa = 2.3$
. This occurs because as
$ \kappa$
increases, the interaction among particles weakens, making the interaction between neighbouring particles more significant than the collective interactions. We will present a comparison of these observations with the nonlinear QLCA model in the upcoming section.
Figure 3. The width (
$\Delta$
) of the soliton with
$U_{0}$
is presented in (a) for different values of
$\Gamma$
while keeping
$\kappa = 0.5$
. The width (
$\Delta$
) of the soliton with
$U_{0}$
is presented in (b) for different values of
$\kappa$
while keeping
$\Gamma = 100$
.
The variation of
$\Delta$
with
$U_{0}$
for a set of
$\Gamma$
values is presented in figure 3(a), with
$\kappa$
fixed at
$0.5$
. It has been observed that the width decreases with
$U_{0}$
for the fixed values of
$\Gamma$
and
$\kappa =0.5$
. The width of the solitary structures increase with
$\Gamma$
values, however, the increment is more pronounced only at lower values of
$\Gamma$
.
As the value of
$\Gamma$
increases, the increment in the width decreases. This dependency is observed up to
$\Gamma = 10$
, beyond which the width remains independent of
$\Gamma$
. It is evident from the overlap of the purple line (for
$\Gamma = 10$
) and the green circles (for
$\Gamma = 100$
) in the figure 3(a). Similar to the cases of amplitude, the width is also highly sensitive to
$\Gamma$
only at relatively weak coupling regime and at higher values of
$U_{0}$
. The variation of
$\Delta$
with
$U_{0}$
for a set of
$\kappa$
values is presented in figure 3(b), with
$\Gamma$
fixed at
$100$
. The width decreases with
$\kappa$
, however, the decrement is more pronounced only at lower values of
$\Gamma$
. Solitons are stable, localized wave packets that occur when the nonlinearity, resulting from interactions between dust particles, balances with the dispersion from the collective response of the dusty plasma. As the dust temperature increases, or equivalently as the coupling parameter
$\Gamma$
decreases, this balance is disrupted because the effects of nonlinearity weaken. This disruption leads to the formation of broader and shorter solitons.
Figure 4. The width and Mach number are plotted with the soliton amplitude in (a) and (b), respectively, for
$\kappa = 0.3$
and
$\Gamma = 100$
.
3.2. Experimental validations of the SFE model
This section is dedicated to providing experimental validation of the SFE model. The variation of the Mach number and the width
$\Delta$
of the soliton structures for the normalized amplitude is presented in figure 4 under the same experimental conditions (Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). The width of the soliton presented in figure 4(a) decreases with the normalized amplitude of the soliton. The Mach number presented in figure 4(b) increases with the normalized amplitude of the soliton. These analytical results show a good quantitative agreement with the experimentally measured values of the width and the Mach number with normalized amplitude (see Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). Agreement is achieved for lower values of
$\kappa$
, and the characteristics of the soliton are not significantly altered by varying the
$\Gamma$
parameter.
3.3. Validations with MD simulations
Figure 5. The snapshot of the solitary waves at time, induced by an electric field perturbation with a magnitude of
$E = 25.40$
, for different values of
$\Gamma$
. The solitary pulse, depicted in red and green and blue dotted, emerges at
$\Gamma = 10$
,
$\Gamma = 50$
and
$\Gamma = 100$
, respectively, with a fixed screening parameter of
$\kappa = 0.5$
.
In this section, the MD simulations are conducted to validate the theoretically predicted results across a range of
$\Gamma$
values. The soliton structures shown in figure 5 are excited by applying an electric field within a small region of the rectangular simulation box. Further details regarding the simulation parameters and methodology can be referenced in our previous work (Prince Kumar and Devendra Sharma, 2024). Figure 5 represents the soliton-like structures for the various values of
$\Gamma$
and a constant
$\kappa = 0.5$
. The red, green and dotted blue lines represent the soliton profiles for
$\Gamma$
= 10, 50 and 100, respectively. It can be seen from figure 5 that the characteristic properties of the solitons remain independent of
$\Gamma$
. These results are in close quantitative agreement with the theoretical predictions shown in figures 1 and 3. They predict that the amplitude and width of the solitons remain independent of
$\Gamma$
beyond
$\Gamma \sim 10$
(the onset of localization). Therefore, the theoretical model accurately predicts the onset of localization and its effects on the nonlinear excitations in Yukawa media.
3.4. Comparison with the nonlinear QLCA model
In this section, we present a brief comparison between the SFE model and the nonlinear QLCA model across various sets of
$\Gamma$
and
$\kappa$
parameters. The basic equations for the nonlinear QLCA model are presented in appendix B. The QLCA model, due to its construction, remains applicable to the highly localized regime, whereas the SFE model also tends to cover a relatively weak coupling regime. The fluid model’s limited scope prevents it from accessing relatively shorter collective modes, as its phenomenological equation of state is not applicable in this limit. The contribution of relatively shorter wavelengths to the formation of soliton structures becomes significant in the stronger screening limit (
$\kappa \gt 1$
), a phenomenon successfully described by the nonlinear QLCA model. Figure 6 illustrates the solitons derived from the simple fluid and the nonlinear QLCA model for various values of
$\kappa$
. The results plotted for
$\kappa$
=
$0.3$
and
$1.0$
in figure 6(a) and 6(b), respectively, show that the SFE model agrees with the observations of the nonlinear QLCA model in the weak screening limit. The soliton structures are derived within the nonlinear QLCA framework utilizing the analytical form of the D-matrix, which is calculated using the isothermal compressibility as outlined in (B.4). However, the description of the relatively high screening regime of nonlinear excitations requires a more sophisticated form of the D-matrix cable of accommodating the relatively higher modes in the formulation. Moreover, the significance contribution to the formation of the KdV solitons comes from lower spectral modes that are efficiently captured within the framework of the SFE model. The QLCA results confirms the applicability of the SFE model in describing the weak to moderate screening regime of the solitons in Yukawa media.
Figure 6. The soliton profiles calculated from the SFE model and QLCA for
$\kappa = 0.3$
and
$\kappa =1.0$
are presented in (a) and (b), respectively. The value of the parameter
$ \Gamma$
is considered to remain within the quasilocalized regime of the medium.
3.5. Comparsion with the GH model
In this section, we present a brief comparison between the SFE model and the GH model for describing the solitons in Yukawa media. A brief introduction to the KdV equations derived within the GH framework is provided in appendix C. The KdV coefficients are the function of the system excess energy via the relaxation time (
$\tau _{m}$
) and the coefficient of viscosity (
$\eta$
). Since the excess energy u(
$\Gamma$
) of the medium remains independent of
$\kappa$
, this version of the model has a limited scope, preventing it from effectively exploring the wide range of the screening regime of the nonlinear excitations in Yukawa media. However, the SFE model has accessibility to explore the relatively high screening regime of the solitons in Yukawa fluids, as the internal energy and the compressibility in the model are the explicit functions of the
$\kappa$
(see (A.1) and (A.5)). The Mach number and the width
$\Delta$
of the soliton structures for the normalized amplitude are depicted in figure 4. These results can also be reproduced using the GH model for a specific set of experimental parameters (Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). These observations further confirm the efficacy of the SFE model in describing the nonlinear excitations in strongly coupled Yukawa systems. Similar to the case of the SFE model, we also observe from the GH model that the characteristics of the soliton structures do not depend on the
$\Gamma$
value. However, the GH model proves more accurate in describing the effects of shear waves in the medium, an area where the SFE model falls short.
3.6. Numerical simulations with the general perturbations
To simulate the evolution of the general perturbations governed by (2.5)–(2.7) and (2.2), we employ a pseudospectral technique utilizing the fast Fourier transform library (Frigo, May Reference Frigo1999). These discretization schemes are chosen to adhere to the Courant–Friedrichs–Lewy condition (Russell, Reference Russell1989). For time integration, we employ the Adams–Bashforth method (Durran, Reference Durran1991). The aliasing effects induced by nonlinear terms are mitigated using the well-established two-thirds rule proposed by Orszag (Patterson & Orszag Reference Patterson and Orszag1971). We apply an initial Gaussian pulse in the medium for a wide range of
$\Gamma$
and
$\kappa$
values. The mathematical form of the profile is written as
\begin{equation} n_{d} = n_{0} \exp \left [-\left (\frac {z-z_{0}}{\Delta }\right )^2\right ], \end{equation}
where
$\Delta$
and
$n_{0}$
are the width and amplitude of the perturbation. The initial density perturbation, depicted in figure 7(a) with a blue colour for
$\kappa = 2.0$
, disintegrates into positive and negative density profiles travelling in opposite directions. The snapshot of the profile at
$t\omega _{pd} = 150$
is shown in yellow in figure 7(b). To investigate the effects of
$\kappa$
, we further evolve the initial perturbation with
$\kappa = 2.5$
and present the snapshot of the density at
$t = 150 \omega _{pd}$
in figure 7(a) with the green colour. The increment in the intensity of the refractive soliton with
$\kappa$
is also confirmed with the MD simulation results (Donkó et al. Reference Donkó, Hartmann, Masheyeva and Dzhumagulova2020). Now, we are interested in exploring the effects of
$\Gamma$
on the evolution of the general density perturbations. Therefore, the snapshot of the disintegrated profiles is plotted in figure 7(b) for different values of
$\Gamma$
. The blue, red and green colours represent the profile at
$t = 50 \omega _{pd}^{-1}$
for
$\Gamma = 1.0$
, t = 50
$\omega _{pd}^{-1}$
for
$\Gamma = 10$
and
$t = 50 \omega _{pd}^{-1}$
for
$\Gamma = 50$
, respectively. This shows that the intensity of rarefactive solitons decreases with
$\Gamma$
, and no rarefactive solitons are observed beyond
$\Gamma = 1$
at
$\kappa = 3.0$
.
Figure 7. The figure illustrates the progression of an initial gaussian density perturbation characterized by a width
$\Delta = 10$
and an amplitude
$A = 0.05$
. Panels (a) and (b) correspond to different values of
$\kappa$
and
$\Gamma$
, respectively.
4. Summary and conclusions
We have introduced the SFE model to describe the nonlinear excitations in strongly coupled Yukawa fluids across a broad spectrum of
$\Gamma$
and
$\kappa$
values. The equation of state of the medium is obtained using the practical expressions for the internal energy and pressure, which are applicable across a wide range of the coupling regime. The formulation describes the solitons across a wide spectrum of parameters
$\Gamma$
and
$\kappa$
values, encompassing the respective domains of applicability of the nonlinear QLCA and GH models in characterizing the solitons in Yukawa media. The formulation also reproduces the experimentally measured values of the width and Mach number for various values of the normalized amplitude (Sharma, Boruah & Bailung, Reference Sharma, Boruah and Bailung2014). It has been observed that the amplitude and width of the soliton in weak coupling limit (no-localization) increases with
$\Gamma$
up to the value
$\Gamma \sim 10$
, beyond this value it remains independent to
$\Gamma$
values. The MD simulations confirm that the localization starts emerging beyond
$\Gamma \sim 10$
which shows not impact on the solitons in Yukawa media.
The SFE model may successfully overcome the limitations of the nonlinear QLCA in the weak coupling regime and the one component plasma version GH model in the strong screening limit of solitons in Yukawa media. It is known that the simplistic fluid treatment (Prince Kumar and Devendra Sharma, 2020) is applicable to longer wavelengths or low frequencies and becomes irrelevant in the highly localized regime. The fluid model’s limited scope prevents it from accessing relatively shorter collective modes, as its phenomenological equation of state is not applicable in this limit. However, the significant contribution to the formation of the KdV solitons comes from lower spectral modes, which are efficiently captured within the framework of the SFE model. Additionally, the precise practical formulations of thermodynamic quantities enable us to achieve quantitative results and conduct detailed comparisons with outcomes from other approaches. The SFE model presents a distinctive opportunity to precisely quantify the longitudinal nonlinear excitations and their instabilities of Yukawa or dusty plasma systems (Sandip Dalui, Prince Kumar, and Devendra Sharma, 2023). This is facilitated by the explicit dependency of the compressibility, pressure, adiabatic index and internal energy of the system on
$\Gamma$
and
$\kappa$
. One of the example is modulational instability which is likely to occur in frequency ranges where the dispersion relation of the DAW exhibits anomalous behaviour, such as regions of negative dispersion. In a specific range of
$\Gamma$
and
$\kappa$
, the compressibility changes its sign to negative, resulting in a negative dispersion relation at a certain
$k$
value. As a consequence, the group velocity approaches zero at a specific value of
$k$
and subsequently becomes negative. In this context, it would be interesting to investigate how variations in
$\Gamma$
and
$\kappa$
influence the modulational instability of the dust acoustic modes.
The present work can be of finite interest to the complex (dusty) plasma and nonlinear plasma waves communities. It offers valuable insights into the underlying physics of nonlinear excitations, which can significantly benefit researchers in this field. This is achieved through its construction, which includes explicit expressions for thermodynamic quantities that account for both particle–particle correlations and plasma-related effects. For example, while the adiabatic index
$\gamma$
shows a discontinuity at moderate coupling (Khrapak & Thomas Reference Khrapak and Thomas2015), this does not impact the dust solitary structures. The structures are governed by the product
$\gamma \alpha$
, which remains finite, as compressibility vanishes in this regime. A more specific analysis will be conducted in future work.
Acknowledgements
The simulations are performed on the Antya cluster at the Institute for Plasma Research (IPR).
Editor Edward Thomas, Jr. thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Thermodynamic functions for strongly coupled Yukawa systems
The main objective is to calculate the isothermal compressibility
$\alpha$
of a strongly coupled Yukawa medium. The practical expressions of the thermodynamic quantities for strongly coupled Yukawa systems has been derived using the ion spherical model assumptions Khrapak et al. (Reference Khrapak, Khrapak, Ivlev and Thomas2014). The expression for the internal energy parameter is written as
\begin{equation} \begin{split} u_{\text {}}(\kappa, \Gamma ) = \frac {3}{2} + \epsilon + \left [\frac {\kappa (\kappa + 1)\Gamma }{(\kappa + 1) + (\kappa - 1)e^{2\kappa }}\right ] \\+ \delta \left (\frac {\Gamma }{\Gamma _m}\right )^{2/5}-\frac {3\Gamma }{2\kappa ^2} - \frac {\kappa \Gamma }{2}, \end{split} \end{equation}
where the last two terms correspond to the plasma-related contribution to the internal energy of the medium. The explicit expression for the compressibility factor is given as Khrapak & Thomas (Reference Khrapak and Thomas2015)
\begin{equation} \begin{split} Z(\kappa, \Gamma ) = \left (1 + \frac {\epsilon }{3}\right ) + \frac {\Gamma \kappa ^4}{6[\kappa \cosh (\kappa ) - \sinh (\kappa )]^2} \\ + \frac {\delta }{3} \left (\frac {\Gamma }{\Gamma _m}\right )^{2/5} f_Z(\beta \kappa ), \end{split} \end{equation}
where
\begin{equation} f_Z(x) = \frac {x^3 + x^2 + 2x + 2}{x^2 + 2x + 2}. \end{equation}
The isothermal compressibility modulus is related to the compressibility factor via
\begin{equation} \alpha = Z + \frac {\Gamma }{3} \frac {\partial Z}{\partial \Gamma } - \frac {\kappa }{3} \frac {\partial Z}{\partial \kappa }. \end{equation}
This yields
\begin{equation} \begin{split} \alpha (\kappa, \Gamma ) = \left (1 + \frac {\epsilon }{3}\right ) + \frac {\Gamma \kappa ^6 \sinh (\kappa )}{9[\kappa \cosh (\kappa ) - \sinh (\kappa )]^3} \\ + \frac {\delta }{45} \left (\frac {\Gamma }{\Gamma _m}\right )^{2/5} f_\alpha (\beta \kappa ), \end{split} \end{equation}
where
\begin{equation} f_\alpha (x) = \frac {2x^6 + 14x^5 + 35x^4 + 76x^3 + 136x^2 + 136x + 68}{(x^2 + 2x + 2)^2}. \end{equation}
The pressure of the medium can be expressed in term of the compressibility factor
$Z(\kappa, \Gamma )$
as,
$p(\kappa, \Gamma ) = Z(\kappa, \Gamma )+\left (3\Gamma / 2\kappa ^2-1\right )$
. The coupling parameter at fluid–solid phase transition is
$\Gamma _m \sim \left [172 \exp (\beta \kappa )/\left (1 + \beta \kappa + \frac {1}{2} \beta ^2 \kappa ^2\right )\right ]$
, and the value of parameters
$\epsilon = -0.1$
,
$\beta = 1.614$
and
$\delta = 3.2$
are considered for the present analysis.
Appendix B. The nonlinear QLCA model for Yukawa fluids
The momentum conservation equation retaining localizations via QLCA basis is given as Prince Kumar and Devendra Sharma (2023)
\begin{equation} \frac {\partial {u}_{dx} }{\partial t} + {u}_{dx}\frac {\partial {u}_{dx} }{\partial x} = \mu \frac {\partial \phi }{\partial x} -\tilde {\alpha } \frac {1}{n_{dx}}\frac {\partial n_{dx}}{\partial x}, \end{equation}
which is supplemented by the continuity
\begin{equation} \frac {\partial n_{dx}}{\partial t} + \frac {\partial }{\partial x} (n_{dx} u_{dx}) = 0, \end{equation}
and the Poisson equation
\begin{equation} \frac {\partial ^2\phi }{\partial x^2} = \frac {1}{\mu }\left [n_{d}+n_{e}-n_{i}\right ], \end{equation}
respectively. Equations (B.1)–(B.3) form a nonlinear QLCA model. The analytical form of the isothermal compressibility factor within the QLCA basis is given by
\begin{equation} \alpha (\kappa ) = - 0.0799 - 0.0046 \kappa ^2 + 0.0016 \kappa ^4 \end{equation}
Furthermore, a more sophisticated form of the D-matrix can be incorporated via a pseudospectral technique, as discussed in Prince Kumar and Devendra Sharma (2023)
Appendix C. The KdV equation from the GH model
The GH model was adopted by the dusty plasma community to study the effects of the viscoelastic nature of the medium on its collective excitations. The viscoelastic contribution incorporated via the relaxation time (
$\tau _{m}$
) shows the finite effects on the linear and collective excitations of the medium. The details about the model equations can be found in Kaw & Sen (Reference Kaw and Sen1998). As a particular interest here to analysis the KdV equations derive within the framework of the GH model, can be written as Sharma, Boruah & Bailung (Reference Sharma, Boruah and Bailung2014)
\begin{eqnarray} \begin{split} \frac {\partial n^{(1)}}{\partial \tau } + A n^{(1)}\frac {\partial n^{(1)}}{\partial \zeta } + B \frac {\partial ^{3} n^{(1)}}{\partial \zeta ^{3}} = 0, \end{split} \end{eqnarray}
where the nonlinear coefficient
$A$
and the dispersion coefficient
$B$
are given by
\begin{eqnarray} \begin{split} A = \frac {2\alpha \lambda +\left [\beta \left (\mu _e \sigma _e^2-\mu _i\right )\lambda /\beta ^2\right ]-\lambda ^3\tau _m}{\left (\alpha -2\lambda ^2\tau _m+\tau _m\right )}, \end{split} \end{eqnarray}
\begin{eqnarray} \begin{split} B = \frac {\alpha \lambda }{\left (\alpha -2\lambda ^2\tau _m+\tau _m\right )}, \end{split} \end{eqnarray}
where
$\alpha = \eta ^{*}-\lambda ^2 \tau _m$
,
$\beta = \mu _e\sigma _i+ \mu _i$
. The parameter
$\eta ^{*}$
is the viscosity coefficient whose empirical analytical expression can be written as
$\eta = a (\Gamma _{m}/\Gamma ) + b (\Gamma /\Gamma _{m}) +c$
, where the table for the unknown coefficients is given in Saigo & Hamaguchi (Reference Saigo and Hamaguchi2002). The memory relation time
$\tau _{m} = 3\,\eta ^{*}\Gamma \left [1-\gamma \mu +0.266u(\Gamma )\right ]^{-1}$
follows the trend of the viscosity parameter
$\eta ^{*}$
Chakrabarti & Ghosh (Reference Chakrabarti and Ghosh2015). The compressibility
$\mu$
is calculated from the excess energy for one component plasma (
$\kappa$
=0) for the range
$1\lt \Gamma \lt 200$
. Therefore, the scope of the presented form of the GH model is limited in describing the relative strong screening regime of the medium.
Open access
