Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T08:42:47.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-sustaining sound in collisionless, high-β plasma

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  09 November 2020

M. W. Kunz Open the ORCID record for M. W. Kunz [Opens in a new window] ,
J. Squire Open the ORCID record for J. Squire [Opens in a new window] ,
A. A. Schekochihin Open the ORCID record for A. A. Schekochihin [Opens in a new window]  and
E. Quataert
M. W. Kunz*
Affiliation:
Department of Astrophysical Sciences, Princeton University, Peyton Hall, Princeton, NJ08544, USA Princeton Plasma Physics Laboratory, PO Box 451, Princeton, NJ08543, USA
J. Squire
Affiliation:
Department of Physics, University of Otago, 730 Cumberland St, North Dunedin, Dunedin9016, New Zealand
A. A. Schekochihin
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, Clarendon Laboratory, University of Oxford, Parks Road, OxfordOX1 3PU, UK Merton College, Merton Street, OxfordOX1 4JD, UK
E. Quataert
Affiliation:
Department of Astrophysical Sciences, Princeton University, Peyton Hall, Princeton, NJ08544, USA Department of Astronomy and Theoretical Astrophysics Center, University of California, Berkeley, CA94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

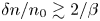Using analytical theory and hybrid-kinetic numerical simulations, we demonstrate that, in a collisionless plasma, long-wavelength ion-acoustic waves (IAWs) with amplitudes $\delta n/n_0 \gtrsim 2/\beta$ (where 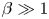$\beta \gg {1}$ is the ratio of thermal to magnetic pressure) generate sufficient pressure anisotropy to destabilize the plasma to firehose and mirror instabilities. These kinetic instabilities grow rapidly to reduce the pressure anisotropy by pitch-angle scattering and trapping particles, respectively, thereby impeding the maintenance of Landau resonances that enable such waves’ otherwise potent collisionless damping. The result is wave dynamics that evince a weakly collisional plasma: the ion distribution function is near-Maxwellian, the field-parallel flow of heat resembles its Braginskii form (except in regions where large-amplitude magnetic mirrors strongly suppress particle transport), and the relations between various thermodynamic quantities are more ‘fluid-like’ than kinetic. A nonlinear fluctuation–dissipation relation for self-sustaining IAWs is obtained by solving a plasma-kinetic Langevin problem, which demonstrates suppressed damping, enhanced fluctuation levels and weakly collisional thermodynamics when IAWs with 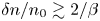$\delta n/n_0 \gtrsim 2/\beta$ are stochastically driven. We investigate how our results depend upon the scale separation between the wavelength of the IAW and the Larmor radius of the ions, and discuss briefly their implications for our understanding of turbulence and transport in the solar wind and the intracluster medium of galaxy clusters.

Keywords

astrophysical plasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 6 , December 2020 , 905860603
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balbus, S. A. 2000 Stability, instability, and ‘backward’ transport in stratified fluids. Astrophys. J. 534, 420–427.CrossRefGoogle Scholar
Balbus, S. A. 2001 Convective and rotational stability of a dilute plasma. Astrophys. J. 562, 909–917.CrossRefGoogle Scholar
Balbus, S. A. 2004 Viscous shear instability in weakly magnetized, dilute plasmas. Astrophys. J. 616, 857–864.CrossRefGoogle Scholar
Bale, S. D., Kasper, J. C., Howes, G. G., Quataert, E., Salem, C. & Sundkvist, D. 2009 Magnetic fluctuation power near proton temperature anisotropy instability thresholds in the solar wind. Phys. Rev. Lett. 103 (21), 211101.CrossRefGoogle ScholarPubMed
Bambic, C. J. & Reynolds, C. S. 2019 Efficient production of sound waves by AGN jets in the intracluster medium. Astrophys. J. 886 (2), 78.CrossRefGoogle Scholar
Barnes, A. 1966 Collisionless damping of hydromagnetic waves. Phys. Fluids 9, 1483–1495.CrossRefGoogle Scholar
Bernstein, I. B. & Kulsrud, R. M. 1960 Ion wave instabilities. Phys. Fluids 3 (6), 937–945.CrossRefGoogle Scholar
Braginskii, S. I. 1965 Transport processes in a plasma. Rev. Plasma Phys. 1, 205.Google Scholar
Chandrasekhar, S., Kaufman, A. N. & Watson, K. M. 1958 The stability of the pinch. Proc. R. Soc. Lond. A 245, 435–455.Google Scholar
Chen, C. H. K., Matteini, L., Schekochihin, A. A., Stevens, M. L., Salem, C. S., Maruca, B. A., Kunz, M. W. & Bale, S. D. 2016 Multi-species measurements of the firehose and mirror instability thresholds in the solar wind. Astrophys. J. Lett. 825, L26.CrossRefGoogle Scholar
Chew, G. F., Goldberger, M. L. & Low, F. E. 1956 The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Lond. A 236, 112–118.Google Scholar
Davidson, R. C. & Völk, H. J. 1968 Macroscopic quasilinear theory of the garden-hose instability. Phys. Fluids 11, 2259–2264.CrossRefGoogle Scholar
Fabian, A. C., Reynolds, C. S., Taylor, G. B. & Dunn, R. J. H. 2005 On viscosity, conduction and sound waves in the intracluster medium. Mon. Not. R. Astron. Soc. 363 (3), 891–896.CrossRefGoogle Scholar
Fabian, A. C., Sanders, J. S., Allen, S. W., Crawford, C. S., Iwasawa, K., Johnstone, R. M., Schmidt, R. W. & Taylor, G. B. 2003 A deep Chandra observation of the Perseus cluster: shocks and ripples. Mon. Not. R. Astron. Soc. 344 (3), L43–L47.CrossRefGoogle Scholar
Fabian, A. C., Walker, S. A., Russell, H. R., Pinto, C., Sanders, J. S. & Reynolds, C. S. 2017 Do sound waves transport the AGN energy in the Perseus cluster? Mon. Not. R. Astron. Soc. 464 (1), L1–L5.CrossRefGoogle Scholar
Fried, B. D. & Gould, R. W. 1961 Longitudinal ion oscillations in a hot plasma. Phys. Fluids 4 (1), 139–147.CrossRefGoogle Scholar
Hasegawa, A. 1969 Drift mirror instability of the magnetosphere. Phys. Fluids 12, 2642–2650.CrossRefGoogle Scholar
Hellinger, P. 2007 Comment on the linear mirror instability near the threshold. Phys. Plasmas 14, 082105.CrossRefGoogle Scholar
Hellinger, P. 2017 Proton firehose instabilities in the expanding solar wind. J. Plasma Phys. 83 (1), 705830105.CrossRefGoogle Scholar
Hellinger, P. & Matsumoto, H. 2000 New kinetic instability: oblique Alfvén fire hose. J. Geophys. Res. 105, 10519.CrossRefGoogle Scholar
Hellinger, P., Trávníček, P., Kasper, J. C. & Lazarus, A. J. 2006 Solar wind proton temperature anisotropy: linear theory and WIND/SWE observations. Geophys. Res. Lett. 33, L09101.CrossRefGoogle Scholar
Hellinger, P. & Trávníček, P. M. 2015 Proton temperature-anisotropy-driven instabilities in weakly collisional plasmas: hybrid simulations. J. Plasma Phys. 81 (1), 305810103.CrossRefGoogle Scholar
Kanekar, A., Schekochihin, A. A., Dorland, W. & Loureiro, N. F. 2015 Fluctuation-dissipation relations for a plasma-kinetic Langevin equation. J. Plasma Phys. 81, 305810104.CrossRefGoogle Scholar
Kasper, J. C., Lazarus, A. J. & Gary, S. P. 2002 Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys. Res. Lett. 29, 1839.CrossRefGoogle Scholar
Kempski, P., Quataert, E. & Squire, J. 2020 Sound-wave instabilities in dilute plasmas with cosmic rays: implications for cosmic ray confinement and the Perseus X-ray ripples. Mon. Not. R. Astron. Soc. 493 (4), 5323–5335.CrossRefGoogle Scholar
Kennel, C. F. & Sagdeev, R. Z. 1967 Collisionless shock waves in high ${\beta }$ plasmas: 1. J. Geophys. Res. 72 (13), 3303–3326.CrossRefGoogle Scholar
Komarov, S. V., Churazov, E. M., Kunz, M. W. & Schekochihin, A. A. 2016 Thermal conduction in a mirror-unstable plasma. Mon. Not. R. Astron. Soc. 460, 467–477.CrossRefGoogle Scholar
Kulsrud, R. & Pearce, W. P. 1969 The effect of wave-particle interactions on the propagation of cosmic rays. Astrophys. J. 156, 445.CrossRefGoogle Scholar
Kunz, M. W. 2011 Dynamical stability of a thermally stratified intracluster medium with anisotropic momentum and heat transport. Mon. Not. R. Astron. Soc. 417, 602–616.CrossRefGoogle Scholar
Kunz, M. W., Schekochihin, A. A., Chen, C. H. K., Abel, I. G. & Cowley, S. C. 2015 Inertial-range kinetic turbulence in pressure-anisotropic astrophysical plasmas. J. Plasma Phys. 81, 325810501.CrossRefGoogle Scholar
Kunz, M. W., Schekochihin, A. A. & Stone, J. M. 2014 a Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 112 (20), 205003.CrossRefGoogle Scholar
Kunz, M. W., Stone, J. M. & Bai, X.-N. 2014 b Pegasus: a new hybrid-kinetic particle-in-cell code for astrophysical plasma dynamics. J. Comput. Phys. 259, 154–174.CrossRefGoogle Scholar
Lithwick, Y. & Goldreich, P. 2001 Compressible magnetohydrodynamic turbulence in interstellar plasmas. Astrophys. J. 562, 279–296.CrossRefGoogle Scholar
Melville, S., Schekochihin, A. A. & Kunz, M. W. 2016 Pressure-anisotropy-driven microturbulence and magnetic-field evolution in shearing, collisionless plasma. Mon. Not. R. Astron. Soc. 459, 2701–2720.CrossRefGoogle Scholar
Meyrand, R., Kanekar, A., Dorland, W. & Schekochihin, A. A. 2019 Fluidization of collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116 (4), 1185–1194.CrossRefGoogle ScholarPubMed
Parker, E. N. 1958 Dynamical instability in an anisotropic ionized gas of low density. Phys. Rev. 109, 1874–1876.CrossRefGoogle Scholar
Quataert, E. 2008 Buoyancy instabilities in weakly magnetized low-collisionality plasmas. Astrophys. J. 673, 758–762.CrossRefGoogle Scholar
Quataert, E., Dorland, W. & Hammett, G. W. 2002 The magnetorotational instability in a collisionless plasma. Astrophys. J. 577, 524–533.CrossRefGoogle Scholar
Rincon, F., Schekochihin, A. A. & Cowley, S. C. 2015 Non-linear mirror instability. Mon. Not. R. Astron. Soc. 447, L45–L49.CrossRefGoogle Scholar
Riquelme, M., Quataert, E. & Verscharen, D. 2018 PIC simulations of velocity-space instabilities in a decreasing magnetic field: viscosity and thermal conduction. Astrophys. J. 854 (2), 132.CrossRefGoogle Scholar
Riquelme, M. A., Quataert, E. & Verscharen, D. 2015 Particle-in-cell simulations of continuously driven mirror and ion cyclotron instabilities in high beta astrophysical and heliospheric plasmas. Astrophys. J. 800, 27.CrossRefGoogle Scholar
Rosenbluth, M. N. 1956 Stability of the pinch. LANL Rep. LA-2030.Google Scholar
Rosin, M. S., Schekochihin, A. A., Rincon, F. & Cowley, S. C. 2011 A non-linear theory of the parallel firehose and gyrothermal instabilities in a weakly collisional plasma. Mon. Not. R. Astron. Soc. 413, 7.CrossRefGoogle Scholar
Ruszkowski, M., Brüggen, M. & Begelman, M. C. 2004 Cluster heating by viscous dissipation of sound waves. Astrophys. J. 611 (1), 158–163.CrossRefGoogle Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310–377.CrossRefGoogle Scholar
Schekochihin, A. A., Cowley, S. C., Kulsrud, R. M., Rosin, M. S. & Heinemann, T. 2008 Nonlinear growth of firehose and mirror fluctuations in astrophysical plasmas. Phys. Rev. Lett. 100 (8), 081301.CrossRefGoogle ScholarPubMed
Schekochihin, A. A., Parker, J. T., Highcock, E. G., Dellar, P. J., Dorland, W. & Hammett, G. W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82 (2), 905820212.CrossRefGoogle Scholar
Schlickeiser, R. 1989 Cosmic-ray transport and acceleration. I. Derivation of the kinetic equation and application to cosmic rays in static cold media. Astrophys. J. 336, 243.CrossRefGoogle Scholar
Sironi, L. & Narayan, R. 2015 Electron heating by the ion cyclotron instability in collisionless accretion flows. I. Compression-driven instabilities and the electron heating mechanism. Astrophys. J. 800, 88.CrossRefGoogle Scholar
Snyder, P. B., Hammett, G. W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4, 3974–3985.CrossRefGoogle Scholar
Southwood, D. J. & Kivelson, M. G. 1993 Mirror instability. I – Physical mechanism of linear instability. J. Geophys. Res. 98, 9181–9187.CrossRefGoogle Scholar
Squire, J., Kunz, M. W., Quataert, E. & Schekochihin, A. A. 2017 a Kinetic simulations of the interruption of large-amplitude shear-Alfvén waves in a high-$\beta$ Plasma. Phys. Rev. Lett. 119 (15), 155101.CrossRefGoogle Scholar
Squire, J., Quataert, E. & Schekochihin, A. A. 2016 A stringent limit on the amplitude of Alfvénic perturbations in high-beta low-collisionality plasmas. Astrophys. J. 830, L25.CrossRefGoogle Scholar
Squire, J., Schekochihin, A. A. & Quataert, E. 2017 b Amplitude limits and nonlinear damping of shear-Alfvén waves in high-beta low-collisionality plasmas. New J. Phys. 19 (5), 055005.CrossRefGoogle Scholar
Vedenov, A. A. & Sagdeev, R. Z. 1958 In Plasma Physics and Problems of Controlled Thermonuclear Reactions (ed. Leontovich, M. A.), p. 278. Izd. Akad. Nauk SSSR.Google Scholar
Verscharen, D., Chandran, B. D. G., Klein, K. G. & Quataert, E. 2016 Collisionless isotropization of the solar-wind protons by compressive fluctuations and plasma instabilities. Astrophys. J. 831, 128.CrossRefGoogle Scholar
Verscharen, D., Chen, C. H. K. & Wicks, R. T. 2017 On kinetic slow modes, fluid slow modes, and pressure-balanced structures in the solar wind. Astrophys. J. 840, 106.CrossRefGoogle Scholar
Xu, R. & Kunz, M. W. 2016 Linear Vlasov theory of a magnetised, thermally stratified atmosphere. J. Plasma Phys. 82 (5), 905820507.CrossRefGoogle Scholar
Yoon, P. H., Wu, C. S. & de Assis, A. S. 1993 Effect of finite ion gyroradius on the fire-hose instability in a high beta plasma. Phys. Fluids B 5, 1971.CrossRefGoogle Scholar
Zhuravleva, I., Churazov, E., Schekochihin, A. A., Allen, S. W., Vikhlinin, A. & Werner, N. 2019 Suppressed effective viscosity in the bulk intergalactic plasma. Nat. Astron. 3, 832–837.CrossRefGoogle Scholar
Zweibel, E. G., Mirnov, V. V., Ruszkowski, M., Reynolds, C. S., Yang, H. Y. K. & Fabian, A. C. 2018 Acoustic disturbances in galaxy clusters. Astrophys. J. 858 (1), 5.CrossRefGoogle Scholar