Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T00:59:29.412Z Has data issue: false hasContentIssue false
  • English
  • Français

A relativistic particle pusher for ultra-strong electromagnetic fields

Part of: The Many Facets of the Vlasov Equation Focus on Plasma Astrophysics

Published online by Cambridge University Press:  26 August 2020

J. Pétri Open the ORCID record for J. Pétri [Opens in a new window]
J. Pétri*
Affiliation:
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, F-67000Strasbourg, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kinetic plasma simulations are nowadays commonly used to study a wealth of nonlinear behaviours and properties in laboratory and space plasmas. In particular, in high-energy physics and astrophysics, the plasma usually evolves in ultra-strong electromagnetic fields produced by intense laser beams for the former or by rotating compact objects such as neutron stars and black holes for the latter. In these ultra-strong electromagnetic fields, the gyro-period is several orders of magnitude smaller than the time scale on which we desire to investigate the plasma evolution. Some approximations are required such as, for instance, artificially decreasing the electromagnetic field strength, which is certainly not satisfactory. The main flaw of this downscaling is that it cannot reproduce particle acceleration to ultra-relativistic speeds with a Lorentz factor above 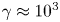$\gamma \approx 10^3$–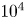$10^4$. In this paper, we design a new algorithm able to catch particle motion and acceleration to a Lorentz factor of up to 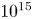$10^{15}$ or even higher by using Lorentz boosts to special frames where the electric and magnetic field are parallel. Assuming that these fields are locally uniform in space and constant in time, we solve analytically the equation of motion in a tiny region smaller than the length scale of the spatial and temporal gradient of the field. This analytical integration of the orbit severely reduces the constraint on the time step, allowing us to use large time steps, avoiding resolving the ultra-high gyro-frequency. We performed simulations in ultra-strong spatially and time-dependent electromagnetic fields, showing that our particle pusher is able to follow accurately the exact analytical solution for very long times. This property is crucial to properly capture for instance lepton electrodynamics in electromagnetic waves produced by fast rotating neutron stars. We conclude with a simple implementation of our new pusher into a one-dimensional relativistic electromagnetic particle-in-cell code, testing it against plasma oscillations, two-stream instabilities and strongly magnetized relativistic shocks.

Keywords

astrophysical plasmasplasma dynamicsplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 4 , August 2020 , 825860402
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ansoldi, S., Antonelli, L. A., Antoranz, P., Babic, A., Bangale, P., de Almeida, U. B., Barrio, J. A., González, J. B., Bednarek, W., Bernardini, E., et al. 2016 Teraelectronvolt pulsed emission from the Crab Pulsar detected by MAGIC. Astron. Astrophys. 585, A133.10.1051/0004-6361/201526853CrossRefGoogle Scholar
Arefiev, A. V., Cochran, G. E., Schumacher, D. W., Robinson, A. P. L. & Chen, G. 2015 Temporal resolution criterion for correctly simulating relativistic electron motion in a high-intensity laser field. Phys. Plasmas 22 (1), 013103.10.1063/1.4905523CrossRefGoogle Scholar
Baumjohann, W. & Treumann, R. 1996 Basic Space Plasma Physics, new edn. 340 pp. Imperial College Press.10.1142/p015CrossRefGoogle Scholar
Belyaev, M. A. 2015 Dissipation, energy transfer, and spin-down luminosity in 2.5D PIC simulations of the pulsar magnetosphere. Mon. Not. R. Astron. Soc. 449 (3), 2759–2767.CrossRefGoogle Scholar
Biltzinger, P. & Thielheim, K. O. 2000 Selfconsistent numerical calculation of relativistic neutron star magnetospheres. arXiv:astro-ph/0011306.Google Scholar
Birdsall, C. K. & Langdon, A. B. 2005 Plasma physics via computer simulation. IOP.Google Scholar
Boris, J. P. 1970 Relativistic plasma simulation-optimization of a hybrid code. Proceeding of Fourth Conference on Numerical Simulations of Plasmas. Naval Research Laboratory.Google Scholar
Bowers, K. J., Albright, B. J., Yin, L., Bergen, B. & Kwan, T. J. T. 2008 Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15 (5), 055703.10.1063/1.2840133CrossRefGoogle Scholar
Cerutti, B., Philippov, A., Parfrey, K. & Spitkovsky, A. 2015 Particle acceleration in axisymmetric pulsar current sheets. Mon. Not. R. Astron. Soc. 448, 606–619.10.1093/mnras/stv042CrossRefGoogle Scholar
Cerutti, B., Philippov, A. A. & Spitkovsky, A. 2016 Modelling high-energy pulsar light curves from first principles. Mon. Not. R. Astron. Soc. 457, 2401–2414.10.1093/mnras/stw124CrossRefGoogle Scholar
Crouseilles, N., Lemou, M., Méhats, F. & Zhao, X. 2017 Uniformly accurate Particle-in-Cell method for the long time solution of the two-dimensional Vlasov–Poisson equation with uniform strong magnetic field. J. Comput. Phys. 346, 172–190.10.1016/j.jcp.2017.06.011CrossRefGoogle Scholar
Djannati-Ataï, A. & for the H.E.S.S. Collaboration 2017 H.E.S.S. stereoscopic observations of the Vela Pulsar above 100 GeV.Google Scholar
Filbet, F. & Rodrigues, L. M. 2015 Asymptotically stable particle-in-cell methods for the Vlasov–Poisson system with a strong external magnetic field. arXiv:1511.07400.Google Scholar
Finkbeiner, B., Herold, H., Ertl, T. & Ruder, H. 1989 Effects of radiation damping on particle motion in pulsar vacuum fields. Astron. Astrophys. 225, 479–487.Google Scholar
Geiser, J. & Frederik, R. 2016 Integrators for particle in cell methods: comparison and applications. AIP Conf. Proc. 1738 (1), 480009.10.1063/1.4952245CrossRefGoogle Scholar
Giovanelli, R. 1987 Analytic treatment of the relativistic motion of charged particles in electric and magnetic field. Il Nuovo Cimento D 9 (11), 1443–1460.CrossRefGoogle Scholar
Gordon, D. F., Hafizi, B. & Palastro, J. 2017 Pushing particles in extreme fields. AIP Conf. Proc. 1812 (1),050002.CrossRefGoogle Scholar
Gourgoulhon, E. 2010 Relativité restreinte: Des particules à l'astrophysique. EDP Sciences.Google Scholar
Gruzinov, A. 2013 Aristotelian electrodynamics solves the pulsar: lower efficiency of strong pulsars. arXiv:1303.4094.Google Scholar
Hadad, Y., Labun, L., Rafelski, J., Elkina, N., Klier, C. & Ruhl, H. 2010 Effects of radiation reaction in relativistic laser acceleration. Phys. Rev. D 82 (9), 096012.10.1103/PhysRevD.82.096012CrossRefGoogle Scholar
Heintzmann, H. & Schrüfer, E. 1973 Exact solutions of the Lorentz-Dirac equations of motion for charged particles in constant electromagnetic fields. Phys. Lett. A 43 (3), 287–288.CrossRefGoogle Scholar
Higuera, A. V. & Cary, J. R. 2017 Structure-preserving second-order integration of relativistic charged particle trajectories in electromagnetic fields. Phys. Plasmas 24 (5), 052104.CrossRefGoogle Scholar
Jackson, J. D. 2001 Electrodynamiqueclassique: Cours et exercices d'electromagnétisme. Dunod.Google Scholar
Kalapotharakos, C., Brambilla, G., Timokhin, A., Harding, A. K. & Kazanas, D. 2018 Three-dimensional kinetic pulsar magnetosphere models: connecting to gamma-ray observations. Astrophys. J. 857 (1), 44.10.3847/1538-4357/aab550CrossRefGoogle Scholar
Kirk, J. G., Lyubarsky, Y. & Petri, J. 2009 The theory of pulsar winds and nebulae, vol. 357, pp. 421–450. Springer.Google Scholar
Lapenta, G. & Markidis, S. 2011 Particle acceleration and energy conservation in particle in cell simulations. Phys. Plasmas 18 (7), 072101.CrossRefGoogle Scholar
Laue, H. & Thielheim, K. O. 1986 Acceleration of protons and electrons in the electromagnetic field of a rotating orthogonal magnetic dipole. Astrophys. J. Suppl. Ser. 61, 465–478.CrossRefGoogle Scholar
Lyubarsky, Y. 2005 The termination shock in a striped pulsar wind. Adv. Space Res. 35 (6), 1112–1115.10.1016/j.asr.2005.01.025CrossRefGoogle Scholar
Mereghetti, S., Pons, J. A. & Melatos, A. 2015 Magnetars: properties, origin and evolution. Space Sci. Rev. 191 (1–4), 315–338.CrossRefGoogle Scholar
Mestel, L. 1999 Stellar Magnetism, International Series of Monographs on Physics, vol. 99. Clarendon.Google Scholar
Michel, F. C. & Li, H. 1999 Electrodynamics of neutron stars. Phys. Rep. 318 (6), 227–297.10.1016/S0370-1573(99)00002-2CrossRefGoogle Scholar
Patacchini, L. & Hutchinson, I. H. 2009 Explicit time-reversible orbit integration in Particle In Cell codes with static homogeneous magnetic field. J. Comput. Phys. 228 (7), 2604–2615.10.1016/j.jcp.2008.12.021CrossRefGoogle Scholar
Philippov, A. A. & Spitkovsky, A. 2014 Ab Initio pulsar magnetosphere: three-dimensional particle-in-cell simulations of axisymmetric pulsars. Astrophys. J. Lett. 785 (2), L33.10.1088/2041-8205/785/2/L33CrossRefGoogle Scholar
Piazza, A. D. 2008 Exact solution of the Landau–Lifshitz equation in a plane wave. Lett. Math. Phys. 83 (3), 305–313.10.1007/s11005-008-0228-9CrossRefGoogle Scholar
Press, W. H. 2007 Numerical Recipes the Art of Scientific Computing. Cambridge University Press.Google Scholar
Pétri, J. 2016 Theory of pulsar magnetosphere and wind. J. Plasma Phys. 82 (5), 635820502.CrossRefGoogle Scholar
Pétri, J. 2017 A fully implicit scheme for numerical integration of the relativistic particle equation of motion. J. Plasma Phys. 83 (02).CrossRefGoogle Scholar
Pétri, J. 2019 Pulsar gamma-ray emission in the radiation reaction regime. Mon. Not. R. Astron. Soc. 484 (4), 5669–5691.10.1093/mnras/stz360CrossRefGoogle Scholar
Pétri, J. & Lyubarsky, Y. 2007 Magnetic reconnection at the termination shock in a striped pulsar wind. Astron. Astrophys. 473, 683–700.CrossRefGoogle Scholar
Qin, H., Zhang, S., Xiao, J., Liu, J., Sun, Y. & Tang, W. M. 2013 Why is Boris algorithm so good? Phys. Plasmas 20 (8), 084503.10.1063/1.4818428CrossRefGoogle Scholar
Ripperda, B., Bacchini, F., Teunissen, J., Xia, C., Porth, O., Sironi, L., Lapenta, G. & Keppens, R. 2018 A comprehensive comparison of relativistic particle integrators. Astrophys. J. Suppl. Ser. 235 (1), 21.10.3847/1538-4365/aab114CrossRefGoogle Scholar
Sengupta, P. 2007 Classical Electrodynamics. New Age International Pvt Ltd.Google Scholar
Shen, C. S. 1978 Radiation and acceleration of a relativistic charged particle in an electromagnetic field. Phys. Rev. D 17 (2), 434–445.10.1103/PhysRevD.17.434CrossRefGoogle Scholar
Spreiter, Q. & Walter, M. 1999 Classical molecular dynamics simulation with the velocity Verlet algorithm at strong external magnetic fields. J. Comput. Phys. 152 (1), 102–119.CrossRefGoogle Scholar
Tomczak, I. & Pétri, J. 2020 Particle acceleration in neutron star ultra-strong electromagnetic fields. J. Plasma Phys. (submitted) arXiv:2007.04797.10.1017/S0022377820000835CrossRefGoogle Scholar
Umeda, T. 2018 A three-step Boris integrator for Lorentz force equation of charged particles. Comput. Phys. Commun. 228, 1–4.10.1016/j.cpc.2018.03.019CrossRefGoogle Scholar
Uzan, J.-P. & Deruelle, N. 2014 Théories de la Relativité. Belin.Google Scholar
Vandervoort, P. O. 1960 The relativistic motion of a charged particle in an inhomogeneous electromagnetic field. Ann. Phys. 10 (3), 401–453.CrossRefGoogle Scholar
Vay, J.-L. 2008 Simulation of beams or plasmas crossing at relativistic velocity. Phys. Plasmas 15 (5), 056701.10.1063/1.2837054CrossRefGoogle Scholar
Verboncoeur, J. P. 2005 Particle simulation of plasmas: review and advances. Plasma Phys. Control. Fusion 47 (5A), A231.10.1088/0741-3335/47/5A/017CrossRefGoogle Scholar
Verlet, L. 1967 Computer experiments on classical fluids. I. Thermodynamical properties of Lennard–Jones molecules. Phys. Rev. 159 (1), 98–103.10.1103/PhysRev.159.98CrossRefGoogle Scholar
Vranic, M., Martins, J. L., Fonseca, R. A. & Silva, L. O. 2016 Classical radiation reaction in particle-in-cell simulations. Comput. Phys. Commun. 204, 141–151.CrossRefGoogle Scholar
Zenitani, S. & Umeda, T. 2018 On the Boris solver in particle-in-cell simulation. arXiv:1809.04378.10.1063/1.5051077CrossRefGoogle Scholar
Zhang, R., Liu, J., Qin, H., Wang, Y., He, Y. & Sun, Y. 2015 Volume-preserving algorithm for secular relativistic dynamics of charged particles. Phys. Plasmas 22 (4), 044501.CrossRefGoogle Scholar