Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T00:36:04.449Z Has data issue: false hasContentIssue false
  • English
  • Français

Plasma microinstabilities driven by loss-cone distributions

Published online by Cambridge University Press:  13 March 2009

Danny Summers  and
Richard M. Thorne
Danny Summers
Affiliation:
Department of mathematics and Statistics, Memorial University of Newfoundland, St John's Newfoundland, CanadaA1C5 S7
Richard M. Thorne
Affiliation:
Department of atmospheric Sciences, University of California at Los Angeles, California 90024–1565, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Electromagnetic and electrostatic instabilities driven by loss-cone particle distributions have been invoked to explain a variety of plasma phenomena observed in space and in the laboratory. In this paper we analyse how the loss- cone feature (as determined by the loss-cone index or indices) influences the growth of such instabilities in a fully ionized, homogeneous, hot plasma in a uniform magnetic field. Specifically, we consider three loss-cone distributions: a generalized Lorentzian (kappa) loss-cone distribution, the Dory—Guest—Harris distribution and the Ashour-Abdalla-Kennel distribution (involving a subtracted Maxwellian). Our findings are common to all three distributions. We find that, for parallel propagation, electromagnetic instabilities are only affected by the loss-cone indices in terms of their occurrence in the temperature anisotropy. However, for oblique propagation, even including propagation at small angles to the ambient magnetic field, the loss-cone indices do independently affect the growth of instabilities for electromagnetic waves, in contrast to certain claims in the literature. 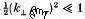For electrostatic waves such that 1, where kx is the component of the wave vector perpendicular to the ambient magnetic field and pLa is the Larmor radius for particle species <r, we find that the loss-cone indices only enter the dispersion equation via the temperature anisotropy, and so in this case the loss-cone feature and perpendicular effective thermal speed do not independently affect wave growth.

Type
Research Article
Information
Journal of Plasma Physics , Volume 53 , Issue 3 , June 1995 , pp. 293 - 315
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, M. 1986 Ann. Geophys. 4A, 241.Google Scholar
Ashour-Abdalla, M. & Kennel, C. F. 1978 J. Geophys. Res. 83, 1531.CrossRefGoogle Scholar
Baldwin, D. E. 1977 Rev. Mod. Phys. 49, 317.Google Scholar
Brinca, A. L. 1972 J. Geophys. Res. 77, 3495.Google Scholar
Coroniti, F. V., Fredricks, R. W. & Whiter, R. 1972 J. Geophys. Res. 77, 6243.Google Scholar
Denton, R. E., Hudson, M. K. & Roth, I. 1992 J. Geophys. Res. 97, 12093.Google Scholar
Dory, R. A., Guest, G. E. & Harris, E. G. 1965 Phys. Rev. Lett. 14, 131.CrossRefGoogle Scholar
Dysthe, K. B. 1971 J. Geophys. Res. 76, 6915.Google Scholar
Fried, B. D. & Conte, S. D. 1961 The Plasma Dispersion Function. Academic.Google Scholar
Fung, S. F. & Viñas, A. F. 1994 J. Geophys. Res. 99, 8671.Google Scholar
Gomberoff, L. & Cuperman, S. 1981 J. Plasma Phys. 25, 99.Google Scholar
Harris, E. G. 1961 J. Nucl. Energy C 2, 138.Google Scholar
Hewitt, R. G. & Melrose, D. B. 1985 Solar Phys. 96, 157.Google Scholar
Hewitt, R. G., Melrose, D. B. & Rönnmark, K. G. 1982 Aust. J. Phys. 35, 447.Google Scholar
Horne, R. B. 1989 J. Geophys. Res. 94, 8895.Google Scholar
Huang, L., Hawkins, J. G. & Lee, L. C. 1990 J. Geophys. Res. 95, 3893.Google Scholar
Ichimaru, S., 1973 Basic Principles of Plasma Physics. Benjamin.Google Scholar
Kennel, C. 1966 Phys. Fluids 9, 2190.Google Scholar
Krall, N. A. & Trivelpice, A. W. 1973 Principles of Plasma Physics. McGraw-Hill.CrossRefGoogle Scholar
Landau, R. W. & Cuperman, S. 1971 J. Plasma Phys. 6, 495.Google Scholar
Lee, J. C. & Crawford, F. W. 1970 J. Geophys. Res. 75, 85.CrossRefGoogle Scholar
Melrose, B. B. 1986 Instabilities in Space and Laboratory Plasmas. Cambridge University Press.Google Scholar
Meng, Z., Thorne, R. M. & Summers, B. 1992 J. Plasma Phys. 47, 445.Google Scholar
Olbert, S. 1968 Physics of the Magnetosphere (ed. Carovillano, R. L., McClay, J. F. & Radoski, H. R.), p. 641. Springer.Google Scholar
Post, R. F. & Rosenbluth, M. N. 1966 Phys. Fluids 9, 730.Google Scholar
Rönnmark, K. 1983 Plasma Phys. 25, 699.Google Scholar
Summers, D. & Thorne, R. M. 1987 Phys. Fluids 30, 3761.Google Scholar
Summers, D. & Thorne, R. M. 1991 Phys. Fluids B3, 1835.Google Scholar
Summers, D. & Thorne, R. M. 1992 J. Geophys. Res. 97, 16827.Google Scholar
Summers, D.Xue, S. & Thorne, R. M. 1994 Phys. Plasmas 1, 2012.Google Scholar
Swanson, B. G. 1989 Plasma Waves. Academic.Google Scholar
Swift, D. W. 1968 J. Geophys. Res. 73, 7447.Google Scholar
Thorne, R. M. & Summers, D. 1986 Phys. Fluids 29, 4091.Google Scholar
Thorne, R. M. & Summers, D. 1988a Ann. Geophys. 6, 275.Google Scholar
Thorne, R. M. & Summers, D. 1988b J. Plasma Phys. 39, 485.Google Scholar
Thorne, R. M. & Summers, D. 1991 Phys. Fluids B 3, 2117.Google Scholar
Vasyliunas, V. M. 1968 J. Geophys. Res. 73, 2839.CrossRefGoogle Scholar
Willes, A. J. & Robinson, P. A. 1994 J. Plasma Phys. 51, 75.Google Scholar
Wong, H. K., Wu, C. S., Ke, F. J., Schneider, R. S. & Ziebell, L. F. 1982 J. Plasma Phys. 28, 503.Google Scholar
Wu, C. S. & Lee, L. C. 1979 Astrophys. J. 230, 621.Google Scholar
Wu, C. S. & Qiu, X. M. 1983 J. Geophys. Res. 88, 10072.Google Scholar
Xue, S., Throne, R. M. & Summers, D. 1993a Physics of Space Plasmas (1992): SPI Conference Proceedings and Reprint Series, No. 12 (ed. Chang, T. & Jasperse, J. R.), p. 619. Scientific.Google Scholar
Xue, S., Thorne, R. M. & Summers, D. 1993b J. Geophys. Res. 98, 17475.Google Scholar
Yoon, P. H. & Krauss-varban, D. 1990 Phys. Fluids B 2, 1918.Google Scholar