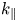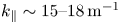2. ICRF core wave absorption on SPARC

For the ICRF application on SPARC, the antennae launch the fast magnetosonic wave (fast wave), predominantly having an electric field ${E_{fw}}\, \bot \,B$. After entering the plasma edge, the fast wave can interact with ions species at fundamental IC or second harmonic IC resonances, heat electrons via Landau damping and has some collisional damping near the plasma edge. The wave power would ultimately be dissipated in the plasma after multiple passes and/or reflections. However, not all absorption mechanisms are equal for the effectiveness of heating. It is better to have power deposition centred at the magnetic axis and absorbed on the targeted species (minority ions, main fusion ions or electrons). The single-pass-absorption (SPA) calculation is a simple and useful tool to assess the heating effectiveness. Based on the Alcator C-Mod experience, if a heating scheme has high SPA and the absorption regime is localized on-axis, the scheme generally performs well.

The SPA is calculated using the method and formula of Porkolab (Reference Porkolab, Stix and Fisch1994). Given plasma parameters along the mid-plane and wave ${k_\parallel }$, we can solve the wave roots k_x (both fast wave and slow wave) from the hot plasma dispersion equation, where x is in the wave propagation direction. In hot plasma dispersion, k_x is a complex value because of power dissipation. When the wave propagates through the region with non-zero Im(k_x), the remaining power would be exponentially damped by a factor of $\textrm{exp}( - 2\int {{k_x}\,\textrm{d}x} )$. The SPA then is simply defined as $\textrm{SPA} = 1 - \textrm{exp}( - 2\int {{k_x}\,\textrm{d}x} )$. As a result, the thicker the absorption region or the larger Im(k_x) is, the more wave power is absorbed by the plasma.

For the D(³He) minority heating scenario, the wave frequency is at the ³He fundamental frequency and the region with large Im(k_x) is localized between the ³He cyclotron resonance and the D-³He hybrid layer. The IC resonance layer provides the mechanism for wave absorption and the hybrid layer produces the correct left-handed wave polarization for absorption. Successful minority heating requires the two layers to be close in space. The magnitude of Im(k_x) in the absorption region is a complicated function of the relative mass-to-charge ratio A/Z of the majority versus the minority species and the Doppler broadening of the cyclotron resonance. The choice of the species influences the SPA through the wave polarization term near the ion–ion hybrid layer. For example, D(H) has more favourable relative A/Z ratio, higher fraction of left-handed polarization and, thus, significantly higher SPA than D(³He). This was shown in the C-Mod experience, where D(H) heating was much more effective. Importantly, T(³He) has the same relative A/Z as D(H) so improved polarization is expected in D–T(³He) plasmas. The Doppler broadening effect is larger at higher tail temperature, larger machine size (because the B field changes more slowly along the major radius) and larger ${k_\parallel }$. The distance between the hybrid layer and the cyclotron layer is proportional to the minority concentration defined as $\textrm{X}{(^3}\textrm{He}) = {n_{He3}}/{n_e}$, therefore the minority concentration term affects the overlapping of the Doppler broadened IC resonance and the ion–ion hybrid layer and also the wave polarization. Although at very low concentration, even if the ion–ion hybrid layer and the IC resonance are very close, the absorption would drop because of too few resonant particles. The minority tail temperature affects the Doppler broadening, but the tail temperature itself is dependent on wave power density, electron density and minority concentration. For the ICRF design on SPARC, we seek to identify the effective heating regime in a multi-dimensional parameter space, and the regime needs to be fairly broad in theory and experimentally simple to reach and maintain.

To assess the situation on SPARC, we mainly focus on minority concentration X(³He), ${k_\parallel }$, and tail temperature ${T_{^3He}}$. The numerical solutions of the hot plasma dispersion equation for k_x versus major radius for D(³He) minority heating on SPARC at two different tail temperatures (10 and 80 keV) are shown in figure 1(a). The background plasma is in L-mode with T_{e 0} ~ 6 keV and n_{e 0} = 4.0 × 10²⁰ m⁻³, X(³He) = 6 % and ${k_\parallel }$ at antenna = 15 m⁻¹. The plasma parameters are obtained from the SPARC transport study (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). In the numerical calculation, the Doppler broadening effect of the cyclotron resonance layer is embedded in the respective dielectric terms of the hot plasma dispersion equation. From the k_x curves in figure 1(a), SPA can be calculated numerically to be 55 % and 87 % for tail temperature of 10 and 80 keV, respectively. The wave solution for a D–T(³He) plasma is shown in figure 1(b), with X(³He) = 6 % and X(D) = X(T) = 44 %. Im(k_x) near the ³He cyclotron layer is shown to be much larger than the case in figure 1(a). There are two factors behind the enhanced Im(k_x). First, the relative A/Z of T versus ³He in T(³He) is the same as the A/Z of D versus H in D(H), and the wave polarization is more favourable for minority heating than D(³He). Second, the second harmonic tritium IC resonance is at the same location as ³He fundamental IC and it contributes to Im(k_x) from the finite Larmor radius (FLR) effect. Unlike the fundamental IC heating, the second harmonic FLR effect is not influenced by the wave polarization, but is only sensitive to the tritium ion temperature and density. The SPA for the cases in figure 1(b) are 60 % and 97 % for tail 10 and 80 keV, respectively. As a result, similar to the success on JET and TFTR D–T campaigns, D–T(³He) plasmas are expected to have a very good wave absorption on SPARC. The ³He minority heating can start at low temperature, and then after the tritium ion temperature rises, the second harmonic T heating will contribute more.

Figure 1. Numerical solution of k_x for the hot plasma dispersion equation at different tail temperatures: (a) D(³He) case; (b) D–T(³He). The D-³He ion–ion hybrid-layer (IIH) and the ion cyclotron resonance for ³He and D ions are also labelled.

To assess operation parameter space, in figure 2 the SPA is plotted versus X(³He) and ${k_\parallel }$ for the case with 80 keV tail. Figure 2(a) is for SPARC and figure 2(b) is for a typical C-Mod plasma (8 T and 80 MHz). It is evident that there is a large parameter space for SPARC antenna to have good SPA at this tail temperature and it is expected to be much more efficient than the case of D(³He) heating on C-Mod. Although total rf power on SPARC is much larger, the power density per particle is similar to that on C-Mod. The better absorption on SPARC is mainly a result of the larger machine size.

Figure 2. SPA comparison for D(³He) heating versus X(³He) and ${k_\parallel }$ at a tail temperature of 80 keV: (a) SPARC 12T/120 MHz; (b) Alcator C-Mod 8 T/80 MHz.

In figure 3, the SPA versus tail temperature ${T_{^3He}}$, concentration of ³He X(³He) and ${k_\parallel }$ is shown for the D(³He) case, whereas the case for D–T(³He) is shown in figure 4. In figure 3(a), the contours of SPA versus ${T_{^3He}}$ and X(³He) at a fixed ${k_\parallel } = 15\,{\textrm{m}^{ - 1}}$ shows that X(³He) ~ 5 % is the best to start heating before there is a tail and, after a tail has been built-up, sensitivity versus X(³He) becomes broad. In figure 3(b), the contours of SPA versus ${T_{^3He}}$ and ${k_\parallel }$ at a fixed X(³He) = 5 % shows that ${k_\parallel } = 15$ to 20 m⁻¹ is the best range to start heating before tail generation, and after a tail has been built, the response versus ${k_\parallel }$ is also quite broad. For ${k_\parallel } \lt 10\,{\textrm{m}^{ - 1}}$, the wave interaction with the thermal ³He minority ions decreases, leading to weak absorption.

Figure 3. Parameter scan for SPA of the D(³He) case: (a) fixed ${k_\parallel } = 15\,{\textrm{m}^{ - 1}}$; (b) fixed X(³He) = 5 %.

Figure 4. Parameter scan for SPA of the D–T(³He) case: (a) fixed ${k_\parallel } = 15\,{\textrm{m}^{ - 1}}$; (b) fixed X(³He) = 5 %.

In figure 4(a,b), the result for D–T(³He) shows similar optimal range for X(³He) and ${k_\parallel }$, but, in general, the SPA is much higher than that of D(³He). In a separate scan with frequency, it is found that having the ³He IC resonance layer slightly on the lower field side of magnetic axis has better SPA than with the IC layer exactly on axis, given other parameters are identical. This seems to be related to the slightly increased Doppler width of the IC layer for this setup, and that plasma axis is between the IC layer and the hybrid layer, where the interaction of the fast wave and the resonant ions occurs the strongest.

As shown previously, SPA for SPARC is generally sufficiently high for the wave to be absorbed when there is a minority tail and/or high tritium temperature. Being a tokamak heated solely by ICRF, there is a natural question to be answered: if starting from a not-so-warm thermal plasma and starting with not-so-strong SPA, will the minority tail be generated and good heating be attainable? The concern arises from the dependence of the SPA versus the minority tail, i.e. the higher tail temperature, the better absorption. For example, if the total rf power is too low and/or the starting SPA is too small, the wave power may not be able to create a tail (which itself depends on rf power density) to push the heating process into the optimal regime. This is a unique issue for a solely ICRF heated machine whereas in other machines the background minority ions or the background tritium ions can be heated with other means and ICRF only needs to provide additional heating.

A model has been developed to analyse the situation and it shows that a path to optimal heating does exist for a broad plasma and rf parameter space in SPARC. The simple dynamic model is setup as follows: starting with total rf power and thermal minority ions, calculate the multiple-pass total absorption, and use the portion of the rf power to minority ions to calculate minority tail temperature; the minority tail temperature is then used to calculate the SPA for the next step. In the model, ${k_\parallel }$ is assumed to be constant after each reflection. An equilibrium tail temperature can be reached and it gives the total multiple-pass absorption efficiency.

For simplicity and for exploratory purpose, the minority tail temperature in this model for a given heating scenario is calculated from Stix's formula (Stix Reference Stix1975), where higher absorbed power per volume, lower minority concentration and lower plasma density are favourable to generate higher T_tail. With T_tail, SPA is then calculated from the method above by solving the hot plasma dispersion equation. Note the SPA calculation includes all absorption mechanisms, i.e. fast wave direct heating and mode conversion heating via the mode-converted short-wavelength waves, and in D–T(³He) case, power to tritium ions. For this model, only the power to the minority ions is needed in each iteration to calculate the tail temperature. The power allocation among the different heating mechanisms can be approximately inferred from TORIC simulation (Brambilla Reference Brambilla1999), where power deposition is calculated assuming 100 % power absorption by plasma. The volume for absorption is also estimated from the TORIC simulation to calculate the power density as the input to Stix's formula. The wave that is not absorbed in the first pass would be reflected from the high field edge and then passes through the absorption region for the second time. Every reflection would lose some power (leaking through the edge cutoff layer or reaching the absorption region far away from the plasma axis). The total effective heating power is calculated with three passes and in each pass the wave power is absorbed with the SPA and have a 5 % loss. The remaining power after three passes is assumed to be lost or ineffective for heating.

Unlike more sophisticated simulation codes, where the total power absorption is usually a given parameter and an accurate tail temperature thus can be calculated, this simple model would estimate how much power can be effectively absorbed and determine whether a tail temperature is reachable for a device with only ICRF heating. This model is useful in finding the main parameter dependence and their ranges for effective heating for SPARC.

Figure 5 shows the contour of the equilibrium total power absorption from the dynamic model versus rf power, X(³He) and ${k_\parallel }$ for the D(³He) case in figures 1 and 3. The equilibrium tail temperature and total absorption is calculated starting from a thermal background after a number of iterations. In figure 5(a), X(³He) ~ 5 % is shown to have highest total absorption for a large range of rf power level (i.e. even with small amount rf power, a tail can be built). For the ${k_\parallel }$ scan shown in figure 5(b), a range of $10\,{\textrm{m}^{ - 1}} \lt {k_\parallel } \lt 20\,{\textrm{m}^{ - 1}}$ would be good enough for heating. In the optimal X(³He) and ${k_\parallel }$ regime, good absorption can be attained at low total rf power, but outside this regime, especially when ${k_\parallel }$ is too small, effective heating may not be attainable.

Figure 5. Parameter scan for total absorption for the D(³He) case: (a) fixed ${k_\parallel } = 15\,{\textrm{m}^{ - 1}}$; (b) fixed X(³He) = 5 %.

For the D–T(³He) case, the situation is even better (figure 6). With the absorption from tritium ions and a more favourable polarization term, the total absorption is much stronger than in D(³He). For a broad parameter space, the total absorption can be >80 %. Note that the second harmonic T heating is a FLR effect, thus higher temperature improves absorption strength whereas ³He minority has strong absorption in the initial plasma conditions. Thus, the two main absorption mechanisms in D–T plasma have a synergistic effect and it ensures a path to high performance via ICRF heating alone. Plasma performance analysis with good heating, i.e. assuming the heating process can be achieved and rf power has been absorbed effectively, can be found in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).

Figure 6. Parameter scan for total absorption for the D–T(³He) case: (a) fixed ${k_\parallel } = 15\,{\textrm{m}^{ - 1}}$; (b) fixed X(³He) = 5 %.

Total multiple-pass absorption is a sensitive function of the single-pass loss, especially in the situations that SPA is low. For the calculation in figures 5 and 6, a value of 5% single-pass loss is assumed across the parameter space. If using a larger single-pass loss fraction, the total absorption shown in figures 5 and 6 will be lower. However, it would not affect the parameter regime for best heating. The single-pass loss depends on plasma conditions and it can have a large range. For example, in Petty et al. (Reference Petty, Pinsker, Mayberry, Porkolab, Baity, Bonoli, Chiu, de Haas, Goulding and Hoffrnan1992) single-pass loss of the order of 5 % was deduced from the DIII-D fast wave experiment, and in Lerche et al. (Reference Lerche, Van Eester, Ongena, Mayoral, Laxaback, Rimini, Argouarch, Beaumont, Blackman and Bobkov2011) single-pass loss of the order of 20 % was shown to be necessary to match the ITER-like antenna experiments on JET. For the D(H) heating on C-Mod, the calculated SPA is ~90 % with ~100 keV H tail and the effective total absorption is typically ~80–90 %, as calculated from the change of plasma stored energy. Therefore, the single-pass loss is generally <10 %. To minimize the effect of the single-pass loss to the total absorption, the SPARC antennae will be designed to mostly operate inside the regime with high SPA for effective heating.

In the pre-nuclear operation, we may also run plasmas at reduced field, for example, B_{t 0} = 8 T. With 120 MHz rf, a good choice is hydrogen minority D(H) heating in D majority plasma or ⁴He(H) in ⁴He majority plasma. H minority heating has been shown to be very effective on C-Mod at 80 MHz 5.4 T and in many other tokamaks. There is no concern here for core absorption. In addition to projected good absorption, the pre-nuclear operation can be used to test out the entire ICRF system and check out the antenna loading issues (§ 3) and impurity issues (§ 4) before entering the D–T operation. Note that H-minority heating also works for D–T(H) for the reduced field operation.

The study suggests that the ${k_\parallel }$ of the launched fast wave in the range of 10–20 m⁻¹ would have the broadest allowance for other parameters for the heating to be effective. Note that in terms of ${N_\parallel }$, the index of reflection ${N_\parallel } = c{k_\parallel }/\omega$, this range of ${k_\parallel }$ corresponds to ${N_\parallel }\sim 4\text{--}8$ for best core absorption. This is the same range of ${N_\parallel }$ as that on C-Mod at 80 MHz and ${k_\parallel }$ in the range of 7–13 m⁻¹ (depending on the operation phase).

Next, we estimate the potential power losses to alphas and ⁴He ash, which is ignored in the previous analysis. The concentrations of alpha particles and the accumulation of their thermalized component known as ash are both predicted by TRANSP (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) to be ~0.5 % of the electron density. ⁴He shares its ICRF resonance with deuterium on the high field side (shown in figure 1) where the polarization is unfavourable and absorption is correspondingly weak. As shown in figures 1(a) and 1(b), Im(k_x) near the D and ⁴He resonance is around two orders of magnitude smaller than that in the absorption region near the ³He resonance. In a good SPA regime, there is little ICRF power that reaches the high-field-side ⁴He/deuterium resonance and only trace amounts (much less than 1 %) of ICRF power are damped on the ash. In fact, deuterium at a concentration of about 47 % only accounts for 1 % of the ICRF damping from TORIC simulation. This unfavourable polarization does not apply to the energetic alphas because their large Doppler shift allows interaction throughout the entire plasma core in regions where polarization is favourable. Even so, we find the ICRF power lost on alphas is approximately 0.5 % so the total power lost on alphas and ash is less than 1 %. As the Larmor radius of the alphas is large enough that the FLR $({k_ \bot }{\rho _i} \ll 1)$ is violated for alphas particles, to address the concern about the accuracy of this damping calculation in TRANSP using TORIC, further study using AORSA/CQL3D outside of TRANSP with the same profiles have been carried out. AORSA/CQL3D simulations show that most wave power first drives ³He ions to T_tail < 80 keV and then the tail ³He ions collisionally damp primarily on D and T fusion fuel ions (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). In the process, only about 0.5 % of power is lost at the edge and to the alpha particles and ash. Given the strong SPA, unwanted power loss to alphas is minimized in the standard D–T(³He) operation in SPARC.

One other concern is the core absorption versus the poloidal location of the antennae. Owing to the limited number of ports, the antennae may have to be located not on the mid-plane but off-mid-plane and launching with an angle toward the plasma. The SPA analysis described previously is done with the mid-plane launch. When the fast wave is launched from other poloidal locations, the wave path would be different than that from the mid-plane. The distance between the hybrid layer and the IC resonance layer would become longer and it is equivalent to a larger X(³He) for the mid-plane launch. TORIC simulations have been carried out the check the difference in wave pattern at different launching angles. The power deposition profiles are slightly different than that from mid-plane launch because the wave trajectory intercepts the absorption region above (or below) the mid-plane. The shift can be compensated by running a slightly different wave frequency or B field and still make absorption near the plasma axis. In figure 7, the two-dimensional (2D) plot of the wave field patterns launched from antenna at different poloidal angles (0, −30° and +30°) are compared. As shown in figures 7(b) and 7(c), the waves that are not absorbed in the first pass through the absorption region are reflected at the R-cutoff at the edge. If the antenna is located poloidally too far away from the mid-plane, the reflected waves would propagate away from the plasma centre and then deposit power far off-axis, resulting in low heating effectiveness in cases that the SPA is less than optimal. It is difficult to assess quantitatively how the off-mid-plane antennae perform because experimental data from tokamaks are lacking. It is encouraging that as reported by Lerche et al. (Reference Lerche, Van Eester, Ongena, Mayoral, Laxaback, Rimini, Argouarch, Beaumont, Blackman and Bobkov2011), operating the ITER-like antenna on JET with only lower or upper half of the antenna showed no indications on negative effect on heating performance. To reduce the risk of having underperforming antennae, we plan only to have no more than two antennae on each toroidal location and minimize the poloidal separation of the antennae to keep them as close as to the mid-plane so that most of the ICRF power is launched on or near the mid-plane.

Figure 7. Wave pattern comparison from TORIC calculation for different antenna poloidal locations: (a) antenna on the mid-plane; (b) −30°; (c) +30°.

More detailed core ICRF physics studies, for example, accurate tail temperature modeling and power transport from fast ions to thermal ions, are to be carried out in the next stage of 30 % SPARC design (§ 6).

In summary, the fast wave will be effectively absorbed for a large range of plasma and wave parameters for both D–D plasmas and D–T plasmas and the unwanted losses to alphas and ash will be negligible. This study suggests that fast waves with the ${k_\parallel } = 10\text{--}20\,{\textrm{m}^{ - 1}}$ would have high heating effectiveness for a broad set of plasma parameters. Note ${k_\parallel }$ is determined by the antenna geometry and operation, i.e. the distances and phases among the current straps, so this result sets one of the important constraints for antenna design (more in § 5).

3. ICRF wave coupling in the edge, antenna load and power handling

The ICRF antenna is a load consisting of a resistive part and an inductive part where the reactive load is dominant. If the antenna load is equal to the transmission line impedance (e.g. 50 or 30 Ω for most efficient power transmission), the voltage in the transmission line and antenna would be the lowest for a given power. In reality, the resistive part of the antenna load R_ant is typically in the order of a few Ohms or less; therefore, some parts of ICRF system, including the transmission line and antenna, may have very high voltage-to-standing-wave-ratio (VSWR). The net power, VSWR and antenna load have a simple relation: ${P_{net}} = (1/2)(V_{max}^2/{Z_0}S) = (1/2)(V_{max}^2/Z_0^2){R_{ant}}$, where Z ₀ is the characteristic impedance of the transmission line and S is VSWR. Therefore, given the maximum voltage handling capability V_max of the antenna and transmission line, the maximum power the system can deliver is proportional to R_ant. For well-conditioned antennae in C-Mod, the typical maximum voltage was 30–40 kV and coupling 0.5–0.75 MW power per antenna strap. Beyond this empirical limit, the probability of having arcs in the system increased drastically. Undetected arcs can potentially cause severe damages while detected arcs would temporarily shut down the transmitter power for system protection. As a result, under the constraint of V_max, having adequate R_ant is key to fully and safely utilizing the transmitter power.

Antenna load (also known as antenna coupling) is largely determined by the wave–plasma interaction at the plasma edge and the pedestal region in H-mode. The power absorption mechanisms and absorption efficiency discussed in § 2 only play an insignificant role for coupling. For the fast wave, there is always a right-hand cutoff layer at the plasma edge. The fast wave has to tunnel through the cutoff (evanescent) layer and then it can propagate to the centre of plasma. In the evanescent regime, the wave has the approximate form of exponential decay $\textrm{exp}( - {k_\parallel }x)$, where x is the propagation distance. As a result, for most tokamaks, the antenna load is mainly determined by the distance between the antenna and the cutoff layer d, the ${k_\parallel }$ of the launched wave, and the density profile in the scrape-off layer up to the cutoff density. The right-hand cutoff density is determined by the magnetic field, wave frequency, electron density and antenna spectrum ${k_\parallel }$. Therefore, ${k_\parallel }$ affects both the distance d and the exponential decaying exponent. Although the H-mode pedestal is usually inside the cutoff layer, the steep density profile in the pedestal region creates a near discontinuity of Re(k_x) of the propagating fast wave, which acts like an impedance transformer for the wave propagation. This impedance transformation in turn reduces the equivalent antenna load. In general, the steeper and the higher the pedestal is, the smaller antenna load becomes (Parisot et al. Reference Parisot, Wukitch, Bonoli, Hughes, Labombard, Lin, Parker, Porkolab and Ram2004). Unfortunately, first-principle and predictive calculation of the antenna load is beyond state of the art, especially for a future device such as SPARC where no measured edge plasma density profile is yet available.

ICRF system operation on SPARC is expected to be rather similar to that on C-Mod because both are high-field and high-density tokamaks. We can learn from assessing the C-Mod antenna performance and estimate the main potential issues that may limit system performance on SPARC. Being a high-density compact tokamak, C-Mod was inherently more conducive for ICRF power coupling than other lower-density tokamaks because the cutoff layer is much closer to the antennae. There were 3 antennae on C-Mod, two 2-strap traditional antennae and one field-aligned 4-strap antenna (Bonoli et al. Reference Bonoli, Parker, Wukitch, Lin, Porkolab, Wright, Edlund, Graves, Lin and Liptac2007; Wukitch et al. Reference Wukitch, Garrett, Ochoukov, Terry, Hubbard, Labombard, Lau, Lin, Lipschultz and Miller2013). There is no clear dependence of the antenna load on global plasma parameters except the confinement mode. In L-mode and I-mode, the antenna load tends to be high and generally >5 Ω. For enhanced D_α (EDA) H-mode, the load is about half of the L-mode level, and the antennae can reliably run >4 MW total rf power from the three antennae (total eight current straps). In the most favourable condition, up to 6 MW has been achieved. In all, 0.5–0.6 MW per antenna strap is achievable in C-Mod EDA H-mode and up to 0.75 MW per strap in L-mode and I-mode. Launching high power into the ELM-free H-mode on C-Mod faces the toughest challenge and ELM-free H-mode usually ends by an H-mode to L-mode transition caused by the shut-down of rf power from arcs on the antenna, mostly due to too high V_max associated with a too small antenna load from the steepening pedestal. H-mode on SPARC is expected to have ELMs (Hughes et al. Reference Hughes, Howard, Rodriguez-Fernandez, Creely, Kuang, Snyder, Wilks, Sweeney and Greenwald2020) and the pedestal not as steep as that of ELM-free plasmas on C-Mod.

Here we apply the same parameter scaling to a typical C-Mod plasma and to the anticipated SPARC plasma and estimate the operational range of the antenna load on SPARC. According to Bilato et al. (Reference Bilato, Brambilla, Hartmann and Parisot2005), the antenna load scales with a factor: ${({n_{LCFS}}/{n_{cutoff}})^{2{k_\parallel }{\lambda _n}}}\,\textrm{exp(} {-}1.1{k_\parallel }d\textrm{)}$, where n_LCFS is the density at the last-closed flux surface, n_cutoff is the cutoff density, d is the distance between antenna and the cutoff layer, λ_n is the scale length of density profile in the scrape-off layer. In all, higher edge density, closer proximity of the antenna to the plasma, smaller ${k_\parallel }$ and flatter density profile all help. For C-Mod, for ${k_\parallel }$ in the range of 7–13 m⁻¹, the cutoff layer at n_cutoff = (3–8) × 10¹⁸ m⁻³ for D(H) at 5.4 T and n_cutoff = (5–12) × 10¹⁸ m⁻³ for D(³He) at 8 T. Note the cutoff density for D(H) operation is slightly smaller than that of D(³He) operation because of the difference in the ratio of frequency and B field. This range of cutoff density is usually in the limiter shadow. For SPARC n_cutoff = (7–15) × 10¹⁸ m⁻³ for ${k_\parallel }$ in the range of 10–20 m⁻¹ will be near the base of the H-mode pedestal. In figure 8(a), a typical edge density profile of SPARC (Hughes et al. Reference Hughes, Howard, Rodriguez-Fernandez, Creely, Kuang, Snyder, Wilks, Sweeney and Greenwald2020) is shown and the range of the cutoff densities and distance to the antenna is indicated. Here the density at the LCFS is ~5 × 10¹⁹ m⁻³. The LCFS is modelled to be ~2.5 cm away from the antenna and the density profile has an exponential decay length of ~1 cm along the radial direction in the scrape-off layer. Note that at the smaller ${k_\parallel }$, the cutoff layer is closer to the antenna and higher load is expected. A comparison of the antenna load of SPARC versus C-Mod is shown in figure 8(b). For this simplified baseline comparison, because the chosen SPARC profile is similar to the typical C-Mod case (Parisot et al. Reference Parisot, Wukitch, Bonoli, Hughes, Labombard, Lin, Parker, Porkolab and Ram2004), the same edge density profile as shown in figure 8(a) is used for the C-Mod calculation. Depending on the choice of ${k_\parallel }$, SPARC can have antenna load as much as 50–90 % of the C-Mod D(³He) for similar antenna structure. If we assume that SPARC antennae, after conditioning, can reach the same voltage handling capability, we would expect SPARC antennae on average to be able to deliver ~50–90 % power per current strap of C-Mod antennae for D(³He) operation. A value of 80 % is expected in the middle of the ${k_\parallel }$ range.

Figure 8. (a) Edge density profile and cutoff layers for SPARC; (b) antenna loading scaling factor comparison with C-Mod (D/E and J antennae).

In addition to the value of antenna load, the time variation of the load also affects the system operation. In addition to the L-mode and H-mode transitions, ELMs are one of the most common causes for transient behaviours in the antenna load. During the ELM bursts, the antenna load increases quickly (as much as an order of magnitude) because the density profile in the edge rises. In terms of ICRF system operation, the issue with ELMs is not with the value of the load per se, but with the magnitude and speed of the change of the antenna load. As seen by the transmitter, such rapid load changes are similar to the beginning stage of arcs in the transmission line or on the antenna. Therefore, it is a challenge for the ICRF system to maintain impedance matching in ELMs and to distinguish ELMs from real arcs. Fortunately, this problem can be resolved outside the tokamak by a well-designed transmission line matching system (Monakhov et al. Reference Monakhov, Graham, Blackman, Dowson, Durodie, Jacquet, Lehmann, Mayoral, Nightingale and Noble2013) or using active real-time matching (Lin et al. Reference Lin, Binus, Wukitch, Koert, Murray and Pfeiffer2015).

In conclusion, the antenna load on SPARC will be sufficiently high for antenna operation but it will not be as high as that on C-Mod. From the operational experience on C-Mod and load comparison, we expect that the antennae on SPARC can be designed to reliably deliver power up to 0.5–0.6 MW per current strap, but not much higher. Because ICRF heating will be the sole heating method, setting an unrealistically high expectation for antenna performance would result in planning too few antennae and increase the risk of not having enough heating power for the mission of the device. We expect a four-strap antenna to reliably deliver no more than 2 MW rf power and for a three-strap antenna to reliably deliver no more than 1.5 MW. The consequence of this power handling limit will be discussed in § 5 for the integrated ICRF system and device consideration.

4. Impurity issues for ICRF heating on SPARC

One undesirable feature of ICRF heating is the increased impurities associated with high-power operation. In cases when the impurities were a serious issue, ICRF heating could be stuck in a mode dubbed as ‘ICRF cooling’: the net heating effect from rf power absorption is overwhelmed by power loss from the increased radiation by the increased impurities.

Impurities are generally produced from the unwanted interaction of the ICRF waves (e.g. rf sheath along the magnetic lines created by slow waves) with the machine wall and the antenna surface. The impurity problem is entangled with both the power absorption in the core and antenna coupling at the edge. In general, heating with good core absorption is less prone to generate impurities, presumably there is less power left for interaction with the machine wall and antenna surfaces. In contrast, launching waves with the highest antenna loading but poor core absorption (e.g. with ${k_\parallel }\sim 0$ or monopole operation) would usually generate significant impurities. However, operation at high ICRF power, even with good absorption, plasma performance can still be limited because of the increased level of impurities.

ICRF impurity issue is still an active research topic. The assessment of the impurity issue in the 10 % design of SPARC has been mainly based on experiments on two devices: the field-aligned antenna experiment on C-Mod (Wukitch et al. Reference Wukitch, Garrett, Ochoukov, Terry, Hubbard, Labombard, Lau, Lin, Lipschultz and Miller2013) and the three-strap antenna study on ASDEX Upgrade (Bobkov et al. Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016). The SPARC antenna design will incorporate the insights from the two experiments.

It had been long postulated that the ICRF impurity problem is related to the rf sheath that is generated by the slow waves propagating along the magnetic field lines connected to material surfaces. In the rf sheath region, plasma ions are accelerated to high speed and then sputtering occurs if the ion energy is above a certain threshold. The oscillating rf current on the antenna straps induces both fast waves and slow waves in the plasma. The E field parallel to the B field is associated with the slow wave. Therefore, if all the antenna current is perpendicular to the magnetic field, slow waves can be eliminated. One way towards achieving that is by rotating the antenna to let the antenna straps perpendicular to the magnetic field for the typical tokamak operation. Such a field-aligned antenna would be better than the conventional toroidal aligned antenna in terms of impurities.

On Alcator C-Mod, a field-aligned four-strap antenna (FA-J antenna) was installed and its characteristic in impurity generation was studied by comparing to other conventional antennae (D and E antennae). The main results have been reported by Wukitch et al. (Reference Wukitch, Garrett, Ochoukov, Terry, Hubbard, Labombard, Lau, Lin, Lipschultz and Miller2013). Supported by strong experimental evidence, the field-aligned antenna indeed has lower impurity level than the traditional toroidal aligned antennae at the same antenna power density and plasma conditions. However, the physics behind the result may not be all a result of the reduced rf sheath. In some experimental measurements, the sheath was not much lower. Other mechanisms, for example, modified E × B convective cells in front of the antenna, may also help control the impurity transport. One other benefit of the field-aligned antenna is the antenna load tolerance. As mentioned in § 3, the antenna load is different in L-mode, H-mode and ELMs. The variation of the loading of the FA-J antenna under different plasma conditions is much smaller than that of the D and E antennae partly because some common-mode variation is cancelled out by maintaining symmetry along the field line. SPARC antennae will use the field-aligned scheme (e.g. rotated by ~10°) to have better control of impurity sources and be less demanding for the design of the transmission line matching network with less variation in loading.

On ASDEX Upgrade, experiments on a three-strap antenna have shown to be promising in reducing impurities (Bobkov et al. Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016). The central strap of the three-strap antenna is wider than the two outer straps and is run with higher rf power. The antenna has been shown to generate much lower level of impurities than typical two-strap antennae at the same total rf power. The main mechanism is thought to be the modification of image current (induced by the rf current on the antenna straps) on the antenna frame so that the local rf sheath has been reduced, which leads to lower impurity generation. In the last campaign on Alcator C-Mod, experiments were carried out to mimic the ASDEX Upgrade three-strap antenna operation by reconfiguring the field-aligned four-strap antenna by connecting the two inner straps to the same transmitter and the two outer straps to a different transmitter. Such configuration allowed the antenna to run with varied power ratio for P_inner/P_total. In figure 9, the impurity level (using a spectroscopic line viewing the antenna as proxy) is plotted versus the power ratio of P_inner/P_total. In the experiment, P_total was kept constant versus time while the ratio is ramped up and down. Interestingly, the impurity level is shown to have a trough for P_inner/P_total = 0.55–0.8, suggesting that more rf power from the inner straps can indeed have lower impurity generation at the same P_total. This observation broadly agrees with the experimental result from ASDEX Upgrade.

Figure 9. Experiments on C-Mod with varied power from central two-straps versus outer two-straps on the FA-J antenna.

One plausible interpretation of the C-Mod result is that the antenna ${k_\parallel }$ spectrum is improved by the re-arrangement of the antenna power between the inner straps and outer straps. For a normal equal-power operation of the four straps, the antenna ${k_\parallel }$ spectrum, computed by Fourier transformation, would have significant power in the side lobes. The Fourier transformation is done using the toroidal circle as the periodic boundary and assuming uniform current density distribution on each current strap. For simplicity, the image current on the antenna frame is not considered. As shown in figure 10, more power in the two inner straps would launch more power to the main lobes with ${k_\parallel }$ of the desired value. In math terms, it is similar to the effect of a window function for Fourier transformation. As mentioned in §§ 2 and 3, antenna ${k_\parallel }$ affects both core absorption and edge coupling. For the power residing in the side lobe with smaller $|{k_\parallel }|$, the ${k_\parallel }$ is too small for effective core absorption, whereas for the power in the side lobe close to twice the main lobe, the ${k_\parallel }$ is too large for edge coupling. As a result, the rf power from the side lobes in the ${k_\parallel }$ spectrum either leaks out of the plasma owing to poor core absorption or stays out of the plasma owing to poor penetration. In other words, both side lobes can have significant contributions to impurity generation. As shown in figure 10, for the configuration of inner and outer straps of the four-strap antenna, the side lobes would be minimized at P_inner/P_outer = 0.67, broadly in agreement with the observation in figure 9. Therefore, for the control of impurity sources, it is better to have the antennae with optimized main lobe ${k_\parallel }$ for both core power absorption and edge coupling, and in operation, with the minimized undesired side lobes in the antenna spectra.

Figure 10. Antenna spectra at different power ratio of P_inner/P_total of the four-strap FA-J antenna on C-Mod. Here P_inner is power to the two central straps.

On the other hand, the power ratio to minimize the excitation of the side lobes on C-Mod approximately corresponds to the minimum of the excited parallel currents at the antenna frame on ASDEX Upgrade. Minimizing the image current on the antenna frame and optimizing the antenna spectra may have produced good result in parallel. The relative importance of the effects depends on the exact antenna geometry (e.g. antenna frame design and plasma limiters). In the next SPARC antenna design stage, multi-dimensional realistic antenna model will be used to optimize the antenna spectrum and to minimize the image current.

The power density per antenna also plays a role for the impurity issue. For the rf sheath to generate impurities, the ions accelerated by the sheath voltage needs to exceed a threshold energy before any wall material sputtering can occur. Sheath voltage is decided by many parameters, including local plasma parameters, but, in general, it is proportional to the magnitude of E field of the slow wave, i.e., proportional to antenna power P ^1/2 for a given antenna geometry. Therefore, the impurity level may be kept low if each individual antenna is run at such a low power level that the rf sheath voltage is below the sputtering threshold. This is true from anecdotal experiences on Alcator C-Mod that the impurity level would become an important issue when rf power per antenna strap >0.5 MW. Unfortunately, having more antennae to reduce antenna power density means more cost, and there are some other mechanisms for impurity generation that are proportional to the total rf power (e.g. fast waves not absorbed in the first pass and then leaked to the wall), and these mechanisms may not be reduced by distributing rf power to more antennae. To design the antenna system for SPARC, we need to have trade-off between the total costs of the antennae and to minimize the impurity level, especially at high total rf power operation.

In summary, to deal with the increased impurity level at high-power ICRF heating, the best option for antennae is field-aligned four-strap antennae with flexibility of spectrum tailoring or field-aligned three-strap antennae, and to have as many antennae as practical to reduce power density per antenna (≤0.5 MW per antenna strap). Further discussion on the antenna as part of the integrated design is given in § 5.

5. Integrated design for ICRF system on SPARC

The physics studies in this report are aiming at determining the basic requirements for the SPARC ICRF system, including transmitters, transmission lines and antennae.

For the choice of the transmitters, rf frequency, bandwidth and maximum power per transmitter need to be determined. RF frequency has been set to be ~120 MHz: the fundamental ³He cyclotron frequency and the second harmonic cyclotron frequency for T at 12 T. It is also the fundamental H IC and the second harmonic D IC at reduced field operation of 8 T. As shown in § 2, these IC resonances will be utilized in heating the SPARC plasma in different scenarios. R&D are carried out, in collaboration with the industries, for tetrodes that can power ≥2 MW at 120 MHz and VSWR ≤1.3. Tetrodes with power output up to 1.8 MW at 131 MHz has been reported in Moriyama et al. (Reference Moriyama, Ogawa, Fujii, Anno, Shinozahi, Terakado, Kimura, Saigusa, Nagashima and Ohta1992). As the performance of tetrodes is typically better at lower frequency (~1/f ²), no showstopper in power tube technology is expected to meet the SPARC requirement. Megawatt-level rf systems from combining solid-state amplifiers are also under consideration. The maximum power requirement for each transmitter will be determined by the power per antenna and the antenna feeding configuration (i.e. how many current straps are connected to one transmitter).

Transmission lines on SPARC will be mostly standard. The relevant physics issue for the design of the transmission line and matching network is the characteristic of the expected antenna load, including the value of the load, the range of load variation and the maximum rate of the variation within a plasma shot and variation for different operational scenarios. According to the estimate in § 3, running 0.5–0.6 MW power per antenna strap would not exceed the empirical V_max limit in the system. The more stringent requirement for the transmission line is the real-time matching capability during L–H transitions and during large ELMs. Assuming that the load variation on SPARC is similar to that on C-Mod, real-time matching using fast ferrite tuners, conjugated T design plus real-time phase shifter (mechanical shifter or via small frequency feedback) will have adequate coverage for all operational scenarios. If frequency feedback is used for the matching network, a bandwidth of the order of ±1 MHz for the transmitters will be sufficient.

The physics studies set strong constraints on the antenna concepts. Wave absorption physics, edge coupling physics and impurities physics all affect the antenna design but in different ways. The optimal ${k_\parallel }$ for wave absorption is to the high end of 10–20 m⁻¹ whereas the optimal ${k_\parallel }$ for edge coupling is to the low end of the range. A value from 15 to 18 m⁻¹ appears to be a good trade-off. The ${k_\parallel }$ value in the main lobe of the antenna spectrum is determined by the phase difference and the arrangement scheme of the current straps, therefore the choice of ${k_\parallel }$ strongly influences the antenna toroidal dimension. In addition to the constraints posed by physics, total power requirement, operational reliability, system cost, maintainability and the number of ports dedicated to ICRF heating all need to be considered. To achieve the total ICRF power and given the constraints of maximum power per antenna for reliable operation, we need to carefully arrange the ports for the antennae in the integrated SPARC device design. In table 1, three low-field-side antenna concepts (A/B/C) are compared. The high-field-side antenna concept was explored early on, but later was discarded owing to the increased complexity in the integration with the device design. For all the antenna concepts shown in the table, we plan to use end-fed and centre-grounded straps such as the D/E antennae on C-Mod to have high operational robustness and rotated ~10° to align with the B field for impurity reduction similar to the FA J antenna on C-Mod.

Table 1. Comparison of antenna concepts.

Concept (A) is a two-strap antenna operated at the standard [0, ${\rm \pi}$] phase. For the present SPARC V2 port with horizontal width of 550 mm, a field-aligned two-strap antenna (strap width ~10 cm, gap between straps ~10 cm, with peak ${k_\parallel }\sim 15\,{\textrm{m}^{ - 1}}$) can fit the port and be moved in and out for maintenance. Similar to the D and E antennae on C-Mod with expected power handling 1.2 MW per antenna, 20 such 2-strap antennae can meet the SPARC heating requirement. Each 2-strap antenna can be fed by one 2 MW transmitter and 20 antennae requires 20 transmitters. The antenna total height is ~35 cm before rotation (strap height ~λ/10 plus antenna top and bottom frames). Each SPARC port can have two antennae, one just above the mid-plane and one just below the mid-plane. For this scheme, 10 of total 18 mid-plane ports will be dedicated to the ICRF antennae. The potential issue of concept (A) is that the antenna spectrum is fixed and there is no knob that can be used for impurity mitigation if impurity should become an issue at high-power operation.

Concept (B) is a three-strap antenna running at [0, ${\rm \pi}$, 0] phase. A layout of such a three-strap antenna, same height as concept (A), is shown in figure 11(a). The antenna strap widths are strap 1 = 7.5 cm, strap 2 = 15 cm, strap 3 = 7.5 cm, gap between straps = 5 cm and total antenna width ~50 cm. It can fit the 550 mm port and create the peak ${k_\parallel }$ around 18 m⁻¹. As shown in figure 11(b), if run with more power from the centre strap, P ₂/(P ₁ + P ₃) > 1, there is less power to the harmonics in the spectrum and according to Bobkov et al. (Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016) also less image current on the antenna frame. The spectrum is calculated using the same way as that in figure 10. This setup can have lower impurity level at a given total antenna power. If the centre strap runs 0.6 MW and P ₂/(P ₁ + P ₃) = 2, the total antenna power would be 0.9 MW, and total 28 antennae and 14 ports are needed. The three-strap antenna can be fed by two 2-MW transmitters or by a single 2-MW transmitter. If the three-strap antenna is powered by two transmitters, P ₂/(P ₁ + P ₃) can be varied continuously so that the optimal power ratio can be determined. However, using two transmitters per antenna for all antennae would be too costly and has very low resource utilization. If each of the three-strap antennae is fed by one transmitter, using special transmission line configuration (e.g. hybrid couplers for power splitting) can achieve the approximate target power ratio among straps and provide total power of 1.2 MW per antenna.

Figure 11. (a) Layout of a three-antenna concept with straps labelled as 1, 2 and 3; (b) antenna spectra with two different power ratios.

Concept (C) is a four-strap antenna similar to the field-aligned J antenna on C-Mod except that the straps are end-fed centre-grounded. With a strap width of 8 cm and centre-to-centre 18.5 cm and same height as concept (A), this antenna produces peak ${k_\parallel }\sim 17.5\,{\textrm{m}^{ - 1}}$. It can have all the features that have been proven on the C-Mod: control of impurity sources, spectrum optimization, as shown in figure 12(b), power and voltage handling, load tolerance, etc. With expected power handling ≥2 MW per antenna, 12 antennae (24 transmitters) in 6 ports would be adequate. Concept (C) requires the fewest ports dedicated to rf heating. One risk factor of this concept is that these antennae are too wide to insert through the standard port and must be mounted in-vessel. Thus, remote maintenance after D–T operation on such an antenna would be significantly more challenging than for the two- and three-strap antennae, which are more easily installed and removed directly through the ports.

Figure 12. (a) Layout of a four-antenna concept with straps labelled as 1, 2, 3 and 4; (b) antenna spectra with two different power ratios.

The antenna spectra shown in the previous analysis were calculated from one antenna. With 12 antennae located at 6 toroidal locations (periodically placed), the combined ${k_\parallel }$ spectrum will be affected by the relative phases of the antennae. If they would all be phase locked, the spectrum would be composed of all sixth harmonics but similar to that of one antenna. If some phase variations among the antennae are allowed, the phase variations would add small-scale features but not change the location of the main peaks in the ${k_\parallel }$ spectrum. As a result, although some engineering challenges arise from issues such as arc detection and transmitters decoupling when running all the antennae simultaneously, the power coupling to the plasma and power absorption would not be affected.

Each antenna concept has its pros and cons. Two-strap antennae are the simplest to manufacture and fit the port, but they lack the knobs for the control of impurity sources and the number of ports is large. Three-strap antennae can fit the port, have the knobs for the control of impurity sources, but they have low power density and require the largest number of antennae and ports. Four-strap antennae have reasonable power density per antenna, have been shown in C-Mod for good control of impurity sources, require the fewest number of antennae and number of ports, but they are too large in size to fit the port and need to be installed in-vessel. After carefully considering the physics, engineering and potential antenna failure modes, we plan to design and manufacture 12 4-strap antennae (using 6 ports) and install them in-vessel as the baseline. The detailed antenna dimensions will be adjusted in the engineering design stage to incorporate other considerations. We will also design insertable three-strap antennae to be ready for manufacture as a backup. The four-strap antennae will be operated in reduced field D–D plasmas and all potential issues will be checked. Because the D–T operation may require less total auxiliary heating power than the D–D operation, there is room for some failure of the four-strap antennae. If concerns arise that the four-strap antennae might not be adequate to provide enough power for the D–T operation, we will manufacture and install three-strap antennae in spare ports for additional heating.

6. Future work and summary

The ICRF wave–plasma physics, rf engineering and tokamak device design are integrated for SPARC. Along with rf engineering focused studies, more critical physics studies need to be carried out for the final ICRF system design.

For the core wave physics, the power absorption among the species for the D(³He) and D–T(³He) heating and the power partition versus plasma global parameters needs to be further modelled. Tuning of ICRF scenarios to create tail energies for fuel ions to maximize the D–T burn rate will be explored, e.g., varying the energetic particle distribution and re-arranging power absorption of different physics mechanisms. The dynamics of the energetic ions in minority heating and the main fusion ions need to be further modelled so that we may have more precise answers on how much energy the fast ions carry and how they slow down to the thermal ions. For example, a tritium tail may only have a small effect on power partition, but perhaps a larger effect on fusion gain. Within the typical SPARC operational scenarios, there are other ICRF heating mechanisms that may be used for specific physics studies, for example, mode conversion heating, fast wave direct electron heating and three-ion heating (Kazakov et al. Reference Kazakov, Ongena, Wright, Wukitch, Lerche, Mantsinen, Van Eester, Craciunescu, Kiptily and Lin2017). Although not critical for the SPARC mission, it will be helpful knowing how and under what conditions we can implement these different heating methods. Possible Alfvén activities from the ICRF wave–particle interaction are described by Scott et al. (Reference Scott, Kramer, Snicker, Varje, Särkimäki, Tolman, Rodriguez-Fernandez and Wright2020).

A better assessment on the antenna load will be carried out based on data-mining of the C-Mod data, recent experimental results from other tokamak and antenna models. As mentioned in § 3, the value of the antenna load influences the power density for antenna, and the load difference and variation influence the design of the transmission line matching network. Operating antennae at very high neutral pressure on C-Mod appears to be an issue, and this needs to be addressed on SPARC.

There are other particular issues related to ICRF antennae on SPARC that need to be addressed. Neutron effects (damage on antennae and neutron shielding) will be considered in antenna material choice and detailed port and feedthrough design. SPARC is not a long-pulse device, therefore the total neutron fluence and potential neutron damage pose fewer constraints than those on ITER and reactors. On the other hand, the expected large force from disruptions will need to be carefully addressed in antenna design.

A research plan needs to be developed for the initial reduced-field operation so that most issues related to the ICRF system can be resolved before entering the first full-field D–T campaign. Note that the antenna edge coupling, antenna power and voltage handling, transmission line matching network and power absorption via minority heating can all be addressed at 8 T operation. To ensure the reliability of operation in D–T, the reliability and potential failure mode of the four-strap antennae need to be fully assessed at 8 T operation.

In summary, ICRF heating will be the sole auxiliary heating method on SPARC. The physics studies for the 10 % SPARC design have shown that the core wave power absorption will be excellent, power coupling at the edge is adequate and solutions are available for the impurity problem. The result of the physics study has provided guidance and constraints on the system design, e.g., transmitter power, transmission line and antenna concepts. Further physics studies will be carried out to help finalize the ICRF system design on SPARC.