Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T15:34:50.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle-in-cell simulations of the relaxation of electron beams in inhomogeneous solar wind plasmas

Published online by Cambridge University Press:  29 November 2016

Jonathan O. Thurgood  and
David Tsiklauri
Jonathan O. Thurgood*
Affiliation:
Department of Mathematics, Physics and Electrical Engineering, Northumbria University, Newcastle upon Tyne NE1 8ST, UK
David Tsiklauri
Affiliation:
School of Physics and Astronomy, Queen Mary University of London, Mile End Road, London E1 4NS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous theoretical considerations of electron beam relaxation in inhomogeneous plasmas have indicated that the effects of the irregular solar wind may account for the poor agreement of homogeneous modelling with the observations. Quasi-linear theory and Hamiltonian models based on Zakharov’s equations have indicated that when the level of density fluctuations is above a given threshold, density irregularities act to de-resonate the beam–plasma interaction, restricting Langmuir wave growth on the expense of beam energy. This work presents the first fully kinetic particle-in-cell (PIC) simulations of beam relaxation under the influence of density irregularities. We aim to independently determine the influence of background inhomogeneity on the beam–plasma system, and to test theoretical predictions and alternative models using a fully kinetic treatment. We carry out one-dimensional (1-D) PIC simulations of a bump-on-tail unstable electron beam in the presence of increasing levels of background inhomogeneity using the fully electromagnetic, relativistic EPOCH PIC code. We find that in the case of homogeneous background plasma density, Langmuir wave packets are generated at the resonant condition and then quasi-linear relaxation leads to a dynamic increase of wavenumbers generated. No electron acceleration is seen – unlike in the inhomogeneous experiments, all of which produce high-energy electrons. For the inhomogeneous experiments we also observe the generation of backwards-propagating Langmuir waves, which is shown directly to be due to the refraction of the packets off the density gradients. In the case of higher-amplitude density fluctuations, similar features to the weaker cases are found, but also packets can also deviate from the expected dispersion curve in 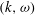$(k,\unicode[STIX]{x1D714})$ -space due to nonlinearity. Our fully kinetic PIC simulations broadly confirm the findings of quasi-linear theory and the Hamiltonian model based on Zakharov’s equations. Strong density fluctuations modify properties of excited Langmuir waves altering their dispersion properties.

Keywords

plasma instabilitiesplasma simulationplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 6 , December 2016 , 905820604
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, R. R., Eastman, T. E., Gurnett, D. A., Frank, L. A. & Parks, G. K. 1981 Plasma waves associated with energetic particles streaming into the solar wind from the earth’s bow shock. J. Geophys. Res. 86, 4493–4510.Google Scholar
Arber, T. D., Bennett, K., Brady, C. S., Lawrence-Douglas, A., Ramsay, M. G., Sircombe, N. J., Gillies, P., Evans, R. G., Schmitz, H., Bell, A. R. et al. 2015 Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 57 (11), 1–26.Google Scholar
Baumgärtel, K. 2013 Coherent amplitude modulation of electron-beam-driven Langmuir waves. Ann. Geophys. 31, 633–638.Google Scholar
Breizman, B. N. & Ryutov, D. D. 1970 Influence of inhomogeneity of plasma on the relaxation of an ultrarelativistic electron beam. Sov. J. Expl Theor. Phys. Lett. 11, 421.Google Scholar
Forslund, D. W., Kindel, J. M., Lee, K., Lindman, E. L. & Morse, R. L. 1975 Theory and simulation of resonant absorption in a hot plasma. Phys. Rev. A 11, 679–683.Google Scholar
Ginzburg, V. L. & Zhelezniakov, V. V. 1958 On the possible mechanisms of sporadic solar radio emission (radiation in an isotropic plasma). Sov. Astron. 2, 653.Google Scholar
Gurnett, D. A., Anderson, R. R., Scarf, F. L. & Kurth, W. S. 1978 The heliocentric radial variation of plasma oscillations associated with type III radio bursts. J. Geophys. Res. 83, 4147–4152.CrossRefGoogle Scholar
Kellogg, P. J., Goetz, K., Monson, S. J. & Bale, S. D. 1999 Langmuir waves in a fluctuating solar wind. J. Geophys. Res. 104, 17069–17078.Google Scholar
Kim, E.-H., Cairns, I. H. & Robinson, P. A. 2007 Extraordinary-mode radiation produced by linear-mode conversion of Langmuir waves. Phys. Rev. Lett. 99 (1), 015003.Google Scholar
Krafft, C., Volokitin, A. S. & Krasnoselskikh, V. V. 2013 Interaction of energetic particles with waves in strongly inhomogeneous solar wind plasmas. Astrophys. J. 778, 111.Google Scholar
Krafft, C., Volokitin, A. S. & Krasnoselskikh, V. V. 2015 Langmuir wave decay in inhomogeneous solar wind plasmas: simulation results. Astrophys. J. 809, 176.Google Scholar
Krafft, C., Volokitin, A. S., Krasnoselskikh, V. V. & de Wit, T. D. 2014 Waveforms of Langmuir turbulence in inhomogeneous solar wind plasmas. J. Geophys. Res. 119, 9369–9382.Google Scholar
Lin, R. P., Potter, D. W., Gurnett, D. A. & Scarf, F. L. 1981 Energetic electrons and plasma waves associated with a solar type III radio burst. Astrophys. J. 251, 364–373.Google Scholar
Lotov, K. V., Timofeev, I. V., Mesyats, E. A., Snytnikov, A. V. & Vshivkov, V. A. 2015 Note on quantitatively correct simulations of the kinetic beam–plasma instability. Phys. Plasmas 22 (2), 024502.Google Scholar
Melrose, D. B. & McPhedran, R. C. 1991 Electromagnetic Processes in Dispersive Media. Cambridge University Press, Cambridge Books Online.CrossRefGoogle Scholar
Muschietti, L., Roth, I. & Ergun, R. E. 1995 Kinetic localization of beam-driven Langmuir waves. J. Geophys. Res. 100, 17481–17490.Google Scholar
Muschietti, L., Roth, I. & Ergun, R. E. 1996 On the formation of wave packets in planetary foreshocks. J. Geophys. Res. 101, 15605–15614.Google Scholar
Nishikawa, K. & Ryutov, D. D. 1976 Relaxation of relativistic electron beam in a plasma with random density inhomogeneities. J. Phys. Soc. Japan 41 (5), 1757–1765.Google Scholar
Pechhacker, R. & Tsiklauri, D. 2014 Three-dimensional particle-in-cell simulation of electron acceleration by Langmuir waves in an inhomogeneous plasma. Phys. Plasmas 21 (1), 012903.Google Scholar
Ratcliffe, H., Brady, C. S., Che Rozenan, M. B. & Nakariakov, V. M. 2014 A comparison of weak-turbulence and particle-in-cell simulations of weak electron–beam plasma interaction. Phys. Plasmas 21 (12), 122104.Google Scholar
Reid, H. A. S. & Ratcliffe, H. 2014 A review of solar type III radio bursts. Res. Astron. Astrophys. 14, 773–804.Google Scholar
Ryutov, D. D. 1969 Quasilinear relaxation of an electron beam in an inhomogeneous plasma. Sov. J. Expl Theor. Phys. 30, 131.Google Scholar
Sturrock, P. A. 1964 Type III solar radio bursts. NASA Special Publication 50, 357.Google Scholar
Thurgood, J. O. & Tsiklauri, D. 2015 Self-consistent particle-in-cell simulations of fundamental and harmonic plasma radio emission mechanisms. Astron. Astrophys. 584, A83.Google Scholar
Torrence, C. & Compo, G. P. 1998 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78.Google Scholar
Voshchepynets, A. & Krasnoselskikh, V. 2013 Electron beam relaxation in inhomogeneous plasmas. Ann. Geophys. 31, 1379–1385.Google Scholar
Voshchepynets, A. & Krasnoselskikh, V. 2015 Probabilistic model of beam–plasma interaction in randomly inhomogeneous solar wind. J. Geophys. Res. 120, 10.Google Scholar
Voshchepynets, A., Krasnoselskikh, V., Artemyev, A. & Volokitin, A. 2015 Probabilistic model of beam–plasma interaction in randomly inhomogeneous plasma. Astrophys. J. 807, 38.Google Scholar
Yoon, P. H. 2011 Asymptotic equilibrium between Langmuir turbulence and suprathermal electrons. Phys. Plasmas 18 (12), 122303.Google Scholar
Yoon, P. H. 2012a Asymptotic equilibrium between Langmuir turbulence and suprathermal electrons in three dimensions. Phys. Plasmas 19 (1), 012304.Google Scholar
Yoon, P. H. 2012b Electron kappa distribution and steady-state Langmuir turbulence. Phys. Plasmas 19 (5), 052301.Google Scholar
Zakharov, V. E., Musher, S. L. & Rubenchik, A. M. 1985 Hamiltonian approach to the description of non-linear plasma phenomena. Phys. Rep. 129, 285–366.Google Scholar