Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T07:29:08.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle trajectories in Weibel magnetic filaments with a flow-aligned magnetic field

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  18 August 2016

Antoine Bret
Antoine Bret*
Affiliation:
ETSI Industriales, Universidad de Castilla-La Mancha, 13071 Ciudad Real, Spain Instituto de Investigaciones Energéticas y Aplicaciones Industriales, Campus Universitario de Ciudad Real, 13071 Ciudad Real, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

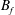For a Weibel shock to form, two plasma shells have to collide and trigger the Weibel instability. At saturation, this instability generates magnetic filaments in the overlapping region with peak field $B_{f}$. In the absence of an external guiding magnetic field, these filaments can block the incoming flow, initiating the shock formation, if their size is larger than the Larmor radius of the incoming particles in the peak field. Here we show that this result still holds in the presence of an external magnetic field 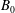$B_{0}$, provided it is not too high. Yet, for 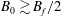$B_{0}\gtrsim B_{f}/2$, the filaments become unable to stop any particle, regardless of its initial velocity.

Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 4 , August 2016 , 905820403
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blandford, R. & Eichler, D. 1987 Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154, 1–75.Google Scholar
Bret, A. 2015 Particles trajectories in magnetic filaments. Phys. Plasmas 22, 072116.CrossRefGoogle Scholar
Bret, A. & Deutsch, C. 2005 Hierarchy of beam plasma instabilities up to high beam densities for fast ignition scenario. Phys. Plasmas 12, 082704.Google Scholar
Bret, A., Dieckmann, M. & Deutsch, C. 2006 Oblique electromagnetic instabilities for a hot relativistic beam interacting with a hot and magnetized plasma. Phys. Plasmas 13, 082109.Google Scholar
Bret, A., Gremillet, L., Bénisti, D. & Lefebvre, E. 2008 Exact relativistic kinetic theory of an electron-beam–plasma system: hierarchy of the competing modes in the system-parameter space. Phys. Rev. Lett. 100, 205008.Google Scholar
Bret, A., Gremillet, L. & Dieckmann, M. E. 2010 Multidimensional electron beam–plasma instabilities in the relativistic regime. Phys. Plasmas 17, 120501.Google Scholar
Bret, A., Stockem, A., Fiúza, F., Ruyer, C., Gremillet, L., Narayan, R. & Silva, L. O. 2013 Collisionless shock formation, spontaneous electromagnetic fluctuations, and streaming instabilities. Phys. Plasmas 20, 042102.Google Scholar
Bret, A., Stockem, A., Narayan, R. & Silva, L. O. 2014 Collisionless Weibel shocks: full formation mechanism and timing. Phys. Plasmas 21 (7), 072301.Google Scholar
Davidson, R. C., Hammer, D. A., Haber, I. & Wagner, C. E. 1972 Nonlinear development of electromagnetic instabilities in anisotropic plasmas. Phys. Fluids 15, 317–333.Google Scholar
Deutsch, C., Bret, A., Firpo, M.-C. & Fromy, P. 2005 Interplay of collisions with quasilinear growth rates of relativistic electron-beam-driven instabilities in a superdense plasma. Phys. Rev. E 72, 026402.Google Scholar
Dieckmann, M. E., Sarri, G., Doria, D., Ahmed, H. & Borghesi, M. 2014 Evolution of slow electrostatic shock into a plasma shock mediated by electrostatic turbulence. New J. Phys. 16, 073001.Google Scholar
Fiuza, F., Fonseca, R. A., Tonge, J., Mori, W. B. & Silva, L. O. 2012 Weibel-instability-mediated collisionless shocks in the laboratory with ultraintense lasers. Phys. Rev. Lett. 108, 235004.Google Scholar
Godfrey, B. B., Shanahan, W. R. & Thode, L. E. 1975 Linear theory of a cold relativistic beam propagating along an external magnetic field. Phys. Fluids 18, 346–355.Google Scholar
Huntington, C. M., Fiuza, F., Ross, J. S., Zylstra, A. B., Drake, R. P., Froula, D. H., Gregori, G., Kugland, N. L., Kuranz, C. C., Levy, M. C. et al. 2015 Observation of magnetic field generation via the Weibel instability in interpenetrating plasma flows. Nat. Phys. 11, 173–176.CrossRefGoogle Scholar
Jackson, J. D. 1998 Classical Electrodynamics. Wiley.Google Scholar
Lyubarsky, Y. & Eichler, D. 2006 Are gamma-ray bursts mediated by the Weibel instability? Astrophys. J. 647, 1250–1254.Google Scholar
Marcowith, A., Bret, A., Bykov, A., Dieckman, M. E., Drury, L. O. C., Lembège, B., Lemoine, M., Morlino, G., Murphy, G., Pelletier, G. et al. 2016 The microphysics of collisionless shock waves. Rep. Prog. Phys. 79, 046901.CrossRefGoogle ScholarPubMed
Medvedev, M. V. & Loeb, A. 1999 Generation of magnetic fields in the relativistic shock of gamma-ray burst sources. Astrophys. J. 526, 697–706.Google Scholar
Milosavljevic, M., Nakar, E. & Spitkovsky, A. 2006 Steady state electrostatic layers from Weibel instability in relativistic collisionless shocks. Astrophys. J. 637, 765–773.Google Scholar
Niemiec, J., Pohl, M., Bret, A. & Wieland, V. 2012 Nonrelativistic parallel shocks in unmagnetized and weakly magnetized plasmas. Astrophys. J. 759 (1), 73 (20 pp).Google Scholar
Novo, A. S., Bret, A., Fonseca, R. A. & Silva, L. O. 2015 Shock formation in electron-ion plasmas: mechanism and timing. Astrophys. J. Lett. 803 (2), L20 (6 pp).Google Scholar
Pathak, V. B., Grismayer, T., Stockem, A., Fonseca, R. A. & Silva, L. O. 2015 Spatial-temporal evolution of the current filamentation instability. New J. Phys. 17 (4), 043049.Google Scholar
Piran, T. 2004 The physics of gamma-ray bursts. Rev. Mod. Phys. 76, 1143–1210.Google Scholar
Sagdeev, R. Z. 1966 Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23–91.Google Scholar
Sarri, G., Dieckmann, M. E., Kourakis, I. & Borghesi, M. 2011 Generation of a purely electrostatic collisionless shock during the expansion of a dense plasma through a rarefied medium. Phys. Rev. Lett. 107, 025003.CrossRefGoogle ScholarPubMed
Schlickeiser, R. & Shukla, P. K. 2003 Cosmological magnetic field generation by the Weibel instability. Astrophys. J. Lett. 599, L57–L60.Google Scholar
Silva, L. O., Fonseca, R. A., Tonge, J. W., Dawson, J. M., Mori, W. B. & Medvedev, M. V. 2003 Interpenetrating plasma shells: near-equipartition magnetic field generation and nonthermal particle acceleration. Astrophys. J. 596, L121–L124.Google Scholar
Silva, L. O., Fonseca, R. A., Tonge, J. W., Mori, W. B. & Dawson, J. M. 2002 On the role of the purely transverse Weibel instability in fast ignitor scenarios. Phys. Plasmas 9, 2458–2461.Google Scholar
Spitkovsky, A. 2005 Simulations of relativistic collisionless shocks: shock structure and particle acceleration. In Astrophysical Sources of High Energy Particles and Radiation (ed. Bulik, T., Rudak, B. & Madejski, G.), American Institute of Physics Conference Series, vol. 801, pp. 345–350.Google Scholar
Stockem, A., Fiuza, F., Bret, A., Fonseca, R. A. & Silva, L. O. 2014 Exploring the nature of collisionless shocks under laboratory conditions. Sci. Rep. 4, 3934.Google Scholar
Stockem, A., Lerche, I. & Schlickeiser, R. 2006 On the physical realization of two-dimensional turbulence fields in magnetized interplanetary plasmas. Astrophys. J. 651, 584–589.Google Scholar
Treumann, R. A. 2009 Fundamentals of collisionless shocks for astrophysical application. Part 1. Non-relativistic shocks. Astron. Astrophys. Rev. 17, 409–535.Google Scholar
Vietri, M., De Marco, D. & Guetta, D. 2003 On the generation of ultra-high-energy cosmic rays in gamma-ray bursts: a reappraisal. Astrophys. J. 592, 378–389.Google Scholar
Zel’dovich, Y. B. & Raizer, Y. P. 2002 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Dover.Google Scholar