1. Introduction
The Wendelstein 7-X (W7-X) stellarator (Klinger et al. Reference Klinger, Andreeva, Bozhenkov, Brandt, Burhenn, Buttenschön, Fuchert, Geiger, Grulke and Laqua2019) is designed for long pulse steady state plasma operation. Hence, the control and improvement of the overall performance is a major task in fusion research. Intrinsic impurities being released from plasma facing components during plasma–wall interaction or released as a product during the fusion reaction can dilute the plasma, degrade the energy confinement and limit accessible operational parameter ranges. The radiation of these impurities in the plasma reduces the plasma temperature and might lead to radiative instabilities. Hence, impurity accumulation has to be avoided since its massive presence can significantly degrade the plasma performance of a fusion device (Ida et al. Reference Ida, Fonck, Sesnic, Hulse and LeBlanc1987). For these reasons, the investigation of the impurity transport is of utmost importance.
There are several studies reporting on impurity confinement in W7-X (Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019; Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020, Reference Langenberg, Wegner, Marchuk, García-Regaña, Pablant, Fuchert, Bozhenkov, Damm, Pasch and Brunner2021; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a; García-Regaña et al. Reference García-Regaña, Barnes, Calvo, Parra, Alcusón, Davies, González-Jerez, Mollén, Sánchez and Velasco2021b), however, these works focus only on individual plasma scenarios without giving an overview considering different plasma conditions. However, in order to achieve a uniform and consistent understanding of impurity behavior, an overview is of great importance and is presented in the following.
After an introduction of the analyzed scenarios and methodology in § 2, the dependence of the impurity confinement behavior on different parameters is presented in the subsequent § 3. Finally, § 4 summarizes the most important results and motivates the further application of the database created in the framework of this work.
2. Analyzed scenarios and methodology
The objective of this study is the characterization and documentation of the core impurity transport at W7-X at a variety of different plasma conditions. Therefore, 52 experimental programs at different plasma parameters are considered in the following. The experiments were performed in the previous operational phase (OP1.2b with uncooled carbon divertor) in two different magnetic field configurations (‘standard’ and ‘high mirror’ labelled as EJM and KJM Andreeva Reference Andreeva2002) using hydrogen as the main fuel gas. In these experimental programs, a total of 123 (64 in EJM and 59 in KJM) non-intrinsic impurity injections were applied by means of the laser blow-off (LBO) system (Wegner et al. Reference Wegner, Geiger, Kunkel, Burhenn, Schröder, Biedermann, Buttenschön, Cseh, Drews and Grulke2018, Reference Wegner, Geiger, Foest, van Vuuren, Winters, Biedermann, Burhenn, Buttenschön, Cseh and Joda2020). In particular, trace amounts of iron (less than $10^{17}$![]() atoms and $n_\mathrm {Fe}/n_\mathrm {e}<10^{-5}$
atoms and $n_\mathrm {Fe}/n_\mathrm {e}<10^{-5}$![]() ) were injected into different plasma scenarios. An overview of the parameter space is shown in figure 1.
) were injected into different plasma scenarios. An overview of the parameter space is shown in figure 1.
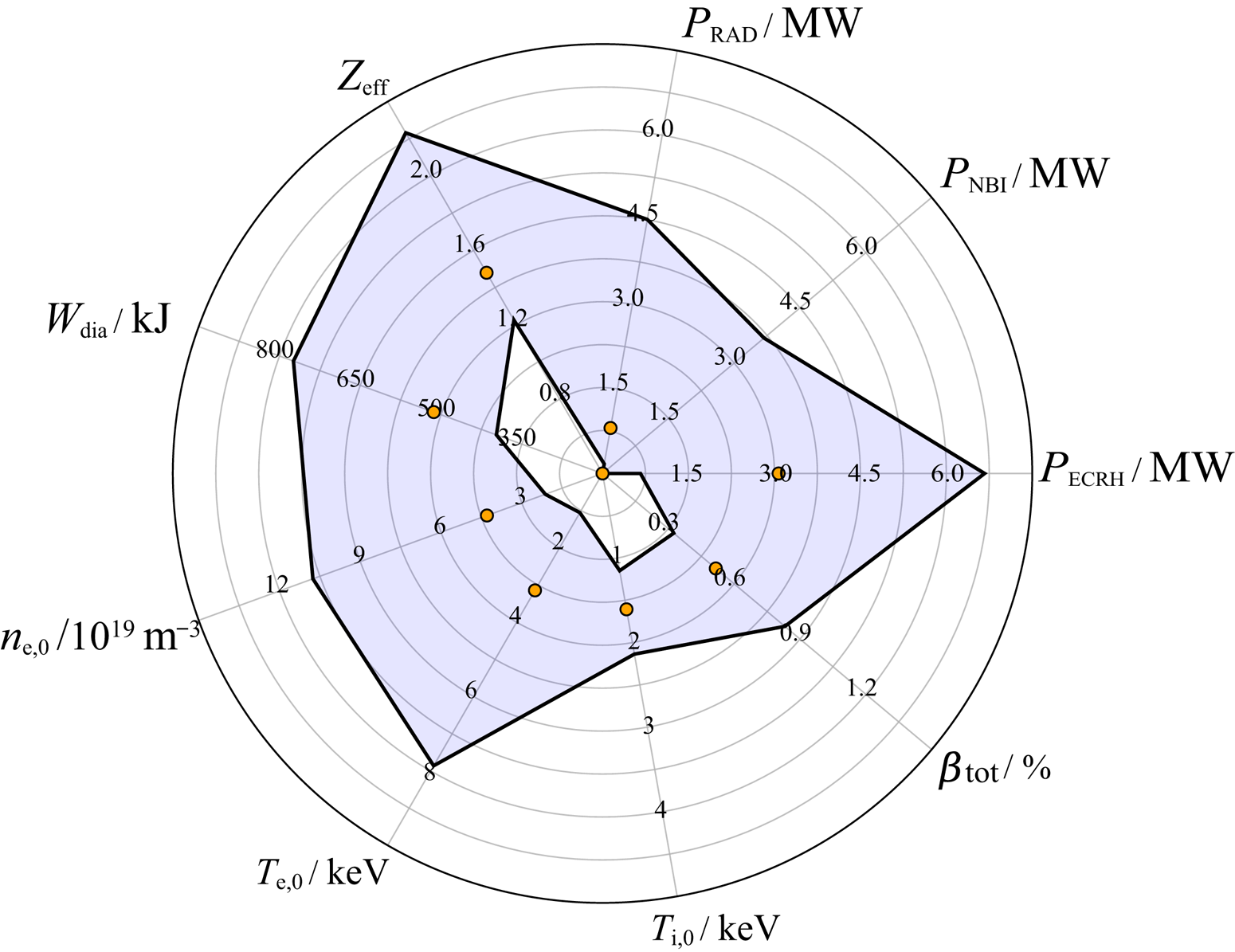
Figure 1. Overview of the parameter space of the ECRH power $P_\mathrm {ECRH}$![]() , NBI heating power $P_\mathrm {NBI}$
, NBI heating power $P_\mathrm {NBI}$![]() , radiated power $P_\mathrm {RAD}$
, radiated power $P_\mathrm {RAD}$![]() , effective ion charge $Z_\mathrm {eff}$
, effective ion charge $Z_\mathrm {eff}$![]() , diamagnetic energy $W_\mathrm {dia}$
, diamagnetic energy $W_\mathrm {dia}$![]() as well as the central values of the electron density $n_{\mathrm {e},0}$
as well as the central values of the electron density $n_{\mathrm {e},0}$![]() , electron temperature $T_{\mathrm {e},0}$
, electron temperature $T_{\mathrm {e},0}$![]() and ion temperature $T_{\mathrm {i},0}$
and ion temperature $T_{\mathrm {i},0}$![]() and the plasma beta $\beta _\mathrm {tot}$
and the plasma beta $\beta _\mathrm {tot}$![]() , respectively. The filled circles within the individual parameter space indicate the median of the interval.
, respectively. The filled circles within the individual parameter space indicate the median of the interval.
It should be emphasized that all of the following conclusions and scaling attempts are based on this database. This database represents the most relevant operational regimes during the considered campaign. However, in order to allow a reliable evaluation of the impurity transport, only experimental programs at stationary conditions are included. Most of them were performed in pure electron cyclotron resonant heated (ECRH) plasmas. In addition, a few discharges with neutral beam injection (NBI) heating of up to 3.5 MW on top of ECRH power are also taken into account for the following analysis.
The methodology consists of studying the impurity transport and its dependence on other quantities to examine transport regimes and allow predictive statements. Hence, the above mentioned impurity injection by means of LBO is evaluated in terms of the impurity transport time $\tau _{I}$![]() , being a measure for the impurity confinement. The transport time is the decay time of the spectroscopic signals in the vacuum ultraviolet (VUV) and X-ray wavelength range, taking into account various charge stages of iron. Additionally, the transport coefficients are inferred by a one-dimensional transport code STRAHL (Behringer Reference Behringer1987). Further details of this analysis are described in the literature (Wegner et al. Reference Wegner, Geiger, Kunkel, Burhenn, Schröder, Biedermann, Buttenschön, Cseh, Drews and Grulke2018; Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a).
, being a measure for the impurity confinement. The transport time is the decay time of the spectroscopic signals in the vacuum ultraviolet (VUV) and X-ray wavelength range, taking into account various charge stages of iron. Additionally, the transport coefficients are inferred by a one-dimensional transport code STRAHL (Behringer Reference Behringer1987). Further details of this analysis are described in the literature (Wegner et al. Reference Wegner, Geiger, Kunkel, Burhenn, Schröder, Biedermann, Buttenschön, Cseh, Drews and Grulke2018; Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a).
Due to experimental and numerical confirmation of a large diffusive turbulent contribution to the impurity transport (e.g. flat impurity profiles) in standard ECRH plasmas (dominant ECRH without kinetic profile shaping events, e.g. pellet injection) (Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019; Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a; García-Regaña et al. Reference García-Regaña, Barnes, Calvo, González-Jerez, Thienpondt, Sánchez, Parra and St-Onge2021a,Reference García-Regaña, Barnes, Calvo, Parra, Alcusón, Davies, González-Jerez, Mollén, Sánchez and Velascob), only the inferred diffusion coefficient is considered in the following study. In particular, the turbulent diffusion profile is inferred using an iterative optimization procedure embedded in STRAHL while the convection profile is set to the classical and neoclassical estimations. A comparable determination of the turbulent convection profile is too inaccurate with the current data situation and, as mentioned above, is not necessary for most of the plasma scenarios presented here.
The following discussion includes not only the transport parameters but also the Thomson scattering data (Pasch et al. Reference Pasch, Beurskens, Bozhenkov, Fuchert, Knauer and Wolf2016), such as the electron density and temperature profiles ($n_\mathrm {e}$![]() , $T_\mathrm {e}$
, $T_\mathrm {e}$![]() ), as well as the measurements from the X-ray imaging spectroscopy (Langenberg et al. Reference Langenberg, Pablant, Marchuk, Zhang, Alonso, Burhenn, Svensson, Valson, Gates and Beurskens2017) with respect to the ion temperature profile ($T_\mathrm {i}$
), as well as the measurements from the X-ray imaging spectroscopy (Langenberg et al. Reference Langenberg, Pablant, Marchuk, Zhang, Alonso, Burhenn, Svensson, Valson, Gates and Beurskens2017) with respect to the ion temperature profile ($T_\mathrm {i}$![]() ). These profiles are used as input to evaluate the classical and neoclassical transport parameters ($D_\mathrm {neo}$
). These profiles are used as input to evaluate the classical and neoclassical transport parameters ($D_\mathrm {neo}$![]() , $v_\mathrm {neo}$
, $v_\mathrm {neo}$![]() ) with the drift kinetic equation solver (DKES) (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986). In addition, the density fluctuation amplitude ($\tilde {n}_\mathrm {e}$
) with the drift kinetic equation solver (DKES) (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986). In addition, the density fluctuation amplitude ($\tilde {n}_\mathrm {e}$![]() ) measured with the phase contrast imaging (PCI) system (Edlund et al. Reference Edlund, Porkolab, Huang, Grulke, Böttger, von Sehren and von Stechow2018) is incorporated into the following discussion. To achieve comparability to other discharges, the density fluctuation amplitude is normalized to the line-integrated electron density.
) measured with the phase contrast imaging (PCI) system (Edlund et al. Reference Edlund, Porkolab, Huang, Grulke, Böttger, von Sehren and von Stechow2018) is incorporated into the following discussion. To achieve comparability to other discharges, the density fluctuation amplitude is normalized to the line-integrated electron density.
3. Results and discussion
The correlation of the transport properties to the above mentioned parameters and the attempt to derive scaling laws from them enables a direct comparison with other machines and allows an extrapolation of the impurity transport in future plasma scenarios.
The behavior of the impurity confinement in terms of dependence on the main plasma parameters is shown in figure 2 using the transport time as a representative. Fortunately, the confinement of impurities in W7-X at moderate densities is fairly weak so far, which is reflected in relatively low transport times of the order of approximately 100 ms. Hence, most experimental programs could be conducted without any impurity accumulation. Nevertheless, there is one program that exhibits higher impurity confinement and for which transport times of up to 1 s have been observed. These are examined and discussed in more detail below.

Figure 2. Impurity transport time over the central electron density (a) and temperature (b) as well as over the ion temperature (c) for the magnetic field configurations ‘standard’ (EJM, $\circ$![]() ) and ‘high mirror’ (KJM, $\square$
) and ‘high mirror’ (KJM, $\square$![]() ). The main heating scheme is visualized with the filling degree of the symbols (half-filled: NBI and ECRH, full: pure ECRH).
). The main heating scheme is visualized with the filling degree of the symbols (half-filled: NBI and ECRH, full: pure ECRH).
At these moderate electron densities, a clear density dependence cannot be observed. However, there seems to be a general correlation between the impurity confinement and the electron temperature as the transport time decreases with higher temperatures. This suggests that the ECRH, which significantly determines the electron temperature, has an influence on the transport behavior. In the following it will be shown that the ECRH determines the level of turbulence. However, there is no clear correlation between the transport time and the core ion temperature. Additionally, there is no obvious difference in the impurity transport between the two magnetic field configurations EJM and KJM. This is particularly true for all parameters presented for comparison and dependency studies. This weak dependence on these two magnetic field configurations is basically expected and supported by theory, assuming the transport is dominated by turbulence (Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020; Navarro et al. Reference Navarro, Merlo, Plunk, Xanthopoulos, von Stechow, Siena, Maurer, Hindenlang, Wilms and Jenko2020; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a). Hence, it is planned to rather compare the magnetic field configurations ‘low’ and ‘high mirror’ since gyro-kinetic simulations presume a significant difference in the turbulent transport (Navarro et al. Reference Navarro, Merlo, Plunk, Xanthopoulos, von Stechow, Siena, Maurer, Hindenlang, Wilms and Jenko2020).
In the following, the dependence on the magnetic field configuration is not further elaborated and presented in the figures. In addition, for the database considered here, no conclusive picture of the influence of heating deposition, plasma beta (plasma pressure normalized to magneticfield), electric field (beside core ion and electron root confinement) or rotational transform could be found, as has been observed in other papers (see the summary in Burhenn et al. Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009). One reason for this could be that the overall statistical analysis of many different plasma scenarios does not allow a direct comparison. For this, one would have to select dedicated experimental programs and investigate them in detail. However, this is not the focus of this paper and will be addressed in future publications. Furthermore, the parameter space and variation for some parameters, e.g. magnetic field strength or minor radius, is not large enough to conduct reliable dependency studies. The NBI heated scenarios are particularly conspicuous in the plots of electron density and ion temperature, see figure 2(a,c).
First, it must be mentioned that the NBI system is generally fuelling (density increase) as well as heating (ion temperature increase). Moreover, it it has been observed that the turbulent transport channel is suppressed in NBI heated plasmas, leading to higher transport times and hence better confinement (Romba et al. Reference Romba, Reimold, Ford, Jaspers, Vanó and Klinger2023). Since the ions are mainly heated via the electron-to-ion energy exchange power and due to the observed high core ion transport, the ion temperature is basically saturated below 2 keV (Beurskens et al. Reference Beurskens, Bozhenkov, Ford, Xanthopoulos, Zocco, Turkin, Alonso, Beidler, Calvo and Carralero2021).
With the electron density, a first rudimentary comparison with other stellarators is possible and is shown in figure 3. In particular, the transport time of impurities is plotted against the line-averaged density. Compared with other machines, again, the density dependence of the transport time for W7-X is rather small. Confinement changes as found for W7-AS at higher densities (transition from H to HDH mode) (Burhenn et al. Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009) could not be observed for W7-X up to now. Nevertheless, the confinement in W7-X is lower compared with the other stellarators above a line-averaged density of $5\times 10^{19}\ \mathrm {m}^{-3}$![]() . In terms of impurities and their potential impact on the overall plasma properties, these are encouraging prospects, despite the fact that the energy confinement is also relatively low.
. In terms of impurities and their potential impact on the overall plasma properties, these are encouraging prospects, despite the fact that the energy confinement is also relatively low.

Figure 3. Impurity transport time over line-averaged density for the stellarators TJ-II$^\star$![]() ($\square$
($\square$![]() ), LHD$^\star$
), LHD$^\star$![]() ($\triangle$
($\triangle$![]() ), W7-AS$^\star$
), W7-AS$^\star$![]() ($\lozenge$
($\lozenge$![]() ) and W7-X ($\circ$
) and W7-X ($\circ$![]() ). The main heating scheme is visualized with the filling degree of the symbols (empty: pure NBI, half-filled: NBI and ECRH, full: pure ECRH). $^\star$
). The main heating scheme is visualized with the filling degree of the symbols (empty: pure NBI, half-filled: NBI and ECRH, full: pure ECRH). $^\star$![]() Data taken from Burhenn et al. (Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009).
Data taken from Burhenn et al. (Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009).
A more detailed view can be obtained by studying the transport behavior and, in particular, by determining the transport coefficients as mentioned in § 2. Obviously, there is a correlation between the transport time and the line-averaged diffusion coefficient, see figure 4. With the help of the inferred diffusion coefficient, the transport regime can be determined by relating it to the neoclassical diffusion values. Taking into account that a purely neoclassical transport leads to transport times of the order of seconds (Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020), the here observed transport times are below the neoclassical estimations. In particular, the observed diffusion coefficient is orders of magnitude larger compared with neoclassical (including classical contribution) expectations. Nevertheless, there seems to be some kind of threshold at a ratio of 100 between the turbulent and neoclassical diffusion. Below a ratio of 100, the transport time increases above 100 ms and the turbulent influence seems to reduce. If the ratio exceeds 100, the transport time decreases below 100 ms down to approximately 50 ms for turbulence enhanced scenarios.

Figure 4. Impurity transport time over the line-averaged turbulent diffusion coefficient (a), the ratio between the turbulent and neoclassical line-averaged diffusion coefficient (b) and the normalized density fluctuation amplitude (c). The main heating scheme is visualized with the filling degree of the symbols (half-filled: NBI and ECRH, full: pure ECRH).
All the above statements on the influence of turbulence on transport behavior have recently been discussed in experimental (Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019; Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a) and theoretical (Helander & Zocco Reference Helander and Zocco2018; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020; Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a; Xanthopoulos et al. Reference Xanthopoulos, Bozhenkov, Beurskens, Smith, Plunk, Helander, Beidler, Alcusón, Alonso and Dinklage2020; García-Regaña et al. Reference García-Regaña, Barnes, Calvo, González-Jerez, Thienpondt, Sánchez, Parra and St-Onge2021a,Reference García-Regaña, Barnes, Calvo, Parra, Alcusón, Davies, González-Jerez, Mollén, Sánchez and Velascob) works. Some experimental programs are compared with respect to their turbulence level (Wegner et al. Reference Wegner, Alcusón, Geiger, von Stechow, Xanthopoulos, Angioni, Beurskens, Böttger, Bozhenkov and Brunner2020a), however, a comprehensive overview is still missing. An overview of the transport time and confinement is shown in figure 4(c) as a function of the density fluctuation level. Similar to electron temperature and diffusion coefficient, the transport time decreases with increasing density fluctuation level, indicating an increased turbulence level. In other words, as the influence of turbulence increases, the impurity confinement diminishes and the transport is enhanced. In particular, the ECRH power appears to have a significant effect on the turbulence level and ultimately on the impurity confinement, although other mechanisms are also important. Figure 5 clearly shows the influence of the ECRH power on the transport time (a) and on the line-averaged diffusion coefficient (b). With increasing heating power, the transport time decreases and the impurity confinement becomes worse, because the turbulence is enhanced, leading to increased turbulent diffusion coefficients. With decreasing ECRH power, the confinement improves as the turbulence is reduced and the transport time increases, the diffusion coefficients are also lower compared with the turbulence enhanced scenario.

Figure 5. Impurity transport time (a) and the line-averaged turbulent (b) over the ECRH power. The main heating scheme is visualized with the filling degree of the symbols (half-filled: NBI and ECRH, full: pure ECRH).
The impact of other mechanisms on the impurity confinement will be elaborated in future publications. Especially, the impact of turbulence drivers like the normalized density or temperature gradient length as well as the impact of the electric field will be the focus of upcoming publications. In particular, the scenario with a transport time of approximately 1 s is examined in more detail. With the help of large-scale nonlinear gyro-kinetic simulations, it could be shown that density peaking is the reason for the suppression of turbulence, which leads to a significantly better confinement behavior (Alcusón et al. Reference Alcusón, Wegner, Dinklage, Langenberg, Bähner, Buttenschön, Edlund, Fuchert, García-Regaña and Grulke2023).
Since the level of turbulence strongly regulates the impurity confinement, an overview of the parameter space for the turbulence reduced and enhanced plasma scenarios is given in figure 6. For simplicity, the boundary between these two scenarios is defined here by the transport time. Plasmas with an impurity transport time above 100 ms are assigned to the turbulence reduced scenario, while plasmas with a transport time less than or equal to 100 ms are assigned to the turbulence enhanced scenario. This threshold was selected because the assumption of a completely diffusive transport up to 100 ms transport time is best fulfilled. Further investigations have shown that, above this limit, a convective part is more difficult to neglect. Unfortunately, the current data situation does not allow us to determine the convective part of the transport. Nevertheless, this leads to results that describe the experiments well, although the error bars are somewhat larger for plasmas with better impurity confinement.

Figure 6. Overview of the parameter space of the ECRH power $P_\mathrm {ECRH}$![]() , NBI heating power $P_\mathrm {NBI}$
, NBI heating power $P_\mathrm {NBI}$![]() , radiated power $P_\mathrm {RAD}$
, radiated power $P_\mathrm {RAD}$![]() , effective ion charge $Z_\mathrm {eff}$
, effective ion charge $Z_\mathrm {eff}$![]() , diamagnetic energy $W_\mathrm {dia}$
, diamagnetic energy $W_\mathrm {dia}$![]() , central values of the electron density $n_{\mathrm {e},0}$
, central values of the electron density $n_{\mathrm {e},0}$![]() , electron temperature $T_{\mathrm {e},0}$
, electron temperature $T_{\mathrm {e},0}$![]() and ion temperature $T_{\mathrm {i},0}$
and ion temperature $T_{\mathrm {i},0}$![]() , plasma beta as well as the line-averaged diffusion coefficient. The light blue area represents the whole parameter space as it is shown in figure 1 extended by the diffusion coefficient (median indicated with filled cirlces). The light red area indicates the parameter space for the turbulence reduced scenarios (median indicated with crosses).
, plasma beta as well as the line-averaged diffusion coefficient. The light blue area represents the whole parameter space as it is shown in figure 1 extended by the diffusion coefficient (median indicated with filled cirlces). The light red area indicates the parameter space for the turbulence reduced scenarios (median indicated with crosses).
The attempt to derive scaling laws allows an extrapolation of the impurity transport in future plasma scenarios. Initially, an existing scaling law from W7-AS (Burhenn et al. Reference Burhenn, Hacker, Ledl, Unger, Baldzuhn, Hofmann and Weller1995) as the predecessor of W7-X was examined for purely ECRH plasma scenarios as the ECRH power $P_\mathrm {ECRH}$![]() is considered only. That scaling law also takes into account the central electron density $n_{\mathrm {e},0}$
is considered only. That scaling law also takes into account the central electron density $n_{\mathrm {e},0}$![]() , minor radius $a$
, minor radius $a$![]() and the magnetic field strength on axis, $B_0$
and the magnetic field strength on axis, $B_0$![]() . Unfortunately, the parameter space for the minor radius as well magnetic field strength is limited so that no reliable conclusion can be made from this. To derive a reliable scaling law, the data are additionally checked for possible collinearities. The result of that scaling attempt taking into account the database described in § 2 is shown in figure 7. The respective fit parameters and hence the impact strength of the parameter on the confinement behavior are listed in table 1. As already mentioned above, the impact of the ECRH power on the impurity confinement is confirmed also by the scaling attempt in which the exponent of the power is relatively high in absolute value. Additionally, the low exponent of 0.2 is the result of the weak density dependence, as discussed above. Another scaling attempt, which takes into account the drivers for the ion temperature gradient driven turbulent transport, points in the right direction, but cannot yet be shown here because the profile information of the main plasma parameters have to be revised to make trustworthy statements. This will be a topic of future publications.
. Unfortunately, the parameter space for the minor radius as well magnetic field strength is limited so that no reliable conclusion can be made from this. To derive a reliable scaling law, the data are additionally checked for possible collinearities. The result of that scaling attempt taking into account the database described in § 2 is shown in figure 7. The respective fit parameters and hence the impact strength of the parameter on the confinement behavior are listed in table 1. As already mentioned above, the impact of the ECRH power on the impurity confinement is confirmed also by the scaling attempt in which the exponent of the power is relatively high in absolute value. Additionally, the low exponent of 0.2 is the result of the weak density dependence, as discussed above. Another scaling attempt, which takes into account the drivers for the ion temperature gradient driven turbulent transport, points in the right direction, but cannot yet be shown here because the profile information of the main plasma parameters have to be revised to make trustworthy statements. This will be a topic of future publications.

Figure 7. Impurity transport time over its value inferred with the scaling law. The axis diagonal is plotted as dotted line.
Table 1. List of fit parameters of the scaling law $\tau =C\times P_\mathrm {ECRH}^\alpha \times n_{\mathrm {e},0}^\beta \times a^\gamma \times B_0^\delta$![]() for W7-AS taken from Burhenn et al. (Reference Burhenn, Hacker, Ledl, Unger, Baldzuhn, Hofmann and Weller1995) and for W7-X.
for W7-AS taken from Burhenn et al. (Reference Burhenn, Hacker, Ledl, Unger, Baldzuhn, Hofmann and Weller1995) and for W7-X.

4. Summary and conclusion
The impurity transport of W7-X under different plasma conditions has been characterized and documented using a database approach. The dependence on plasma parameters has been investigated. Compared with other stellarators, W7-X has only a weak correlation to the electron density. The ECRH power, which also defines the core electron temperature, influences the confinement behavior, which is mainly turbulence dominated. The neoclassical optimization of W7-X (Beidler et al. Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Bozhenkov, Brunner, Damm and Drevlak2021) enables a unique opportunity to observe and document the presence of this turbulent contribution to the overall impurity transport. This is additionally confirmed by scaling attempts taking into account several parameters. This allows an extrapolation of the impurity transport in future plasma scenarios.
The observations shown here are only the beginning and the study of the influence of other parameters will be possible and presented in other publications. In addition, this database will be expanded with data from future campaigns, which will allow monitoring of trends and the integration of other parameters, boundary conditions and magnetic field configurations.
Acknowledgements
Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Editor Cary Forest thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 - EUROfusion).







































