Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T20:56:19.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Overstability of plasma slow electron holes

Published online by Cambridge University Press:  28 February 2022

I.H. Hutchinson Open the ORCID record for I.H. Hutchinson [Opens in a new window]
I.H. Hutchinson*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Sufficient conditions are found on the ion velocity distribution 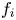$f_i$ and potential amplitude for stability of steady electron holes moving at slow speeds, coinciding with the bulk of 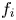$f_i$. Fully establishing stability requires calculation of the ion response to shift potential perturbations having an entire range of oscillatory frequencies, because under some conditions real frequencies intermediate between the ion and electron responses prove to be unstable even when the extremes are not. The mechanism of this overstability is explained and calculated in detail. Electron holes of peak potential 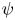$\psi$ less than approximately 0.01 times the background temperature (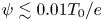$\psi \lesssim 0.01T_0/e$) avoid the oscillatory instability entirely. For them, the necessary condition that there be a local minimum in 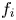$f_i$ in which the hole resides is also sufficient, unless the magnetic field 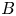$B$ is low enough to permit the transverse instability having finite wavenumber 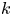$k$ perpendicular to 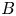$B$.

Keywords

plasma instabilitiesplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 555880101
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Eliasson, B. & Shukla, P.K. 2004 Dynamics of electron holes in an electron-oxygen-ion plasma. Phys. Rev. Lett. 93 (4), 45001.CrossRefGoogle Scholar
Eliasson, B. & Shukla, P.K. 2006 Formation and dynamics of coherent structures involving phase-space vortices in plasmas. Phys. Rep. 422 (6), 225–290.CrossRefGoogle Scholar
Graham, D.B., Khotyaintsev, Y.V., Vaivads, A. & André, M. 2016 Electrostatic solitary waves and electrostatic waves at the magnetopause. J. Geophys. Res.: Space Phys. 121, 3069–3092.CrossRefGoogle Scholar
Hutchinson, I.H. 2017 Electron holes in phase space: what they are and why they matter. Phys. Plasmas 24 (5), 055601.CrossRefGoogle Scholar
Hutchinson, I.H. 2018 Transverse instability of electron phase-space holes in multi-dimensional Maxwellian plasmas. J. Plasma Phys. 84, 905840411.CrossRefGoogle Scholar
Hutchinson, I.H. 2019 a Electron phase-space hole transverse instability at high magnetic field. J. Plasma Phys. 85 (5), 905850501.CrossRefGoogle Scholar
Hutchinson, I.H. 2019 b Transverse instability magnetic field thresholds of electron phase-space holes. Phys. Rev. E 99, 053209.CrossRefGoogle ScholarPubMed
Hutchinson, I.H. 2021 a Asymmetric one-dimensional slow electron holes. Phys. Rev. E 104, 055207.CrossRefGoogle ScholarPubMed
Hutchinson, I.H. 2021 b How can slow plasma electron holes exist? Phys. Rev. E 104, 015208.CrossRefGoogle ScholarPubMed
Kamaletdinov, S.R., Hutchinson, I.H., Vasko, I.Y., Artemyev, A., Lotekar, A. & Mozer, F. 2021 Spacecraft observations and theoretical understanding of slow electron holes. Phys. Rev. Lett. 127, 165101.CrossRefGoogle ScholarPubMed
Lotekar, A., Vasko, I.Y., Mozer, F.S., Hutchinson, I., Artemyev, A.V., Bale, S.D., Bonnell, J.W., Ergun, R., Giles, B., Khotyaintsev, Y.V., et al. 2020 Multisatellite mms analysis of electron holes in the earth's magnetotail: origin, properties, velocity gap, and transverse instability. J. Geophys. Res.: Space Phys. 125 (9), e2020JA028066.CrossRefGoogle Scholar
Muschietti, L., Roth, I., Ergun, R.E. & Carlson, C.W. 1999 Analysis and simulation of BGK electron holes. Nonlinear Process. Geophys. 6 (3/4), 211–219.CrossRefGoogle Scholar
Parlett, B.N. 1974 The Rayleigh quotient iteration and some generalizations for nonnormal matrices. Maths Comput. 28 (127), 679–693.CrossRefGoogle Scholar
Saeki, K. & Rasmussen, J.J. 1991 Stationary solution of coupled electron hole and ion soliton in a collisionless plasma. J. Phys. Soc. Japan 60 (3), 735–738.CrossRefGoogle Scholar
Steinvall, K., Khotyaintsev, Y.V., Graham, D.B., Vaivads, A., Lindqvist, P.-A., Russell, C.T. & Burch, J.L. 2019 Multispacecraft analysis of electron holes. Geophys. Res. Lett. 46 (1), 55–63.CrossRefGoogle Scholar
Zhou, C. & Hutchinson, I.H. 2016 Plasma electron hole kinematics. II. Hole tracking particle-in-cell simulation. Phys. Plasmas 23 (8), 82102.CrossRefGoogle Scholar
Zhou, C. & Hutchinson, I.H. 2017 Plasma electron hole ion-acoustic instability. J. Plasma Phys. 83, 90580501.Google Scholar
Zhou, C. & Hutchinson, I.H. 2018 Dynamics of a slow electron hole coupled to an ion-acoustic soliton. Phys. Plasmas 25 (8), 082303.CrossRefGoogle Scholar