Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T15:55:55.309Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-local energy transfer via zonal flow in the Dimits shift

Part of: Focus on Fusion

Published online by Cambridge University Press:  10 October 2017

Denis A. St-Onge Open the ORCID record for Denis A. St-Onge [Opens in a new window]
Denis A. St-Onge*
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA Princeton Plasma Physics Laboratory, P.O. Box 451, Princeton, NJ 08543, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The two-dimensional Terry–Horton equation is shown to exhibit the Dimits shift when suitably modified to capture both the nonlinear enhancement of zonal/drift-wave interactions and the existence of residual Rosenbluth–Hinton states. This phenomenon persists through numerous simplifications of the equation, including a quasilinear approximation as well as a four-mode truncation. 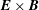It is shown that the use of an appropriate adiabatic electron response, for which the electrons are not affected by the flux-averaged potential, results in an $\boldsymbol{E}\times \boldsymbol{B}$ nonlinearity that can efficiently transfer energy non-locally to length scales of the order of the sound radius. The size of the shift for the nonlinear system is heuristically calculated and found to be in excellent agreement with numerical solutions. The existence of the Dimits shift for this system is then understood as an ability of the unstable primary modes to efficiently couple to stable modes at smaller scales, and the shift ends when these stable modes eventually destabilize as the density gradient is increased. This non-local mechanism of energy transfer is argued to be generically important even for more physically complete systems.

Keywords

fusion plasmaplasma instabilitiesplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 5 , October 2017 , 905830504
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beer, M. A. & Hammett, G. W. 1999 The dynamics of small-scale turbulence-driven flows. In Proceedings of the Joint Varenna-Lausanne Int. Workshop on Theory of Fusion Plasmas, Varenna, 1998 (ed. Connor, J. W., Sindoni, E. & Vaclavik, J.), p. 19. Societa Italiana di Fisica.Google Scholar
Biglari, H., Diamond, P. H. & Terry, P. W. 1990 Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B 2 (1), 1–4.Google Scholar
Burrell, K. H. 1997 Effects of $\boldsymbol{E}\boldsymbol{\times }\boldsymbol{B}$ velocity shear and magnetic shear on turbulence and transport in magnetic confinement devices. Phys. Plasmas 4 (5), 1499–1518.Google Scholar
Carter, T. A. & Maggs, J. E. 2009 Modifications of turbulence and turbulent transport associated with a bias-induced confinement transition in the large plasma device. Phys. Plasmas 16 (1), 012304.Google Scholar
Connaughton, C. P., Nadiga, B. T., Nazarenko, S. V. & Quinn, B. E. 2010 Modulational instability of Rossby and drift waves and generation of zonal jets. J. Fluid Mech. 654, 207–231.Google Scholar
Cowley, S. C., Kulsrud, R. M. & Sudan, R. 1991 Considerations of ion-temperature-gradient-driven turbulence. Phys. Fluids B 3 (10), 2767–2782.Google Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 Zonal flows in plasma – a review. Plasma Phys. Control. Fusion 47 (5), R35.Google Scholar
Dimits, A. M., Bateman, G., Beer, M. A., Cohen, B. I., Dorland, W., Hammett, G. W., Kim, C., Kinsey, J. E., Kotschenreuther, M., Kritz, A. H. et al. 2000 Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 7 (3), 969–983.Google Scholar
Dimits, A. M., Cohen, B. I., Mattor, N., Nevins, W. M., Shumaker, D. E., Parker, S. E. & Kim, C.1999 Simulation of ion-temperature-gradient turbulence in tokamaks. In Proceedings of the Seventeenth International Conference on Plasma Physics and Controlled Nuclear Fusion Research, Yokahama, Japan, 1998. International Atomic Energy Agency.Google Scholar
Dorland, W. & Hammett, G. W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B 5 (3), 812–835.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 2009 A stochastic structural stability theory model of the drift wave–zonal flow system. Phys. Plasmas 16 (11), 112903.Google Scholar
Guzdar, P. N., Kleva, R. G. & Chen, L. 2001 Shear flow generation by drift waves revisited. Phys. Plasmas 8 (2), 459–462.Google Scholar
Hammett, G. W., Beer, M. A., Dorland, W., Cowley, S. C. & Smith, S. A. 1993 Developments in the gyrofluid approach to tokamak turbulence simulations. Plasma Phys. Control. Fusion 35, 973.Google Scholar
Hatch, D. R., Terry, P. W., Jenko, F., Merz, F. & Nevins, W. M. 2011 Saturation of gyrokinetic turbulence through damped eigenmodes. Phys. Rev. Lett. 106, 115003.Google Scholar
Holland, C., Diamond, P. H., Champeaux, S., Kim, E., Gurcan, O., Rosenbluth, M. N., Tynan, G. R., Crocker, N., Nevins, W. & Candy, J. 2003 Investigations of the role of nonlinear couplings in structure formation and transport regulation: experiment, simulation, and theory. Nucl. Fusion 43 (8), 761.CrossRefGoogle Scholar
Itoh, K., Itoh, S.-I., Diamond, P. H., Hahm, T. S., Fujisawa, A., Tynan, G. R., Yagi, M. & Nagashima, Y. 2006 Physics of zonal flows. Phys. Plasmas 13 (5), 055502.CrossRefGoogle Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7 (5), 1904–1910.Google Scholar
Kolesnikov, R. A. & Krommes, J. A. 2005a Transition to collisionless ion-temperature-gradient-driven plasma turbulence: a dynamical systems approach. Phys. Rev. Lett. 94, 235002.Google Scholar
Kolesnikov, R. A. & Krommes, J. A. 2005b Bifurcation theory of the transition to collisionless ion-temperature-gradient-driven plasma turbulence. Phys. Plasmas 12 (12), 122302.CrossRefGoogle Scholar
Krommes, J. A. & Kim, C.-B. 2000 Interactions of disparate scales in drift-wave turbulence. Phys. Rev. E 62, 8508–8539.Google Scholar
Liang, Y.-M., Diamond, P. H., Wang, X.-H., Newman, D. E. & Terry, P. W. 1993 A two-nonlinearity model of dissipative drift wave turbulence. Phys. Fluids B 5 (4), 1128–1139.Google Scholar
Lin, Z., Hahm, T. S., Lee, W. W., Tang, W. M. & Diamond, P. H. 1999 Effects of collisional zonal flow damping on turbulent transport. Phys. Rev. Lett. 83, 3645–3648.Google Scholar
Makwana, K. D., Terry, P. W. & Kim, J.-H. 2012 Role of stable modes in zonal flow regulated turbulence. Phys. Plasmas 19 (6), 062310.CrossRefGoogle Scholar
Makwana, K. D., Terry, P. W., Pueschel, M. J. & Hatch, D. R. 2014 Subdominant modes in zonal-flow-regulated turbulence. Phys. Rev. Lett. 112, 095002.Google Scholar
Mikkelsen, D. R. & Dorland, W. 2008 Dimits shift in realistic gyrokinetic plasma-turbulence simulations. Phys. Rev. Lett. 101, 135003.Google Scholar
Numata, R., Ball, R. & Dewar, R. L. 2007 Bifurcation in electrostatic resistive drift wave turbulence. Phys. Plasmas 14 (10), 102312.Google Scholar
Ottaviani, M., Beer, M. A., Cowley, S. C., Horton, W. & Krommes, J. A. 1997 Turbulence and intermittency in plasmas unanswered questions in ion-temperature-gradient-driven turbulence. Phys. Rep. 283 (1), 121–146.Google Scholar
Parker, J. B. 2016 Dynamics of zonal flows: failure of wave-kinetic theory, and new geometrical optics approximations. J. Plasma Phys. 82 (6), 595820602.Google Scholar
Parker, J. B. & Krommes, J. A. 2013 Zonal flow as pattern formation. Phys. Plasmas 20 (10), 100703.Google Scholar
Parker, J. B. & Krommes, J. A. 2014 Generation of zonal flows through symmetry breaking of statistical homogeneity. New J. Phys. 16 (3), 035006.Google Scholar
Ricci, P., Rogers, B. N. & Dorland, W. 2006 Small-scale turbulence in a closed-field-line geometry. Phys. Rev. Lett. 97, 245001.Google Scholar
Rogers, B. N., Dorland, W. & Kotschenreuther, M. 2000 Generation and stability of zonal flows in ion-temperature-gradient mode turbulence. Phys. Rev. Lett. 85, 5336.Google Scholar
Rosenbluth, M. N. & Hinton, F. L. 1998 Poloidal flow driven by ion-temperature-gradient turbulence in tokamaks. Phys. Rev. Lett. 80, 724–727.Google Scholar
Ruiz, D. E., Parker, J. B., Shi, E. L. & Dodin, I. Y. 2016 Zonal-flow dynamics from a phase-space perspective. Phys. Plasmas 23 (12), 122304.Google Scholar
Schaffner, D. A., Carter, T. A., Rossi, G. D., Guice, D. S., Maggs, J. E., Vincena, S. & Friedman, B. 2012 Modification of turbulent transport with continuous variation of flow shear in the large plasma device. Phys. Rev. Lett. 109, 135002.Google Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostrophic instability. J. Atmos. Sci. 69 (5), 1633–1656.CrossRefGoogle Scholar
St-Onge, D. A. & Krommes, J. A. 2017 Zonostrophic instability driven by discrete particle noise. Phys. Plasmas 24 (4), 042107.Google Scholar
Tang, W. M. 1978 Microinstability theory in tokamaks. Nucl. Fusion 18 (8), 1089.Google Scholar
Terry, P. W. 2000 Suppression of turbulence and transport by sheared flow. Rev. Mod. Phys. 72, 109–165.Google Scholar
Terry, P. W. & Horton, W. 1982 Stochasticity and the random phase approximation for three electron drift waves. Phys. Fluids 25, 491–501.Google Scholar
Terry, P. W. & Horton, W. 1983 Drift wave turbulence in a low-order $k$ space. Phys. Fluids 26, 106–112.CrossRefGoogle Scholar

St-Onge supplementary material

Movie 1

Download St-Onge supplementary material(Video)
Video 13.5 MB

St-Onge supplementary material

Movie 2

Download St-Onge supplementary material(Video)
Video 11 MB

St-Onge supplementary material

Movie 3

Download St-Onge supplementary material(Video)
Video 23.3 MB