Published online by Cambridge University Press: 10 August 2023
We present a study of subcritical shocks in a highly collisional laboratory plasma with a dynamically significant magnetic field. Shocks were produced by placing cylindrical obstacles into the supermagnetosonic ($M_{{\rm MS}} \sim 1.9$ ) outflow from an inverse wire array z-pinch at the MAGPIE pulsed power facility ($n_{e} \sim 8.5 \times 10^{17}\,{\rm cm}^{-3}$
) outflow from an inverse wire array z-pinch at the MAGPIE pulsed power facility ($n_{e} \sim 8.5 \times 10^{17}\,{\rm cm}^{-3}$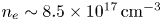 , $v \sim 45\,{\rm km}\,{\rm s}^{-1}$
, $v \sim 45\,{\rm km}\,{\rm s}^{-1}$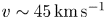 ). We demonstrate the existence of subcritical shocks in this regime and find that secondary stagnation shocks form in the downstream which we infer from interferometry and optical Thomson scattering measurements are hydrodynamic in nature. The subcritical shock width is found to be approximately equal to the resistive diffusion length and we demonstrate the absence of a jump in hydrodynamic parameters. Temperature measurements by collective optical Thomson scattering showed little temperature change across the subcritical shock (${<}10\,\%$
). We demonstrate the existence of subcritical shocks in this regime and find that secondary stagnation shocks form in the downstream which we infer from interferometry and optical Thomson scattering measurements are hydrodynamic in nature. The subcritical shock width is found to be approximately equal to the resistive diffusion length and we demonstrate the absence of a jump in hydrodynamic parameters. Temperature measurements by collective optical Thomson scattering showed little temperature change across the subcritical shock (${<}10\,\%$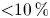 of the ion kinetic energy) which is consistent with a balance between adiabatic and Ohmic heating and radiative cooling. We demonstrate the absence of subcritical shocks when the obstacle diameter is less than the resistive diffusion length due to decoupling of the magnetic field from the plasma. These findings are supported by magnetohydrodynamic simulations using the Gorgon and AstroBEAR codes and discrepancies between the simulations and experiment are discussed.
of the ion kinetic energy) which is consistent with a balance between adiabatic and Ohmic heating and radiative cooling. We demonstrate the absence of subcritical shocks when the obstacle diameter is less than the resistive diffusion length due to decoupling of the magnetic field from the plasma. These findings are supported by magnetohydrodynamic simulations using the Gorgon and AstroBEAR codes and discrepancies between the simulations and experiment are discussed.