Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T13:54:44.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-turbulent electric fields in soliton and shock-like structures in magnetized plasmas

Published online by Cambridge University Press:  13 March 2009

C. W. Mendel  and
T. P. Wright
C. W. Mendel
Affiliation:
Sandia Laboratories, Albuquerque, New Mexico
T. P. Wright
Affiliation:
Sandia Laboratories, Albuquerque, New Mexico
Get access Rights & Permissions [Opens in a new window]

Abstract

A new treatment of soliton and laminar shock-like structures in single ion species and counter-streaming plasmas in perpendicular magnetic fields is presented. Charge separation effects are treated exactly, and may become important for high Alfvén Mach number flows. The theory contains the familiar quasi-neutrality theory in the limit B20 ≪ Μ0nmec2 and the Longmire theory in the limit B20 ≫ Μ0nmec2. The introduction of the potential ψ as the primary dependent variable, instead of the magnetic field B, clarifies the role of ion dynamics. New pseudo-potential functions are defined which generate classes of solutions for single ion species, rigid piston problems, and multispecies problems. They also provide information about the evolution of particle piston solutions. Results include the fact that a small amount of resistivity allows shock solutions for very large Mach numbers, and for zero dissipation the parameter

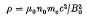
does not affect the solutions except in the scale length.

Type
Research Article
Information
Journal of Plasma Physics , Volume 10 , Issue 1 , August 1973 , pp. 149 - 164
Copyright
Copyright © Cambridge University Press 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adlam, J. & Allen, J. 1958 Phil. Mag. 3, 448.CrossRefGoogle Scholar
Auer, P. & Evers, W. Jr 1971 Phys. Fluids, 14, 1177.CrossRefGoogle Scholar
Auer, P., Hruwitz, H. Jr & Kilb, R. 1961 Phys. Fluids, 4, 1105.CrossRefGoogle Scholar
Auer, P., Hurwitz, H. Jr & Kilb, R. 1962 Phys. Fluids, 5, 298.CrossRefGoogle Scholar
Coffey, T. P. 1970 Phys. Fluids, 13, 1249.CrossRefGoogle Scholar
Davis, L., Löst, R. & Schluter, A. 1958 Z. Naturforsch. A 13, 916.CrossRefGoogle Scholar
De Silva, A. W., Dove, W. F., Spalding, I. J. & Goldenbaum, , 1971 Phys. Fluids, 14, 42.Google Scholar
Eskov, A. G., Kurtmulirev, R. Kh., Malyutin, A. I., Pilskii, B. I. & Semenov, V. N. 1969 Zh. Eksp. Teor. Fiz. 56, 1480.Google Scholar
Longmire, C. L. 1963 Elementary Plasma Physics. Interscienee.Google Scholar
Manheimer, W. M. & Flynn, R. 1971 Phys. Rev. Lett. 27, 1175.Google Scholar
Mendel, C. W. & Wright, T. P. 1972 Bull. Am. Phys. Soc. 17, 100.Google Scholar
Rossow, V. 1965 Phys. Fluids, 8, 358.CrossRefGoogle Scholar
Sagdeev, R. Z. 1966 Reviews in Plasma Physics, vol.4 (ed. Leontovich, M. A.). NewYork: Consultants Bureau.Google Scholar
Tidman, D. A. & Krall, N. A. 1971 Shock Waves in Collisionless Plasmas. Interscience.CrossRefGoogle Scholar
Vandervoort, P. 1960 Ann. Phys. 10, 401.CrossRefGoogle Scholar
Widner, M. M. & Wright, T. P. 1972 Phys. Rev. Lett. 28, 1179.Google Scholar
Woods, L. C. 1971 Plasma Phys. 13, 885.CrossRefGoogle Scholar
Wright, T. P. 1971 Phys. Fluids, 14, 1905.CrossRefGoogle Scholar