Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T16:33:10.188Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-modal onset of the tearing instability

Published online by Cambridge University Press:  18 September 2018

D. MacTaggart Open the ORCID record for D. MacTaggart [Opens in a new window]
D. MacTaggart*
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow G12 8QQ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the onset of the classical magnetohydrodynamic (MHD) tearing instability (TI) and focus on non-modal (transient) growth rather than the tearing mode. With the help of pseudospectral theory, the operators of the linear equations are shown to be highly non-normal, resulting in the possibility of significant transient growth at the onset of the TI. This possibility increases as the Lundquist number 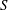$S$ increases. In particular, we find evidence, numerically, that the maximum possible transient growth, measured in the 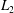$L_{2}$-norm, for the classical set-up of current sheets unstable to the TI, scales as 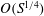$O(S^{1/4})$ on time scales of 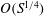$O(S^{1/4})$ for 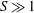$S\gg 1$. This behaviour is much faster than the time scale 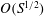$O(S^{1/2})$ when the solution behaviour is dominated by the tearing mode. The size of transient growth obtained is dependent on the form of the initial perturbation. Optimal initial conditions for the maximum possible transient growth are determined, which take the form of wave packets and can be thought of as noise concentrated at the current sheet. We also examine how the structure of the eigenvalue spectrum relates to physical quantities.

Keywords

plasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 5 , October 2018 , 905840501
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhattacharjee, A., Huang, Y.-M., Yang, H. & Rogers, B. 2009 Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16, 112102.Google Scholar
Birn, J., Drake, J. F., Shay, M. A., Rogers, B. N, Denton, R. E., Hesse, M., Kuznetsova, M., Ma, Z. W., Bhattacharjee, A., Otto, A. et al. 2001a Geospace enviromential modelling (GEM) magnetic reconnection challenge. J. Geophys. Res. 106, 3715.Google Scholar
Birn, J. & Hesse, M. 2001b Geospace environment modelling (GEM) magnetic reconnection challenge: resistive tearing, anisotropic pressure and Hall effects. J. Geophys. Res. 106, 3737.Google Scholar
Borba, D., Riedel, K. S., Kerner, W., Huysmans, G. T. A., Ottaviani, M. & Schmid, P. J. 1994 The pseudospectrum of the resistive magnetohydrodynamics operator: resolving the resistive Alfvén paradox. Phys. Plasmas 1, 3151.Google Scholar
Bourne, D. P. 2003 Hydrodynamic stability, the Chebyshev tau method and spurious eigenvalues. Contin. Mech. Thermodyn. 15, 571.Google Scholar
Chen, L., Herreman, W., Li, K., Livermore, P. W., Luo, J. W. & Jackson, A. 2018 The optimal kinematic dynamo driven by steady flow in a sphere. J. Fluid Mech. 839, 1.Google Scholar
Dahlburg, R. B. 1994 On the ideal initial value problem for the neutral sheet. Phys. Plasmas 1, 3053.Google Scholar
Dahlburg, R. B., Zang, T. A., Montgomery, D. & Hussaini, M. Y. 1983 Viscous, resistive magnetohydrodynamic stability computed by spectral methods. Proc. Natl Acad. Sci. USA 80, 5798.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1999a Optimal exitation of magnetic fields. Astrophys. J. 522, 1079.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1999b Stochastic dynamics of field generation in conducting fluids. Astrophys. J. 522, 1088.Google Scholar
Furth, H. P., Kileen, J. & Rosenbluth, M. N. 1963 Finite-resitivity instabilities of a sheet pinch. Phys. Fluids 6, 459.Google Scholar
Golub, G. H. & Van Loan, C. F. 1996 Matrix Computations, 3rd ed. John Hopkins University Press.Google Scholar
Goedbloed, J. P., Keppens, R. & Poedts, S. 2010 Advanced Magnetohydrodynamics. Cambridge University Press.Google Scholar
Hanifi, A., Schmid, P. J. & Henningson, D. S. 1996 Transient growth in compressible boundary layer flow. Phys. Fluids 8, 826.Google Scholar
Harris, E. G. 1962 On a plasma sheath separating regions of oppositely directed magnetic field. Nuovo Cimento 23, 115.Google Scholar
Huang, Y.-M., Comisso, L. & Bhattacharjee, A. 2017 Plasmoid instability in evolving current sheets and onset of fast reconnection. Astrophys. J. 84, 75.Google Scholar
Kerner, W. 1998 Large-scale complex eigenvalue problems. J. Comput. Phys. 85, 1.Google Scholar
Landremann, M., Plunk, G. G. & Dorland, W. 2015 Generalized universal instability: transient linear amplification and subcritical turbulence. J. Plasma Phys. 81, 905810501.Google Scholar
Livermore, P. W. & Jackson, A. 2006 Transient magnetic energy growth in spherical stationary flows. Proc. R. Soc. Lond. A 462, 2457.Google Scholar
Loureiro, N. F., Schekochihin, A. A. & Cowley, S. C. 2007 Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14, 100703.Google Scholar
MacTaggart, D. & Stewart, P. 2017 Optimal energy growth in current sheets. Solar Phys. 292, 148.Google Scholar
Newton, S. L., Cowley, S. C. & Loureiro, N. F. 2010 Understanding the effect of sheared flow on microinstabilities. Plasma Phys. Control. Fusion 52, 125001.Google Scholar
Obrist, D. & Schmid, P. J. 2010 Algebraically decaying modes and wave packet pseudo-modes in swept Hiemenz flow. J. Fluid Mech. 643, 309.Google Scholar
Pucci, F. & Velli, M. 2014 Reconnection of quasi-singular current sheets: the ‘ideal’ tearing mode. Astrophys. J. 780, L19.Google Scholar
Reddy, S. C., Schmid, P. J. & Henningson, D. S. 1993 Pseudospectra of the Orr–Sommerfield Operator. SIAM J. Appl. Maths 53, 15.Google Scholar
Riedel, K. S. 1986 The spectrum of resistive viscous magnetohydrodynamics. Phys. Fluids 29, 1093.Google Scholar
Samtaney, R., Loureiro, N. F., Uzdensky, D. A., Schekochihin, A. A. & Cowley, S. C. 2009 Formation of plasmoid chains in magnetic reconnection. Phys. Rev. Lett. 103, 105004.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Squire, J. & Bhattacharjee, A. 2014a Nonmodal growth of the magnetorotational instability. Phys. Rev. Lett. 113, 025006.Google Scholar
Squire, J. & Bhattacharjee, A. 2014b Magnetorotational instability: nonmodal growth and the relationship of global modes to the shearing box. Astrophys. J. 797, 67.Google Scholar
Stewart, P. S., Waters, S. L., Billingham, J. & Jensen, O. 2009 Spatially localised growth within global instabilities of flexible channel flow. In Proceedings of the Seventh IUTAM Symposium on Laminar-Turbulent Transition, IUTAM Bookseries, vol. 18, p. 397. Springer.Google Scholar
Tenerani, A., Velli, M, Pucci, F., Landi, S. & Rappazzo, A. F. 2016 ‘Ideally’ unstable current sheets and the triggering of fast magnetic reconnection. J. Plasma Phys. 82, 535820501.Google Scholar
Trefethen, L. N. 1999 Computation of pseudospectra. Acta Numer. 8, 247.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: The Behaviour of Non-normal Matrices and Operators. Princeton University Press.Google Scholar
van Wyk, F., Highcock, E. G., Schekochihin, A. A., Roach, C. M., Field, A. R. & Dorland, W. 2016 Transition to subcritical turbulence in a tokamak plasma. J. Plasma Phys. 82, 905820609.Google Scholar
Uzdensky, D. A. & Loureiro, N. F. 2016 Magnetic reconnection onset via disruption of a forming current sheet by the tearing instability. Phys. Rev. Lett. 116, 105003.Google Scholar
Vanneste, J. & Byatt-Smith, J. G. 2007 Fast scalar decay in a shear flow: modes and pseudomodes. J. Fluid Mech. 572, 219.Google Scholar
Wright, T. G.2002 EigTool. http://www.comlab.ox.ac.uk/pseudospectra/eigtool/.Google Scholar