1 Introduction
Turbulence plays an important role in facilitating particle energization and plasma heating in space and astrophysical plasmas, influencing the macroscopic evolution of many poorly understood systems, such as the solar corona and solar wind, planetary magnetospheres and black hole accretion disks. The turbulent cascade mediates the transfer of energy from magnetic fields and plasma flows at large scales down to much smaller scales where dissipation mechanisms can effectively remove energy from the turbulent fluctuations, ultimately converting that energy to plasma heat. Understanding the details of this nonlinear turbulent cascade to small scales and of the mechanisms by which the turbulent energy is thermalized represents a grand challenge problem in heliophysics and astrophysics.
Early research on incompressible magnetohydrodynamics (MHD) turbulence in the 1960s (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965) suggested that nonlinear interactions between counterpropagating Alfvén waves – or Alfvén wave collisions – support the turbulent cascade of energy from large to small scales. Following significant previous studies on weak incompressible MHD turbulence (Sridhar & Goldreich Reference Sridhar and Goldreich1994; Montgomery & Matthaeus Reference Montgomery and Matthaeus1995; Ng & Bhattacharjee Reference Ng and Bhattacharjee1996; Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000), recent work has elucidated the mechanism of energy transfer in Alfvén wave collisions in the weakly nonlinear limit by computing an asymptotic analytical solution using incompressible MHD (Howes & Nielson Reference Howes and Nielson2013), verifying that solution using nonlinear gyrokinetic simulations in the MHD limit,
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$
, of perpendicular scales
$k_{\bot }$
larger than the ion Larmor radius
$\unicode[STIX]{x1D70C}_{i}$
(Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013), and confirming the results experimentally in the laboratory (Howes et al.
Reference Howes, Drake, Nielson, Carter, Kletzing and Skiff2012, Reference Howes, Nielson, Drake, Schroeder, Skiff, Kletzing and Carter2013; Drake et al.
Reference Drake, Schroeder, Howes, Kletzing, Skiff, Carter and Auerbach2013, Reference Drake, Schroeder, Shanken, Howes, Skiff, Kletzing, Carter and Dorfman2014, Reference Drake, Howes, Rhudy, Terry, Carter, Kletzing, Schroeder and Skiff2016). The derivation of the analytical solution was possible using the idealized initial conditions of two overlapping, perpendicularly polarized Alfvén waves in a periodic geometry, and solving for the nonlinear evolution of the system. For initial plane Alfvén waves with wavevectors
$\boldsymbol{k}_{1}^{+}=k_{\bot }\hat{\boldsymbol{x}}-k_{\Vert }\hat{\boldsymbol{z}}$
and
$\boldsymbol{k}_{1}^{-}=k_{\bot }\hat{\boldsymbol{y}}+k_{\Vert }\hat{\boldsymbol{z}}$
, the nonlinear energy transfer is mediated by a nonlinearly generated, purely magnetic mode with wavevector
$\boldsymbol{k}_{2}^{(0)}=k_{\bot }\hat{\boldsymbol{x}}+k_{\bot }\hat{\boldsymbol{y}}$
, which can be interpreted as an oscillating shear in the magnetic field along which the Alfvén waves propagate (Maron & Goldreich Reference Maron and Goldreich2001; Howes & Bourouaine Reference Howes and Bourouaine2017). The nonlinear interaction between
$\boldsymbol{k}_{1}^{\pm }$
and
$\boldsymbol{k}_{2}^{(0)}$
yields a secular transfer of energy from the
$\boldsymbol{k}_{1}^{+}$
Alfvén wave to an Alfvén wave with
$\boldsymbol{k}_{3}^{+}=2k_{\bot }\hat{\boldsymbol{x}}+k_{\bot }\hat{\boldsymbol{y}}-k_{\Vert }\hat{\boldsymbol{z}}$
, and from the
$\boldsymbol{k}_{1}^{-}$
Alfvén wave to an Alfvén wave with
$\boldsymbol{k}_{3}^{-}=k_{\bot }\hat{\boldsymbol{x}}+2k_{\bot }\hat{\boldsymbol{y}}+k_{\Vert }\hat{\boldsymbol{z}}$
. Since the energy is transferred to an Alfvén wave with a higher perpendicular wavenumber,
$|\boldsymbol{k}_{3_{\bot }}^{\pm }|>|\boldsymbol{k}_{1\bot }^{\pm }|$
, this interaction represents the fundamental mechanism by which turbulence transfers energy from larger to smaller scales.
Another important discovery about plasma turbulence followed from the finding that the nonlinear evolution of MHD turbulence simulations leads to the development of intermittent current sheets (Matthaeus & Montgomery Reference Matthaeus and Montgomery1980; Meneguzzi, Frisch & Pouquet Reference Meneguzzi, Frisch and Pouquet1981), and that the dissipation of turbulent energy is found to be largely concentrated in the vicinity of these intermittent current sheets (Uritsky et al. Reference Uritsky, Pouquet, Rosenberg, Mininni and Donovan2010; Osman et al. Reference Osman, Matthaeus, Greco and Servidio2011; Zhdankin et al. Reference Zhdankin, Uzdensky, Perez and Boldyrev2013). This finding has motivated significant recent efforts to seek evidence of the spatial localization of plasma heating by the dissipation of turbulence in current sheets through statistical analyses of solar wind observations (Borovsky & Denton Reference Borovsky and Denton2011; Osman et al. Reference Osman, Matthaeus, Greco and Servidio2011, Reference Osman, Matthaeus, Wan and Rappazzo2012; Perri et al. Reference Perri, Goldstein, Dorelli and Sahraoui2012; Wang et al. Reference Wang, Tu, He, Marsch and Wang2013; Wu et al. Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Osman et al. Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan2014) and numerical simulations (Wan et al. Reference Wan, Matthaeus, Karimabadi, Roytershteyn, Shay, Wu, Daughton, Loring and Chapman2012; Karimabadi et al. Reference Karimabadi, Roytershteyn, Wan, Matthaeus, Daughton, Wu, Shay, Loring, Borovsky and Leonardis2013; TenBarge & Howes Reference TenBarge and Howes2013; Wu et al. Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Zhdankin et al. Reference Zhdankin, Uzdensky, Perez and Boldyrev2013). Although these works clearly demonstrate a connection between current sheets and plasma heating, the origin of these current sheets in plasma turbulence remains unknown: do they represent advected flux tube boundaries (Borovsky Reference Borovsky2008, Reference Borovsky2010), or are they generated dynamically by the turbulence itself (Boldyrev et al. Reference Boldyrev, Perez, Borovsky and Podesta2011; Zhdankin et al. Reference Zhdankin, Boldyrev, Mason and Perez2012)? A significant breakthrough on this question was the discovery that Alfvén wave collisions in the strong turbulence limit naturally generate current sheets (Howes Reference Howes2016), making a connection for the first time between the nonlinear mechanism governing the transfer of energy to small scales and the self-consistent development of intermittent current sheets.
The analytical solution for energy transfer in weak Alfvén wave collisions (Howes & Nielson Reference Howes and Nielson2013) and the simulations showing that strong Alfvén wave collisions naturally generate current sheets (Howes Reference Howes2016) were based on an idealized initial condition in which two finite-amplitude plane Alfvén waves are initially overlapping in a periodic geometry before they begin to interact nonlinearly. Here we eliminate the unrealistic aspect of those studies by simulating the strong nonlinear interactions between two initially separated Alfvén wavepackets, with the aim of determining whether the general properties of Alfvén wave collisions found in the idealized case persist in this more realistic case of colliding wavepackets. Specifically, we focus here on answering two questions: (i) do collisions between Alfvén wavepackets still mediate the transfer of energy to small perpendicular scales?; and (ii) do Alfvén wavepacket collisions in the strongly nonlinear limit still lead to the development of intermittent current sheets? A companion paper (Verniero & Howes Reference Verniero and Howes2018) will investigate whether the nonlinearly generated
$(k_{x}/k_{\bot },k_{y}/k_{\bot },k_{z}/k_{\Vert })=(1,1,0)$
mode still mediates the energy transfer in the weakly collisional limit of Alfvén wavepacket collisions.
In § 2, we describe the set-up of this strong, localized Alfvén wavepacket collision simulation. The nonlinear evolution of this simulation is analysed in § 3, with particular emphasis on the perpendicular cascade of energy in § 3.1, current sheet development in § 3.2, evolution of the energy in § 3.3 and general qualitative properties of localized Alfvén wavepacket collisions in § 3.4. Conclusions are presented in § 4.
2 Simulation
Here we employ the astrophysical gyrokinetics code AstroGK (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010) to perform a gyrokinetic simulation of the nonlinear interaction between two initially separated, counterpropagating Alfvén wavepackets in the strongly nonlinear limit.
AstroGK evolves the perturbed gyroaveraged distribution function
$h_{s}(x,y,z,\unicode[STIX]{x1D706},\unicode[STIX]{x1D700})$
for each species
$s$
, the scalar potential
$\unicode[STIX]{x1D711}$
, the parallel vector potential
$A_{\Vert }$
and the parallel magnetic field perturbation
$\unicode[STIX]{x1D6FF}B_{\Vert }$
according to the gyrokinetic equation and the gyroaveraged Maxwell’s equations (Frieman & Chen Reference Frieman and Chen1982; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). Velocity space coordinates are defined by the pitch angle
$\unicode[STIX]{x1D706}=v_{\bot }^{2}/v^{2}$
and energy
$\unicode[STIX]{x1D700}=v^{2}/2$
. The domain is a periodic box of size
$L_{\bot }^{2}\times L_{z}$
, elongated along the straight, uniform mean magnetic field
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
, where all quantities may be rescaled to any parallel dimension satisfying
$L_{z}/L_{\bot }\gg 1$
. Uniform Maxwellian equilibria for ions (protons) and electrons are chosen, with a realistic mass ratio
$m_{i}/m_{e}=1836$
, where
$m_{i}$
and
$m_{e}$
are the masses of an ion and an electron, respectively. Spatial dimensions
$(x,y)$
perpendicular to the mean field are treated pseudospectrally; an upwind finite-difference scheme is used in the parallel direction,
$z$
. Collisions employ a fully conservative, linearized collision operator with energy diffusion and pitch-angle scattering (Abel et al.
Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al.
Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009).
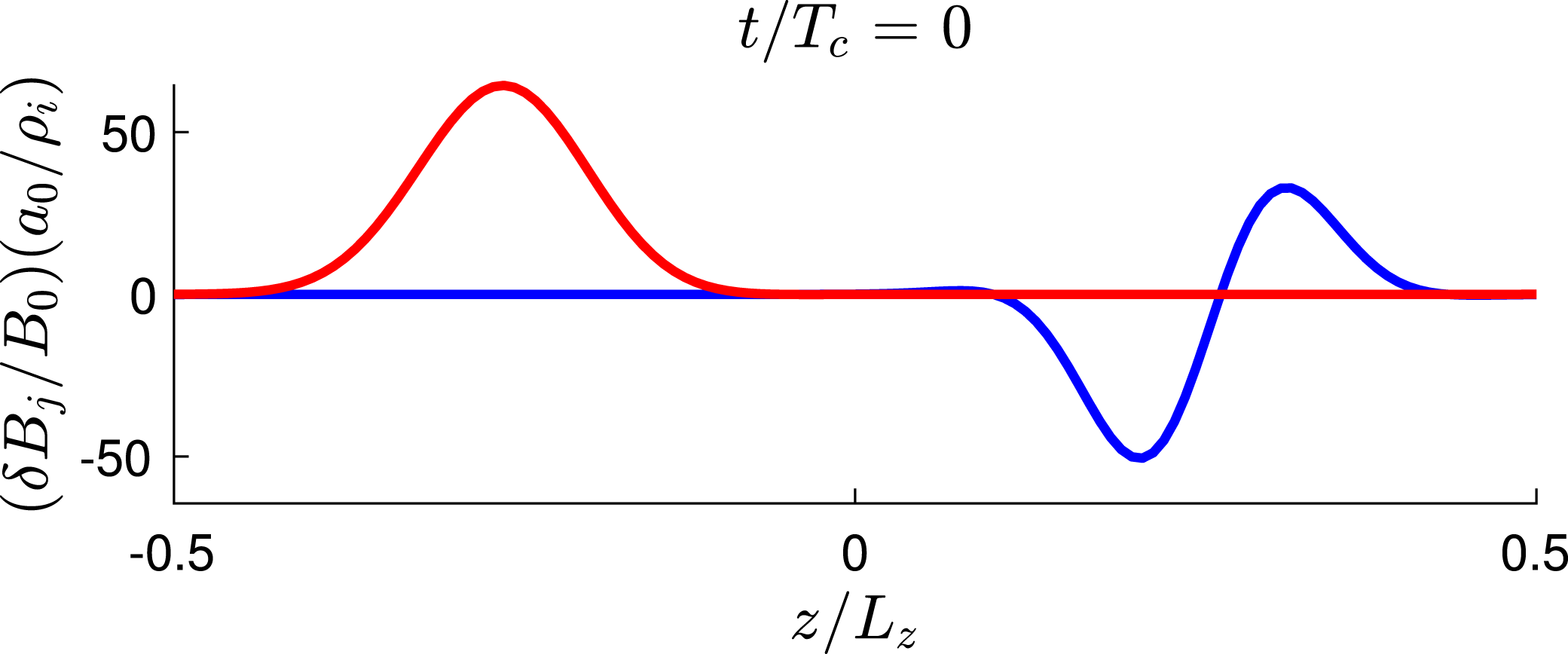
Figure 1. Schematic of the initial conditions specifying the two perpendicularly polarized, counterpropagating Alfvén wavepackets localized within the periodic domain. Plotted is the
$z$
-dependence of the normalized amplitudes of the perpendicular magnetic field perturbation
$(\unicode[STIX]{x1D6FF}B_{y}/B_{0})(a_{0}/\unicode[STIX]{x1D70C}_{0})$
for the unipolar wavepacket (red) and of the perpendicular magnetic field perturbation
$(\unicode[STIX]{x1D6FF}B_{x}/B_{0})(a_{0}/\unicode[STIX]{x1D70C}_{0})$
for the dipolar wavepacket (blue). The unipolar wavepacket has a perpendicular wavevector
$\boldsymbol{k}_{\bot }^{-}=(k_{x}L_{\bot },k_{y}L_{\bot })=(1,0)$
and the dipolar wavepacket has
$\boldsymbol{k}_{\bot }^{+}=(0,1)$
.
The functional forms along
$z$
of the initial Alfvén wavepackets used in this simulation are shown in figure 1. Initially at
$z<0$
is a wavepacket with a magnetic field perturbation
$\unicode[STIX]{x1D6FF}B_{y}$
polarized in the
$y$
direction, a unipolar variation in
$z$
(red) and a perpendicular structure with wavenumber
$\boldsymbol{k}_{\bot }^{-}=(k_{x}L_{\bot },k_{y}L_{\bot })=(1,0)$
. The eigenfunction dictating the different field components and perturbed distribution functions for this Alfvén wavepacket is determined by solving the linear, collisionless, gyrokinetic dispersion relation (Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) for an Alfvén mode with the chosen perpendicular Fourier wavevector
$(k_{x},k_{y})$
to obtain the complex eigenfrequency
$\unicode[STIX]{x1D714}$
, the complex Fourier coefficients for the eigenfunctions of the electromagnetic potentials
$\hat{\unicode[STIX]{x1D719}}$
,
$\hat{A}_{\Vert }$
and
$\unicode[STIX]{x1D6FF}\hat{B}_{\Vert }$
, and the complex perturbed gyrokinetic distribution functions for the ions
${\hat{h}}_{i}(v_{\Vert },v_{\bot })$
and electrons
${\hat{h}}_{e}(v_{\Vert },v_{\bot })$
, where the hat symbol denotes the
$(k_{x},k_{y})$
Fourier coefficient (Nielson et al.
Reference Nielson, Howes and Dorland2013). The procedure for localizing this Alfvén wavepacket in the
$z$
direction is described in appendix A. Through this procedure, the unipolar Alfvén wavepacket in figure 1 propagates in the
$+z$
direction. The other Alfvén wavepacket, initially at
$z>0$
, has a magnetic field perturbation
$\unicode[STIX]{x1D6FF}B_{x}$
polarized in the
$x$
direction, a dipolar structure in
$z$
(blue) and a perpendicular structure with wavenumber
$\boldsymbol{k}_{\bot }^{+}=(k_{x}L_{\bot },k_{y}L_{\bot })=(0,1)$
; the eigenfunction specified by the same procedure dictates that this dipolar wavepacket propagates in the
$-z$
direction. Note that these unsymmetric initial conditions were chosen to further test the complexities in Alfvén wave collisions. In particular by having a unipolar wavepacket, the collision does not shear and unshear in an oscillatory manner as it does in the interaction between two dipolar wavepackets.
The plasma parameters for this strong Alfvén wavepacket collision simulation are ion plasma beta
$\unicode[STIX]{x1D6FD}_{i}=1$
and ion-to-electron temperature ratio
$T_{i}/T_{e}=1$
. To study the nonlinear evolution of this Alfvén wavepacket collision in the limit
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
, we choose a perpendicular simulation domain size
$L_{\bot }=40\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{i}$
with simulation resolution
$(n_{x},n_{y},n_{z},n_{\unicode[STIX]{x1D706}},n_{\unicode[STIX]{x1D700}},n_{s})=(64,64,128,32,32,2)$
. Therefore, the initial Alfvén wavepackets have perpendicular wavevectors
$\boldsymbol{k}_{\bot }^{-}=(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i})=(0.05,0)$
for the unipolar wavepacket and
$\boldsymbol{k}_{\bot }^{+}=(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i})=(0,0.05)$
for the dipolar wavepacket, so both waves have the same initial perpendicular wavenumber
$k_{\bot }^{\pm }\unicode[STIX]{x1D70C}_{i}=0.05$
, but are polarized perpendicular to each other. The fully resolved perpendicular range in this dealiased pseudospectral method covers
$0.05\leqslant k_{\bot }\unicode[STIX]{x1D70C}_{i}\leqslant 1.05$
. Here the ion thermal Larmor radius is
$\unicode[STIX]{x1D70C}_{i}=v_{ti}/\unicode[STIX]{x1D6FA}_{i}$
, the ion thermal velocity is
$v_{ti}^{2}=2T_{i}/m_{i}$
, the ion cyclotron frequency is
$\unicode[STIX]{x1D6FA}_{i}=q_{i}B_{0}/(m_{i}c)$
and the temperature is given in energy units. The parallel length of the simulation domain is
$L_{z}$
, extending over the range [
$-L_{z}/2,L_{z}/2$
]. Note that the simulation domain is triply periodic, so when a wavepacket exits the domain at
$z=\pm L_{z}/2$
, it reenters at the opposite end at
$z=\mp L_{z}/2$
, enabling these two wavepackets to undergo successive collisions with each other. The linearized Landau collision operator (Abel et al.
Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al.
Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) is employed with collisional coefficients
$\unicode[STIX]{x1D708}_{i}=\unicode[STIX]{x1D708}_{e}=10^{-3}$
, yielding weakly collisional dynamics with
$\unicode[STIX]{x1D708}_{s}/\unicode[STIX]{x1D714}\ll 1$
.
The amplitude of the initial wavepackets is parameterized by the nonlinearity parameter (Goldreich & Sridhar Reference Goldreich and Sridhar1995), defined by taking the ratio of the magnitudes of the linear to the nonlinear terms in the incompressible MHD equations (Howes & Nielson Reference Howes and Nielson2013; Nielson et al.
Reference Nielson, Howes and Dorland2013). In terms of Elsasser variables, defined by
$\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \unicode[STIX]{x1D6FF}\boldsymbol{B}/\sqrt{4\unicode[STIX]{x03C0}(n_{0i}m_{i}+n_{0e}m_{e})}$
, the nonlinearity parameter is defined by
$\unicode[STIX]{x1D712}^{\pm }\equiv |\boldsymbol{z}^{\mp }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }|/|\boldsymbol{v}_{A}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }|$
, where
$\unicode[STIX]{x1D712}^{\pm }$
characterizes the strength of the nonlinear distortion of the
$\boldsymbol{z}^{\pm }$
Alfvén wave by the counterpropagating
$\boldsymbol{z}^{\mp }$
Alfvén wave. For the particular initial Alfvén wavepackets shown in figure 1, the nonlinearity parameter simplifies to
$\unicode[STIX]{x1D712}^{\pm }=2k_{\bot }\unicode[STIX]{x1D6FF}B_{\bot }^{\mp }/(k_{\Vert }B_{0})$
. With the
$\boldsymbol{z}^{\pm }$
wavepackets having parallel wavenumbers of approximately
$k_{\Vert }a_{0}=\mp 3$
, where
$a_{0}=L_{z}/2\unicode[STIX]{x03C0}$
, the amplitude of the unipolar wavepacket
$(\unicode[STIX]{x1D6FF}B_{\bot }^{-}/B_{0})(a_{0}/\unicode[STIX]{x1D70C}_{i})\simeq 60$
gives
$\unicode[STIX]{x1D712}^{+}=2$
and the amplitude of the dipolar wavepacket
$(\unicode[STIX]{x1D6FF}B_{\bot }^{+}/B_{0})(a_{0}/\unicode[STIX]{x1D70C}_{i})\simeq 40$
gives
$\unicode[STIX]{x1D712}^{-}=1.3$
. Strong, critical balanced turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995) corresponds to a nonlinearity parameter of
$\unicode[STIX]{x1D712}\sim 1$
, so this simulation falls into the desired limit of strong Alfvén wavepacket collisions.
3 Evolution of the nonlinear interaction
Figure 2. Three-dimensional isocontours of the normalized parallel current density
$j_{z}/j_{0}$
between Alfvén wavepacket collisions at (a)
$t/T_{c}=0$
, (c)
$t/T_{c}=1$
and (e)
$t/T_{c}=2$
and at the midpoint of collisions at (b)
$t/T_{c}=0.5$
, (d)
$t/T_{c}=1.5$
and ( f)
$t/T_{c}=2.5$
.
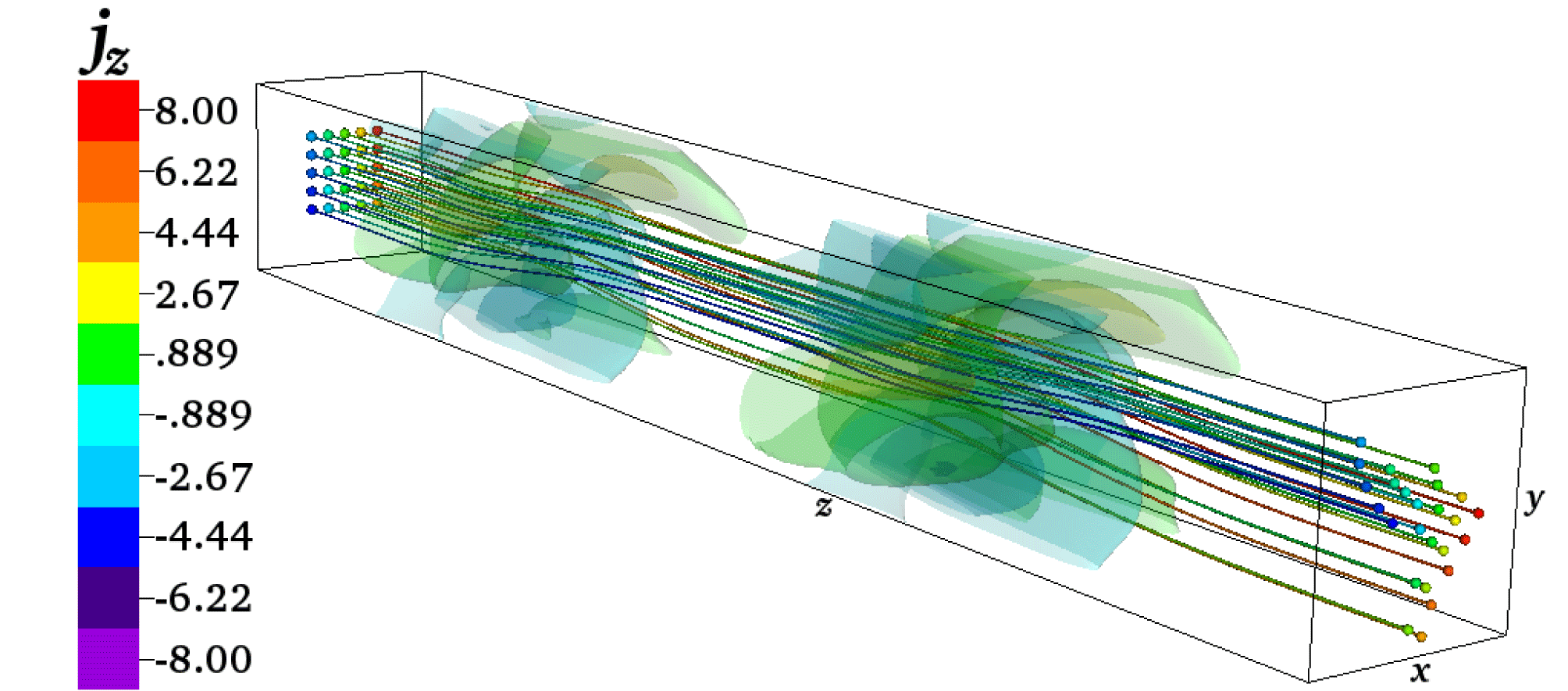
Figure 3. Three-dimensional movie (see supplementary movie https://doi.org/10.1017/S0022377817001003) of perpendicularly polarized counterpropagating localized Alfvén wavepacket collisions. The rainbow lines that extend along the length of the box represent magnetic field lines and the rainbow contours represent isocontours of the current in the
$z$
-direction,
$J_{z}$
.
The basic evolution of this strong Alfvén wavepacket collision simulation is illustrated by three-dimensional contour plots of the parallel current density
$j_{z}$
associated with each of the interacting wavepackets, shown in figure 2 and displayed as a movie in figure 3. Time is normalized in terms of the time for a single Alfvén wavepacket collision,
$T_{c}$
, during which the initially separated Alfvén wavepackets approach each other along
$z$
(with the
$+z$
direction from left to right in figure 2), overlap and interact nonlinearly, and then move away from each other after the collision. At
$t=0$
, the unipolar wavepacket is centred at
$z=-L_{z}/4$
, and the dipolar wavepacket at
$z=+L_{z}/4$
; during a collision time
$T_{c}$
, each wavepacket propagates at the Alfvén velocity
$v_{A}$
over a parallel distance
$L_{z}/2$
. The midpoint of each collision occurs at
$t/T_{c}=0.5,1.5,2.5$
.
In figure 2(a) are plotted isocontours of the normalized parallel current density
$j_{z}/j_{0}$
for each of the wavepackets at
$t=0$
, where the current density is normalized by
$j_{0}=n_{0}q_{i}v_{ti}L_{\bot }/L_{z}$
. It is clear that the unipolar wavepacket (at
$z<0$
, left side) initially has only perpendicular variation in the
$x$
direction, while the dipolar wavepacket (at
$z>0$
, right side) initially has only perpendicular variation in the
$y$
direction. Figure 2(b) shows the midpoint of the first collision occurring at
$z=0$
and
$t/T_{c}=0.5$
, showing a significantly more complicated perpendicular structure parallel current density
$j_{z}$
.
After the first collision at
$t/T_{c}=1.0$
in figure 2(c), the unipolar wavepacket, now at
$z=+L_{z}/4$
, has gained some variation in the
$y$
direction, and the dipolar wavepacket, now at
$z=-L_{z}/4$
, has developed variation in the
$x$
direction. Each wavepacket has been distorted by passing through, and interacting nonlinearly with, the counterpropagating wavepacket. Mathematically, when expressed in terms of Fourier modes, the strong Alfvén wavepacket collision has mediated the nonlinear transfer of energy from the two initial perpendicular Fourier modes to other Fourier modes with larger values of
$k_{\bot }$
, as shown quantitatively in § 3.1. Therefore this visualization clearly shows the nonlinear cascade of energy to smaller scales in strong Alfvén wavepacket collisions, the fundamental building block of astrophysical plasma turbulence, a key result of this study.
Because the simulation domain is periodic in the
$z$
direction, the Alfvén wavepackets undergo a second collision at the boundary of the domain
$z=\pm L_{z}/2$
at
$t/T_{c}=1.5$
, shown in figure 2(d), followed by a third collision at
$z=0$
at
$t/T_{c}=2.5$
, shown in figure 2( f). Below we explore in more detail the cascade of energy to smaller perpendicular scales, the development of current sheets, the evolution of the energy in perpendicular Fourier modes and key properties of localized Alfvén wavepacket collisions.
3.1 The perpendicular cascade of energy
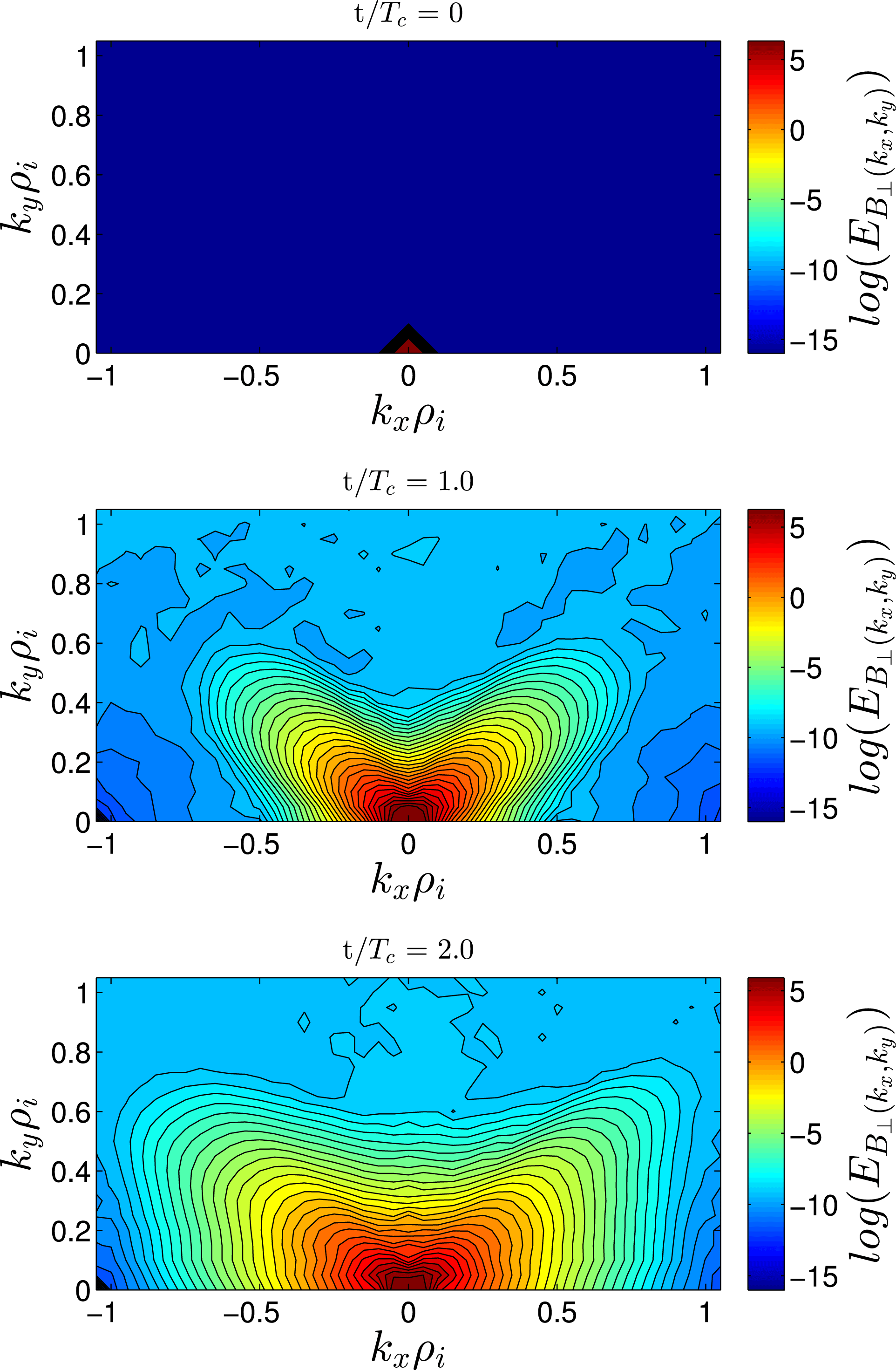
Figure 4. Plots of the perpendicular magnetic energy
$E_{B_{\bot }(k_{x},k_{y})}$
(arbitrary units) on a log scale in the perpendicular Fourier plane
$(k_{x},k_{y})$
(a) at the initial time
$t/T_{c}=0$
, (b) after the first strong Alfvén wavepacket collision at
$t/T_{c}=1$
and (c) after the second strong Alfvén wavepacket collision at
$t/T_{c}=2$
.
To explore the nonlinear cascade of smaller perpendicular scales in this strong Alfvén wavepacket collision simulation, we plot in figure 4 the perpendicular magnetic energy of fluctuations in perpendicular Fourier space integrated over
$z$
,
$E_{B_{\bot }(k_{x},k_{y})}\equiv \int _{-L_{z}/2}^{L_{z}/2}\,\text{d}z|\unicode[STIX]{x1D6FF}B_{\bot }(k_{x},k_{y})|^{2}/8\unicode[STIX]{x03C0}$
in arbitrary units. In figure 4(a) is the perpendicular magnetic energy of the initial Alfvén wavepackets at
$t=0$
, showing all of the energy is contained within the three perpendicular Fourier modes
$(k_{x}\unicode[STIX]{x1D70C}_{i},k_{y}\unicode[STIX]{x1D70C}_{i})=(1,0)$
,
$(0,1)$
and
$(-1,0)$
. Note that AstroGK uses a reality condition imposed on the complex Fourier coefficients such that the magnetic field can be described using only Fourier modes in the upper half-plane
$k_{y}\geqslant 0$
. The reality condition requires
$\unicode[STIX]{x1D6FF}\hat{B}(k_{x},k_{y})=\unicode[STIX]{x1D6FF}\hat{B}^{\ast }(-k_{x},-k_{y})$
, so if there is power in the
$(1,0)$
mode, there must be equivalent power in the
$(-1,0)$
mode, as seen in figure 4(a).
After the first collision at
$t/T_{c}=1$
, figure 4(b) shows clearly that the strong nonlinear interactions have transferred significant energy to many other modes in the perpendicular Fourier plane
$(k_{x},k_{y})$
. Note that the perpendicular wavenumber is given by
$k_{\bot }=\sqrt{k_{x}^{2}+k_{y}^{2}}$
, so that modes further away from the origin represent smaller scale fluctuations in the perpendicular plane. The plot after the second collision at
$t/T_{c}=2$
in figure 4(c) shows that successive collisions continue to facilitate the perpendicular cascade of energy. These results demonstrate that the finding from the idealized periodic case – that Alfvén wave collisions mediate the nonlinear transfer of energy to smaller perpendicular scales – indeed persists in the more realistic case of localized Alfvén wavepacket collisions, answering the first key question posed in the introduction.
3.2 Current sheet development
Figure 5. Plot of the normalized parallel current density
$j_{z}/j_{0}$
at
$z=0$
during the first collision at (a)
$t/T_{c}=0.3$
and (b)
$t/T_{c}=0.5$
, at
$z=L_{z}/2$
during second collision at (c)
$t/T_{c}=1.3$
and (d)
$t/T_{c}=1.5$
and at
$z=0$
during the third collision at (a)
$t/T_{c}=2.3$
and (b)
$t/T_{c}=2.5$
.
For plane Alfvén wave collisions in the idealized periodic case, plots of the parallel current density
$j_{z}$
in the
$(x,y)$
plane perpendicular to the equilibrium magnetic field demonstrate that strong Alfvén wave collisions self-consistently generate current sheets (Howes Reference Howes2016). These current sheets extended the full parallel length of the original Alfvén waves, with widths in the perpendicular plane of approximately the perpendicular wavelength of the original interacting Alfvén waves, but with a much smaller thickness in the perpendicular plane. Here we use plots of the
$(x,y)$
plane perpendicular to the equilibrium magnetic field to determine whether this current sheet formation persists in the more realistic case of strong collisions between localized Alfvén wavepackets.
Figure 6. Plot of the normalized parallel current density
$j_{z}/j_{0}$
of colliding Alfvén wavepackets before the first collision at
$t=0$
for (a) the unipolar wave at
$z=-L_{z}/4$
and (b) the dipolar wave at
$z=+L_{z}/4$
, after the first collision when the wavepackets have separated for (c) the unipolar wave at
$z=+L_{z}/4$
and
$t/T_{c}=0.98$
and (d) the dipolar wave at
$z=-L_{z}/4$
and
$t/T_{c}=0.96$
and after the second collision for (e) the unipolar wave at
$z=-L_{z}/4$
and
$t/T_{c}=2.1$
and ( f) the dipolar wave at
$z=+L_{z}/4$
and
$t/T_{c}=2.0$
.
First, we examine the development of the parallel current density
$j_{z}$
in the
$(x,y)$
plane during the course of each collision. In figure 5, we plot the normalized parallel current density
$j_{z}/j_{0}$
at
$z=0$
(a) early in the first collision at
$t/T_{c}=0.3$
and (b) later in the same collision at
$t/T_{c}=0.5$
, where we remind the reader that the midpoint of each collision occurs at
$t/T_{c}=0.5,1.5,2.5$
. The nearly circular
$j_{z}$
pattern in figure 5(a) is largely due to the linear superposition of the current of each of the initial Alfvén wavepackets (the top row of figure 6 shows the current patterns of each of the initial Alfvén wavepackets). The nonlinear interaction of the Alfvén wavepackets during the first collision leads to the thinning of these initial circular current patterns into a more sheet-like morphology in figure 5(b). Figure 5(c,d) shows the evolution of the second collision in the plane
$z=L_{z}/2$
(at the parallel boundary of the periodic domain) at (c)
$t/T_{c}=1.3$
and (d)
$t/T_{c}=1.5$
. Here we see the current sheets becoming yet more elongated and intense through the course of the second collision. Figure 5(e,f) shows plots of
$j_{z}/j_{0}$
during the third collision at
$z=0$
, with further thinning and intensification of the current sheets. Note that the three-dimensional isocontours of
$j_{z}$
in figure 2 show that the parallel extent of the current sheets is the same as the parallel length of the original wavepackets.
These results show clearly that strong collisions of localized Alfvén wavepackets indeed self-consistently generate intermittent current sheets, answering the second question in the introduction.
Another important question, however, is whether the current sheets that develop during the wavepacket collisions persist within each wavepacket after the collision. In figure 6, we show the initial pattern at
$t=0$
of the normalized parallel current density
$j_{z}/j_{0}$
for (a) the unipolar wave at
$z=-L_{z}/4$
with only variation in the
$x$
direction and (b) the dipolar wave at
$z=+L_{z}/4$
with only variation in the
$y$
direction. After the first collision, we show
$j_{z}$
for (c) the unipolar wave at
$z=+L_{z}/4$
and
$t/T_{c}=0.98$
and (d) the dipolar wave at
$z=-L_{z}/4$
and
$t/T_{c}=0.96$
. At this time when the wavepackets are no longer overlapping in
$z$
, one can clearly see the distortion of current density pattern, due to the previous collision, has led to a thinning and intensification of the current density into a more sheet-like morphology that persists after the wavepackets have separated. After the second collision, we plot (e) the unipolar wave at
$z=-L_{z}/4$
and
$t/T_{c}=2.1$
and ( f) the dipolar wave at
$z=+L_{z}/4$
and
$t/T_{c}=2.0$
. Here we can see that the current sheets that develop as a consequence of the strong Alfvén wavepacket collisions indeed persist within the wavepackets after the collision is over, showing that these interactions in the more realistic case may explain the ubiquitous observations of intermittent current sheets in plasma turbulence.
3.3 Evolution of energy
A simple physical interpretation of the evolution of the energy in this localized Alfvén wavepacket collision can be developed using the equations of incompressible MHD for guidance. These equations, written in terms of Elsasser variables, take the form
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{z}^{\pm }}{\unicode[STIX]{x2202}t}\mp \boldsymbol{v}_{A}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }=-\boldsymbol{z}^{\mp }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }-\unicode[STIX]{x1D735}P/(n_{0i}m_{i}+n_{0e}m_{e}),\end{eqnarray}$$
and
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{z}^{\pm }=0$
. Here
$\boldsymbol{v}_{A}=\boldsymbol{B}_{0}/\sqrt{4\unicode[STIX]{x03C0}(n_{0i}m_{i}+n_{0e}m_{e})}$
is the Alfvén velocity due to the equilibrium field
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
where
$\boldsymbol{B}=\boldsymbol{B}_{0}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
,
$P$
is total pressure (thermal plus magnetic) and
$n_{0i}m_{i}+n_{0e}m_{e}$
is mass density. Recall that the Elsasser variables are defined by
$\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \unicode[STIX]{x1D6FF}\boldsymbol{B}/\sqrt{4\unicode[STIX]{x03C0}(n_{0i}m_{i}+n_{0e}m_{e})}$
, representing waves that propagate up or down the mean magnetic field. The nonlinear term,
$\boldsymbol{z}^{\mp }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }$
, governs the nonlinear interactions of the counterpropagating Alfvén wave collisions.
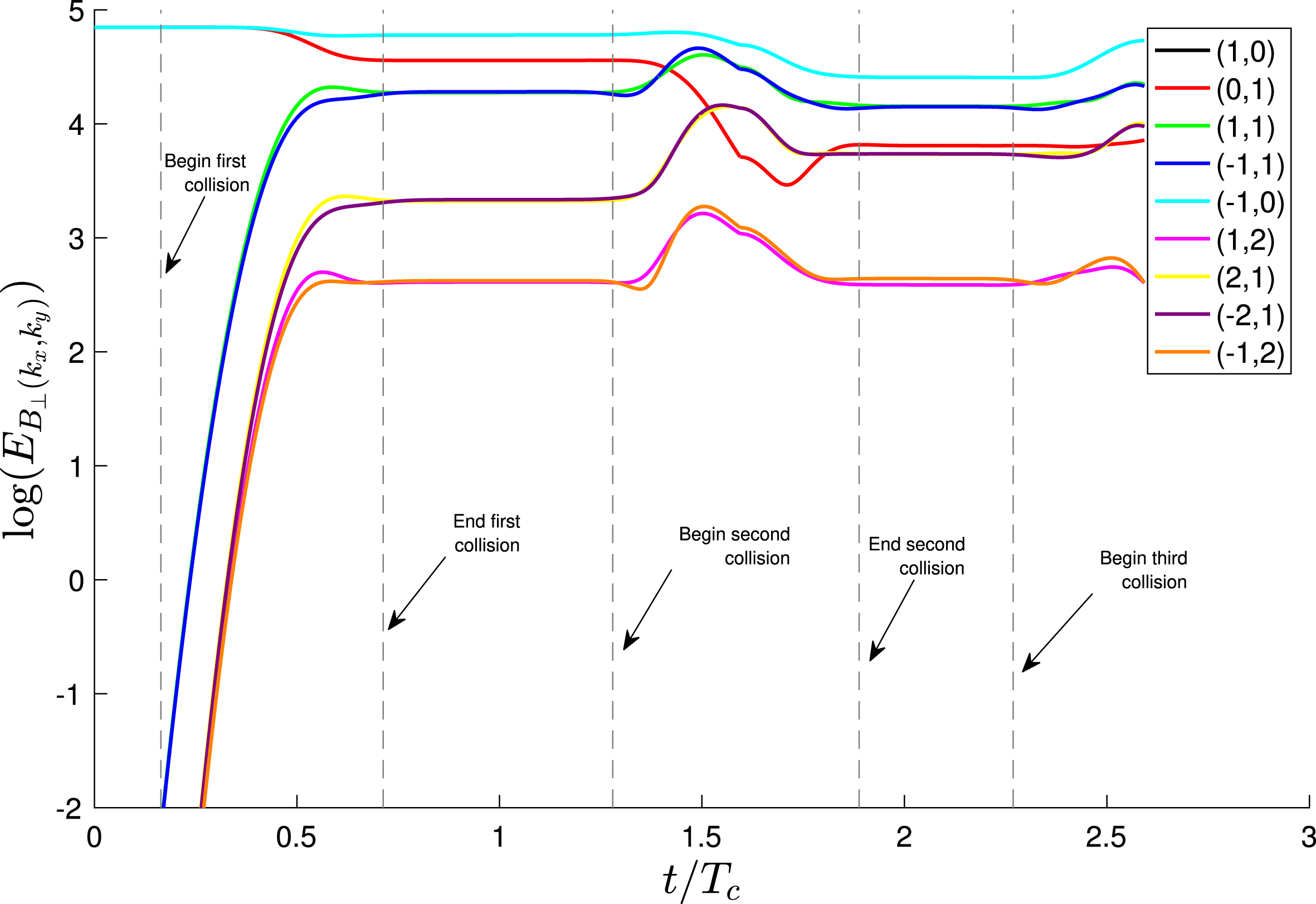
Figure 7. Plot of the evolution of energy transfer between
$(k_{x},k_{y})$
modes. Note that the
$(1,0)$
mode is plotted as the same line as the cyan
$(-1,0)$
mode, indicating they are identical.
In figure 7, we plot the temporal evolution of the magnetic energy
$E_{B_{\bot }(k_{x},k_{y})}$
in some of the lowest perpendicular Fourier modes
$(k_{x},k_{y})$
, illustrating some of the key properties of Alfvén wavepacket collisions. The first main point is that there is no nonlinear transfer of energy among Fourier modes until the two wavepackets begin to overlap in space along
$z$
(first vertical dashed line). As expected from theoretical considerations of incompressible MHD turbulence (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965; Sridhar & Goldreich Reference Sridhar and Goldreich1994; Montgomery & Matthaeus Reference Montgomery and Matthaeus1995; Ng & Bhattacharjee Reference Ng and Bhattacharjee1996; Galtier et al.
Reference Galtier, Nazarenko, Newell and Pouquet2000; Howes & Nielson Reference Howes and Nielson2013), the nonlinear interaction is zero unless both
$z^{-}$
(the unipolar wavepacket) and
$z^{+}$
(the dipolar wavepacket) are both non-zero at the same point in space, as can be seen by inspection of the nonlinear term
$\boldsymbol{z}^{\mp }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{z}^{\pm }$
. Between collisions, when the wavepackets have no overlap in
$z$
, there is no nonlinear transfer of energy among different
$(k_{x},k_{y})$
modes, as clearly seen in figure 7. The second main point is that the perpendicular Fourier modes
$(k_{x}L_{\bot },k_{y}L_{\bot })$
of the initial Alfvén wavepackets,
$(1,0)$
and
$(0,1)$
generally lose energy to nonlinearly generated perpendicular Fourier modes during each collision. This is the transfer of energy to smaller perpendicular scales, illustrated by the plots of perpendicular magnetic energy in
$(k_{x},k_{y})$
Fourier space in figure 4. A more quantitative examination contrasting the nonlinear transfer of energy between the idealized plane Alfvén wave collisions in a periodic geometry and localized Alfvén wavepackets collisions, in both the weakly and strongly nonlinear limits, will be presented in a subsequent paper (Verniero & Howes Reference Verniero and Howes2018).
3.4 Wavepacket collisions
The three-dimensional visualization of this localized Alfvén wavepacket collision in figure 2 presents a concise overview of many of the properties examined above. The series of panels (a) through (c) show clearly the distortion of the original wavepackets that arises during the collision and persists after the wavepackets have separated again. This is a physical visualization of the nonlinear cascade of energy to smaller scales, the key characteristic of turbulence in space and astrophysical plasmas. Although a little difficult to see clearly in the three-dimensional projection in figure 2, the nonlinear evolution of this strong Alfvén wavepacket collision also leads to the self-consistent generation of a sheet-like morphology for the regions of intense parallel current density
$j_{z}$
. This thinning and intensifying of the current into sheets is more clearly seen in the perpendicular cross-section at
$z=L_{z}/2$
(the right-hand
$z$
boundary of the simulation domain) in figure 2(d); the same cross-section at
$z=L_{z}/2$
is also shown in figure 5(d).
In addition to the isocontours of the normalized parallel current density
$j_{z}/j_{0}$
, we also plot the paths of a sample of magnetic field lines as they traverse the domain. Beginning at points on a
$5\times 5$
grid at
$z=-L_{z}/2$
, we trace the field lines in the
$+z$
direction. Although the perpendicular magnetic field fluctuation associated with each Alfvén wavepacket is small compared to the equilibrium magnetic field,
$\unicode[STIX]{x1D6FF}B_{\bot }\ll B_{0}$
, one can still see the distortion of the field lines as they pass through each wavepacket. In the space between wavepackets, both before and after each collision, the magnetic field lines are straight and uniform, further illustrating the point that nonlinear evolution ceases when the wavepackets are separated, even in a gyrokinetic simulation where dispersive and kinetic effects are resolved.
It is worthwhile also noting the important point that, even after each strong Alfvén wavepacket collision, the individual wavepackets continue to propagate along the equilibrium magnetic field and they remain localized in
$z$
. There is a very small spreading of the wavepacket, hardly noticeable in figure 2, due to the fact that Alfvén waves become dispersive at
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$
, with an increasing parallel group velocity. Therefore, some of the higher
$k_{\bot }$
modes that are nonlinearly generated by the strong Alfvén wavepacket collision in this gyrokinetic simulation – a numerical approach that resolves these dispersive kinetic effects at
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$
– will propagate a little faster than Alfvén waves in the MHD limit
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
that have a parallel group velocity at the Alfvén speed
$v_{g\Vert }=v_{A}$
, causing a slight spreading out of the localized wavepacket.
3.5 Relation to similar wavepacket collision simulations
A recent study by Pezzi et al. (Reference Pezzi, Parashar, Servidio, Valentini, Vásconez, Yang, Malara, Matthaeus and Veltri2017) has used numerical simulations to tackle what they term the ‘Parker–Moffatt problem.’ The basic question is inspired by the properties of incompressible MHD equations given in § 3.1: do two initially separated, localized Alfvén wavepackets interact nonlinearly only during the time that they overlap, and then cease evolving after they have passed through each other and become separated again? The simulation results shown in figure 2, and examined in further detail in the subsections above, definitively answer this question – yes.
The results of the gyrokinetic simulation of strong Alfvén wavepacket collisions presented here, however, stand in stark contrast to the results of the study by Pezzi et al. (Reference Pezzi, Parashar, Servidio, Valentini, Vásconez, Yang, Malara, Matthaeus and Veltri2017), which find that after the collision, in both their compressible MHD and Hybrid Vlasov–Maxwell simulations, the wavepackets do not separate cleanly and continue to evolve, as illustrated in figure 1 of their paper. What is the cause for the dramatic contradiction in these results?
We argue here that the limitation of the Pezzi et al. (Reference Pezzi, Parashar, Servidio, Valentini, Vásconez, Yang, Malara, Matthaeus and Veltri2017) simulations to two spatial dimensions is the root of these striking differences. Due to the large computational cost of running the Hybrid Vlasov–Maxwell (HVM) code (Valentini et al.
Reference Valentini, Trávníček, Califano, Hellinger and Mangeney2007) in three spatial dimensions, the authors chose to approximate the three-dimensional problem by using an oblique two-dimensional approach (Howes Reference Howes2014), where spatial variation is allowed in two dimensions in the
$(x,y)$
plane, but the equilibrium magnetic field is slightly tilted away from the normal to the plane,
$\boldsymbol{B}_{0}=B_{0}(\sin \unicode[STIX]{x1D703}\hat{\boldsymbol{x}}+\cos \unicode[STIX]{x1D703}\hat{\boldsymbol{z}})$
with
$\unicode[STIX]{x1D703}=6^{\circ }$
, yielding a small component of the equilibrium magnetic field in the
$x$
direction. Since plane Alfvén waves only propagate if there is a non-zero component of the wavevector parallel to the equilibrium magnetic field,
$k_{\Vert }\neq 0$
, this trick enables the
$x$
component of a wavevector to have a small component parallel to
$\boldsymbol{B}_{0}$
, enabling propagating Alfvén waves to be simulated.
The limitation to two spatial dimensions has two important effects: (i) it precludes the possibility of initializing two perpendicularly polarized, counterpropagating wavepackets (as initialized here), which is the essential set-up of the Parker–Moffatt problem to be studied; and (ii) it significantly limits the nonlinear couplings that can arise, constraining the results in an unphysical way (Howes Reference Howes2014).
Although Pezzi et al. (Reference Pezzi, Parashar, Servidio, Valentini, Vásconez, Yang, Malara, Matthaeus and Veltri2017) state that they set up two Alfvénic wavepackets, several pieces of evidence suggest that their initial wavepackets are indeed not Alfvénic. First, they initialize the fluctuations by imposing the constraint that fluctuations are strictly transverse to the equilibrium magnetic field
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}=0$
. Although this is a necessary condition for an Alfvén wave, it is not sufficient: the polarization of the magnetic field fluctuation for the Alfvén wave with wavevector
$\boldsymbol{k}$
must also be oriented in the direction given by
$\boldsymbol{B}_{0}\times \boldsymbol{k}$
(Maron & Goldreich Reference Maron and Goldreich2001; Howes & Nielson Reference Howes and Nielson2013; Howes Reference Howes2014). Any component of the magnetic field fluctuation in the other direction of the plane given by
$\boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}=0$
represents not an Alfvén wave, but a different mode: in incompressible MHD, it would belong to the pseudo-Alfvén wave (Maron & Goldreich Reference Maron and Goldreich2001; Howes & Nielson Reference Howes and Nielson2013; Howes Reference Howes2014), and in compressible MHD, it would represent some combination of the fast and slow magnetosonic modes (Cho & Lazarian Reference Cho and Lazarian2003). That their initialization in fact excites some magnetosonic modes is supported by two results in their paper. First, their initialization excites density fluctuations even before the wavepackets collide, a feature they attribute to magnetic pressure fluctuations due to finite-amplitude magnetic fluctuations, but that could simply be because their initialization directly included these linear magnetosonic modes. Second, even before the waves collide in the MHD simulation, shown in the upper left panel of their figure 1, one can see small disturbances well ahead of and behind each wavepacket, suggesting that magnetosonic modes, which have a different group velocity from the Alfvén mode, are dispersively spreading out the wavepacket, a linear effect.
The second impact of the limitation to two spatial dimensions is that the nonlinear couplings possible in the oblique two-dimensional configuration are unphysically constrained relative to the three-dimensional case, as explained in detail in Howes (Reference Howes2014). This constraint can artificially enhance the nonlinear coupling to magnetosonic modes relative to the coupling to Alfvénic modes, dramatically altering the nonlinear evolution.
Our perspective is that any investigation of the so-called Parker–Moffatt problem is most cleanly performed in three spatial dimensions. Our results show definitively that when two localized Alfvén wavepackets collide, the interaction occurs only while they overlap, ceasing when the wavepackets separate cleanly, leaving distorted wavepackets that have essentially the same finite extent along the equilibrium magnetic field. Before concluding, it is also worthwhile emphasizing that our results were obtained with a gyrokinetic simulation that resolves all of the low-frequency – not including cyclotron and fast magnetosonic physics (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) – compressible and kinetic effects of a weakly collisional plasma.
4 Conclusion
Our results here show that many of the fundamental properties of Alfvén wave collisions, originally characterized analytically and numerically in the idealized case of a periodic Alfvén wave collision, persist under the more realistic conditions of a localized Alfvén wavepacket collision. Specifically, we have demonstrated that strong localized Alfvén wavepacket collisions are effective in mediating the nonlinear cascade of energy to small perpendicular scales, as demonstrated in figure 4. Furthermore, we have shown that strong localized Alfvén wavepacket collisions also self-consistently generate current sheets that persist even between collisions, as shown in figures 5 and 6, confirming a robust mechanism to explain the ubiquitous current sheets observed in numerical simulations of plasma turbulence (Wan et al. Reference Wan, Matthaeus, Karimabadi, Roytershteyn, Shay, Wu, Daughton, Loring and Chapman2012; Karimabadi et al. Reference Karimabadi, Roytershteyn, Wan, Matthaeus, Daughton, Wu, Shay, Loring, Borovsky and Leonardis2013; TenBarge & Howes Reference TenBarge and Howes2013; Wu et al. Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Zhdankin et al. Reference Zhdankin, Uzdensky, Perez and Boldyrev2013) and inferred from measurements of solar wind turbulence (Borovsky & Denton Reference Borovsky and Denton2011; Osman et al. Reference Osman, Matthaeus, Greco and Servidio2011, Reference Osman, Matthaeus, Wan and Rappazzo2012; Perri et al. Reference Perri, Goldstein, Dorelli and Sahraoui2012; Wang et al. Reference Wang, Tu, He, Marsch and Wang2013; Wu et al. Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Osman et al. Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan2014).
The overall evolution of localized Alfvén wavepacket collisions involves strong nonlinear interactions occurring while the wavepackets overlap, followed by a clean separation of the wavepackets with straight uniform magnetic fields in between and the cessation of nonlinear evolution, as visualized in figure 2. The wavepackets remain localized along the equilibrium magnetic field before and after each wavepacket collision. It is important to emphasize that these characteristics are predicted based on the properties of the incompressible MHD equations, but are found even in the gyrokinetic simulation presented here which resolves dispersive and kinetic effects beyond the reach of the MHD theory. That these important properties of Alfvén wave collisions persist in the realistic localized wavepacket case further supports the contention that Alfvén wave collisions represent the fundamental building block of astrophysical plasma turbulence.
Previous analytical and numerical work in the limit of weakly nonlinear, periodic Alfvén wave collisions, (Howes & Nielson Reference Howes and Nielson2013; Nielson et al. Reference Nielson, Howes and Dorland2013) has shown that a nonlinearly generated mode, which is not a solution of the linear dispersion relation, serves to mediate the energy transfer to small perpendicular scales. Future work will address the question of whether this nonlinearly generated mode still plays a key role in the more realistic case of localized Alfvén wavepacket collisions (Verniero & Howes Reference Verniero and Howes2018).
Acknowledgements
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under grant no. 1048957, NSF PHY-10033446, NSF CAREER AGS-1054061, and DOE DE-SC0014599. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725. We especially thank D. Pugmire (OLCF) and T. Jenkins (Tech-X). This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant no. ACI-1053575, through NSF XSEDE Award PHY090084.
Appendix A. Windowing function for localized Alfvén wavepacket collisions
A.1 Parallel dependence of Alfvén eigenfunctions
Initializing Alfvén wavepackets localized along the equilibrium magnetic field using the AstroGK code (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010) takes advantage of the remarkable feature of gyrokinetics that the linear collisionless gyrokinetic dispersion relation, when suitably normalized, is independent of the parallel wavenumber of fluctuations, as explained below.
For a fully ionized proton–electron plasma with Maxwellian equilibrium velocity distributions and zero net drift velocities, the complex frequency that is the solution of the Vlasov–Maxwell linear dispersion relation (Stix Reference Stix1992; Quataert Reference Quataert1998) can be expressed as a function of five dimensionless parameters,
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{i}=\tilde{\unicode[STIX]{x1D714}}_{VM}(k_{\Vert }\unicode[STIX]{x1D70C}_{i},k_{\bot }\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e},v_{ti}/c)$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). In the gyrokinetic limit of non-relativistic (
$v_{ti}/c\ll 1$
), low-frequency (
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{i}\ll 1$
), anisotropic (
$k_{\Vert }/k_{\bot }\ll 1$
) fluctuations, the complex eigenfrequency of the linear collisionless gyrokinetic dispersion relation has just three dimensionless parameters when normalized by
$k_{\Vert }$
, where we denote this normalization with an overbar,
$\overline{\unicode[STIX]{x1D714}}\equiv \unicode[STIX]{x1D714}/(k_{\Vert }v_{A})$
; with this normalization, one obtains
$\unicode[STIX]{x1D714}/(k_{\Vert }v_{A})=\overline{\unicode[STIX]{x1D714}}_{GK}(k_{\bot }\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). When the complex eigenfrequency and complex Fourier coefficients of the eigenfunction in gyrokinetics are normalized in this way, they are independent of the parallel wavenumber
$k_{\Vert }$
, so that the phase and amplitude relationships among the different components of the eigenfunction are independent of the parallel wavenumber or coordinate.
Consider, for example, the procedure for initializing an Alfvén wavepacket localized along the direction parallel to the equilibrium magnetic field
$\boldsymbol{B}_{0}=B_{0}\hat{\boldsymbol{z}}$
. For a perpendicular Fourier component of that wavepacket with a wavevector
$(k_{x},k_{y})$
, we specify the complex perpendicular Fourier coefficient of the
$y$
component of the perturbed magnetic field by
$\unicode[STIX]{x1D6FF}\hat{B}_{y}(k_{x},k_{y},z)$
. To obtain the complex perpendicular Fourier coefficient of any other component of the eigenfunction, for example the parallel magnetic field perturbation,
$\unicode[STIX]{x1D6FF}\hat{B}_{z}(k_{x},k_{y},z)$
, we simply multiply the ratio of the suitably normalized linear eigenfunction components,
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\hat{B}_{z}(k_{x},k_{y},z)=\left[\frac{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{z}(k_{x},k_{y},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})}{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{y}(k_{x},k_{y},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})}\right]\unicode[STIX]{x1D6FF}\hat{B}_{y}(k_{x},k_{y},z).\end{eqnarray}$$
The key property of gyrokinetics that we exploit is the fact that the ratio in brackets, determined from the linear eigenfunction, is independent of the parallel wavenumber
$k_{z}$
and parallel coordinate
$z$
. For simplicity, we suppress the dependence in the plasma parameters
$(\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})$
below, as they are constants for a given calculation.
To demonstrate that the linear eigenfunction derived for a given perpendicular wavevector
$(k_{x},k_{y})$
can be used to construct a wavepacket of arbitrary functional form in
$z$
, we note that the Fourier transform in
$z$
of a component of the fluctuating magnetic field can be expressed as
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\hat{B}_{j}(k_{x},k_{y},z)=\mathop{\sum }_{k_{z}}\unicode[STIX]{x1D6FF}\hat{B}_{j}(k_{x},k_{y},k_{z})\text{e}^{\text{i}k_{z}z},\end{eqnarray}$$
where the index
$j$
denotes any component
$x$
,
$y$
or
$z$
. By substituting (A 2) into the left-hand side of (A 1) for
$\unicode[STIX]{x1D6FF}\hat{B}_{z}(k_{x},k_{y},z)$
and right-hand side of (A 1) for
$\unicode[STIX]{x1D6FF}\hat{B}_{y}(k_{x},k_{y},z)$
, we obtain
$$\begin{eqnarray}\mathop{\sum }_{k_{z}}\unicode[STIX]{x1D6FF}\hat{B}_{z}(k_{x},k_{y},k_{z})\text{e}^{\text{i}k_{z}z}=\mathop{\sum }_{k_{z}}\left[\frac{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{z}(k_{x},k_{y})}{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{y}(k_{x},k_{y})}\right]\unicode[STIX]{x1D6FF}\hat{B}_{y}(k_{x},k_{y},k_{z})\text{e}^{\text{i}k_{z}z},\end{eqnarray}$$
where we have exploited the fact that the factor in brackets is independent of
$k_{z}$
to bring it inside of the summation on the right-hand side. The orthogonality of basis functions
$\text{e}^{\text{i}k_{z}z}$
means that the corresponding terms in the sum must be equal, yielding the result
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\hat{B}_{j}(k_{x},k_{y},k_{z})=\left[\frac{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{z}(k_{x},k_{y},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})}{\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{y}(k_{x},k_{y},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})}\right]\unicode[STIX]{x1D6FF}\hat{B}_{y}(k_{x},k_{y},k_{z}).\end{eqnarray}$$
Therefore, the phase and amplitude relationships between different components of the eigenfunction are the same whether the parallel dependence is expressed in coordinate space
$z$
or Fourier space
$k_{z}$
.
The procedure for initializing a localized wavepacket in AstroGK with an arbitrary functional form in the parallel direction
$z$
therefore follows: (i) the form of the wavepacket in the parallel direction
$z$
for the perpendicular Fourier component of the parallel vector potential
$\unicode[STIX]{x1D6FF}\hat{A}_{\Vert }(k_{x},k_{y},z)$
is specified; (ii) the linear collisionless gyrokinetic dispersion relation
$\overline{\unicode[STIX]{x1D714}}_{GK}(k_{\bot }\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D6FD}_{i},T_{i}/T_{e})$
is solved for the other suitably normalized electromagnetic field potentials
$\hat{\overline{\unicode[STIX]{x1D719}}}(k_{x},k_{y})$
and
$\unicode[STIX]{x1D6FF}\hat{\overline{B}}_{\Vert }(k_{x},k_{y})$
as well as the perturbed ion and electron gyrokinetic distribution functions,
$\hat{\overline{h}}_{i}(v_{\Vert },v_{\bot },k_{x},k_{y})$
and
$\hat{\overline{h}}_{e}(v_{\Vert },v_{\bot },k_{x},k_{y})$
; and (iii) the ratio of the suitably normalized eigenfunctions are used to compute the form of the wavepacket in the parallel direction
$z$
for the perpendicular Fourier component of all the other components of the eigenfunction, for example
$\unicode[STIX]{x1D6FF}\hat{B}_{\Vert }(k_{x},k_{y},z)$
. This completes the specification of a wavepacket of arbitrary parallel functional dependence for the chosen linear gyrokinetic wave mode.
A.2 Specification of windowing function
To localize the Alfvén wavepacket, we use a windowing function
$w(z)$
for the complex Fourier wave amplitude of each perpendicular Fourier mode. The windowing function in
$z$
for a given perpendicular Fourier mode is
$$\begin{eqnarray}w(z)=\exp \left[-4\left(\frac{z-z_{0}}{\unicode[STIX]{x1D6E5}_{z}}\right)^{p}\right]+\exp \left[-4\left(\frac{z-z_{0}+L_{z}}{\unicode[STIX]{x1D6E5}_{z}}\right)^{p}\right]+\exp \left[-4\left(\frac{z-z_{0}-L_{z}}{\unicode[STIX]{x1D6E5}_{z}}\right)^{p}\right],\end{eqnarray}$$
where the three window function parameters are the centre of the window
$z_{0}$
, the width of the window
$\unicode[STIX]{x1D6E5}_{z}$
and the power
$p$
of the exponential. Note that the second and third terms are needed to ensure periodicity in
$z$
when the window does not fall to zero at the
$z$
limits of the domain (it is important, since only two terms are included, that the window does fall to zero by at least an additional distance
$L_{z}$
beyond each
$z$
boundary).
The sinusoidal variation in
$z$
of each perpendicular Fourier mode is given by
$$\begin{eqnarray}f(z)=\cos (k_{z}z+\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
where
$k_{z}$
is the wavenumber along the equilibrium magnetic field and
$\unicode[STIX]{x1D6FF}$
is a phase shift for that mode. The total initial waveform along
$z$
is then given by the product of the sinusoidal mode and the windowing function,
$w(z)f(z)$
.
For the localized Alfvén wavepacket collision simulation presented in this paper, the parameters for the dipolar wave (which propagates in the
$-z$
direction) are
$k_{z}a_{0}=-3$
,
$\unicode[STIX]{x1D6FF}=0$
,
$z_{0}=(\unicode[STIX]{x03C0}/2)a_{0}=L_{\Vert }/4$
,
$\unicode[STIX]{x1D6E5}_{z}=1.2a_{0}$
and the default power
$p=2$
. For the unipolar wave (which propagates in the
$+z$
direction), the parameters are
$k_{z}a_{0}=+1$
,
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x03C0}/2$
,
$z_{0}=(-\unicode[STIX]{x03C0}/2)a_{0}=-L_{\Vert }/4$
,
$\unicode[STIX]{x1D6E5}_{z}=1.2a_{0}$
and the default power
$p=2$
. Note that the non-zero phase
$\unicode[STIX]{x1D6FF}$
for this unipolar wavepacket means it has an initial form
$-\sin (k_{z}z)$
.
Note that the aspect ratio of the characteristic perpendicular length scale to the characteristic parallel length scale
$\unicode[STIX]{x1D70C}_{i}/a_{0}\equiv \unicode[STIX]{x1D716}\ll 1$
is the small gyrokinetic expansion parameter. The parallel domain scale is given by
$k_{\Vert }a_{0}=1$
, where the parallel domain length
$L_{\Vert }=2\unicode[STIX]{x03C0}/k_{\Vert }$
, so the domain length can also be expressed as
$L_{\Vert }=2\unicode[STIX]{x03C0}a_{0}$
. All parallel length scales in AstroGK are normalized by
$a_{0}$
, whereas all perpendicular length scales are normalized by
$\unicode[STIX]{x1D70C}_{i}$
, or equivalently dimensionless perpendicular wavenumber
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/S0022377817001003.
