1. Introduction
In this lecture note, we discuss a Monte Carlo particle-in-cell (PIC) finite-element method based on the description of the equations of motion by a Lagrangian derived using the particle-trajectories approach. Starting from the Lagrangian introduced by Low (Reference Low1958), Sugama (Reference Sugama2000) derived the gyrokinetic field theoretic Lagrangian that will be the base of our formulation. For the discretisation, we follow the procedure first proposed by Lewis (Reference Lewis1970) to derive a PIC approximation based on a discrete Lagrangian, the variations of which are used to obtain the time-continuous equations of motion for the particles and the finite-element approximation of the fields. This feature implies a certain number of conservation properties thanks to the Noether theorem for the semi-discretised system. For these to be retained exactly after time discretisation, special care needs to be taken, implying implicit methods. This is inconvenient for large PIC simulations and is generally not done in practice.
Classical derivations of the PIC method are based on the approximate distribution function being a sum of
![]() ${\it\delta}$
functions. A detailed discussion of the method and a systematic derivation of the relevant equations were given by Hu & Krommes (Reference Hu and Krommes1994). Unlike the classical derivation, we cast the PIC method from the beginning into the framework of Monte Carlo simulation, which is best adapted to the study of its approximation properties. This approach enables us to draw on the extensive literature on Monte Carlo methods in statistics to propose efficient noise-reduction strategies. The aim of this lecture note, which follows a large literature on PIC methods for gyrokinetics like Aydemir (Reference Aydemir1994), Hu & Krommes (Reference Hu and Krommes1994), Tran et al. (Reference Tran, Appert, Fivaz, Jost, Vaclavik and Villard1999), Allfrey & Hatzky (Reference Allfrey and Hatzky2003), Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007), Krommes (Reference Krommes2007), Bottino et al. (Reference Bottino, Scott, Brunner, McMillan, Tran, Vernay, Villard, Jolliet, Hatzky and Peeters2010), Kleiber et al. (Reference Kleiber, Hatzky, Könies, Kauffmann and Helander2011) and many others, is to highlight on the one hand the semi-discrete variational principle on which these methods are based and on the other hand the Monte Carlo framework, in order to make a clear link with the Monte Carlo literature in statistics. The outline of the note is the following. First we will introduce the gyrokinetic approximation and in particular the phase-space Lagrangian density on which it is based, derive the gyrokinetic Vlasov–Poisson equations and also present the special case of adiabatic electrons. Then we will describe our finite-element Monte Carlo particle-in-cell discretisation the principle of which consists in obtaining a discrete Lagrangian by applying a Monte Carlo approximation in the particle part of the Lagrangian density and a finite-element approximation for the fields. The PIC marker equations of motion and the discrete field equations then are obtained as the Euler–Lagrange equations of the discrete Lagrangian. We will then explain how classical Monte Carlo noise-reduction techniques can be applied. Finally, in the last part we will present some typical gyrokinetic simulations and illustrate how the noise-to-signal ratio can be monitored in a PIC simulation.
${\it\delta}$
functions. A detailed discussion of the method and a systematic derivation of the relevant equations were given by Hu & Krommes (Reference Hu and Krommes1994). Unlike the classical derivation, we cast the PIC method from the beginning into the framework of Monte Carlo simulation, which is best adapted to the study of its approximation properties. This approach enables us to draw on the extensive literature on Monte Carlo methods in statistics to propose efficient noise-reduction strategies. The aim of this lecture note, which follows a large literature on PIC methods for gyrokinetics like Aydemir (Reference Aydemir1994), Hu & Krommes (Reference Hu and Krommes1994), Tran et al. (Reference Tran, Appert, Fivaz, Jost, Vaclavik and Villard1999), Allfrey & Hatzky (Reference Allfrey and Hatzky2003), Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007), Krommes (Reference Krommes2007), Bottino et al. (Reference Bottino, Scott, Brunner, McMillan, Tran, Vernay, Villard, Jolliet, Hatzky and Peeters2010), Kleiber et al. (Reference Kleiber, Hatzky, Könies, Kauffmann and Helander2011) and many others, is to highlight on the one hand the semi-discrete variational principle on which these methods are based and on the other hand the Monte Carlo framework, in order to make a clear link with the Monte Carlo literature in statistics. The outline of the note is the following. First we will introduce the gyrokinetic approximation and in particular the phase-space Lagrangian density on which it is based, derive the gyrokinetic Vlasov–Poisson equations and also present the special case of adiabatic electrons. Then we will describe our finite-element Monte Carlo particle-in-cell discretisation the principle of which consists in obtaining a discrete Lagrangian by applying a Monte Carlo approximation in the particle part of the Lagrangian density and a finite-element approximation for the fields. The PIC marker equations of motion and the discrete field equations then are obtained as the Euler–Lagrange equations of the discrete Lagrangian. We will then explain how classical Monte Carlo noise-reduction techniques can be applied. Finally, in the last part we will present some typical gyrokinetic simulations and illustrate how the noise-to-signal ratio can be monitored in a PIC simulation.
2. Description of the gyrokinetic model
Gyrokinetic (GK) theory aims to describe plasma particle motion in terms of drifts of particle gyrocentres, rather than the usual combination of gyromotion and drifts of the particles, thus reducing the original 6D kinetic problem into a 5D problem. The development of GK theory was motivated by the need to describe complex plasma dynamics over time scales much longer than the short gyromotion time scale. The typical example is the study of the low-frequency electromagnetic fluctuations (microturbulence) observed in inhomogeneous magnetised plasmas, characterised by
![]() ${\it\Omega}<{\it\Omega}_{s}$
, where
${\it\Omega}<{\it\Omega}_{s}$
, where
![]() ${\it\Omega}_{s}=e_{s}B/m_{s}$
is the ion cyclotron frequency.
${\it\Omega}_{s}=e_{s}B/m_{s}$
is the ion cyclotron frequency.
Several ways to construct gyrokinetic equations exist. Initially, GK equations were derived by gyroaveraging the Vlasov equation with recursive methods (see for example Frieman & Chen Reference Frieman and Chen1982 and Lee Reference Lee1983). Modern gyrokinetic theory is based on a Hamiltonian representation in which nonlinear gyrokinetic equations are derived from a systematic Hamiltonian theory, as originally proposed by Dubin et al. (Reference Dubin, Krommes, Oberman and Lee1983). The starting point of the derivation is the description of particle motion in a magnetic field in terms of a drift-kinetic Lagrangian. Gyrokinetic equations can be constructed when this Lagrangian is (Lie) transformed into a low-frequency form by means of an expansion based on a small parameter. The small parameter can be either the fluctuation amplitude of the drifts (Littlejohn Reference Littlejohn1981, Reference Littlejohn1983) or the gyroradius compared to the dynamical scale lengths (Hahm Reference Hahm1988). In this formulation, a back transformation was used to obtain the self-consistent field equations for the potential (Dubin et al. Reference Dubin, Krommes, Oberman and Lee1983; Hahm Reference Hahm1988). In modern gyrokinetics, the so-called gyrokinetic field theory, the entire Lagrangian is constructed as the integral of a Lagrangian density, with the field equations obtained as the Euler–Lagrange equations by varying the potentials in the Lagrangian (Brizard Reference Brizard2000; Sugama Reference Sugama2000). These two approaches have been proved to be identical by Brizard & Hahm (Reference Brizard and Hahm2007) and both preserve the symmetry and conservation properties of the Vlasov equation.
Gyrokinetic field theory can be addressed in the context of a general Hamiltonian (Scott & Smirnov Reference Scott and Smirnov2010). It consists in constructing a Lagrangian in which all the dependence on dynamical variables is in the Hamiltonian or in the free field terms. The symmetry with time through the Hamiltonian leads automatically to energy conservation. Indeed, self-consistent nonlinear gyrokinetic Vlasov–Maxwell equations can be derived starting from the Lagrangian, without any additional ordering assumption. This approach also naturally provides the exact energy conservation law these nonlinear GK equations satisfy and it is therefore particularly suited for numerical simulations. In the following, the simplest self-consistent and energy conserving gyrokinetic model, suited for gyrokinetic PIC simulations, is derived using general Hamiltonian-based gyrokinetic field theory.
2.1. Gyrokinetic Lagrangian
As a starting point, the following Lie-transformed low-frequency particle Lagrangian is assumed:
The velocity variables are the magnetic moment
![]() ${\it\mu}\equiv mv_{\bot }^{2}/(2B)$
, the canonical parallel momentum
${\it\mu}\equiv mv_{\bot }^{2}/(2B)$
, the canonical parallel momentum
![]() $p_{\Vert }$
and the gyroangle
$p_{\Vert }$
and the gyroangle
![]() ${\it\theta}$
;
${\it\theta}$
;
![]() $\boldsymbol{R}$
is the gyrocentre position. Upper dots denote total time derivatives. The perpendicular subscript denotes the component in the plane perpendicular to the background magnetic field
$\boldsymbol{R}$
is the gyrocentre position. Upper dots denote total time derivatives. The perpendicular subscript denotes the component in the plane perpendicular to the background magnetic field
![]() $\boldsymbol{B}=\boldsymbol{{\rm\nabla}}\times \unicode[STIX]{x1D63C}$
. Note that the symplectic part depends only on the background, while all the time-varying fields are contained in the Hamiltonian
$\boldsymbol{B}=\boldsymbol{{\rm\nabla}}\times \unicode[STIX]{x1D63C}$
. Note that the symplectic part depends only on the background, while all the time-varying fields are contained in the Hamiltonian
![]() $H$
. In the sequel,
$H$
. In the sequel,
![]() $\boldsymbol{A}$
will always denote the background vector potential, whereas
$\boldsymbol{A}$
will always denote the background vector potential, whereas
![]() $A_{\Vert }$
will denote the parallel component of the fluctuating field, the perpendicular part being assumed to be zero. Complete derivations of such a particle Lagrangian can be found, for example, in Hahm (Reference Hahm1988), Brizard & Hahm (Reference Brizard and Hahm2007) and Miyato, Scott & Strintzi (Reference Miyato, Scott and Strintzi2009). Following Sugama (Reference Sugama2000), the gyrokinetic total Lagrangian is given by
$A_{\Vert }$
will denote the parallel component of the fluctuating field, the perpendicular part being assumed to be zero. Complete derivations of such a particle Lagrangian can be found, for example, in Hahm (Reference Hahm1988), Brizard & Hahm (Reference Brizard and Hahm2007) and Miyato, Scott & Strintzi (Reference Miyato, Scott and Strintzi2009). Following Sugama (Reference Sugama2000), the gyrokinetic total Lagrangian is given by
where
![]() $\boldsymbol{Z}\equiv (\boldsymbol{R},p_{\Vert },{\it\mu},{\it\theta})$
,
$\boldsymbol{Z}\equiv (\boldsymbol{R},p_{\Vert },{\it\mu},{\it\theta})$
,
![]() $\text{d}W\equiv (2{\rm\pi}/m^{2})B_{\Vert }^{\ast }\,\text{d}p_{\Vert }\,\text{d}{\it\mu}$
and
$\text{d}W\equiv (2{\rm\pi}/m^{2})B_{\Vert }^{\ast }\,\text{d}p_{\Vert }\,\text{d}{\it\mu}$
and
![]() $\text{d}V$
denotes the volume element in physical space, with Jacobian
$\text{d}V$
denotes the volume element in physical space, with Jacobian
![]() $1/\sqrt{g}$
. Here
$1/\sqrt{g}$
. Here
![]() $f(\boldsymbol{Z}_{0})$
is the distribution function for the species
$f(\boldsymbol{Z}_{0})$
is the distribution function for the species
![]() $sp$
at an arbitrary initial time
$sp$
at an arbitrary initial time
![]() $t_{0}$
. We will not use a specific notation to distinguish the distribution functions of the different species for simplicity. Here
$t_{0}$
. We will not use a specific notation to distinguish the distribution functions of the different species for simplicity. Here
![]() $\text{d}W_{0}$
implies that the phase-space Jacobian is a function of
$\text{d}W_{0}$
implies that the phase-space Jacobian is a function of
![]() $\boldsymbol{Z}_{0}$
, i.e.
$\boldsymbol{Z}_{0}$
, i.e.
![]() $B_{\Vert }^{\ast }(\boldsymbol{Z}_{0})$
. The quantity
$B_{\Vert }^{\ast }(\boldsymbol{Z}_{0})$
. The quantity
![]() $L_{p}$
is the Lie-transformed particle Lagrangian of (2.1), written in terms of the gyrocentre coordinates of the particle, with the initial condition
$L_{p}$
is the Lie-transformed particle Lagrangian of (2.1), written in terms of the gyrocentre coordinates of the particle, with the initial condition
The first term in the total Lagrangian is the Lagrangian for charged particles. Note that here the integral is performed with respect to
![]() $\boldsymbol{Z}_{0}$
: it is therefore assumed that the particles can be traced back in time to their positions at
$\boldsymbol{Z}_{0}$
: it is therefore assumed that the particles can be traced back in time to their positions at
![]() $t_{0}$
. The second term is the Lagrangian for the electromagnetic fields.
$t_{0}$
. The second term is the Lagrangian for the electromagnetic fields.
Writing that the distribution function is conserved along the particle trajectories
yields the GK Vlasov equation by taking the time derivative:
The particle-number conservation follows from Liouville’s theorem for a time-independent Jacobian:
which is a property inherited from the particle Lagrangian
![]() $L_{p}$
that we shall verify later. Then, on the one hand the first integral defining
$L_{p}$
that we shall verify later. Then, on the one hand the first integral defining
![]() $L$
can be expressed by the change of variables
$L$
can be expressed by the change of variables
![]() $\boldsymbol{Z}=\boldsymbol{Z}(\boldsymbol{Z}_{0},t_{0};t)$
as
$\boldsymbol{Z}=\boldsymbol{Z}(\boldsymbol{Z}_{0},t_{0};t)$
as
and the Vlasov equation can be written in the conservative form
The GK Hamiltonian in general depends on the electrostatic potentials
![]() ${\it\Phi}$
and on the parallel component of the fluctuation magnetic potential
${\it\Phi}$
and on the parallel component of the fluctuation magnetic potential
![]() $A_{\Vert }$
. In its simplest form, the GK Hamiltonian has the following form:
$A_{\Vert }$
. In its simplest form, the GK Hamiltonian has the following form:
The last term in the Hamiltonian is the negative of the kinetic energy associated to the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
motion of the gyrocentres. The physical meaning and implications of this term are specifically addressed in a recent paper by Krommes (Reference Krommes2013). A derivation of the gyrokinetic equations using a higher order Hamiltonian can be found, for example, in Miyato & Scott (Reference Miyato and Scott2013). Note that
$\boldsymbol{E}\times \boldsymbol{B}$
motion of the gyrocentres. The physical meaning and implications of this term are specifically addressed in a recent paper by Krommes (Reference Krommes2013). A derivation of the gyrokinetic equations using a higher order Hamiltonian can be found, for example, in Miyato & Scott (Reference Miyato and Scott2013). Note that
![]() $U$
, the parallel velocity, is not a coordinate. It is defined by
$U$
, the parallel velocity, is not a coordinate. It is defined by
![]() $mU=p_{\Vert }-(e/c)\text{J}_{0}A_{\Vert }$
and is a function of the fluctuation magnetic potential
$mU=p_{\Vert }-(e/c)\text{J}_{0}A_{\Vert }$
and is a function of the fluctuation magnetic potential
![]() $A_{\Vert }$
. The gyroaveraging operator
$A_{\Vert }$
. The gyroaveraging operator
![]() $\text{J}_{0}$
applied to an arbitrary function
$\text{J}_{0}$
applied to an arbitrary function
![]() ${\it\psi}$
in configuration space is defined by
${\it\psi}$
in configuration space is defined by
where
![]() ${\bf\rho}$
is the vector going from the guiding centre position to the particle position. It depends on
${\bf\rho}$
is the vector going from the guiding centre position to the particle position. It depends on
![]() ${\it\mu}$
and spatial coordinates. In the context of GK field theory, this Lagrangian can be further approximated without losing self-consistency and energetic consistency of the final equations (Sugama Reference Sugama2000; Scott & Smirnov Reference Scott and Smirnov2010). A possible approximation, widely used in GK simulations, is the so-called quasi-neutrality approximation. It consists in neglecting the term proportional to
${\it\mu}$
and spatial coordinates. In the context of GK field theory, this Lagrangian can be further approximated without losing self-consistency and energetic consistency of the final equations (Sugama Reference Sugama2000; Scott & Smirnov Reference Scott and Smirnov2010). A possible approximation, widely used in GK simulations, is the so-called quasi-neutrality approximation. It consists in neglecting the term proportional to
![]() $E^{2}$
in the free field term. This term is ordered small compared to the so-called
$E^{2}$
in the free field term. This term is ordered small compared to the so-called
![]() $E\times B$
energy, corresponding to the second-order term in
$E\times B$
energy, corresponding to the second-order term in
![]() ${\it\Phi}$
in the Hamiltonian:
${\it\Phi}$
in the Hamiltonian:
having introduced the electron Debye length squared
![]() ${\it\lambda}_{d}^{2}\equiv (k_{B}T_{e})/(4{\rm\pi}ne^{2})$
and the ion sound Larmor radius
${\it\lambda}_{d}^{2}\equiv (k_{B}T_{e})/(4{\rm\pi}ne^{2})$
and the ion sound Larmor radius
![]() ${\it\rho}_{S}^{2}\equiv (k_{B}T_{e}mc^{2})/(e^{2}B^{2})$
;
${\it\rho}_{S}^{2}\equiv (k_{B}T_{e}mc^{2})/(e^{2}B^{2})$
;
![]() $\text{d}{\it\Omega}\equiv \text{d}V\,\text{d}W$
.
$\text{d}{\it\Omega}\equiv \text{d}V\,\text{d}W$
.
In fusion plasmas
where
![]() $v_{a}$
is the Alfvén velocity and
$v_{a}$
is the Alfvén velocity and
![]() $E_{\Vert }^{2}$
is even smaller. Therefore, the
$E_{\Vert }^{2}$
is even smaller. Therefore, the
![]() $E^{2}$
term can be safely neglected. We will see in the following that this approximation will lead to a field equation for the electrostatic potential equivalent to a quasi-neutrality condition.
$E^{2}$
term can be safely neglected. We will see in the following that this approximation will lead to a field equation for the electrostatic potential equivalent to a quasi-neutrality condition.
Recalling the definition of
![]() $p_{\Vert }$
, the GK Hamiltonian can be rewritten as follows:
$p_{\Vert }$
, the GK Hamiltonian can be rewritten as follows:
 $$\begin{eqnarray}\displaystyle L & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\left(\left(\frac{e}{c}\boldsymbol{A}+p_{\Vert }\boldsymbol{b}\right)\boldsymbol{\cdot }\dot{\boldsymbol{R}}+\frac{mc}{e}{\it\mu}\dot{{\it\theta}}-H_{0}-H_{1}\right)f\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,H_{2}f_{M}-\int \text{d}V\,\frac{B_{\bot }^{2}}{8{\rm\pi}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\left(\left(\frac{e}{c}\boldsymbol{A}+p_{\Vert }\boldsymbol{b}\right)\boldsymbol{\cdot }\dot{\boldsymbol{R}}+\frac{mc}{e}{\it\mu}\dot{{\it\theta}}-H_{0}-H_{1}\right)f\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,H_{2}f_{M}-\int \text{d}V\,\frac{B_{\bot }^{2}}{8{\rm\pi}}.\end{eqnarray}$$
Since this approximation leads to linearised field equations, it is traditionally known as the linearised polarisation approximation. However, this choice of Lagrangian has a deeper meaning: already Sugama (Reference Sugama2000) showed that in order to construct a gyrokinetic equation based on first-order drift motion, only
![]() $H_{0}+H_{1}$
must multiply
$H_{0}+H_{1}$
must multiply
![]() $f$
, thus contributing to the drifts via the variational derivatives. The term containing
$f$
, thus contributing to the drifts via the variational derivatives. The term containing
![]() $H_{2}$
must act as a field term and should contribute to the field equations only, i.e.
$H_{2}$
must act as a field term and should contribute to the field equations only, i.e.
![]() $H_{2}\,f$
must be replaced by
$H_{2}\,f$
must be replaced by
![]() $H_{2}\,f_{0}$
. Conversely, if one desires to keep the dependent variable
$H_{2}\,f_{0}$
. Conversely, if one desires to keep the dependent variable
![]() $f$
in this term then
$f$
in this term then
![]() $H_{2}$
must be kept in the drift motion. This is the basic statement of energetic consistency in a gyrokinetic global model as discussed in Scott & Smirnov (Reference Scott and Smirnov2010). Note that this result was already present in both Brizard (Reference Brizard2000) and Sugama (Reference Sugama2000). In addition to this, Miyato et al. (Reference Miyato, Scott and Strintzi2009) showed that the reduced magnetohydrodynamic (MHD) vorticity equation can be recovered by taking the time derivative,
$H_{2}$
must be kept in the drift motion. This is the basic statement of energetic consistency in a gyrokinetic global model as discussed in Scott & Smirnov (Reference Scott and Smirnov2010). Note that this result was already present in both Brizard (Reference Brizard2000) and Sugama (Reference Sugama2000). In addition to this, Miyato et al. (Reference Miyato, Scott and Strintzi2009) showed that the reduced magnetohydrodynamic (MHD) vorticity equation can be recovered by taking the time derivative,
![]() $\partial /\partial t$
, of the linearised polarisation equation.
$\partial /\partial t$
, of the linearised polarisation equation.
Although electromagnetic effects are important to correctly describe experimental plasmas, in the following we will neglect magnetic perturbations, setting
![]() $A_{\Vert }=0$
, which implies that
$A_{\Vert }=0$
, which implies that
![]() $B_{\bot }^{2}=0$
and
$B_{\bot }^{2}=0$
and
![]() $p_{\Vert }=mU$
.
$p_{\Vert }=mU$
.
Finally, the electrostatic GK Lagrangian starting point for the derivation of our GK system is
It is important to underline that from now on, any additional approximation or ordering will break the symmetry and conservation properties of the underlying dynamical system.
2.2. Gyrokinetic electrostatic Vlasov–Poisson equations
The gyrokinetic equations for the particle distribution function and the GK field equations can be derived from the GK Lagrangian using variational principles for the action functional
![]() $I$
(Sugama Reference Sugama2000):
$I$
(Sugama Reference Sugama2000):
where the functional derivative of
![]() $L$
with respect to a function
$L$
with respect to a function
![]() ${\it\psi}$
is defined for an arbitrary variation
${\it\psi}$
is defined for an arbitrary variation
![]() ${\it\delta}{\it\psi}$
in the same function space as
${\it\delta}{\it\psi}$
in the same function space as
![]() ${\it\psi}$
by
${\it\psi}$
by
The particle equations of motion can be obtained by taking the functional derivatives with respect to the particle phase-space positions:
![]() $\boldsymbol{Z}=(\boldsymbol{R},p_{\Vert },{\it\mu})$
:
$\boldsymbol{Z}=(\boldsymbol{R},p_{\Vert },{\it\mu})$
:
as
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
are arbitrary. This yields the GK Euler–Lagrange equations for the particle Lagrangian
$t_{2}$
are arbitrary. This yields the GK Euler–Lagrange equations for the particle Lagrangian
![]() $L_{p}$
, describing the drift motion of the gyrocentres, which can be expressed as
$L_{p}$
, describing the drift motion of the gyrocentres, which can be expressed as
for all the phase-space components
![]() $y$
. We follow here the idea introduced by Littlejohn (Reference Littlejohn1983) for non-canonical formulations. Let us first compute all the needed partial derivatives of
$y$
. We follow here the idea introduced by Littlejohn (Reference Littlejohn1983) for non-canonical formulations. Let us first compute all the needed partial derivatives of
![]() $L_{p}$
, denoting by
$L_{p}$
, denoting by
![]() $\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C}$
the Jacobian matrix associated to the vector field
$\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C}$
the Jacobian matrix associated to the vector field
![]() $\boldsymbol{A}$
:
$\boldsymbol{A}$
:
Taking the time derivative of the first term above, using that
![]() $\boldsymbol{A}$
and
$\boldsymbol{A}$
and
![]() $\boldsymbol{b}$
do not depend on time,
$\boldsymbol{b}$
do not depend on time,
where we introduce
We can now write the Euler–Lagrange equation for
![]() $\boldsymbol{R}$
and
$\boldsymbol{R}$
and
![]() $p_{\Vert }$
:
$p_{\Vert }$
:
Let us introduce
![]() $\boldsymbol{F}=\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C}-(\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C})^{\text{T}}$
with the properties
$\boldsymbol{F}=\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C}-(\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D63C})^{\text{T}}$
with the properties
and similarly
![]() $\boldsymbol{F}^{\ast }=\boldsymbol{{\rm\nabla}}\boldsymbol{A}^{\ast }-(\boldsymbol{{\rm\nabla}}\boldsymbol{A}^{\ast })^{\text{T}}$
, with
$\boldsymbol{F}^{\ast }=\boldsymbol{{\rm\nabla}}\boldsymbol{A}^{\ast }-(\boldsymbol{{\rm\nabla}}\boldsymbol{A}^{\ast })^{\text{T}}$
, with
![]() $\boldsymbol{C}\times \boldsymbol{B}^{\ast }=\boldsymbol{F}^{\ast }\boldsymbol{C}$
for any vector
$\boldsymbol{C}\times \boldsymbol{B}^{\ast }=\boldsymbol{F}^{\ast }\boldsymbol{C}$
for any vector
![]() $\boldsymbol{C}$
. Then, in (2.27), we have
$\boldsymbol{C}$
. Then, in (2.27), we have
and we can write (2.27) equivalently
Finally, taking the dot product of (2.31) with
![]() $\boldsymbol{B}^{\ast }$
yields an equation for
$\boldsymbol{B}^{\ast }$
yields an equation for
![]() ${\dot{p}}_{\Vert }$
and, taking the cross product of
${\dot{p}}_{\Vert }$
and, taking the cross product of
![]() $\boldsymbol{b}$
and (2.31), using that
$\boldsymbol{b}$
and (2.31), using that
![]() $\boldsymbol{b}\times (\dot{\boldsymbol{R}}\times \boldsymbol{B}^{\ast })=(\boldsymbol{B}^{\ast }\boldsymbol{\cdot }\boldsymbol{b})\dot{\boldsymbol{R}}-(\dot{\boldsymbol{R}}\boldsymbol{\cdot }\boldsymbol{b})\boldsymbol{B}^{\ast }$
and (2.28), we get an equation for
$\boldsymbol{b}\times (\dot{\boldsymbol{R}}\times \boldsymbol{B}^{\ast })=(\boldsymbol{B}^{\ast }\boldsymbol{\cdot }\boldsymbol{b})\dot{\boldsymbol{R}}-(\dot{\boldsymbol{R}}\boldsymbol{\cdot }\boldsymbol{b})\boldsymbol{B}^{\ast }$
and (2.28), we get an equation for
![]() $\dot{\boldsymbol{R}}$
. The equations of motion for the gyrocentres then read
$\dot{\boldsymbol{R}}$
. The equations of motion for the gyrocentres then read
Those equations can be cast in a more familiar form by inserting the values of
![]() $H_{0}$
and
$H_{0}$
and
![]() $H_{1}$
:
$H_{1}$
:
We can now check that the Liouville theorem, which is a fundamental property, is verified for the gyrocentre equations of motion (2.32)–(2.33) with Jacobian
![]() $B_{\Vert }^{\ast }$
(we denote
$B_{\Vert }^{\ast }$
(we denote
![]() $H_{e}=H_{0}+H_{1}$
):
$H_{e}=H_{0}+H_{1}$
):
where we made use of
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}^{\ast }=0$
, which is a necessary condition for Liouville’s theorem to be satisfied. As
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}^{\ast }=0$
, which is a necessary condition for Liouville’s theorem to be satisfied. As
![]() $\boldsymbol{B}^{\ast }$
is defined as a curl, this is obviously verified.
$\boldsymbol{B}^{\ast }$
is defined as a curl, this is obviously verified.
The equation for the electrostatic potential, the so-called polarisation equation or GK Poisson equation, is derived by computing the functional derivative of
![]() $L$
(given by (2.18)) with respect to the electrostatic potential and setting it to zero. Let us compute this functional derivative using the definition (2.20). We first notice that the only dependence on
$L$
(given by (2.18)) with respect to the electrostatic potential and setting it to zero. Let us compute this functional derivative using the definition (2.20). We first notice that the only dependence on
![]() ${\it\Phi}$
in the first integral defining
${\it\Phi}$
in the first integral defining
![]() $L$
is in
$L$
is in
![]() $H_{1}=e\text{J}_{0}{\it\Phi}$
in the electrostatic case and, as the gyroaverage operator
$H_{1}=e\text{J}_{0}{\it\Phi}$
in the electrostatic case and, as the gyroaverage operator
![]() $\text{J}_{0}$
is a linear operator of
$\text{J}_{0}$
is a linear operator of
![]() ${\it\Phi}$
, we simply have
${\it\Phi}$
, we simply have
This is the variational formulation sometimes also called the weak form of the polarisation equation that defines the electrostatic potential
![]() ${\it\Phi}$
. This variational formulation can be used directly in a finite-element discretisation, as we will see later. Let us however single out the test function
${\it\Phi}$
. This variational formulation can be used directly in a finite-element discretisation, as we will see later. Let us however single out the test function
![]() ${\it\delta}{\it\Phi}$
to express the polarisation equation in its usual form. For this, we need on the one hand to shift the gyroaverage operator from
${\it\delta}{\it\Phi}$
to express the polarisation equation in its usual form. For this, we need on the one hand to shift the gyroaverage operator from
![]() ${\it\delta}{\it\Phi}$
to
${\it\delta}{\it\Phi}$
to
![]() $f$
; this is done by defining its adjoint operator
$f$
; this is done by defining its adjoint operator
![]() $\text{J}_{0}^{\dagger }$
by
$\text{J}_{0}^{\dagger }$
by
Then, using a Green’s formula in the second integral of (2.38), assuming that
![]() ${\it\Phi}$
vanishes on the boundary and taking out
${\it\Phi}$
vanishes on the boundary and taking out
![]() $B_{\Vert }^{\ast }$
that is hidden in
$B_{\Vert }^{\ast }$
that is hidden in
![]() $\text{d}W$
, we get
$\text{d}W$
, we get
Note that, if one wishes to apply directly
![]() $\text{J}_{0}$
to
$\text{J}_{0}$
to
![]() $f$
instead of the test function, we need
$f$
instead of the test function, we need
![]() $\text{J}_{0}^{\dagger }=\text{J}_{0}$
, which means that
$\text{J}_{0}^{\dagger }=\text{J}_{0}$
, which means that
![]() $\text{J}_{0}$
has to be Hermitian. Such a
$\text{J}_{0}$
has to be Hermitian. Such a
![]() $\text{J}_{0}$
can be constructed as shown in McMillan et al. (Reference McMillan, Hill, Jolliet, Vernay, Villard and Bottino2012) but is not necessary when we work directly on the variational formulation with finite elements, as then
$\text{J}_{0}$
can be constructed as shown in McMillan et al. (Reference McMillan, Hill, Jolliet, Vernay, Villard and Bottino2012) but is not necessary when we work directly on the variational formulation with finite elements, as then
![]() $\text{J}_{0}$
can be applied to the test function
$\text{J}_{0}$
can be applied to the test function
![]() ${\it\delta}{\it\Phi}$
.
${\it\delta}{\it\Phi}$
.
The arbitrariness of
![]() ${\it\delta}{\it\Phi}$
implies that
${\it\delta}{\it\Phi}$
implies that
Since the integral with respect to
![]() $\text{d}p_{\Vert }\text{d}{\it\mu}$
commutes with
$\text{d}p_{\Vert }\text{d}{\it\mu}$
commutes with
![]() $\boldsymbol{{\rm\nabla}}$
, the velocity integral in the second term can be performed, leading to the following linear polarisation equation:
$\boldsymbol{{\rm\nabla}}$
, the velocity integral in the second term can be performed, leading to the following linear polarisation equation:
where
![]() $n_{0}$
is the density associated to the equilibrium Maxwellian
$n_{0}$
is the density associated to the equilibrium Maxwellian
![]() $f_{M}$
.
$f_{M}$
.
The expression of the polarisation equation clarifies the meaning of the approximations made: it is a linear equation and it has the form
![]() $\sum _{sp}en_{sp}=0$
, where
$\sum _{sp}en_{sp}=0$
, where
![]() $en_{sp}$
is the particle charge density, i.e. a quasi-neutrality condition.
$en_{sp}$
is the particle charge density, i.e. a quasi-neutrality condition.
In summary, the GK model used in the following is
Despite all the approximations made, this model is physically relevant and it can be used to describe a large class of micro-instabilities excited by the density and temperature gradients, like ion temperature gradient (ITG) driven modes or trapped electron modes (TEMs).
Thanks to its derivation from a Lagrangian density which does not directly depend on time, there is a conserved energy. In our case the following energy is conserved: (Dubin et al. Reference Dubin, Krommes, Oberman and Lee1983):
Let us verify this by direct computation. As
![]() $H_{0}$
and
$H_{0}$
and
![]() $f_{M}$
do not depend on time,
$f_{M}$
do not depend on time,
We first notice that
so that
On the other hand, we have for each species independently, denoting
![]() $H_{e}=H_{0}+H_{1}$
,
$H_{e}=H_{0}+H_{1}$
,
This follows from the Hamiltonian structure of the Vlasov equation (Poisson brackets), but can also be verified as follows. As
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}^{\ast }=0$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}^{\ast }=0$
and
![]() $\partial \boldsymbol{B}^{\ast }/\partial p_{\Vert }=c/e\boldsymbol{{\rm\nabla}}\times \boldsymbol{b}$
, we have
$\partial \boldsymbol{B}^{\ast }/\partial p_{\Vert }=c/e\boldsymbol{{\rm\nabla}}\times \boldsymbol{b}$
, we have
Integrating over phase space, the terms on the left-hand side vanish. On the other hand,
Then, as
![]() $\int \text{d}V\,\text{d}p_{\Vert }\,\text{d}{\it\mu}\boldsymbol{{\rm\nabla}}H_{e}^{2}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times (f\boldsymbol{b})=0$
, using the GK Vlasov equation, we get
$\int \text{d}V\,\text{d}p_{\Vert }\,\text{d}{\it\mu}\boldsymbol{{\rm\nabla}}H_{e}^{2}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times (f\boldsymbol{b})=0$
, using the GK Vlasov equation, we get
In the electrostatic, quasi-neutral limit that we consider, we have
Then our conserved energy from (2.47) becomes
 $$\begin{eqnarray}\displaystyle \mathscr{E}(t) & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,f\left(m\frac{U^{2}}{2}+{\it\mu}B+e\text{J}_{0}{\it\Phi}\right)-\int \text{d}{\it\Omega}\,f_{M}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}|^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,f\left(m\frac{U^{2}}{2}+{\it\mu}B\right)+\int \text{d}{\it\Omega}\,f_{M}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{E}(t) & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,f\left(m\frac{U^{2}}{2}+{\it\mu}B+e\text{J}_{0}{\it\Phi}\right)-\int \text{d}{\it\Omega}\,f_{M}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}|^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{sp}\int \text{d}{\it\Omega}\,f\left(m\frac{U^{2}}{2}+{\it\mu}B\right)+\int \text{d}{\it\Omega}\,f_{M}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}|^{2}\end{eqnarray}$$
using the variational form of the polarisation equation (2.38) with
![]() ${\it\delta}{\it\Phi}={\it\Phi}$
, which reads
${\it\delta}{\it\Phi}={\it\Phi}$
, which reads
Note that the same relation can be obtained by multiplying the polarisation equation (2.42) by
![]() ${\it\Phi}$
and integrating (by parts) over volume (Scott Reference Scott2010). Because of this last relation, the energy can be written equivalently as
${\it\Phi}$
and integrating (by parts) over volume (Scott Reference Scott2010). Because of this last relation, the energy can be written equivalently as
with
![]() $\mathscr{E}_{F}\equiv 1/2\sum _{sp}\int \text{d}{\it\Omega}\,ef\text{J}_{0}{\it\Phi}$
.
$\mathscr{E}_{F}\equiv 1/2\sum _{sp}\int \text{d}{\it\Omega}\,ef\text{J}_{0}{\it\Phi}$
.
The power balance equation, also called the
![]() $E\times B$
-thermal transfer equation, is
$E\times B$
-thermal transfer equation, is
It can be verified, using the Euler–Lagrange equations, that
where
![]() $\boldsymbol{R}_{0}$
represents the part of (2.44) which does not contain terms in
$\boldsymbol{R}_{0}$
represents the part of (2.44) which does not contain terms in
![]() ${\it\Phi}$
. This quantity can be compared to the time derivative of the field energy:
${\it\Phi}$
. This quantity can be compared to the time derivative of the field energy:
In numerical simulations it is particularly useful to consider the following form of the power balance equation:
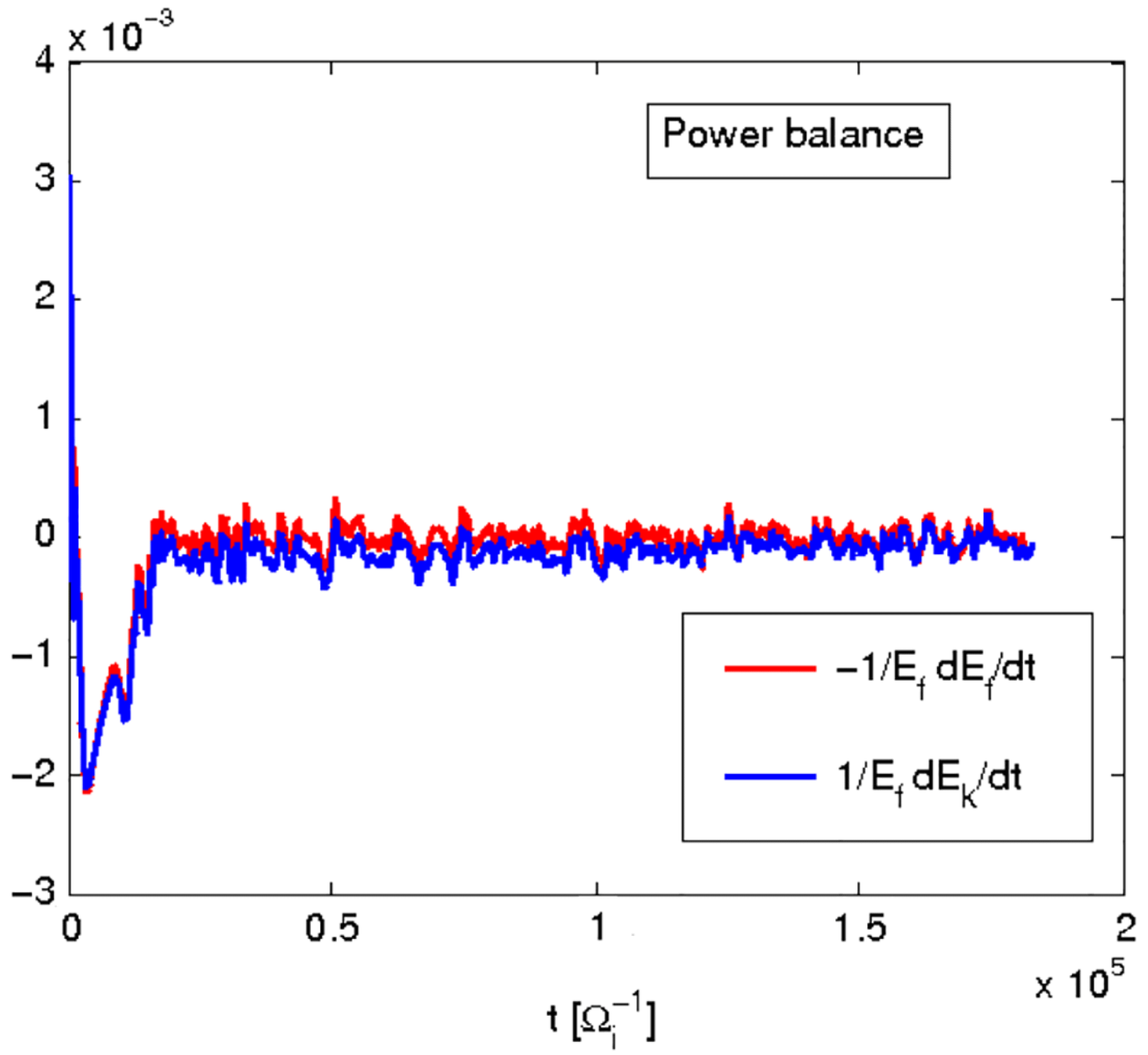
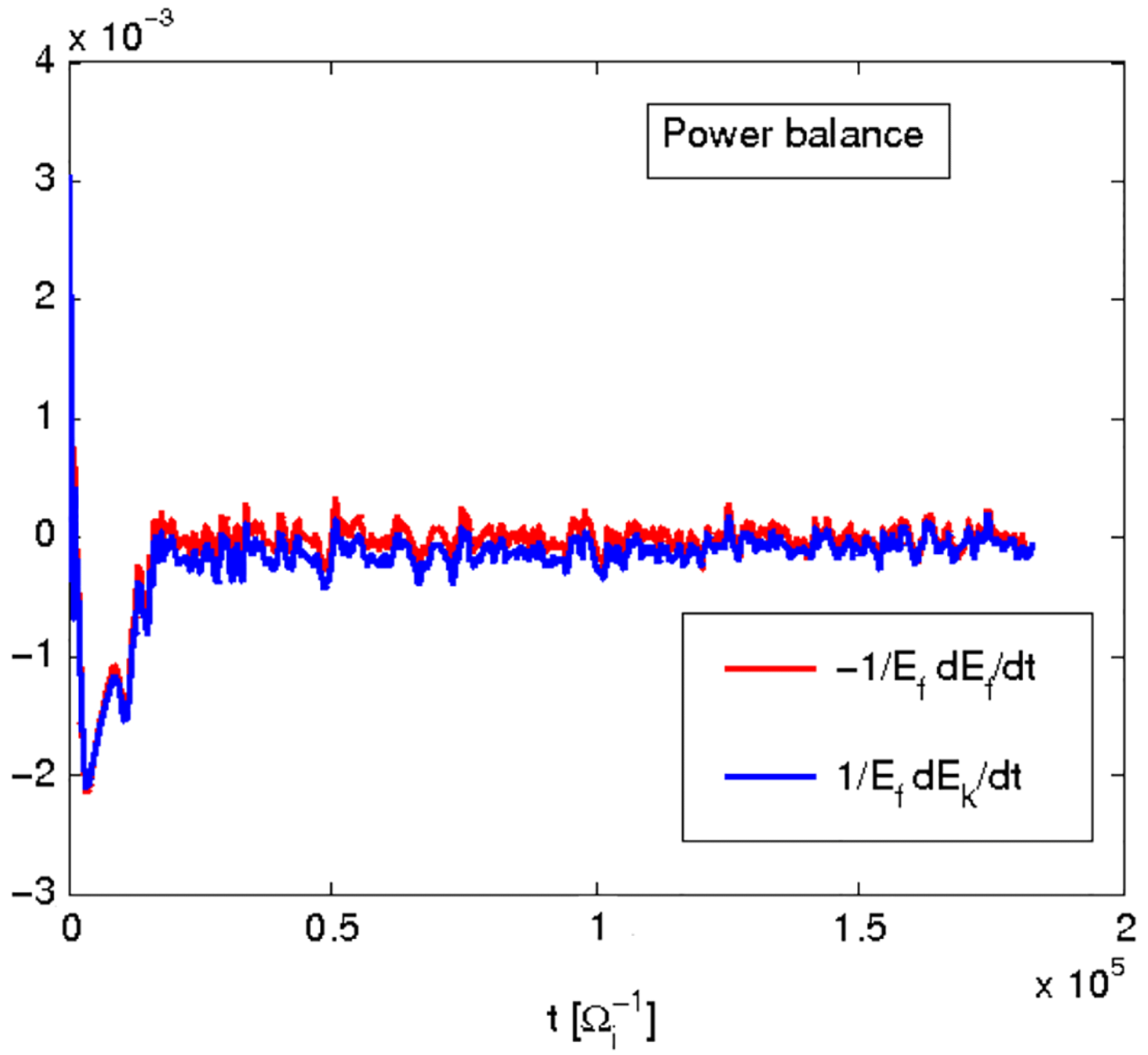
Figure 1 shows an example of power balance in a global nonlinear gyrokinetic simulation, for the Cyclone base section described in § 4. The power balance equation not only gives an indication of the quality of the simulation, but also provides, in linear simulations, a measure of the instantaneous growth rate as
Hence,
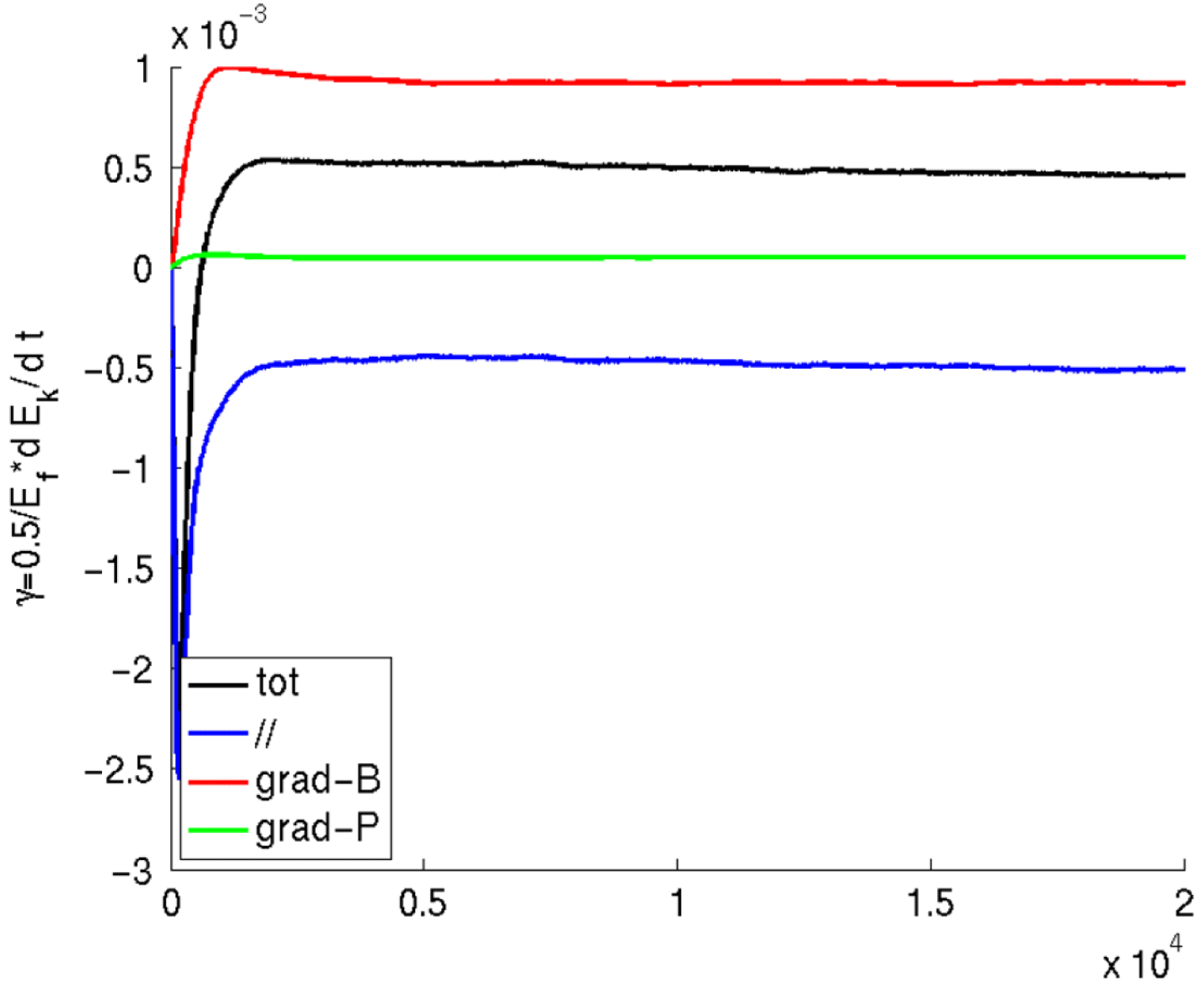
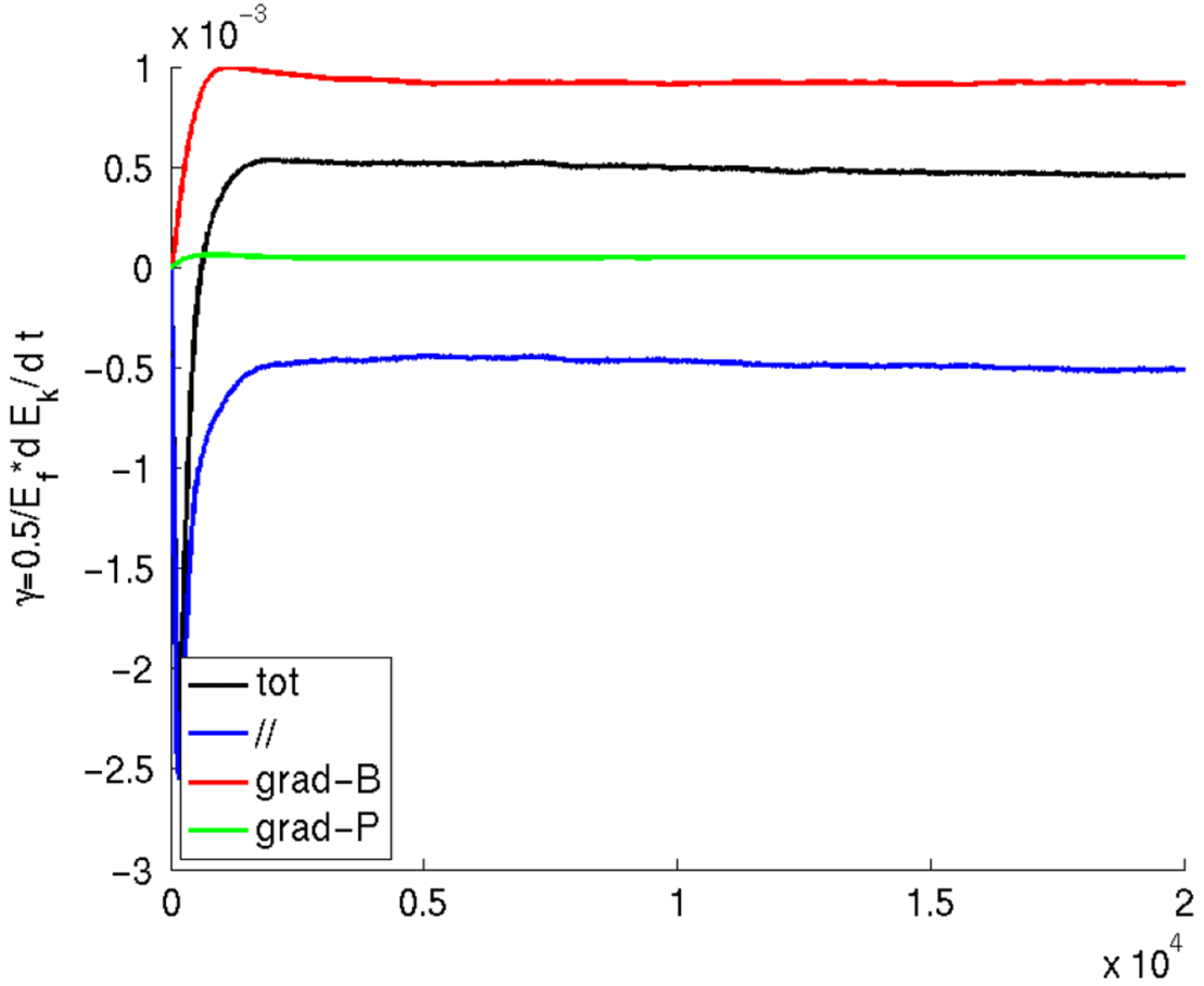
The different contributions to the growth rate arising from the different terms in the gyrocentre velocity can be easily separated in the power balance equation and give a clear indication of the kind of instabilities present in the system in both linear and nonlinear simulations:
The gyrokinetic field theory approach to the derivation of the GK equations leads naturally to the known result on energetic consistency: the same Hamiltonian must be used to construct the polarisation equation and the gyrokinetic Vlasov equations. All the approximations are done in the Lagrangian
![]() $L$
(hence
$L$
(hence
![]() $H$
) and then the equations are derived without any further approximation or additional ordering. This also implies that the approximations made cannot be relaxed once the equations have been derived. For example, as already discussed, the linearised polarisation equation has been obtained by considering only
$H$
) and then the equations are derived without any further approximation or additional ordering. This also implies that the approximations made cannot be relaxed once the equations have been derived. For example, as already discussed, the linearised polarisation equation has been obtained by considering only
![]() $fH=f(H_{0}+H_{1})$
while the term
$fH=f(H_{0}+H_{1})$
while the term
![]() $fH_{2}$
was replaced by
$fH_{2}$
was replaced by
![]() $f_{M}H_{2}$
; as a result, only
$f_{M}H_{2}$
; as a result, only
![]() $H_{0}+H_{1}$
contributed to the Euler–Lagrange particle motion equations. Therefore, if we want to construct a model with nonlinear polarisation, second-order terms in the fields, related to
$H_{0}+H_{1}$
contributed to the Euler–Lagrange particle motion equations. Therefore, if we want to construct a model with nonlinear polarisation, second-order terms in the fields, related to
![]() $H_{2}\,f$
, must be included in the equations of motion. On the other hand, if we want to extend the model by including second-order terms in the equations of motion, a nonlinear polarisation equation has to be used. A more detailed discussion of this topic can be found in Sugama (Reference Sugama2000) and Scott & Smirnov (Reference Scott and Smirnov2010).
$H_{2}\,f$
, must be included in the equations of motion. On the other hand, if we want to extend the model by including second-order terms in the equations of motion, a nonlinear polarisation equation has to be used. A more detailed discussion of this topic can be found in Sugama (Reference Sugama2000) and Scott & Smirnov (Reference Scott and Smirnov2010).
2.3. Adiabatic electrons
The electron contribution to the polarisation equation is often further approximated by replacing the electron density with a fluid approximation for the electron species. Using a fluid model for the electron motion, the equation for the parallel electron momentum, at the lowest order, is
We suppose that electrons react instantaneously to the electrostatic potential; therefore, the inertial term in the previous equation can be neglected: this is equivalent to imposing
![]() $m_{e}\rightarrow 0$
. The general solution of (2.69), for vanishing
$m_{e}\rightarrow 0$
. The general solution of (2.69), for vanishing
![]() $m_{e}$
, is
$m_{e}$
, is
In this model, known as the adiabatic electron approximation, the electron density is therefore proportional to the electrostatic potential. The value of the free function
![]() $F$
must be fixed by additional constraints. The equilibrium configuration of a magnetically confined plasma consists in general of a sequence of nested magnetic surfaces or flux surfaces. Almost every flux surface is covered ergodically by a single field line. In the case of electrostatic waves in a plasma with well-defined magnetic flux surfaces, there is no net radial transport of particles if the electrons are exactly adiabatic, since the radial particle flux vanishes when averaged over a flux surface (Dorland Reference Dorland1983). As a result, the total number of electrons on each flux surface must be conserved. Following the derivation proposed by Dorland (Reference Dorland1983), this constraint can be used to fix the value of the integration constant in (2.70) for magnetic configurations with well-defined flux surfaces (without magnetic islands). This can be achieved by taking the flux-surface average of (2.70):
$F$
must be fixed by additional constraints. The equilibrium configuration of a magnetically confined plasma consists in general of a sequence of nested magnetic surfaces or flux surfaces. Almost every flux surface is covered ergodically by a single field line. In the case of electrostatic waves in a plasma with well-defined magnetic flux surfaces, there is no net radial transport of particles if the electrons are exactly adiabatic, since the radial particle flux vanishes when averaged over a flux surface (Dorland Reference Dorland1983). As a result, the total number of electrons on each flux surface must be conserved. Following the derivation proposed by Dorland (Reference Dorland1983), this constraint can be used to fix the value of the integration constant in (2.70) for magnetic configurations with well-defined flux surfaces (without magnetic islands). This can be achieved by taking the flux-surface average of (2.70):
having introduced the flux-surface average operator
![]() $\langle \,\rangle$
and the flux-surface averaged density,
$\langle \,\rangle$
and the flux-surface averaged density,
![]() $\bar{n}_{e}(s,t)=\langle n_{e}(\boldsymbol{R},t)\rangle$
, where the flux-surface label
$\bar{n}_{e}(s,t)=\langle n_{e}(\boldsymbol{R},t)\rangle$
, where the flux-surface label
![]() $s$
plays the role of a radial coordinate. A detailed description of the flux-surface average operator in tokamaks can be found in Hinton & Hazeltine (Reference Hinton and Hazeltine1976). The condition of conservation of the number of electrons on each flux surface is
$s$
plays the role of a radial coordinate. A detailed description of the flux-surface average operator in tokamaks can be found in Hinton & Hazeltine (Reference Hinton and Hazeltine1976). The condition of conservation of the number of electrons on each flux surface is
![]() $\bar{n}_{e}(s,t)=n_{e0}(s)$
, leading to
$\bar{n}_{e}(s,t)=n_{e0}(s)$
, leading to
where
![]() $\bar{{\it\Phi}}(s,t)=\langle {\it\Phi}(\boldsymbol{R},t)\rangle$
is the electrostatic flux-surface averaged potential. Finally, the linearised quasi-neutrality equation for adiabatic electrons is
$\bar{{\it\Phi}}(s,t)=\langle {\it\Phi}(\boldsymbol{R},t)\rangle$
is the electrostatic flux-surface averaged potential. Finally, the linearised quasi-neutrality equation for adiabatic electrons is
where
![]() $\bar{{\it\Phi}}$
is the flux-surface averaged electrostatic potential. Although here the adiabatic electron approximation was not done in the Lagrangian, it is possible to show that the resulting set of equations can also be obtained via a Lagrangian formulation as described in Scott & Smirnov (Reference Scott and Smirnov2010). The adiabatic electron approximation largely reduces the difficulty and the numerical cost of gyrokinetic simulations. However, non-adiabatic electron effects, in particular the trapped electron dynamics, play an important role in experimentally relevant plasmas.
$\bar{{\it\Phi}}$
is the flux-surface averaged electrostatic potential. Although here the adiabatic electron approximation was not done in the Lagrangian, it is possible to show that the resulting set of equations can also be obtained via a Lagrangian formulation as described in Scott & Smirnov (Reference Scott and Smirnov2010). The adiabatic electron approximation largely reduces the difficulty and the numerical cost of gyrokinetic simulations. However, non-adiabatic electron effects, in particular the trapped electron dynamics, play an important role in experimentally relevant plasmas.
3. Particle-in-cell (PIC) discretisation
Different numerical methods can be used to solve the set of GK equations. One of the most common is the Lagrangian approach, based on a Monte Carlo algorithm in which a finite collection of initial positions in phase space is sampled by a set of particles, often called markers. This is the loading step in a PIC algorithm. Euler–Lagrange equations are solved to follow marker orbits in 5D, which is called pushing. On the other hand, the fields are solved on a grid. To this aim the source terms for the field equations at every time step need to be computed on the fixed grid by a procedure called charge and current assignment. Field equations are then solved on the same (3D) grid by means of finite-difference or finite-element methods, thus providing the electric field on the fixed grid. Interpolation techniques can then be used to get the value of the electric field at the marker positions. The Lagrangian approach is often referred to as PIC. The PIC method for standard plasma physics applications is described in the textbooks Hockney & Eastwood (Reference Hockney and Eastwood1988) and Birdsall & Langdon (Reference Birdsall and Langdon2004). It was introduced very early in the context of gyrokinetics by Lee (Reference Lee1983).
Let us now explain how the PIC method fits in the framework of Monte Carlo simulations and how the literature on this subject can be used to understand and improve PIC simulations. Good introductory textbooks on Monte Carlo simulations are Liu (Reference Liu2008) and Dunn & Shultis (Reference Dunn and Shultis2012). A discussion of the role of Monte Carlo sampling in gyrokinetic PIC methods can also be found in a review paper by Krommes (Reference Krommes2007).
3.1. Monte Carlo simulation
The principle of a Monte Carlo simulation is to approximate the expected value of a random variable by an average over a large number of samples. For our purposes a random variable
![]() $X$
is a function that can take values in
$X$
is a function that can take values in
![]() $\mathbb{R}$
(or
$\mathbb{R}$
(or
![]() $\mathbb{R}^{n}$
for a vector-valued random variable), which are distributed according to a probability density function. The random number generator available in numerical computation software typically generates a pseudo-random sequence uniformly distributed in
$\mathbb{R}^{n}$
for a vector-valued random variable), which are distributed according to a probability density function. The random number generator available in numerical computation software typically generates a pseudo-random sequence uniformly distributed in
![]() $[0,1]$
, which corresponds to the uniform probability density
$[0,1]$
, which corresponds to the uniform probability density
![]() $f=1$
. From this there are several techniques that enable one to generate samples of random variables that are distributed according to any density
$f=1$
. From this there are several techniques that enable one to generate samples of random variables that are distributed according to any density
![]() $f$
. In a PIC simulation, the probability density that will be used to generate samples will be the initial distribution of the particles
$f$
. In a PIC simulation, the probability density that will be used to generate samples will be the initial distribution of the particles
![]() $f_{0}$
, normalised to one so that it becomes a probability density. This procedure is called marker loading in the PIC literature, and consist in generating an initial particle distribution in phase space. In this case the random variable
$f_{0}$
, normalised to one so that it becomes a probability density. This procedure is called marker loading in the PIC literature, and consist in generating an initial particle distribution in phase space. In this case the random variable
![]() $Z$
is the phase-space position of a marker, which is distributed according to the initial particle phase-space density
$Z$
is the phase-space position of a marker, which is distributed according to the initial particle phase-space density
![]() $f_{0}$
. Each marker can then be seen as one realisation (i.e. one random draw) of the random variable
$f_{0}$
. Each marker can then be seen as one realisation (i.e. one random draw) of the random variable
![]() $Z$
. Another point of view, which is more convenient for the Monte Carlo theory, is to consider only one realisation for each of
$Z$
. Another point of view, which is more convenient for the Monte Carlo theory, is to consider only one realisation for each of
![]() $N$
random variables
$N$
random variables
![]() $Z_{i}$
which are identically distributed, i.e. which are drawn according to the same probability density. With both interpretations, we get at the end a sample of
$Z_{i}$
which are identically distributed, i.e. which are drawn according to the same probability density. With both interpretations, we get at the end a sample of
![]() $N$
independent markers that can be used to represent the probability density
$N$
independent markers that can be used to represent the probability density
![]() $f_{0}$
.
$f_{0}$
.
Once a random variable
![]() $X$
of the probability density function
$X$
of the probability density function
![]() $f$
is available, in our case the phase-space positions of the markers, arbitrary smooth functions
$f$
is available, in our case the phase-space positions of the markers, arbitrary smooth functions
![]() ${\it\psi}$
of these define new random variables, and we can compute expected values of these using the definition
${\it\psi}$
of these define new random variables, and we can compute expected values of these using the definition
We refer to Dunn & Shultis (Reference Dunn and Shultis2012) for a more detailed background on the probability terminology for Monte Carlo simulations, explaining in particular also the important notion of independence of random variables.
Now, the Monte Carlo method simply consists in approximating the expected value of some random variables by a sample average. To approximate
![]() $\mathbb{E}({\it\psi}(X))$
, we consider a sequence of independent random variables
$\mathbb{E}({\it\psi}(X))$
, we consider a sequence of independent random variables
![]() $(X_{i})_{i}$
distributed like
$(X_{i})_{i}$
distributed like
![]() $X$
and approximate
$X$
and approximate
![]() $\mathbb{E}({\it\psi}(X))$
by the sample mean
$\mathbb{E}({\it\psi}(X))$
by the sample mean
In order for this procedure to be useful, we need to check that the approximation we defined converges in some sense to the exact value and possibly estimate the speed of convergence.
Here the sample mean is an example of what is called an estimator in statistics, which is a rule for computing some statistical quantity, which is a function of the random variable, here the expected value, from sample data.
Definition 1. The difference between the expected value of the estimator and the statistical quantity it approximates is called bias. If this difference is zero, the estimator is said to be unbiased.
Let us compute the bias of the sample mean given by (3.2). We easily get as the
![]() $X_{i}$
are all distributed like
$X_{i}$
are all distributed like
![]() $X$
and thus have the same expected value that
$X$
and thus have the same expected value that
so that the bias is zero and our sample mean is unbiased.
Useful statistical quantities in Monte Carlo simulations are variance and covariance, which are defined as follows.
Definition 2. Let
![]() $X$
and
$X$
and
![]() $Y$
be two square integrable real valued random variables. The variance of the random variable
$Y$
be two square integrable real valued random variables. The variance of the random variable
![]() $X$
is defined by
$X$
is defined by
and
is called the standard deviation of the random variable
![]() $X$
. The covariance of
$X$
. The covariance of
![]() $X$
and
$X$
and
![]() $Y$
is defined by
$Y$
is defined by
We have obviously that
![]() $\mathbb{V}(X)=\text{Cov}(X,X)$
. The variance can also be expressed by
$\mathbb{V}(X)=\text{Cov}(X,X)$
. The variance can also be expressed by
![]() $\mathbb{V}(X)=\mathbb{E}(|X|^{2})-\mathbb{E}(X)^{2}$
. Indeed, this follows from a simple computation, relying on the linearity of the expected value, which is an integral, and as
$\mathbb{V}(X)=\mathbb{E}(|X|^{2})-\mathbb{E}(X)^{2}$
. Indeed, this follows from a simple computation, relying on the linearity of the expected value, which is an integral, and as
![]() $a=\mathbb{E}(X)$
is a number we have, as
$a=\mathbb{E}(X)$
is a number we have, as
![]() $f$
is a probability density which integrates to one,
$f$
is a probability density which integrates to one,
In the same way,
A useful result is Bienaymé’s equality, as follows.
Theorem 1 (Bienaymé).
If
![]() $X_{1},\dots ,X_{m}$
are independent real valued random variables with
$X_{1},\dots ,X_{m}$
are independent real valued random variables with
![]() $\mathbb{V}(|X_{i}|)<+\infty$
, then
$\mathbb{V}(|X_{i}|)<+\infty$
, then
Assuming that the sample number
![]() $N\geqslant 2$
, an unbiased estimator of the variance is given by the following sample variance:
$N\geqslant 2$
, an unbiased estimator of the variance is given by the following sample variance:
Indeed, let us compute the expected value of
![]() $V_{N}$
. Denoting
$V_{N}$
. Denoting
![]() $a=\mathbb{E}(X_{i})$
for
$a=\mathbb{E}(X_{i})$
for
![]() $i=1,\dots ,N$
, we have
$i=1,\dots ,N$
, we have
as
![]() $2\sum _{i=1}^{N}(X_{i}-a)(a-M_{N})=-2N(M_{N}-a)^{2}$
. Hence,
$2\sum _{i=1}^{N}(X_{i}-a)(a-M_{N})=-2N(M_{N}-a)^{2}$
. Hence,
 $$\begin{eqnarray}\displaystyle \mathbb{E}(V_{N}) & = & \displaystyle \frac{1}{N-1}\mathop{\sum }_{i=1}^{N}\mathbb{E}((X_{i}-a)^{2})-\frac{N}{N-1}\mathbb{E}((M_{N}-a)^{2})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{N-1}\mathop{\sum }_{i=1}^{N}\mathbb{V}(X_{i})-\frac{N}{N-1}\mathbb{V}(M_{N}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}(V_{N}) & = & \displaystyle \frac{1}{N-1}\mathop{\sum }_{i=1}^{N}\mathbb{E}((X_{i}-a)^{2})-\frac{N}{N-1}\mathbb{E}((M_{N}-a)^{2})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{N-1}\mathop{\sum }_{i=1}^{N}\mathbb{V}(X_{i})-\frac{N}{N-1}\mathbb{V}(M_{N}).\end{eqnarray}$$
And, because of Bienaymé’s theorem,
Hence,
Remark 1. Note the
![]() $1/(N-1)$
factor in the variance estimator instead of the
$1/(N-1)$
factor in the variance estimator instead of the
![]() $1/N$
that one would expect at first glance. Using
$1/N$
that one would expect at first glance. Using
![]() $1/N$
instead would also yield an estimator of the variance, but this one would be biased, i.e. it would not have the correct expected value.
$1/N$
instead would also yield an estimator of the variance, but this one would be biased, i.e. it would not have the correct expected value.
3.2. Estimation of the error in a Monte Carlo simulation
Let us first compute in a general way the mean square error (MSE) of an estimator. Assume that
![]() $\hat{{\it\theta}}$
is an estimator for the statistical quantity
$\hat{{\it\theta}}$
is an estimator for the statistical quantity
![]() ${\it\theta}$
which is a real number that can be computed as a function of a random variable
${\it\theta}$
which is a real number that can be computed as a function of a random variable
![]() $X$
. The MSE is defined by
$X$
. The MSE is defined by
Note that the root mean square error or RMS error, which is the square root of the MSE, is the classical
![]() $L^{2}$
error.
$L^{2}$
error.
Lemma 1. Assume that the random variable
![]() $\hat{{\it\theta}}$
is an estimator for
$\hat{{\it\theta}}$
is an estimator for
![]() ${\it\theta}$
and
${\it\theta}$
and
![]() $\mathbb{E}(\hat{{\it\theta}}^{2})<+\infty$
. Then
$\mathbb{E}(\hat{{\it\theta}}^{2})<+\infty$
. Then
Proof. A straightforward calculation yields
 $$\begin{eqnarray}\displaystyle \text{MSE}(\hat{{\it\theta}}) & = & \displaystyle \mathbb{E}((\hat{{\it\theta}}-{\it\theta})^{2})=\mathbb{E}(\hat{{\it\theta}}^{2})+{\it\theta}^{2}-2{\it\theta}\mathbb{E}(\hat{{\it\theta}})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(\hat{{\it\theta}}^{2})-\mathbb{E}(\hat{{\it\theta}})^{2}+\mathbb{E}(\hat{{\it\theta}})^{2}+{\it\theta}^{2}-2{\it\theta}\mathbb{E}(\hat{{\it\theta}})\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{E}(\hat{{\it\theta}}^{2})-\mathbb{E}(\hat{{\it\theta}})^{2})+(\mathbb{E}(\hat{{\it\theta}})-{\it\theta})^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{V}(\hat{{\it\theta}})+(\text{Bias}(\hat{{\it\theta}}))^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{MSE}(\hat{{\it\theta}}) & = & \displaystyle \mathbb{E}((\hat{{\it\theta}}-{\it\theta})^{2})=\mathbb{E}(\hat{{\it\theta}}^{2})+{\it\theta}^{2}-2{\it\theta}\mathbb{E}(\hat{{\it\theta}})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(\hat{{\it\theta}}^{2})-\mathbb{E}(\hat{{\it\theta}})^{2}+\mathbb{E}(\hat{{\it\theta}})^{2}+{\it\theta}^{2}-2{\it\theta}\mathbb{E}(\hat{{\it\theta}})\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{E}(\hat{{\it\theta}}^{2})-\mathbb{E}(\hat{{\it\theta}})^{2})+(\mathbb{E}(\hat{{\it\theta}})-{\it\theta})^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{V}(\hat{{\it\theta}})+(\text{Bias}(\hat{{\it\theta}}))^{2}.\end{eqnarray}$$
Assume that the random variable
![]() $X$
defining our Monte Carlo simulation verifies
$X$
defining our Monte Carlo simulation verifies
![]() $\mathbb{E}(X^{2})<+\infty$
. Then we can apply the previous lemma to
$\mathbb{E}(X^{2})<+\infty$
. Then we can apply the previous lemma to
![]() $M_{N}$
as an estimator of
$M_{N}$
as an estimator of
![]() $\mathbb{E}(X)$
, which yields
$\mathbb{E}(X)$
, which yields
So, the RMS error is composed of two parts, the error coming from the variance of the sample and the possible bias on the sample occurring when the expected value of
![]() $M_{N}$
is not exactly equal to the expected value of the random variable
$M_{N}$
is not exactly equal to the expected value of the random variable
![]() $X$
being approximated.
$X$
being approximated.
In many cases the bias can be made to be zero, but in some cases it can be useful to introduce some bias in order to decrease the variance of the sample and the total error.
Lemma 2. Assume that
![]() $\mathbb{E}(X^{2})<+\infty$
. Then the RMS error for an unbiased simulation based on the random variable
$\mathbb{E}(X^{2})<+\infty$
. Then the RMS error for an unbiased simulation based on the random variable
![]() $X$
is
$X$
is
Proof. The formula (3.16) giving the mean squared error of an estimator shows that if the simulation is unbiased,
![]() $\mathbb{E}(M_{N})=\mathbb{E}(X)$
and
$\mathbb{E}(M_{N})=\mathbb{E}(X)$
and
Now, using Bienaymé’s theorem, we also have
Thus,
![]() $\mathbb{V}(M_{N})=\mathbb{V}(X)/N$
, which gives the result.
$\mathbb{V}(M_{N})=\mathbb{V}(X)/N$
, which gives the result.
The law of large numbers, strong or weak, implies that the sample mean converges towards the desired expected value, which justifies the Monte Carlo method.
Another major theorem of probability theory, the central limit theorem, gives a precise estimation of the error committed by an approximation.
Theorem 2 (Central limit theorem).
Assume that
![]() $(X_{1},X_{2},\dots ,X_{N})$
is a sequence of independent identically distributed random variables such that
$(X_{1},X_{2},\dots ,X_{N})$
is a sequence of independent identically distributed random variables such that
![]() $\mathbb{V}(X)={\it\sigma}^{2}(X)<\infty$
. Then
$\mathbb{V}(X)={\it\sigma}^{2}(X)<\infty$
. Then
This tells us that the asymptotic distribution of
![]() $(M_{N}-\mathbb{E}(X))/({\it\sigma}(X)/\sqrt{N})$
is a unit normal distribution or, equivalently, that
$(M_{N}-\mathbb{E}(X))/({\it\sigma}(X)/\sqrt{N})$
is a unit normal distribution or, equivalently, that
![]() $M_{N}$
is a normal distribution with mean
$M_{N}$
is a normal distribution with mean
![]() $\mathbb{E}(X)$
and standard deviation
$\mathbb{E}(X)$
and standard deviation
![]() ${\it\sigma}(X)/\sqrt{N}$
.
${\it\sigma}(X)/\sqrt{N}$
.
The right-hand side of (3.22) is a number that can be computed explicitly, and that is called the confidence coefficient. For
![]() ${\it\lambda}=3$
, the confidence coefficient is 0.9973 and for
${\it\lambda}=3$
, the confidence coefficient is 0.9973 and for
![]() ${\it\lambda}=4$
the confidence coefficient is 0.9999 (see e.g. Dunn & Shultis Reference Dunn and Shultis2012 for other values). This is the probability that the true mean lies in the so-called confidence interval
${\it\lambda}=4$
the confidence coefficient is 0.9999 (see e.g. Dunn & Shultis Reference Dunn and Shultis2012 for other values). This is the probability that the true mean lies in the so-called confidence interval
![]() $[M_{N}-{\it\lambda}{\it\sigma}(X)/\sqrt{N},M_{N}+{\it\lambda}{\it\sigma}(X)/\sqrt{N}]$
. Note that deterministic error estimates are generally of the form
$[M_{N}-{\it\lambda}{\it\sigma}(X)/\sqrt{N},M_{N}+{\it\lambda}{\it\sigma}(X)/\sqrt{N}]$
. Note that deterministic error estimates are generally of the form
![]() $h^{p}$
or
$h^{p}$
or
![]() $1/N^{p}$
, where
$1/N^{p}$
, where
![]() $h$
is a cell size and
$h$
is a cell size and
![]() $N$
a number of discretisation points, and lie on a deterministic curve. As an opposite to this, the error estimate in a Monte Carlo method is random, but it is always a normal distribution with variance which tends to 0 when the number of sample points tends to
$N$
a number of discretisation points, and lie on a deterministic curve. As an opposite to this, the error estimate in a Monte Carlo method is random, but it is always a normal distribution with variance which tends to 0 when the number of sample points tends to
![]() $+\infty$
. In practice a good estimate of the error is given by
$+\infty$
. In practice a good estimate of the error is given by
![]() ${\it\sigma}(X)/\sqrt{N}$
, which is all the more interesting in that the variance (or standard deviation) can be well estimated by the sample variance (or sample standard deviation), which is an a posteriori estimate that can be directly used in actual computations to measure the error.
${\it\sigma}(X)/\sqrt{N}$
, which is all the more interesting in that the variance (or standard deviation) can be well estimated by the sample variance (or sample standard deviation), which is an a posteriori estimate that can be directly used in actual computations to measure the error.
3.3. The Monte Carlo PIC algorithm
We now derive the Monte Carlo PIC algorithm from a given Lagrangian as was first proposed by Lewis (Reference Lewis1970) and also more recently by Evstatiev & Shadwick (Reference Evstatiev and Shadwick2013). We consider a Lagrangian that is built using the single-particle Lagrangian for each particle species
![]() $L_{sp}$
and a field Lagrangian
$L_{sp}$
and a field Lagrangian
![]() $L_{F}$
:
$L_{F}$
:
Here
![]() $f_{sp}(\boldsymbol{Z}_{0},t_{0})$
denotes the initial phase-space density of species
$f_{sp}(\boldsymbol{Z}_{0},t_{0})$
denotes the initial phase-space density of species
![]() $\text{sp}$
and
$\text{sp}$
and
![]() $\boldsymbol{Z}(\boldsymbol{Z}_{0},t_{0};t)$
are the characteristics of the GK Vlasov equations, i.e. the particle phase-space trajectories, with initial condition
$\boldsymbol{Z}(\boldsymbol{Z}_{0},t_{0};t)$
are the characteristics of the GK Vlasov equations, i.e. the particle phase-space trajectories, with initial condition
![]() $\boldsymbol{Z}_{0}$
at time
$\boldsymbol{Z}_{0}$
at time
![]() $t_{0}$
. Using the Liouville theorem the Lagrangian can also be written as
$t_{0}$
. Using the Liouville theorem the Lagrangian can also be written as
We notice here that the particle contribution to the Lagrangian is written as a sum of integrals with densities
![]() $f_{sp}$
. Using the definition of expected values, each of them can be replaced by an expected value of a random variable
$f_{sp}$
. Using the definition of expected values, each of them can be replaced by an expected value of a random variable
![]() $\boldsymbol{Z}_{sp}(t)$
of probability density
$\boldsymbol{Z}_{sp}(t)$
of probability density
![]() $f_{sp}(\cdot ,t)$
. This yields
$f_{sp}(\cdot ,t)$
. This yields
The particle contribution of the Lagrangian now being expressed as an expected value, the Monte Carlo method can be applied by replacing the expected value by a sample mean over a large number of samples being drawn independently according to the initial distributions
![]() $f_{sp}(\cdot ,t_{0})$
, which yields the Monte Carlo Lagrangian
$f_{sp}(\cdot ,t_{0})$
, which yields the Monte Carlo Lagrangian
Even though it does not appear explicitly in our notation, the number of particles
![]() $N_{p}$
can be different for each species. We also remove the sp index from the marker positions to alleviate the notation.
$N_{p}$
can be different for each species. We also remove the sp index from the marker positions to alleviate the notation.
It now remains to discretise the fields. In the variational framework, the most natural method to do this is given by the Galerkin approximation, which consists in doing the variations over functions constrained to remain in a finite-dimensional function space. This then leads to a finite-element approximation of the fields. Introducing the basis functions
![]() ${\it\Lambda}_{{\it\nu}}$
of the finite-dimensional function space, all the functions in this space can be expressed as linear combinations of these basis functions:
${\it\Lambda}_{{\it\nu}}$
of the finite-dimensional function space, all the functions in this space can be expressed as linear combinations of these basis functions:
where
![]() ${\it\Phi}_{{\it\mu}}(t)$
are real numbers and
${\it\Phi}_{{\it\mu}}(t)$
are real numbers and
![]() ${\it\Lambda}_{{\it\mu}}(\boldsymbol{x})={\it\Lambda}_{j}(x_{1}){\it\Lambda}_{k}(x_{2}){\it\Lambda}_{l}(x_{3})$
is a product of polynomial basis functions, typically cubic B-splines. Replacing
${\it\Lambda}_{{\it\mu}}(\boldsymbol{x})={\it\Lambda}_{j}(x_{1}){\it\Lambda}_{k}(x_{2}){\it\Lambda}_{l}(x_{3})$
is a product of polynomial basis functions, typically cubic B-splines. Replacing
![]() ${\it\Phi}$
by
${\it\Phi}$
by
![]() ${\it\Phi}_{h}$
in the Lagrangian equation (2.18), we get the following finite-dimensional Lagrangian:
${\it\Phi}_{h}$
in the Lagrangian equation (2.18), we get the following finite-dimensional Lagrangian:
 $$\begin{eqnarray}\displaystyle L_{h,MC} & = & \displaystyle \mathop{\sum }_{sp}\frac{1}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}\left(\left(\frac{e}{c}\boldsymbol{A}(\boldsymbol{R}_{k})+p_{\Vert ,k}\boldsymbol{b}(\boldsymbol{R}_{k})\right)\boldsymbol{\cdot }\dot{\boldsymbol{R}}_{k}+\frac{mc}{e}{\it\mu}_{k}\dot{{\it\theta}}_{k}-m\frac{U^{2}}{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\vphantom{\left(\frac{e^{2}}{c_{3}}\right)}-\,{\it\mu}B(\boldsymbol{R}_{k})-e\text{J}_{0}{\it\Phi}_{h}(\boldsymbol{R}_{k})\right)+\mathop{\sum }_{sp}\int \text{d}{\it\Omega}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}_{h}|^{2}f_{M}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{h,MC} & = & \displaystyle \mathop{\sum }_{sp}\frac{1}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}\left(\left(\frac{e}{c}\boldsymbol{A}(\boldsymbol{R}_{k})+p_{\Vert ,k}\boldsymbol{b}(\boldsymbol{R}_{k})\right)\boldsymbol{\cdot }\dot{\boldsymbol{R}}_{k}+\frac{mc}{e}{\it\mu}_{k}\dot{{\it\theta}}_{k}-m\frac{U^{2}}{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\vphantom{\left(\frac{e^{2}}{c_{3}}\right)}-\,{\it\mu}B(\boldsymbol{R}_{k})-e\text{J}_{0}{\it\Phi}_{h}(\boldsymbol{R}_{k})\right)+\mathop{\sum }_{sp}\int \text{d}{\it\Omega}\frac{mc^{2}}{2B^{2}}|\boldsymbol{{\rm\nabla}}_{\bot }{\it\Phi}_{h}|^{2}f_{M}.\end{eqnarray}$$
Note that we have already here introduced an importance weight
![]() $w_{k}$
that we shall explain in the next section. For the moment we have
$w_{k}$
that we shall explain in the next section. For the moment we have
![]() $w_{k}=1$
for all
$w_{k}=1$
for all
![]() $k$
. We shall compute the Euler–Lagrange equations corresponding to this finite-dimensional Lagrangian after having introduced variance-reduction techniques, which are essential for gyrokinetic PIC computations.
$k$
. We shall compute the Euler–Lagrange equations corresponding to this finite-dimensional Lagrangian after having introduced variance-reduction techniques, which are essential for gyrokinetic PIC computations.
At this level no time discretisation has been performed. As the semi-discrete Lagrangian is still invariant with respect to a time translation, the corresponding Noether energy is exactly conserved. The equations of motion of the particles are discretised using a standard fourth-order Runge–Kutta procedure, which breaks the exact energy conservation. However, as will be discussed later, numerical simulations still exhibit in practice very good energy conservation properties.
3.4. Variance-reduction techniques
As we saw, the Monte Carlo error for the approximation of the expected value of a random variable
![]() $X$
is
$X$
is
![]() ${\it\sigma}(X)/\sqrt{N}$
. Apart from increasing the number of realisations
${\it\sigma}(X)/\sqrt{N}$
. Apart from increasing the number of realisations
![]() $N$
, the most efficient method to reduce the error is to use available information to replace
$N$
, the most efficient method to reduce the error is to use available information to replace
![]() $X$
by another random variable with the same expected value but a lower variance. We shall describe two techniques that are used for this purpose in the context of PIC methods.
$X$
by another random variable with the same expected value but a lower variance. We shall describe two techniques that are used for this purpose in the context of PIC methods.
3.4.1. Importance sampling
We are interested in computing, for some given probability density
![]() $f$
, quantities of the form
$f$
, quantities of the form
The standard Monte Carlo method for doing this is to define our integral as an expected value using a random variable
![]() $\boldsymbol{Z}$
of density
$\boldsymbol{Z}$
of density
![]() $f$
. Then
$f$
. Then
Depending on the function
![]() ${\it\psi}$
, it might not be the best approach to use directly the density
${\it\psi}$
, it might not be the best approach to use directly the density
![]() $f$
for drawing the random variable used in the simulation. Indeed, if
$f$
for drawing the random variable used in the simulation. Indeed, if
![]() $g$
is any other probability density that does not vanish in the support of
$g$
is any other probability density that does not vanish in the support of
![]() $f$
, one can express our integral as an expectation using a random variable
$f$
, one can express our integral as an expectation using a random variable
![]() $\tilde{\boldsymbol{Z}}$
of density
$\tilde{\boldsymbol{Z}}$
of density
![]() $g$
:
$g$
:
where the random variable
![]() $W(\tilde{\boldsymbol{Z}})=f(\tilde{\boldsymbol{Z}})/g(\tilde{\boldsymbol{Z}})$
is called weight.
$W(\tilde{\boldsymbol{Z}})=f(\tilde{\boldsymbol{Z}})/g(\tilde{\boldsymbol{Z}})$
is called weight.
The Monte Carlo approximation using independent random variables distributed identically with density
![]() $g$
can be expressed as
$g$
can be expressed as
from which we get
So,
![]() $\tilde{M}_{N}$
is another unbiased estimator of the integral we wish to compute and the approximation error for a given number of samples
$\tilde{M}_{N}$
is another unbiased estimator of the integral we wish to compute and the approximation error for a given number of samples
![]() $N$
is determined by its variance.
$N$
is determined by its variance.
Let us now investigate how
![]() $g$
can be chosen to get a smaller variance. For this, we need to compare the variance of
$g$
can be chosen to get a smaller variance. For this, we need to compare the variance of
![]() $W(\tilde{\boldsymbol{Z}}){\it\psi}(\tilde{\boldsymbol{Z}})$
and the variance of
$W(\tilde{\boldsymbol{Z}}){\it\psi}(\tilde{\boldsymbol{Z}})$
and the variance of
![]() ${\it\psi}(\boldsymbol{Z})$
knowing that both have the same expected value:
${\it\psi}(\boldsymbol{Z})$
knowing that both have the same expected value:
On the other hand,
So, we see that there is a factor
![]() $W$
difference between the two expressions and obviously if
$W$
difference between the two expressions and obviously if
![]() $W<1$
in regions where
$W<1$
in regions where
![]() ${\it\psi}$
is larger, the procedure will lead to a smaller variance. Note that because
${\it\psi}$
is larger, the procedure will lead to a smaller variance. Note that because
![]() $f$
and
$f$
and
![]() $g$
both have an integral one, we cannot have
$g$
both have an integral one, we cannot have
![]() $W<1$
everywhere.
$W<1$
everywhere.
We also remark that, assuming that
![]() ${\it\psi}(\boldsymbol{z})$
does not vanish, if we take
${\it\psi}(\boldsymbol{z})$
does not vanish, if we take
![]() $W(\boldsymbol{z})=\mathbb{E}({\it\psi}(\boldsymbol{Z}))/{\it\psi}(\boldsymbol{z})$
, which corresponds to
$W(\boldsymbol{z})=\mathbb{E}({\it\psi}(\boldsymbol{Z}))/{\it\psi}(\boldsymbol{z})$
, which corresponds to
![]() $g(\boldsymbol{z})=f(\boldsymbol{z}){\it\psi}(\boldsymbol{z})/\mathbb{E}({\it\psi}(\boldsymbol{Z}))$
, we get
$g(\boldsymbol{z})=f(\boldsymbol{z}){\it\psi}(\boldsymbol{z})/\mathbb{E}({\it\psi}(\boldsymbol{Z}))$
, we get
so that
![]() $\mathbb{V}(W(\tilde{\boldsymbol{Z}}){\it\psi}(\tilde{\boldsymbol{Z}}))=0$
. This of course cannot be done in practice as
$\mathbb{V}(W(\tilde{\boldsymbol{Z}}){\it\psi}(\tilde{\boldsymbol{Z}}))=0$
. This of course cannot be done in practice as
![]() $\mathbb{E}({\it\psi}(\boldsymbol{Z}))$
is the unknown quantity we wish to approximate, but it can be used as a guideline to find a density
$\mathbb{E}({\it\psi}(\boldsymbol{Z}))$
is the unknown quantity we wish to approximate, but it can be used as a guideline to find a density
![]() $g$
that reduces the variance as much as possible and tells us that the density
$g$
that reduces the variance as much as possible and tells us that the density
![]() $g$
should be proportional to the integrand
$g$
should be proportional to the integrand
![]() $f{\it\psi}$
, i.e. that markers should be distributed according to the integrand.
$f{\it\psi}$
, i.e. that markers should be distributed according to the integrand.
3.4.2. Control variates
Consider the standard Monte Carlo problem of approximating
![]() $a=\mathbb{E}(X)$
, for a given random variable
$a=\mathbb{E}(X)$
, for a given random variable
![]() $X$
, by a sample mean.
$X$
, by a sample mean.
Assume now that there exists a random variable
![]() $Y$
the expected value of which is known, that is somehow correlated to
$Y$
the expected value of which is known, that is somehow correlated to
![]() $X$
. For a given
$X$
. For a given
![]() ${\it\alpha}\in \mathbb{R}$
, let us define the new random variable
${\it\alpha}\in \mathbb{R}$
, let us define the new random variable
Obviously, we have for any
![]() ${\it\alpha}$
that
${\it\alpha}$
that
![]() $\mathbb{E}(Z_{{\it\alpha}})=\mathbb{E}(X)=a$
, which means that the sample mean of
$\mathbb{E}(Z_{{\it\alpha}})=\mathbb{E}(X)=a$
, which means that the sample mean of
![]() $Z_{{\it\alpha}}$
,
$Z_{{\it\alpha}}$
,
could be used instead of the sample mean of
![]() $X$
to approximate
$X$
to approximate
![]() $a$
. The random variable
$a$
. The random variable
![]() ${\it\alpha}Y$
is called a control variate for
${\it\alpha}Y$
is called a control variate for
![]() $X$
.
$X$
.
Let us now look under what conditions the variance of
![]() $Z_{{\it\alpha}}$
is lower than the variance of
$Z_{{\it\alpha}}$
is lower than the variance of
![]() $X$
. We assume that both
$X$
. We assume that both
![]() $\mathbb{V}(X)>0$
and
$\mathbb{V}(X)>0$
and
![]() $\mathbb{V}(Y)>0$
.
$\mathbb{V}(Y)>0$
.
Lemma 3. If the random variables
![]() $X$
and
$X$
and
![]() $Y$
are not independent, there exists a value of
$Y$
are not independent, there exists a value of
![]() ${\it\alpha}$
for which the variance of
${\it\alpha}$
for which the variance of
![]() $Z_{{\it\alpha}}$
is smaller than the variance of
$Z_{{\it\alpha}}$
is smaller than the variance of
![]() $X$
. More precisely,
$X$
. More precisely,
Moreover,
Proof. As
![]() $Z_{{\it\alpha}}=X-{\it\alpha}Y+{\it\alpha}\mathbb{E}(Y)$
and
$Z_{{\it\alpha}}=X-{\it\alpha}Y+{\it\alpha}\mathbb{E}(Y)$
and
![]() $\mathbb{E}(Z_{{\it\alpha}})=\mathbb{E}(X)$
, we have
$\mathbb{E}(Z_{{\it\alpha}})=\mathbb{E}(X)$
, we have
 $$\begin{eqnarray}\displaystyle \mathbb{V}(Z_{{\it\alpha}}) & = & \displaystyle \mathbb{E}(Z_{{\it\alpha}}^{2})-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}((X-{\it\alpha}Y)^{2})+2{\it\alpha}\mathbb{E}(Y)\mathbb{E}(X-{\it\alpha}Y)+{\it\alpha}^{2}\mathbb{E}(Y)^{2}-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(X^{2})-2{\it\alpha}\mathbb{E}(XY)+{\it\alpha}^{2}\mathbb{E}(Y^{2})+2{\it\alpha}\mathbb{E}(Y)\mathbb{E}(X)\nonumber\\ \displaystyle & & \displaystyle -\,2{\it\alpha}^{2}\mathbb{E}(Y)^{2}+{\it\alpha}^{2}\mathbb{E}(Y)^{2}-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{V}(X)-2{\it\alpha}\text{Cov}(X,Y)+{\it\alpha}^{2}\mathbb{V}(Y)\nonumber\\ \displaystyle & = & \displaystyle {\it\sigma}^{2}(X)-2{\it\alpha}{\it\sigma}(X){\it\sigma}(Y){\it\rho}(X,Y)+{\it\alpha}^{2}{\it\sigma}^{2}(Y),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{V}(Z_{{\it\alpha}}) & = & \displaystyle \mathbb{E}(Z_{{\it\alpha}}^{2})-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}((X-{\it\alpha}Y)^{2})+2{\it\alpha}\mathbb{E}(Y)\mathbb{E}(X-{\it\alpha}Y)+{\it\alpha}^{2}\mathbb{E}(Y)^{2}-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(X^{2})-2{\it\alpha}\mathbb{E}(XY)+{\it\alpha}^{2}\mathbb{E}(Y^{2})+2{\it\alpha}\mathbb{E}(Y)\mathbb{E}(X)\nonumber\\ \displaystyle & & \displaystyle -\,2{\it\alpha}^{2}\mathbb{E}(Y)^{2}+{\it\alpha}^{2}\mathbb{E}(Y)^{2}-\mathbb{E}(X)^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{V}(X)-2{\it\alpha}\text{Cov}(X,Y)+{\it\alpha}^{2}\mathbb{V}(Y)\nonumber\\ \displaystyle & = & \displaystyle {\it\sigma}^{2}(X)-2{\it\alpha}{\it\sigma}(X){\it\sigma}(Y){\it\rho}(X,Y)+{\it\alpha}^{2}{\it\sigma}^{2}(Y),\end{eqnarray}$$
introducing the standard deviation of a random variable
![]() ${\it\sigma}^{2}(X)=\mathbb{V}(X)$
and the correlation coefficient of two random variables
${\it\sigma}^{2}(X)=\mathbb{V}(X)$
and the correlation coefficient of two random variables
![]() ${\it\rho}(X,Y)=\text{Cov}(X,Y)/({\it\sigma}(X){\it\sigma}(Y))$
.
${\it\rho}(X,Y)=\text{Cov}(X,Y)/({\it\sigma}(X){\it\sigma}(Y))$
.
So, the variance of
![]() $Z_{{\it\alpha}}$
is a second-order polynomial in
$Z_{{\it\alpha}}$
is a second-order polynomial in
![]() ${\it\alpha}$
the minimum of which is reached for
${\it\alpha}$
the minimum of which is reached for
and, inserting this into the expression of
![]() $\mathbb{V}(Z_{{\it\alpha}})$
, we get
$\mathbb{V}(Z_{{\it\alpha}})$
, we get
On the other hand,
Hence, for
![]() ${\it\alpha}>0$
,
${\it\alpha}>0$
,
and, for
![]() ${\it\alpha}<0$
,
${\it\alpha}<0$
,
![]() $\mathbb{V}(Z_{{\it\alpha}})<\mathbb{V}(X)\Leftrightarrow {\it\alpha}>2{\it\alpha}^{\ast }$
.
$\mathbb{V}(Z_{{\it\alpha}})<\mathbb{V}(X)\Leftrightarrow {\it\alpha}>2{\it\alpha}^{\ast }$
.
Remark 2. This result means that provided that
![]() $\text{Cov}(X,Y)\neq 0$
, i.e.
$\text{Cov}(X,Y)\neq 0$
, i.e.
![]() $X$
and
$X$
and
![]() $Y$
are not independent, there is always an interval around the optimal value
$Y$
are not independent, there is always an interval around the optimal value
![]() ${\it\alpha}^{\ast }$
for which
${\it\alpha}^{\ast }$
for which
![]() $Z_{{\it\alpha}}$
has a lower variance than
$Z_{{\it\alpha}}$
has a lower variance than
![]() $X$
. The more correlated
$X$
. The more correlated
![]() $X$
and
$X$
and
![]() $Y$
are, the larger this interval is. So, the most important thing is to find a random variable
$Y$
are, the larger this interval is. So, the most important thing is to find a random variable
![]() $Y$
the expectation of which is known, that is as correlated with
$Y$
the expectation of which is known, that is as correlated with
![]() $X$
as possible. Then, if a good approximation of
$X$
as possible. Then, if a good approximation of
![]() $\text{Cov}(X,Y)$
can be computed, one can use this to get closer to
$\text{Cov}(X,Y)$
can be computed, one can use this to get closer to
![]() ${\it\alpha}^{\ast }$
and minimise the variance as much as possible with the random variable
${\it\alpha}^{\ast }$
and minimise the variance as much as possible with the random variable
![]() $Y$
.
$Y$
.
A typical example is when
![]() $X=Y+{\it\epsilon}{\tilde{Y}}$
, where
$X=Y+{\it\epsilon}{\tilde{Y}}$
, where
![]() ${\it\epsilon}$
is small and
${\it\epsilon}$
is small and
![]() $\mathbb{E}(Y)$
is known and for simplicity
$\mathbb{E}(Y)$
is known and for simplicity
![]() $Y$
and
$Y$
and
![]() ${\tilde{Y}}$
are independent. Inserting this in the expression of
${\tilde{Y}}$
are independent. Inserting this in the expression of
![]() $\mathbb{V}(Z_{{\it\alpha}})$
in the above proof yields
$\mathbb{V}(Z_{{\it\alpha}})$
in the above proof yields
so that taking
![]() ${\it\alpha}=1$
yields that
${\it\alpha}=1$
yields that
![]() $\mathbb{V}(Z_{{\it\alpha}})$
is of order
$\mathbb{V}(Z_{{\it\alpha}})$
is of order
![]() ${\it\epsilon}^{2}$
assuming that
${\it\epsilon}^{2}$
assuming that
![]() $\mathbb{V}({\tilde{Y}})$
is of order 1. This is typically the form that is used in PIC simulations.
$\mathbb{V}({\tilde{Y}})$
is of order 1. This is typically the form that is used in PIC simulations.
3.5. Application of the variance-reduction techniques to the PIC method
For the PIC method, we can combine the importance-sampling method and the control variates method.
3.5.1. Importance sampling
The choice of a density for importance sampling depends on the expected value that we are interested in. There are many of those in a PIC code, but arguably the accurate computation of the electromagnetic field, which determines the self-consistent dynamics, is the most important. Depending on the physical problem we want to deal with more particles will be needed in some specific phase-space areas, like for example in some region of the tail for a bump-on-tail instability. For this reason, it is interesting in a PIC code to have the flexibility of drawing the particles according to any density, but one needs to be careful with the choice of this density as the results can become better or worse.
Initialisation. Assume that we know the density
![]() $g_{0}$
according to which we want to draw the markers. Then we initialise the markers’ phase-space positions
$g_{0}$
according to which we want to draw the markers. Then we initialise the markers’ phase-space positions
![]() $\boldsymbol{z}_{i}^{0}=(\boldsymbol{x}_{i}^{0},\boldsymbol{v}_{i}^{0})$
as realisations of a random variable
$\boldsymbol{z}_{i}^{0}=(\boldsymbol{x}_{i}^{0},\boldsymbol{v}_{i}^{0})$
as realisations of a random variable
![]() $\boldsymbol{Z}^{0}$
with density
$\boldsymbol{Z}^{0}$
with density
![]() $g_{0}$
.
$g_{0}$
.
Time stepping. The markers evolve along the characteristics of the Vlasov equation so that at time
![]() $t$
the random variable
$t$
the random variable
![]() $\boldsymbol{Z}(t)=(\boldsymbol{X}(t),\boldsymbol{V}(t))$
is distributed according to the density
$\boldsymbol{Z}(t)=(\boldsymbol{X}(t),\boldsymbol{V}(t))$
is distributed according to the density
![]() $g(t,\boldsymbol{z})$
that is the solution of the GK Vlasov equation with initial condition
$g(t,\boldsymbol{z})$
that is the solution of the GK Vlasov equation with initial condition
![]() $g_{0}$
.
$g_{0}$
.
Then, as we saw, the different quantities we need to compute using the Monte Carlo approximation are of the form
for some analytically known function
![]() ${\it\psi}(\boldsymbol{z})$
. This means that we need to simulate the random variable
${\it\psi}(\boldsymbol{z})$
. This means that we need to simulate the random variable
![]() $Y(t)={\it\psi}(\boldsymbol{Z}(t))f(t,\boldsymbol{Z}(t))/g(t,\boldsymbol{Z}(t))={\it\psi}(\boldsymbol{Z}(t))W$
, where the random variable
$Y(t)={\it\psi}(\boldsymbol{Z}(t))f(t,\boldsymbol{Z}(t))/g(t,\boldsymbol{Z}(t))={\it\psi}(\boldsymbol{Z}(t))W$
, where the random variable
![]() $W$
is defined by
$W$
is defined by
![]() $W=f(t,\boldsymbol{Z}(t))/g(t,\boldsymbol{Z}(t))$
. Because
$W=f(t,\boldsymbol{Z}(t))/g(t,\boldsymbol{Z}(t))$
. Because
![]() $f$
and
$f$
and
![]() $g$
are conserved along the same characteristics, we have
$g$
are conserved along the same characteristics, we have
so that the random variable
![]() $W$
does not depend on time and is set once for all at the initialisation.
$W$
does not depend on time and is set once for all at the initialisation.
Using importance sampling, we obtain the so-called weighted PIC method, in which the particles or markers are advanced as in the standard PIC method, but have in addition an importance weight which does not evolve in time. The drawback of this method is that the variance can increase when large importance weights and small importance weights are mixed close together in phase space, which often happens in long nonlinear simulations.
3.5.2. Control variates
We combine here control variates with importance sampling for most generality, but it can also be used without importance sampling by taking
![]() $g_{0}=f_{0}$
.
$g_{0}=f_{0}$
.
In the PIC method, expected values of the form (3.47) cannot be exactly computed because the particle density in phase space
![]() $f(t,\boldsymbol{z})$
is not analytically known except at the initial time. However, in many problems, and in particular in problems we study in magnetic fusion applications, the distribution function stays close to an analytically known distribution function
$f(t,\boldsymbol{z})$
is not analytically known except at the initial time. However, in many problems, and in particular in problems we study in magnetic fusion applications, the distribution function stays close to an analytically known distribution function
![]() $\tilde{f}(t,\boldsymbol{z})$
, which in our applications is typically the initial canonical Maxwellian. Next to the random variable
$\tilde{f}(t,\boldsymbol{z})$
, which in our applications is typically the initial canonical Maxwellian. Next to the random variable
![]() $Y(t)$
associated to
$Y(t)$
associated to
![]() $f(t,\boldsymbol{z})$
, this can be used to build the control variate
$f(t,\boldsymbol{z})$
, this can be used to build the control variate
![]() ${\tilde{Y}}(t)$
associated to
${\tilde{Y}}(t)$
associated to
![]() $\tilde{f}(t,\boldsymbol{z})$
such that
$\tilde{f}(t,\boldsymbol{z})$
such that
Indeed, we have
which can be computed analytically for simple enough functions
![]() ${\it\psi}$
and
${\it\psi}$
and
![]() $\tilde{f}$
. Moreover, if
$\tilde{f}$
. Moreover, if
![]() $\tilde{f}$
is close enough to
$\tilde{f}$
is close enough to
![]() $f$
, then
$f$
, then
![]() ${\tilde{Y}}(t)$
will be close to
${\tilde{Y}}(t)$
will be close to
![]() $Y(t)$
and from the previous discussion a variance reduction of the order of the squared distance between the two random variables can be expected.
$Y(t)$
and from the previous discussion a variance reduction of the order of the squared distance between the two random variables can be expected.
Let us now explain how this can be implemented in a PIC simulation.
Initialisation. As for importance sampling, the initial phase-space positions of the markers are sampled as realisations
![]() $(\boldsymbol{z}_{i}^{0})_{1\leqslant i\leqslant N}$
of the random variable
$(\boldsymbol{z}_{i}^{0})_{1\leqslant i\leqslant N}$
of the random variable
![]() $\boldsymbol{Z}^{0}$
of density
$\boldsymbol{Z}^{0}$
of density
![]() $g_{0}$
. The importance weights are then defined by the corresponding realisations of the random variable
$g_{0}$
. The importance weights are then defined by the corresponding realisations of the random variable
![]() $W=f_{0}(\boldsymbol{Z}^{0})/g_{0}(\boldsymbol{Z}^{0})$
, i.e.
$W=f_{0}(\boldsymbol{Z}^{0})/g_{0}(\boldsymbol{Z}^{0})$
, i.e.
![]() $w_{i}=f_{0}(\boldsymbol{z}_{i}^{0})/g_{0}(\boldsymbol{z}_{i}^{0})$
.
$w_{i}=f_{0}(\boldsymbol{z}_{i}^{0})/g_{0}(\boldsymbol{z}_{i}^{0})$
.
We also initialise the importance weights for
![]() ${\it\delta}f=f-\tilde{f}$
, which are defined by the random variable
${\it\delta}f=f-\tilde{f}$
, which are defined by the random variable
Time stepping. The markers
![]() $\boldsymbol{Z}$
are advanced by numerically solving the characteristics of the GK Vlasov equation. This means that given their positions
$\boldsymbol{Z}$
are advanced by numerically solving the characteristics of the GK Vlasov equation. This means that given their positions
![]() $\boldsymbol{Z}^{n}$
at time
$\boldsymbol{Z}^{n}$
at time
![]() $t_{n}$
, an ordinary differential equation solver is used to compute an approximation of their positions
$t_{n}$
, an ordinary differential equation solver is used to compute an approximation of their positions
![]() $\boldsymbol{Z}^{n+1}$
at time
$\boldsymbol{Z}^{n+1}$
at time
![]() $t^{n+1}$
. Because
$t^{n+1}$
. Because
![]() $f$
and
$f$
and
![]() $g$
satisfy the same GK Vlasov equation, they are conserved along the same characteristics so that, as for importance sampling,
$g$
satisfy the same GK Vlasov equation, they are conserved along the same characteristics so that, as for importance sampling,
is a random variable which does not depend on time. On the other hand, we know
![]() $\tilde{f}$
analytically and know that
$\tilde{f}$
analytically and know that
![]() $f$
and
$f$
and
![]() $g$
are conserved along the characteristics, so that we can compute the importance weight for
$g$
are conserved along the characteristics, so that we can compute the importance weight for
![]() ${\it\delta}f$
at time
${\it\delta}f$
at time
![]() $t_{n}$
from the phase-space positions of the markers at the same time:
$t_{n}$
from the phase-space positions of the markers at the same time:
So,
![]() $W_{{\it\alpha}}^{n}$
is a time-dependent random variable which can be computed explicitly using the analytical functions
$W_{{\it\alpha}}^{n}$
is a time-dependent random variable which can be computed explicitly using the analytical functions
![]() $\tilde{f}$
,
$\tilde{f}$
,
![]() $f_{0}$
and
$f_{0}$
and
![]() $g_{0}$
. These values can be used to express the sample mean for the new simulated random variable
$g_{0}$
. These values can be used to express the sample mean for the new simulated random variable
![]() ${\tilde{Y}}_{{\it\alpha}}=Y-{\it\alpha}({\tilde{Y}}-\mathbb{E}({\tilde{Y}}))$
. This is defined by
${\tilde{Y}}_{{\it\alpha}}=Y-{\it\alpha}({\tilde{Y}}-\mathbb{E}({\tilde{Y}}))$
. This is defined by
Inserting the values for
![]() $Y_{i}^{n}$
and
$Y_{i}^{n}$
and
![]() ${\tilde{Y}}_{i}^{n}$
, we get
${\tilde{Y}}_{i}^{n}$
, we get
This yields an estimator for
![]() ${\it\psi}(\boldsymbol{Z})$
based on the weights
${\it\psi}(\boldsymbol{Z})$
based on the weights
![]() $W_{{\it\alpha}}^{n}$
and the expected value that can be computed analytically,
$W_{{\it\alpha}}^{n}$
and the expected value that can be computed analytically,
![]() $\mathbb{E}({\tilde{Y}})$
. If no estimation of the optimal
$\mathbb{E}({\tilde{Y}})$
. If no estimation of the optimal
![]() ${\it\alpha}^{\ast }$
is available, this method is used with
${\it\alpha}^{\ast }$
is available, this method is used with
![]() ${\it\alpha}=1$
.
${\it\alpha}=1$
.
This is classically known as the
![]() ${\it\delta}f$
method in the PIC literature (Aydemir Reference Aydemir1994; Hu & Krommes Reference Hu and Krommes1994; Kotschenreuther Reference Kotschenreuther1988; Allfrey & Hatzky Reference Allfrey and Hatzky2003), as its interest lies in the expression
${\it\delta}f$
method in the PIC literature (Aydemir Reference Aydemir1994; Hu & Krommes Reference Hu and Krommes1994; Kotschenreuther Reference Kotschenreuther1988; Allfrey & Hatzky Reference Allfrey and Hatzky2003), as its interest lies in the expression
![]() $f=\tilde{f}+{\it\delta}f$
with
$f=\tilde{f}+{\it\delta}f$
with
![]() $\tilde{f}$
known. A large variance reduction for
$\tilde{f}$
known. A large variance reduction for
![]() ${\it\alpha}=1$
is obtained as long as
${\it\alpha}=1$
is obtained as long as
![]() ${\it\delta}f\ll \tilde{f}$
, else one can also achieve some variance reduction by optimising for
${\it\delta}f\ll \tilde{f}$
, else one can also achieve some variance reduction by optimising for
![]() ${\it\alpha}$
(Kleiber et al.
Reference Kleiber, Hatzky, Könies, Kauffmann and Helander2011).
${\it\alpha}$
(Kleiber et al.
Reference Kleiber, Hatzky, Könies, Kauffmann and Helander2011).
3.6. Monte Carlo PIC discretisation of the GK equations
We are now ready to proceed with the Monte Carlo PIC discretisation of the GK equations with the discrete Lagrangian equation (3.27) as a starting point.
Keeping the possibility of using importance sampling, we choose an initial marker distribution
![]() $g_{0}$
based on physics considerations rather than the actual initial particle distribution
$g_{0}$
based on physics considerations rather than the actual initial particle distribution
![]() $f_{0}$
. We then compute samples from a random variable
$f_{0}$
. We then compute samples from a random variable
![]() $\boldsymbol{Z}$
distributed with probability density
$\boldsymbol{Z}$
distributed with probability density
![]() $g_{0}$
. These will be the initial marker phase space positions
$g_{0}$
. These will be the initial marker phase space positions
![]() $\boldsymbol{z}_{k}^{0}$
. After that, we compute the importance weights for each marker
$\boldsymbol{z}_{k}^{0}$
. After that, we compute the importance weights for each marker
![]() $w_{k}=f_{0}(\boldsymbol{z}_{k})/g_{0}(\boldsymbol{z}_{k})$
which do not evolve during the simulation.
$w_{k}=f_{0}(\boldsymbol{z}_{k})/g_{0}(\boldsymbol{z}_{k})$
which do not evolve during the simulation.
In order to get the equations of motion of the markers, we compute the Euler–Lagrange equations associated to the Lagrangian equation (3.27) with respect to the components of the markers phase space positions
![]() $z_{k}^{{\it\alpha}}$
. This yields exactly the same equations as (2.27)–(2.28) that can be inverted as in the continuous case, which yields the equations of motion for the markers:
$z_{k}^{{\it\alpha}}$
. This yields exactly the same equations as (2.27)–(2.28) that can be inverted as in the continuous case, which yields the equations of motion for the markers:
These can be computed by solving the polarisation equation on a grid of physical space, after having constructed the charge density
![]() ${\it\rho}=\int \text{d}W\,e\text{J}_{0}\,f$
on the grid.
${\it\rho}=\int \text{d}W\,e\text{J}_{0}\,f$
on the grid.
We consider the expression of the gyrocentre density:
3.7. Polarisation equation using finite elements
In the continuous case, the variational form of the polarisation equation is given by (2.38). Exactly the same equation, replacing
![]() ${\it\Phi}$
by its finite-element approximation
${\it\Phi}$
by its finite-element approximation
![]() ${\it\Phi}_{h}$
, can be obtained by constraining the variations
${\it\Phi}_{h}$
, can be obtained by constraining the variations
![]() ${\it\delta}{\it\Phi}$
to be in the same finite-element space as
${\it\delta}{\it\Phi}$
to be in the same finite-element space as
![]() ${\it\Phi}_{h}$
. Another way to obtain the discrete equation, which might be more appealing for people not familiar with functional derivatives, consists in taking the Euler–Lagrange equations with respect to the coefficients
${\it\Phi}_{h}$
. Another way to obtain the discrete equation, which might be more appealing for people not familiar with functional derivatives, consists in taking the Euler–Lagrange equations with respect to the coefficients
![]() ${\it\Phi}_{{\it\nu}}$
of
${\it\Phi}_{{\it\nu}}$
of
in the discrete Lagrangian equation (3.27). As
![]() $\dot{{\it\Phi}}_{{\it\mu}}$
does not appear in the Lagrangian, this reduces to
$\dot{{\it\Phi}}_{{\it\mu}}$
does not appear in the Lagrangian, this reduces to
which can be written, taking
![]() $\sum {\it\Phi}_{m}u$
out of the integral,
$\sum {\it\Phi}_{m}u$
out of the integral,
The previous equation is actually a set of linear equations:
with
When adiabatic electrons were used, the discretised polarisation equation has the form
The computation of
![]() $b_{{\it\nu}}$
is called charge assignment: the charge density is obtained by assigning the weights to gyrorings and projecting them on the B-spline basis. Let us now describe more precisely how this is done.
$b_{{\it\nu}}$
is called charge assignment: the charge density is obtained by assigning the weights to gyrorings and projecting them on the B-spline basis. Let us now describe more precisely how this is done.
3.8. Gyroaverage
The calculation of
![]() ${\it\rho}_{N}$
is complicated by the appearance of the gyroaverage operator
${\it\rho}_{N}$
is complicated by the appearance of the gyroaverage operator
![]() $\text{J}_{0}$
. In general, given a scalar field
$\text{J}_{0}$
. In general, given a scalar field
![]() ${\it\Phi}(\boldsymbol{R})$
, the gyroaverage operator
${\it\Phi}(\boldsymbol{R})$
, the gyroaverage operator
![]() $\text{J}_{0}{\it\Phi}$
is defined as
$\text{J}_{0}{\it\Phi}$
is defined as
where
![]() $\hat{{\it\Phi}}$
is the Fourier-transformed potential and
$\hat{{\it\Phi}}$
is the Fourier-transformed potential and
![]() ${\it\rho}_{i}=(k_{B}Tmc^{2})(e^{2}B^{2})$
. The previous equation shows that the operator
${\it\rho}_{i}=(k_{B}Tmc^{2})(e^{2}B^{2})$
. The previous equation shows that the operator
![]() $\text{J}_{0}$
has the form, in Fourier space, of a multiplication of Fourier coefficients by the zeroth Bessel functions
$\text{J}_{0}$
has the form, in Fourier space, of a multiplication of Fourier coefficients by the zeroth Bessel functions
![]() $\text{J}_{0}(k_{\bot }{\it\rho}_{i})$
. This means that direct calculation of
$\text{J}_{0}(k_{\bot }{\it\rho}_{i})$
. This means that direct calculation of
![]() $\text{J}_{0}{\it\Phi}$
for each individual marker has to account for its interaction with all the waves in the system. Therefore, the exact calculation of
$\text{J}_{0}{\it\Phi}$
for each individual marker has to account for its interaction with all the waves in the system. Therefore, the exact calculation of
![]() $\text{J}_{0}$
is computationally prohibitive. Alternatively, the gyroaverage procedure can be approximated by an average over a number of points on the gyroring (Lee Reference Lee1987). When four quadrature points are used, this procedure is rigorously equivalent to considering the Taylor expansion
$\text{J}_{0}$
is computationally prohibitive. Alternatively, the gyroaverage procedure can be approximated by an average over a number of points on the gyroring (Lee Reference Lee1987). When four quadrature points are used, this procedure is rigorously equivalent to considering the Taylor expansion
![]() $\text{J}_{0}(k_{\bot }{\it\rho}_{i})\simeq 1-(k_{\bot }{\it\rho}_{i})^{2}/4$
and computing the transverse Laplacian using second-order finite differences. A simple proof can be given when considering a uniform 2D grid, with grid spacing
$\text{J}_{0}(k_{\bot }{\it\rho}_{i})\simeq 1-(k_{\bot }{\it\rho}_{i})^{2}/4$
and computing the transverse Laplacian using second-order finite differences. A simple proof can be given when considering a uniform 2D grid, with grid spacing
![]() $h={\it\rho}_{i}$
in both directions. Each point of the grid is defined by a pair of indices
$h={\it\rho}_{i}$
in both directions. Each point of the grid is defined by a pair of indices
![]() $(i,j)$
:
$(i,j)$
:
 $$\begin{eqnarray}\displaystyle \text{J}_{0}(\boldsymbol{R}) & \simeq & \displaystyle {\it\Phi}-\frac{1}{4}{\it\rho}_{i}^{2}{\rm\nabla}_{\bot }^{2}{\it\Phi}(\boldsymbol{R})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{J}_{0}{\it\Phi}_{i,j}\simeq {\it\Phi}_{ij}+\frac{{\it\rho}_{i}^{2}}{4h^{2}}({\it\Phi}_{i+1,j}+{\it\Phi}_{i-1,j}+{\it\Phi}_{i,j+1}+{\it\Phi}_{i,j-1}-4{\it\Phi}_{i,j})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4}({\it\Phi}_{i+1,j}+{\it\Phi}_{i-1,j}+{\it\Phi}_{i,j+1}+{\it\Phi}_{i,j-1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{J}_{0}(\boldsymbol{R}) & \simeq & \displaystyle {\it\Phi}-\frac{1}{4}{\it\rho}_{i}^{2}{\rm\nabla}_{\bot }^{2}{\it\Phi}(\boldsymbol{R})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{J}_{0}{\it\Phi}_{i,j}\simeq {\it\Phi}_{ij}+\frac{{\it\rho}_{i}^{2}}{4h^{2}}({\it\Phi}_{i+1,j}+{\it\Phi}_{i-1,j}+{\it\Phi}_{i,j+1}+{\it\Phi}_{i,j-1}-4{\it\Phi}_{i,j})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4}({\it\Phi}_{i+1,j}+{\it\Phi}_{i-1,j}+{\it\Phi}_{i,j+1}+{\it\Phi}_{i,j-1}),\end{eqnarray}$$
where the standard second order centres finite difference scheme
![]() ${\rm\nabla}^{2}{\it\Phi}_{j}=(-{\it\Phi}_{j+1}+2{\it\Phi}_{j}-{\it\Phi}_{j}-1)/h^{2}$
was used. In general, the number of points used in the quadrature is linearly increased with the gyroradius
${\rm\nabla}^{2}{\it\Phi}_{j}=(-{\it\Phi}_{j+1}+2{\it\Phi}_{j}-{\it\Phi}_{j}-1)/h^{2}$
was used. In general, the number of points used in the quadrature is linearly increased with the gyroradius
![]() ${\it\rho}_{i}$
to guarantee the same number of points per arc length on the gyroring:
${\it\rho}_{i}$
to guarantee the same number of points per arc length on the gyroring:
where
![]() $N_{gr}({\it\rho}_{i})$
is the number of points on the gyroring chosen for the average and
$N_{gr}({\it\rho}_{i})$
is the number of points on the gyroring chosen for the average and
![]() $\hat{{\it\Phi}}_{{\it\beta}}$
represents the value of the electrostatic potential on the
$\hat{{\it\Phi}}_{{\it\beta}}$
represents the value of the electrostatic potential on the
![]() ${\it\beta}$
point on the gyroring. In practice, this gyroaverage is applied to a finite-element basis function
${\it\beta}$
point on the gyroring. In practice, this gyroaverage is applied to a finite-element basis function
![]() ${\it\Lambda}_{{\it\nu}}$
to compute the right-hand side
${\it\Lambda}_{{\it\nu}}$
to compute the right-hand side
![]() $b_{{\it\nu}}$
of the discrete polarisation equation as defined in (3.64).
$b_{{\it\nu}}$
of the discrete polarisation equation as defined in (3.64).
3.9. Control variate
In addition to importance sampling, considerable noise reduction can be achieved by applying the control variate technique discussed in § 3.5.2 in order to compute the right-hand side
![]() $b_{{\it\nu}}$
of the discrete polarisation equation defined in (3.64).
$b_{{\it\nu}}$
of the discrete polarisation equation defined in (3.64).
The natural choice for the probability density used to define the control variate is
![]() $\tilde{f}$
, a solution of the unperturbed equations of motion, typically a Maxwellian distribution function. We shall consider only the case
$\tilde{f}$
, a solution of the unperturbed equations of motion, typically a Maxwellian distribution function. We shall consider only the case
![]() ${\it\alpha}=1$
, which is used in practice most of the time. Then the initial importance weights for
${\it\alpha}=1$
, which is used in practice most of the time. Then the initial importance weights for
![]() ${\it\delta}f=f-\tilde{f}$
of the markers that we denote by
${\it\delta}f=f-\tilde{f}$
of the markers that we denote by
![]() $w_{k}^{{\it\alpha}}$
become, using (3.51),
$w_{k}^{{\it\alpha}}$
become, using (3.51),
The right-hand side of the discretised polarisation equation becomes
The quasi-neutrality condition at
![]() $t=0$
implies that the first term on the left-hand side must vanish. When adiabatic electrons are used, we have
$t=0$
implies that the first term on the left-hand side must vanish. When adiabatic electrons are used, we have
Therefore, the fluid electron density
![]() $n_{0e}$
must be carefully chosen to match:
$n_{0e}$
must be carefully chosen to match:
The weights can now vary in time. They can be updated using (3.53)
Another possibility of updating the
![]() ${\it\delta}f$
weights, especially useful for linear simulations, would be to derive an evolution equation for them using the GK Vlasov equation:
${\it\delta}f$
weights, especially useful for linear simulations, would be to derive an evolution equation for them using the GK Vlasov equation:
4. Results
All the simulations presented in this work have been performed using the code NEMORB (Bottino et al. Reference Bottino, Scott, Brunner, McMillan, Tran, Vernay, Villard, Jolliet, Hatzky and Peeters2010), a multi-species electromagnetic extension of ORB5 (Jolliet et al. Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007). The linearised field equations, the polarisation equation and the parallel Ampère’s law are discretised using B-splines. The code is based on straight-field-line coordinates and includes collision operators (Vernay et al. Reference Vernay, Brunner, Villard, McMillan, Jolliet, Tran, Bottino and Graves2010), shaped MHD equilibria and a hybrid model for the trapped electrons (Bottino et al. Reference Bottino, Peeters, Sauter, Vaclavik and Villard2004, Reference Bottino, Sauter, Camenen and Fable2006; Vernay et al. Reference Vernay, Brunner, Villard, McMillan, Jolliet, Bottino, Görler and Jenko2013). The NEMORB gyrokinetic model, in the electrostatic limit, is based on the gyrokinetic Vlasov–Poisson system of equations described in the previous section:
modified to enforce conservation of the number of particles. The symbol ˜ stands for the operator which projects a general function
![]() $A(\boldsymbol{R},p_{\Vert },{\it\mu},t)$
to a reduced space
$A(\boldsymbol{R},p_{\Vert },{\it\mu},t)$
to a reduced space
![]() $\tilde{A}({\it\psi},{\it\epsilon},t)$
, where
$\tilde{A}({\it\psi},{\it\epsilon},t)$
, where
![]() ${\it\psi}$
is the poloidal magnetic flux and
${\it\psi}$
is the poloidal magnetic flux and
![]() ${\it\epsilon}$
is the kinetic energy. The complete definitions of the projection operator and of the heat source
${\it\epsilon}$
is the kinetic energy. The complete definitions of the projection operator and of the heat source
![]() $S_{H}$
are given by Vernay et al. (Reference Vernay, Brunner, Villard, McMillan, Jolliet, Tran and Bottino2012). This source term tends to readjust the temperature profile towards the background profile. Note that small profile variations are still allowed during the simulation.
$S_{H}$
are given by Vernay et al. (Reference Vernay, Brunner, Villard, McMillan, Jolliet, Tran and Bottino2012). This source term tends to readjust the temperature profile towards the background profile. Note that small profile variations are still allowed during the simulation.
4.1. Numerical analysis of the statistical noise
As previously discussed, the Monte Carlo error for the approximation of the expected value of a random variable
![]() $X$
is proportional to
$X$
is proportional to
![]() ${\it\sigma}(X)/\sqrt{N}$
. In PIC simulations, this translates into the so-called ‘statistical noise’ introduced when moments of the distribution function (for example, the charge assignment) are computed using a finite number of markers. The code ORB5 allows for a direct evaluation of the noise contribution to the charge assignment,
${\it\sigma}(X)/\sqrt{N}$
. In PIC simulations, this translates into the so-called ‘statistical noise’ introduced when moments of the distribution function (for example, the charge assignment) are computed using a finite number of markers. The code ORB5 allows for a direct evaluation of the noise contribution to the charge assignment,
![]() ${\it\rho}_{noise}$
(Bottino et al.
Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007). This measure is based on the average amplitude of the contribution to the charge density,
${\it\rho}_{noise}$
(Bottino et al.
Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007). This measure is based on the average amplitude of the contribution to the charge density,
![]() $|{\it\rho}_{k}|$
, of the non-resonant (filtered) modes which are physically damped and whose amplitude arises merely from noise. Figure 3 shows an example of the time evolution of the volume-averaged
$|{\it\rho}_{k}|$
, of the non-resonant (filtered) modes which are physically damped and whose amplitude arises merely from noise. Figure 3 shows an example of the time evolution of the volume-averaged
![]() ${\it\rho}_{noise}$
for a set of simulations with different total numbers of markers. Through the comparison with the charge density of the ‘physical’ modes, a signal to noise ratio can be constructed. This diagnostics provides a direct indicator of the quality of the numerical simulations during all the time evolution. The amplitude of
${\it\rho}_{noise}$
for a set of simulations with different total numbers of markers. Through the comparison with the charge density of the ‘physical’ modes, a signal to noise ratio can be constructed. This diagnostics provides a direct indicator of the quality of the numerical simulations during all the time evolution. The amplitude of
![]() ${\it\rho}_{noise}$
can be analytically estimated in several ways (see, for example Nevins et al.
Reference Nevins, Parker, Chen, Candy, Dimits, Dorland, Hammett and Jenko2005). In the case of ORB5, a simple expression has been given by Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007):
${\it\rho}_{noise}$
can be analytically estimated in several ways (see, for example Nevins et al.
Reference Nevins, Parker, Chen, Candy, Dimits, Dorland, Hammett and Jenko2005). In the case of ORB5, a simple expression has been given by Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007):
where
![]() $N_{p}$
is the number of markers,
$N_{p}$
is the number of markers,
![]() $N_{G}$
is the number of modes kept in the simulation and
$N_{G}$
is the number of modes kept in the simulation and
![]() $w_{i}$
is the weight of a single marker. The full derivation of the previous equation is reported in appendix A. This equation indicates that the statistical noise can be reduced either by increasing the number of markers (
$w_{i}$
is the weight of a single marker. The full derivation of the previous equation is reported in appendix A. This equation indicates that the statistical noise can be reduced either by increasing the number of markers (
![]() $\sqrt{N_{p}}$
convergence) or by reducing the number of Fourier modes kept in the simulations (Fourier filtering of non-resonant modes). Several ORB5 simulations showed that the scaling of the noise in the number of particles per mode,
$\sqrt{N_{p}}$
convergence) or by reducing the number of Fourier modes kept in the simulations (Fourier filtering of non-resonant modes). Several ORB5 simulations showed that the scaling of the noise in the number of particles per mode,
![]() $N_{p}/N_{G}$
, is in excellent agreement with the estimate, as is illustrated in figure 4, where
$N_{p}/N_{G}$
, is in excellent agreement with the estimate, as is illustrated in figure 4, where
![]() ${\it\rho}_{noise}^{2}/\langle w^{2}\rangle$
is plotted as a function of time for the simulations of figure 4. Moreover, the scaling of the noise with the number of particles shows that the important parameter in PIC simulations is indeed the number of particles per Fourier mode and not the number of particles per grid cell (figure 5). The function
${\it\rho}_{noise}^{2}/\langle w^{2}\rangle$
is plotted as a function of time for the simulations of figure 4. Moreover, the scaling of the noise with the number of particles shows that the important parameter in PIC simulations is indeed the number of particles per Fourier mode and not the number of particles per grid cell (figure 5). The function
![]() $G$
accounts for additional filtering coming through finite Larmor radius (FLR) effects and the grid projection algorithm. However, it is important to stress the role of the
$G$
accounts for additional filtering coming through finite Larmor radius (FLR) effects and the grid projection algorithm. However, it is important to stress the role of the
![]() $G$
function: although the number of numerical particles per mode is a universal scaling for the noise in PIC codes, the scaling factor, i.e. the
$G$
function: although the number of numerical particles per mode is a universal scaling for the noise in PIC codes, the scaling factor, i.e. the
![]() $G$
function, is strongly algorithm-dependent, and therefore code-dependent. For example, different projection algorithms in the charge-assignment procedure can lead to very different levels of noise: in ORB5 the level of noise is strongly reduced when moving from linear to cubic finite elements, as illustrated in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
$G$
function, is strongly algorithm-dependent, and therefore code-dependent. For example, different projection algorithms in the charge-assignment procedure can lead to very different levels of noise: in ORB5 the level of noise is strongly reduced when moving from linear to cubic finite elements, as illustrated in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).

Figure 3. Time evolution of the spatial-averaged
![]() ${\it\rho}_{noise}$
for different numbers of markers for a circular cross-section plasma with
${\it\rho}_{noise}$
for different numbers of markers for a circular cross-section plasma with
![]() ${\it\rho}^{\ast }=1/80$
. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
${\it\rho}^{\ast }=1/80$
. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).

Figure 4. Scaling of
![]() ${\it\rho}_{noise}^{2}/\langle w^{2}\rangle$
in
${\it\rho}_{noise}^{2}/\langle w^{2}\rangle$
in
![]() $N_{g}/N_{p}$
for a circular cross-section plasma with
$N_{g}/N_{p}$
for a circular cross-section plasma with
![]() ${\it\rho}^{\ast }=1/80$
. The numbers in the inset caption indicate the number of markers per mode present in the different simulations. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
${\it\rho}^{\ast }=1/80$
. The numbers in the inset caption indicate the number of markers per mode present in the different simulations. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
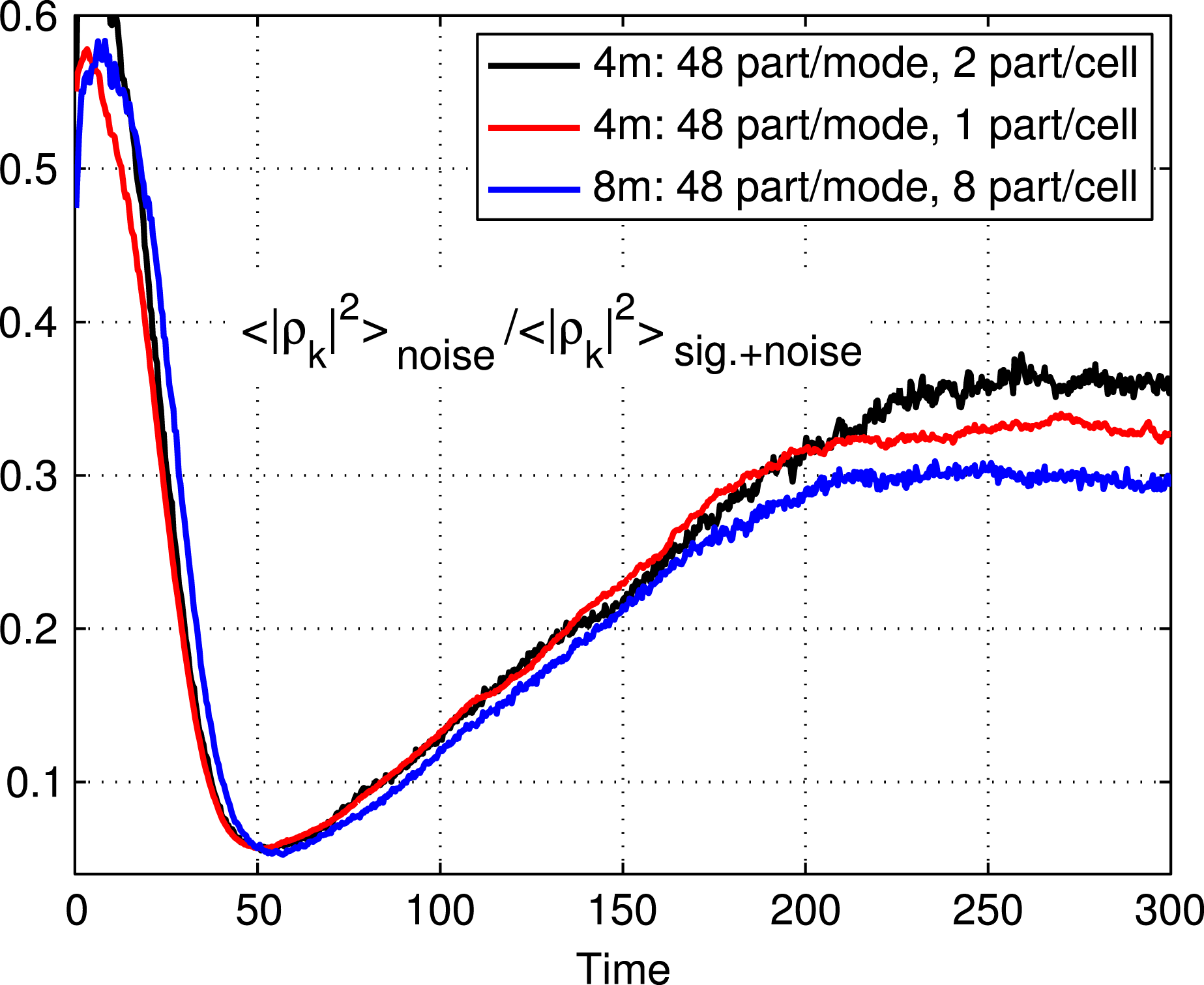
Figure 5. Noise to signal ratio for simulations with same number of markers per mode but different numbers of markers per grid point for a circular cross-section plasma with
![]() ${\it\rho}^{\ast }=1/80$
. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
${\it\rho}^{\ast }=1/80$
. Numerical and physical parameters can be found in Bottino et al. (Reference Bottino, Peeters, Hatzky, Jolliet, McMillan, Tran and Villard2007).
4.2. Convergence in number of particles
The NEMORB simulations presented in this section are based on parameters and profiles of the ITM Cyclone base case (Falchetto et al.
Reference Falchetto, Scott, Angelino, Bottino, Dannert, Grandgirard, Janhunen, Jenko, Jolliet, Kendl, McMillan, Naulin, Nielsen, Ottaviani, Peeters, Pueschel, Reiser, Ribeiro and Romanelli2008). This is a standard benchmark case based on a circular low-
![]() ${\it\beta}$
equilibrium, deuterium plasma,
${\it\beta}$
equilibrium, deuterium plasma,
![]() ${\it\rho}\ast \simeq 1/185$
(mid radius),
${\it\rho}\ast \simeq 1/185$
(mid radius),
![]() $T_{e}=T_{D}$
and flat initial
$T_{e}=T_{D}$
and flat initial
![]() $R/L_{T}$
profiles of
$R/L_{T}$
profiles of
![]() $0.2<s<0.8$
,
$0.2<s<0.8$
,
![]() $s\propto \sqrt{{\it\psi}}$
;
$s\propto \sqrt{{\it\psi}}$
;
![]() ${\it\rho}\ast \equiv {\it\rho}_{s}/a$
is the ion sound Larmor radius normalised to the tokamak minor radius. The
${\it\rho}\ast \equiv {\it\rho}_{s}/a$
is the ion sound Larmor radius normalised to the tokamak minor radius. The
![]() $q$
profile is parabolic, matching the local value of the local Cyclone case (
$q$
profile is parabolic, matching the local value of the local Cyclone case (
![]() $q=1.4$
) at mid radius. A detailed description of the physical parameters and profiles can be found in Falchetto et al. (Reference Falchetto, Scott, Angelino, Bottino, Dannert, Grandgirard, Janhunen, Jenko, Jolliet, Kendl, McMillan, Naulin, Nielsen, Ottaviani, Peeters, Pueschel, Reiser, Ribeiro and Romanelli2008) and Wersal et al. (Reference Wersal, Bottino, Angelino and Scott2012). Figure 6 shows the results of a scan on the initial temperature gradient, with all the other parameters kept fixed. Those simulations are equivalent, in terms of physics and numerical parameters, to the standard ITM global case of Falchetto et al. (Reference Falchetto, Scott, Angelino, Bottino, Dannert, Grandgirard, Janhunen, Jenko, Jolliet, Kendl, McMillan, Naulin, Nielsen, Ottaviani, Peeters, Pueschel, Reiser, Ribeiro and Romanelli2008), except for the presence of the heat source preventing profile relaxation. The ion heat diffusivity in gyro-Bohm units (
$q=1.4$
) at mid radius. A detailed description of the physical parameters and profiles can be found in Falchetto et al. (Reference Falchetto, Scott, Angelino, Bottino, Dannert, Grandgirard, Janhunen, Jenko, Jolliet, Kendl, McMillan, Naulin, Nielsen, Ottaviani, Peeters, Pueschel, Reiser, Ribeiro and Romanelli2008) and Wersal et al. (Reference Wersal, Bottino, Angelino and Scott2012). Figure 6 shows the results of a scan on the initial temperature gradient, with all the other parameters kept fixed. Those simulations are equivalent, in terms of physics and numerical parameters, to the standard ITM global case of Falchetto et al. (Reference Falchetto, Scott, Angelino, Bottino, Dannert, Grandgirard, Janhunen, Jenko, Jolliet, Kendl, McMillan, Naulin, Nielsen, Ottaviani, Peeters, Pueschel, Reiser, Ribeiro and Romanelli2008), except for the presence of the heat source preventing profile relaxation. The ion heat diffusivity in gyro-Bohm units (
![]() ${\it\chi}_{GB}\equiv {\it\rho}_{s}^{2}c_{s}/a$
, with
${\it\chi}_{GB}\equiv {\it\rho}_{s}^{2}c_{s}/a$
, with
![]() $c_{s}^{2}\equiv T_{e}/m_{D}$
and
$c_{s}^{2}\equiv T_{e}/m_{D}$
and
![]() ${\it\rho}_{s}^{2}\equiv T_{e}m_{D}/(eB_{0})^{2}$
) is plotted versus
${\it\rho}_{s}^{2}\equiv T_{e}m_{D}/(eB_{0})^{2}$
) is plotted versus
![]() $R/L_{T}$
; both the quantities correspond to radial averages of
$R/L_{T}$
; both the quantities correspond to radial averages of
![]() $0.4<r/a<0.6$
. Here it is evident that the heat source prevents profile relaxation but still allows for local modifications of the gradient profile. The solid line represents the original Dimits fit for this curve, derived as a fit to the results of the LLNL gyrokinetic flux-tube PIC electrostatic turbulence code Dimits et al. (Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000). The NEMORB results follow the Dimits curve, although with lower diffusion coefficients, as expected by global simulations. They also correctly reproduce the linear
$0.4<r/a<0.6$
. Here it is evident that the heat source prevents profile relaxation but still allows for local modifications of the gradient profile. The solid line represents the original Dimits fit for this curve, derived as a fit to the results of the LLNL gyrokinetic flux-tube PIC electrostatic turbulence code Dimits et al. (Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000). The NEMORB results follow the Dimits curve, although with lower diffusion coefficients, as expected by global simulations. They also correctly reproduce the linear
![]() $R/L_{T}|_{lin}\simeq 4$
and nonlinear critical thresholds
$R/L_{T}|_{lin}\simeq 4$
and nonlinear critical thresholds
![]() $R/L_{T}|_{nonlin}\simeq 6$
. This is particularly evident when considering the simulation with initial
$R/L_{T}|_{nonlin}\simeq 6$
. This is particularly evident when considering the simulation with initial
![]() $R/L_{T}\simeq 5$
(dark green in figure 6): after the initial linear phase, the heat flux drops rapidly to zero, showing that the mode was linearly unstable, but nonlinearly fully stabilised by zonal flow dynamics. The density, temperature, vorticity and potential spectra for a simulation with initial
$R/L_{T}\simeq 5$
(dark green in figure 6): after the initial linear phase, the heat flux drops rapidly to zero, showing that the mode was linearly unstable, but nonlinearly fully stabilised by zonal flow dynamics. The density, temperature, vorticity and potential spectra for a simulation with initial
![]() $R/L_{T}\simeq 10.3$
are presented in figure 7. Time-averaged spectra show evidence of the nonlinear cascades to lower
$R/L_{T}\simeq 10.3$
are presented in figure 7. Time-averaged spectra show evidence of the nonlinear cascades to lower
![]() $k_{{\it\theta}}{\it\rho}_{s}$
. The generalised vorticity, expressed as a frequency, is
$k_{{\it\theta}}{\it\rho}_{s}$
. The generalised vorticity, expressed as a frequency, is
![]() ${\it\Omega}\simeq eB/m_{D}(n_{e}-n_{i})/n_{0}$
; further details can be found in Scott et al. (Reference Scott, Kendl and Ribeiro2010) and in Wersal et al. (Reference Wersal, Bottino, Angelino and Scott2012).
${\it\Omega}\simeq eB/m_{D}(n_{e}-n_{i})/n_{0}$
; further details can be found in Scott et al. (Reference Scott, Kendl and Ribeiro2010) and in Wersal et al. (Reference Wersal, Bottino, Angelino and Scott2012).

Figure 6. Radial-averaged ion heat diffusivity in gyro-Bohm units versus
![]() $R/L_{T}$
for the Cyclone base case with sources. During the saturation phase,
$R/L_{T}$
for the Cyclone base case with sources. During the saturation phase,
![]() ${\it\chi}/{\it\chi}_{GB}$
lies close to the Dimits fit curve. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.
${\it\chi}/{\it\chi}_{GB}$
lies close to the Dimits fit curve. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.

Figure 7. Different time-averaged spectra for the initial
![]() $R/L_{T}\simeq 10.3$
simulations for the Cyclone base case with sources, calculated from 3D data. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.
$R/L_{T}\simeq 10.3$
simulations for the Cyclone base case with sources, calculated from 3D data. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.

Figure 8. Time evolution of the radial-averaged (
![]() $0.5<r/a<0.7$
) signals (left) and time-averaged spectra (right) for density, temperature, vorticity and non-zonal electrostatic potential for the initial
$0.5<r/a<0.7$
) signals (left) and time-averaged spectra (right) for density, temperature, vorticity and non-zonal electrostatic potential for the initial
![]() $R/L_{T}\simeq 10.3$
simulations. Non-converged time traces correspond to flatter spectra. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.
$R/L_{T}\simeq 10.3$
simulations. Non-converged time traces correspond to flatter spectra. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.

Figure 9. Radial- and time-averaged quantities of figure 8, normalised to the 640M marker results, as a function of the number of markers per active mode. Published under license in J. Phys.: Conf. Ser. by IOP publishing Ltd.
The simulation with initial
![]() $R/L_{T}\simeq 10.3$
has been chosen for a systematic study of the convergence in number of markers for real space time traces and for the corresponding spectra. The quantities considered are: density fluctuations, electrostatic potential, temperature fluctuations and vorticity. Spectra have been obtained by performing a time average during the saturation phase of the simulation, while real space data correspond to radial averages of
$R/L_{T}\simeq 10.3$
has been chosen for a systematic study of the convergence in number of markers for real space time traces and for the corresponding spectra. The quantities considered are: density fluctuations, electrostatic potential, temperature fluctuations and vorticity. Spectra have been obtained by performing a time average during the saturation phase of the simulation, while real space data correspond to radial averages of
![]() $0.5<r/a<0.7$
. The convergence results are illustrated in figure 8. For all the quantities considered, non-converged time traces correspond to flat spectra at high
$0.5<r/a<0.7$
. The convergence results are illustrated in figure 8. For all the quantities considered, non-converged time traces correspond to flat spectra at high
![]() $k_{{\it\theta}}{\it\rho}_{s}$
. On the other hand, converged spectra always exhibit a clear power law down to the highest
$k_{{\it\theta}}{\it\rho}_{s}$
. On the other hand, converged spectra always exhibit a clear power law down to the highest
![]() $k_{{\it\theta}}{\it\rho}_{s}$
values kept in the simulation. The most remarkable result is that not all the physically relevant quantities converge with the same rate. Figure 9 summarises the results of figure 8 by normalising the time-averaged quantities to the results of the simulations with the highest number of markers, plotted versus the number of markers per mode kept in the simulation. The electrostatic potential converges much faster than all the other quantities. The slowest converging field is the density fluctuation,
$k_{{\it\theta}}{\it\rho}_{s}$
values kept in the simulation. The most remarkable result is that not all the physically relevant quantities converge with the same rate. Figure 9 summarises the results of figure 8 by normalising the time-averaged quantities to the results of the simulations with the highest number of markers, plotted versus the number of markers per mode kept in the simulation. The electrostatic potential converges much faster than all the other quantities. The slowest converging field is the density fluctuation,
![]() ${\it\delta}n$
. Remarkably, the ion heat flux diffusivity (and the heat fluxes) converge as fast as the potential. Although the heat flux, important for predicting turbulence-induced transport in experiments, requires relatively few markers to converge (20M), comparisons with experimental measurements (for example, with reflectometry data) rely on an accurate description of the density fluctuation spectra. According to our results, the latter requires at least a factor of 10 more markers then what convergence studies based on potentials or fluxes suggest.
${\it\delta}n$
. Remarkably, the ion heat flux diffusivity (and the heat fluxes) converge as fast as the potential. Although the heat flux, important for predicting turbulence-induced transport in experiments, requires relatively few markers to converge (20M), comparisons with experimental measurements (for example, with reflectometry data) rely on an accurate description of the density fluctuation spectra. According to our results, the latter requires at least a factor of 10 more markers then what convergence studies based on potentials or fluxes suggest.
Acknowledgements
The authors would like to thank R. Hatzky, B. Scott, R. Kleiber and A. Könies for useful discussions and C. Wersal for performing some of the NEMORB simulations. The simulations were performed on the IFERC-CSC HELIOS supercomputer, under the ORBFAST project. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement number 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Appendix A. Derivation of a simple analytical estimate for the noise
The amplitude of the statistical noise contribution to the charge density can be analytically derived. Before discussing the derivation in the case of the ORB5 code, a simpler system is considered by neglecting FLR effects, equilibrium profile variation and zonal flow effects and assuming purely adiabatic electrons. In this case, the quasi-neutrality equation becomes
where the ORB5 normalisation for the weights (see Jolliet et al.
Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007) is assumed:
![]() $n_{0}$
is the averaged particle density,
$n_{0}$
is the averaged particle density,
![]() $V$
is the volume and
$V$
is the volume and
![]() $N_{p}$
is the total number of markers. The continuous Fourier transform of the potential is
$N_{p}$
is the total number of markers. The continuous Fourier transform of the potential is
Applying the Fourier transform to the Poisson equation directly yields
The absolute value squared then is
The second term on the right-hand side represents correlations between marker positions and weights and describes the contribution of waves and turbulence to the density. Following Nevins et al. (Reference Nevins, Parker, Chen, Candy, Dimits, Dorland, Hammett and Jenko2005), we assume that the relevant physics is contained in that term while the noise is contained in the first term, which describes the random positioning of the markers. Therefore, the noise can be represented by
In order to compare with the simulation results, it is convenient to use discrete Fourier transforms (DFTs). The relation between the continuous and discrete FTs can easily be derived:
where
![]() ${\it\Delta}_{x}\equiv L_{x}/N_{x}$
,
${\it\Delta}_{x}\equiv L_{x}/N_{x}$
,
![]() ${\it\Delta}_{y}\equiv L_{y}/N_{y}$
and
${\it\Delta}_{y}\equiv L_{y}/N_{y}$
and
![]() ${\it\Delta}_{z}\equiv L_{z}/N_{z}$
describe the grid spacing;
${\it\Delta}_{z}\equiv L_{z}/N_{z}$
describe the grid spacing;
![]() $L_{x}$
,
$L_{x}$
,
![]() $L_{y}$
and
$L_{y}$
and
![]() $L_{z}$
are the sizes of the computational domain in the three spatial directions and
$L_{z}$
are the sizes of the computational domain in the three spatial directions and
![]() $N_{T}\equiv N_{x}N_{y}N_{z}$
is the total number of grid points in configuration space.
$N_{T}\equiv N_{x}N_{y}N_{z}$
is the total number of grid points in configuration space.
The sum
![]() $\sum _{i=1}^{N_{T}}$
symbol represents a sum over the different modes in
$\sum _{i=1}^{N_{T}}$
symbol represents a sum over the different modes in
![]() $x$
-,
$x$
-,
![]() $y$
- and
$y$
- and
![]() $z$
directions. The discrete Fourier transform is defined as
$z$
directions. The discrete Fourier transform is defined as
with
![]() $q_{i}$
an integer number satisfying
$q_{i}$
an integer number satisfying
Using
and similar relations for the other directions, as well as
one arrives at
In ORB5, the charge density is filtered in Fourier space in order to keep only
![]() $N_{G}<N_{T}$
modes, thus removing physically irrelevant modes. Typically, at every radial location only a few poloidal modes are needed, due to the fact that the turbulence aligns with the magnetic field. If we identify the poloidal direction with
$N_{G}<N_{T}$
modes, thus removing physically irrelevant modes. Typically, at every radial location only a few poloidal modes are needed, due to the fact that the turbulence aligns with the magnetic field. If we identify the poloidal direction with
![]() $y$
, only
$y$
, only
![]() $N_{G}\equiv N_{x}N_{y}^{\prime }N_{z}$
, with
$N_{G}\equiv N_{x}N_{y}^{\prime }N_{z}$
, with
![]() $N_{y}^{\prime }<N_{y}$
, modes are kept in the charge density. More details about the Fourier filtering procedure can be found in Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007). Assuming that the statistical noise has a white-noise character and it contributes to all the Fourier modes, the Fourier filtering procedure reduces the numerical noise contribution to the charge density:
$N_{y}^{\prime }<N_{y}$
, modes are kept in the charge density. More details about the Fourier filtering procedure can be found in Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007). Assuming that the statistical noise has a white-noise character and it contributes to all the Fourier modes, the Fourier filtering procedure reduces the numerical noise contribution to the charge density:
Using the previous relations, one can rewrite the noise formula as
We can also use the energy relation of the FFT
to derive the relation for the fluctuations of
![]() ${\it\phi}$
in real space
${\it\phi}$
in real space
where
is the averaged square weight.
This simple noise estimate can be extended to include FLR effects. In this case, the starting point is the right-hand-side of the gyrokinetic polarisation equation of ORB5:
 $$\begin{eqnarray}\displaystyle b_{{\it\nu}} & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}(e\text{J}_{0}{\it\Lambda}_{{\it\nu}}(\boldsymbol{R}_{k}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}\int \text{d}\boldsymbol{x}{\it\Lambda}_{{\it\nu}}(\boldsymbol{x})\int \text{d}\boldsymbol{p}\exp (2{\rm\pi}\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{x})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (-2{\rm\pi}\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{R}_{k})\text{J}_{0}(\boldsymbol{p}\boldsymbol{\cdot }{\bf\rho}_{ik}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{{\it\nu}} & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}(e\text{J}_{0}{\it\Lambda}_{{\it\nu}}(\boldsymbol{R}_{k}))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}\int \text{d}\boldsymbol{x}{\it\Lambda}_{{\it\nu}}(\boldsymbol{x})\int \text{d}\boldsymbol{p}\exp (2{\rm\pi}\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{x})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (-2{\rm\pi}\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{R}_{k})\text{J}_{0}(\boldsymbol{p}\boldsymbol{\cdot }{\bf\rho}_{ik}).\end{eqnarray}$$
Multiplying the previous expression of
![]() $b_{{\it\nu}}$
by the complex conjugate and neglecting the correlation (physical) term, the noise contribution to the right-hand side of the polarisation equation becomes
$b_{{\it\nu}}$
by the complex conjugate and neglecting the correlation (physical) term, the noise contribution to the right-hand side of the polarisation equation becomes
 $$\begin{eqnarray}\displaystyle |b_{{\it\nu}}|^{2} & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}^{2}\int \text{d}\boldsymbol{p}\,\text{d}\boldsymbol{p}^{\prime }\exp (-2{\rm\pi}\text{i}(\boldsymbol{p}-\boldsymbol{p}^{\prime })\boldsymbol{\cdot }\boldsymbol{R}_{k})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(-\frac{k_{\bot }^{2}(\boldsymbol{p}){\it\rho}_{ik}^{2}+k_{\bot }^{\prime 2}(\boldsymbol{p}^{\prime }){\it\rho}_{ik}^{2}}{2}\right)\tilde{{\it\Lambda}}_{{\it\nu}}(-\boldsymbol{p})\tilde{{\it\Lambda}}_{{\it\nu}}^{\dagger }(-\boldsymbol{p}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |b_{{\it\nu}}|^{2} & = & \displaystyle \mathop{\sum }_{sp}\frac{n_{0}V}{N_{p}}\mathop{\sum }_{k=1}^{N_{p}}w_{k}^{2}\int \text{d}\boldsymbol{p}\,\text{d}\boldsymbol{p}^{\prime }\exp (-2{\rm\pi}\text{i}(\boldsymbol{p}-\boldsymbol{p}^{\prime })\boldsymbol{\cdot }\boldsymbol{R}_{k})\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left(-\frac{k_{\bot }^{2}(\boldsymbol{p}){\it\rho}_{ik}^{2}+k_{\bot }^{\prime 2}(\boldsymbol{p}^{\prime }){\it\rho}_{ik}^{2}}{2}\right)\tilde{{\it\Lambda}}_{{\it\nu}}(-\boldsymbol{p})\tilde{{\it\Lambda}}_{{\it\nu}}^{\dagger }(-\boldsymbol{p}^{\prime }),\end{eqnarray}$$
where the following relation has been used:
with
![]() $f_{0}$
a Maxwellian distribution and
$f_{0}$
a Maxwellian distribution and
Due to the randomisation of the marker positions, the previous expression can be further approximated assuming that
giving