Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T13:03:13.049Z Has data issue: false hasContentIssue false
  • English
  • Français

Mode conversion of laser radiation in the presense of a magnetic wiggler

Published online by Cambridge University Press:  13 March 2009

Jetendra Parashar ,
H. D. Pandey  and
R. K. Singh
Jetendra Parashar
Affiliation:
Center for Energy Studies, Indian Institute of Technology, New Delhi 110 016, India
H. D. Pandey
Affiliation:
Center for Energy Studies, Indian Institute of Technology, New Delhi 110 016, India
R. K. Singh
Affiliation:
Department of Physics, Barkatullah University, Bhopal 462 026, M.P., India
Get access Rights & Permissions [Opens in a new window]

Abstract

Laser radiation 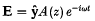propagating through a non-uniform plasma along the direction of the density gradient suffers total reflection at the critical layer. However, when a wiggler magnetic field 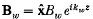exists near the critical layer, the laser drives a Langmuir wave. For suitable values of Bw and kw, the power transfer from the laser to the Langmuir wave could be as high as 60%. The Langmuir wave deposits its energy on the electrons via Landau damping. This may be an efficient mechanism of laser absorption when large self-generated magnetic fields exist in the plasma.

Type
Research Article
Information
Journal of Plasma Physics , Volume 53 , Issue 3 , June 1995 , pp. 285 - 292
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
Ginzburg, V. L. 1960 Propagation of Electromagnetic Waves in Plasmas. Pergamon.Google Scholar
Geebogi, C., Liu, C. S. & Tripathi, V. K. 1977 Phys. Rev. Lett. 39, 338.CrossRefGoogle Scholar
Kruer, W. 1987 The Physics of Laser Plasma Interaction. Addison-Wesley.Google Scholar
Littlejohn, R. G. & Flynn, W. O. 1993 Phys. Rev. Lett. 70, 1799.Google Scholar
Mora, P. & Pellat, R. 1979 Phys. Fluids 22, 2408.Google Scholar
Rowland, H. L. 1992 Phys. Fluids B 4, 3883.CrossRefGoogle Scholar
Stamper, J. A. 1975 Phys. Fluids 18, 735.CrossRefGoogle Scholar
Stamper, J. A., Papadopoulos, K., Sudan, R. N., Mclean, E. A. & Dawson, J. M. 1972 Phys. Rev. Lett. 26, 1012.Google Scholar
Stix, T. H. 1962 The Theory of Plasma Waves. McGraw-Hill.Google Scholar
Sudan, R. N. 1993 Phys. Rev. Lett. 70, 3075.CrossRefGoogle Scholar
Tripathi, V. K. & Liu, C. S. 1982 Phys. Fluids 25, 629.Google Scholar
Tripathi, V. K. & Liu, C. S. 1994 Phys. Plasmas 1, 990.CrossRefGoogle Scholar
Woo, W. & Degroot, J. S. 1978 Phys. Fluids 21, 124.Google Scholar