Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T18:48:18.173Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetic stabilization of transverse plasma instabilitiest†

Published online by Cambridge University Press:  13 March 2009

B. Buti  and
G. S. Lakhina
B. Buti
Affiliation:
Department of Physics, Indian Institute of Technology, New Dethi
G. S. Lakhina
Affiliation:
Department of Physics, Indian Institute of Technology, New Dethi
Get access Rights & Permissions [Opens in a new window]

Abstract

Waves, propagating transverse to the direction of the streaming of a plasma in the presence of a uniform external magnetic field, are unstable if the streaming exceeds a certain minimum value. The magnetic field reduces the growth rate of this instability, and also increases the value of the minimum streaming velocity, above which the system is unstable. The thermal motions in the plasma, however, tend to stabilize the system if the magnetic field is weak (i.e. 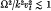, Ω being the electron cyclotron frequency, k the characteristic wave-number, and Vt the thermal velocity); but, in case of strong magnetic field (i.e. 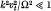), they increase the growth rate, provided 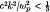(ωp being the electron plasma frequency).

Type
Research Article
Information
Journal of Plasma Physics , Volume 5 , Issue 3 , June 1971 , pp. 467 - 474
Copyright
Copyright © Cambridge University Press 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernstein, I. B. 1958 Phys. Rev. 109, 10.CrossRefGoogle Scholar
Bohm, D. & Gross, E. P. 1949 Phys. Rev. 75, 1851, 1864.CrossRefGoogle Scholar
Bornatici, M. & Lee, K-F. 1970 Phys. Rev. 13, 3007.Google Scholar
Büneman, D. 1963 Ann. Phys. 25, 340.Google Scholar
Büneman, O. 1959 Phys. Rev. 115, 503.Google Scholar
Buti, B. 1963 Phys. Fluids 6, 89.CrossRefGoogle Scholar
Buti, B. & Lakhina, G. S. 1971 Phys-Lett. A. (To be published, March or April.)Google Scholar
Fried, B. D. & Conte, S. D. 1961 The Plasma Dispersion Function. Academic.Google Scholar
Jackson, J. D. 1960 J. Nuc. Energy, C 1, 171.CrossRefGoogle Scholar
Kellog, P. J. & Liemohn, H. 1960 Phys. Fluids 3, 40.Google Scholar
Lee, K-F. 1969 Phys. Rev. 181, 447.CrossRefGoogle Scholar
Momota, H. 1966 Prog. Theoret. Phys. 35, 380.Google Scholar
Watson, G. N. 1948 Theory of Bessel Functions. Cambridge University Press.Google Scholar