Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T09:19:00.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetic field quantization in pulsars

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  23 April 2020

Ch. Rozina Open the ORCID record for Ch. Rozina [Opens in a new window] ,
N. L. Tsintsadze  and
L. N. Tsintsadze
Ch. Rozina*
Affiliation:
Department of Physics, Lahore College for Women University, Lahore 54000, Pakistan
N. L. Tsintsadze
Affiliation:
Faculty of Exact and Natural Sciences, Andronicashvili Institute of Physics, Tbilisi State University, Tbilisi 0105, Georgia
L. N. Tsintsadze
Affiliation:
Faculty of Exact and Natural Sciences, Andronicashvili Institute of Physics, Tbilisi State University, Tbilisi 0105, Georgia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnetic field quantization is an important issue for degenerate environments such as neutron stars, radio pulsars and magnetars etc., due to the fact that these stars have a magnetic field higher than the quantum critical field strength of the order of 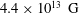$4.4\times 10^{13}~\text{G}$, accordingly, the cyclotron energy may be equal to or even much more than the Fermi energy of degenerate particles. We shall formulate here the exotic physics of strongly magnetized neutron stars, known as pulsars, specifically focusing on the outcomes of the quantized magnetic pressure. In this scenario, while following the modified quantum hydrodynamic model, we shall investigate both linear and nonlinear fast magnetosonic waves in a strongly magnetized, weakly ionized degenerate plasma consisting of neutrons and an electron–ion plasma in the atmosphere of a pulsar. Here, linear analysis depicts that sufficiently long, fast magnetosonic waves may exist in a weakly dispersive pulsar having finite phase speed at cutoff. To investigate one-dimensional nonlinear fast magnetosonic waves, a neutron density expression as a function of both the electron magnetic and neutron degenerate pressures, is derived with the aid of Riemann’s wave solution. Consequently, a modified Korteweg–de Vries equation is derived, having a rarefractive solitary wave solution. It is found that the basic properties such as amplitude, width and phase speed of the fast magnetoacoustic waves are significantly altered by the electron magnetic and the neutron degenerate pressures. The results of this theoretical investigation may be useful for understanding the formation and features of the solitary structures in astrophysical compact objects such as pulsars, magnetars and white dwarfs etc.

Keywords

astrophysical plasmasplasma nonlinear phenomenaquantum plasma
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 2 , April 2020 , 905860211
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdikian, A. & Mahmood, S. 2016 Acoustic solitons in a magnetized quantum electron-positron-ion plasma with relativistic degenerate electrons and positrons pressure. Phys. Plasmas 23, 122303–122309.CrossRefGoogle Scholar
Abrahams, A. M. & Shapiro, S. L. 1991 Equation of state in a strong magnetic field-finite temperature and gradient corrections. Astrophys. J. 374, 652–667.CrossRefGoogle Scholar
Baade, W. & Zwicky, F. 1934 Remarks on super-novae and cosmic rays. Phys. Rev. 46, 76–77.CrossRefGoogle Scholar
Bailes, M. 1989 The origin of pulsar velocities and the velocity magnetic moment correlation. Astrophys. J. 342, 627–629.CrossRefGoogle Scholar
Chabrier, G., Douchin, F. & Potekhin, A. Y. 2002 Dense astrophysical plasmas. J. Phys.: Condens. Matter 14, 9133–9139.Google Scholar
Chabrier, G., Saumon, D. & Potekhin, A. Y. 2006 Dense plasmas in astrophysics: from giant planets to neutron stars. J. Phys. A 39, 4411–4419.Google Scholar
Chamel, N. & Haensel, P. 2008 Physics of neutron star crusts. Living Rev. Relat. 11, 10.CrossRefGoogle ScholarPubMed
Chen, F. 1984 Introduction to Plasma Physics and Controlled Fusion. Plenum Press.CrossRefGoogle Scholar
Haas, F. & Mahmood, S. 2018 Magnetosonic waves in a quantum plasma with arbitrary electron degeneracy. Phys. Rev. E 97, 063206–0632068.Google Scholar
Harding, A. K. & Lai, D. 2006 Physics of strongly magnetized neutron stars. Rep. Prog. Phys. 69, 2631–2708.CrossRefGoogle Scholar
Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F. & Collins, R. A. 1968 Observation of a rapidly pulsating radio source. Nature 217, 709–713.CrossRefGoogle Scholar
Iqbal, Z., Younas, M., Khan, I. A. & Murtaza, G. 2019 Spin magnetoacoustic wave. Phys. Plasmas 26, 112101–112106.CrossRefGoogle Scholar
Kouveliotou, C., Ventura, J. E. & Van Den Heuvel, E. P. 2001 The Neutron Star–Black Hole Connection. Springer.CrossRefGoogle Scholar
Lai, D. 2001 Matter in strong magnetic fields. Rev. Mod. Phys. 73, 629–662.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon Press.Google Scholar
Lewin, W. H. G. & Van Der Klis, M. 2005 Compact Stellar x-ray Sources. Cambridge University Press.Google Scholar
Lui, H.-F., Wang, S.-Q., Wang, Z.-H., Li, C. Z., Yao, L. & Yang, F.-Z. 2011 Two dimensional cylindrical fast magnetoacoustic solitary waves in a dust plasma. Phys. Plasmas 18, 044501–044503.Google Scholar
Lui, H.-F., Wang, S.-Q. & Yang, F.-Z. 2013 Propagation of two dimensional cylindrical fast magnetoacoustic solitary waves in a warm dust plasma. Astrophys. Space Sci. 347, 139–143.Google Scholar
Marklund, M., Eliasson, B. & Shukla, P. K. 2007 Magnetosonic solitons in a fermionic quantum plasma. Phys. Rev. E 76, 067401–067404.Google Scholar
Masood, W., Jhangir, R., Eliasson, B. & Siddiq, M. 2014 A nonlinear model for magnetoacoustic waves in dense dissipative plasmas with degenerate electrons. Phys. Plasmas 21, 102311–102314.CrossRefGoogle Scholar
Masood, W., Jehan, N. & Mirza, A. M. 2010 A new equation in two dimensional fast magnetoacoustic shock waves in electron-positron-ion plasmas. Phys. Plasmas 17, 032314–032316.CrossRefGoogle Scholar
Masood, W., Shah, H., Mushtaq, A. & Salimullah, M. 2009 Linear and nonlinear properties of an obliquely propagating dust magnetosonic wave. J. Plasma Phys. 75, 217–233.CrossRefGoogle Scholar
Massey, H. S. W. 1976 Negative Ions. Cambridge University Press.Google Scholar
Sagdeev, R. 1966 Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23.Google Scholar
Shah, H. A., Iqbal, M. J., Tsintsadze, N. L., Masood, W. & Qureshi, M. N. S. 2012 Effect of trapping in a degenerate plasma in the presence of a quantizing magnetic field. Phys. Plasmas 19, 092304–092308.CrossRefGoogle Scholar
Shukla, P. K., Mamun, A. A. & Mendis, D. A. 2011 Nonlinear ion modes in a dense plasma with strongly coupled ions and degenerate electron fluids. Phys. Rev. E 84, 026405–026406.CrossRefGoogle Scholar
Stenflo, L., Tsintsadze, N. L. & Buadze, T. D. 1989 Solitary acoustic waves in weakly ionized gases. Phys. Lett. A 135, 37–38.CrossRefGoogle Scholar
Tsintsadze, L. N. 2010 Quantization and excitation of longitudinal electrostatic waves in magnetized quantum plasmas. In AIP Conference Proceedings, vol. 1306, pp. 89–102. AIP.Google Scholar
Tsintsadze, L. N., Hussain, A. & Murtaza, G. 2011 New longitudinal waves in electron-positron-ion quantum plasmas. Eur. Phys. J. D 64, 447–452.Google Scholar
Tsintsadze, N. L., Rozina, Ch., Ruby, R. & Tsintsadze, L. N. 2018 Jeans anisotropic instability. Phys. Plasma 25, 073705–073706.CrossRefGoogle Scholar
Tsintsadze, N. L., Rozina, Ch., Shah, H. A. & Murtaza, G. 2008 Jeans instability in a magneto-radiative dusty plasma. J. Plasma Phys. 74, 847–853.CrossRefGoogle Scholar
Tsintsadze, N. L. & Tsintsadze, L. N. 2009a Novel quantum kinetic equations of the Fermi particles. Europhys. Lett. 88, 35001–35004.CrossRefGoogle Scholar
Tsintsadze, N. L. & Tsintsadze, L. N. 2009b From Leonardo to ITER: nonlinear and coherence aspects. In AIP Proceedings NCP, vol. 1177. AIP.Google Scholar
Tsintsadze, L. N. & Tsintsadze, N. L. 2010 Excitation of longitudinal waves in a degenerate isotropic quantum plasma. In AIP Conference Proceedings, vol. 76, pp. 403–408. AIP.Google Scholar
Tsintsadze, N. L. & Tsintsadze, L. N.2012 arXiv:1212.2830 [physics.plasm-ph].Google Scholar
Tsintsadze, N. L. & Tsintsadze, L. N.2015 arXiv:1.510.0878v1, [phys.plasma.ph].Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar
Zhang, B. & Harding, A. K. 2000 High magnetic field pulsars and magnetars: a unified picture. Astrophys. J. 535, L51–L54.CrossRefGoogle ScholarPubMed