Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:42:14.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Low-shear three-dimensional equilibria in a periodic cylinder

Part of: Focus on Fusion

Published online by Cambridge University Press:  20 February 2019

Erin Jaquiery  and
Wrick Sengupta Open the ORCID record for Wrick Sengupta [Opens in a new window]
Erin Jaquiery
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA Greenwich Academy, 200 N Maple Ave, Greenwich, CT 06830, USA
Wrick Sengupta*
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We carry out expansions of non-symmetric toroidal ideal magnetohydrodynamic (MHD) equilibria with nested flux surfaces about a periodic cylinder, in which physical quantities are periodic of period 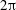$2\unicode[STIX]{x03C0}$ in the cylindrical angle 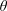$\unicode[STIX]{x1D703}$ and $z$. The cross-section of a flux surface at a constant toroidal angle is assumed to be approximately circular, and data are given on the cylindrical flux surface 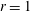$r=1$. Furthermore, we assume that the magnetic field lines are closed on the lowest-order flux surface, and the magnetic shear is relatively small. We extend earlier work in a flat torus by Weitzner (Phys. Plasmas, vol. 23, 2016, 062512) and demonstrate that a power series expansion can be carried out to all orders using magnetic flux as an expansion parameter. The cylindrical metric introduces certain new features to the expansions compared to the flat torus. However, the basic methodology of dealing with resonance singularities remains the same. The results, even though lacking convergence proofs, once again support the possibility of smooth, low-shear non-symmetric toroidal MHD equilibria.

Keywords

plasma confinementplasma devicesplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 1 , February 2019 , 905850115
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullaev, S. S. 2006 Construction of Mappings for Hamiltonian Systems and their Applications. Springer.Google Scholar
Arnol’d, V. I. 1963 Small denominators and problems of stability of motion in classical and celestial mechanics. Russian Math. Surveys 18 (6), 85–191.Google Scholar
Bauer, F., Betancourt, O. & Garabedian, P. 2012 A computational Method in Plasma Physics. Springer Science & Business Media.Google Scholar
Betancourt, O. & Garabedian, P. 1976 Equilibrium and stability code for a diffuse plasma. Proc. Natl Acad. Sci. USA 73 (4), 984–987.Google Scholar
Brakel, R., Anton, M., Baldzuhn, J., Burhenn, R., Erckmann, V., Fiedler, S., Geiger, J., Hartfuss, H. J., Heinrich, O., Hirsch, M. et al. & W7-AS Team, ECRH Group & NBI-Group 1997 Confinement in W7-AS and the role of radial electric field and magnetic shear. Plasma Phys. Control. Fusion 39 (12B), B273.Google Scholar
Brakel, R.& The W7-AS Team 2002 Electron energy transport in the presence of rational surfaces in the Wendelstein 7-AS stellarator. Nucl. Fusion 42 (7), 903.Google Scholar
Cary, J. R. & Littlejohn, R. G. 1983 Noncanonical hamiltonian mechanics and its application to magnetic field line flow. Ann. Phys. 151 (1), 1–34.Google Scholar
del Castillo-Negrete, D., Greene, J. M. & Morrison, P. J. 1996 Area preserving nontwist maps: periodic orbits and transition to chaos. Physica D 91 (1–2), 1–23.Google Scholar
Chierchia, L. & Gallavotti, G. 1982 Smooth prime integrals for quasi-integrable hamiltonian systems. Il Nuovo Cimento B 67 (2), 277–295.Google Scholar
Delshams, A. & De La Llave, R. 2000 KAM theory and a partial justification of greene’s criterion for nontwist maps. SIAM J. Math. Anal. 31 (6), 1235–1269.Google Scholar
Dewar, R. L. & Hudson, S. R. 1998 Stellarator symmetry. Physica D 112 (1), 275–280.Google Scholar
Firpo, M.-C. & Constantinescu, D. 2011 Study of the interplay between magnetic shear and resonances using hamiltonian models for the magnetic field lines. Phys. Plasmas 18 (3), 032506.Google Scholar
González-Enríquez, A., Haro, A. & De la Llave, R. 2014 Singularity Theory for Non-Twist KAM Tori, vol. 227. American Mathematical Society.Google Scholar
Grad, H. 1967 Toroidal containment of a plasma. Phys. Fluids 10 (1), 137–154.Google Scholar
Grad, H. 1973 Magnetofluid-dynamic spectrum and low shear stability. Proc. Natl Acad. Sci. USA 70 (12), 3277–3281.Google Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.Google Scholar
Hirsch, M., Baldzuhn, J., Beidler, C., Brakel, R., Burhenn, R., Dinklage, A., Ehmler, H., Endler, M., Erckmann, V., Feng, Y. et al. 2008 Major results from the stellarator Wendelstein 7-AS. Plasma Phys. Control. Fusion 50 (5), 053001.Google Scholar
Hirshman, S. P. & Whitson, J. C. 1983 Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553–3568.Google Scholar
Hudson, S. & Kraus, B. 2017 Three-dimensional magnetohydrodynamic equilibria with continuous magnetic fields. J. Plasma Phys. 83 (4), 715830403.Google Scholar
Kozlov, V. V. & Neishtadt, A. I. 2013 Dynamical Systems III. Springer Science & Business Media.Google Scholar
Kraus, B. F. & Hudson, S. R. 2017 Theory and discretization of ideal magnetohydrodynamic equilibria with fractal pressure profiles. Phys. Plasmas 24 (9), 092519.Google Scholar
Lichtenberg, A. J. & Lieberman, M. A. 1992 Regular and Chaotic Dynamics, Applied Mathematical Sciences, vol. 38.Google Scholar
Loizu, J., Hudson, S. R., Bhattacharjee, A., Lazerson, S. & Helander, P. 2015 Existence of three-dimensional ideal-magnetohydrodynamic equilibria with current sheets. Phys. Plasmas 22 (9), 090704.Google Scholar
Morrison, P. J. 2000 Magnetic field lines, hamiltonian dynamics, and nontwist systems. Phys. Plasmas 7 (6), 2279–2289.Google Scholar
Newcomb, W. A. 1959 Magnetic differential equations. Phys. Fluids 2 (4), 362–365.Google Scholar
Pyartli, A. S. 1969 Diophantine approximations on submanifolds of euclidean space. Funct. Anal. Applics. 3 (4), 303–306.Google Scholar
Sengupta, W. & Weitzner, H. 2018a Low-shear three-dimensional equilibria and vacuum magnetic fields with flux surfaces. J. Plasma Phys. (accepted). arXiv:1809.09225.Google Scholar
Sengupta, W. & Weitzner, H. 2018b Radial confinement of deeply trapped particles in a non-symmetric magnetohydrodynamic equilibrium. Phys. Plasmas 25 (2), 022506.Google Scholar
Sevryuk, M. B. 1995 KAM-stable hamiltonians. J. Dynam. Control Syst. 1 (3), 351–366.Google Scholar
Strauss, H. R. & Monticello, D. A. 1981 Limiting beta of stellarators with no net current. Phys. Fluids 24 (6), 1148–1155.Google Scholar
Weitzner, H. 2014 Ideal magnetohydrodynamic equilibrium in a non-symmetric topological torus. Phys. Plasmas 21 (2), 022515.Google Scholar
Weitzner, H. 2016 Expansions of non-symmetric toroidal magnetohydrodynamic equilibria. Phys. Plasmas 23 (6), 062512.Google Scholar
Wobig, H. 1987 Magnetic surfaces and localized perturbations in the Wendelstein VII-A stellarator. Z. Naturforsch. 42 (10), 1054–1066.Google Scholar