Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-29T13:19:26.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Ion-cyclotron modes in weakly relativistic plasmas

Published online by Cambridge University Press:  13 March 2009

Chandu Venugopal ,
P. J. Kurian  and
G. Renuka
Chandu Venugopal
Affiliation:
School of Pure and Applied Physics, Mahathma Gandhi University, Priyadarshini Hills, Kottayam 686 560, Kerala, India
P. J. Kurian
Affiliation:
School of Pure and Applied Physics, Mahathma Gandhi University, Priyadarshini Hills, Kottayam 686 560, Kerala, India
G. Renuka
Affiliation:
School of Pure and Applied Physics, Mahathma Gandhi University, Priyadarshini Hills, Kottayam 686 560, Kerala, India
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a dispersion relation for the perpendicular propagation of ioncyclotron waves around the ion gyrofrequency ω+ in a weaklu relaticistic anisotropic Maxwellian plasma. These waves, with wavelength greater than the ion Larmor radius rL+ (k⊥ rL+ < 1), propagate in a plasma characterized by large ion plasma frequencies (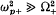). Using an ordering parameter ε, we separated out two dispersion relations, one of which is independent of the relativistic terms, while the other depends sensitively on them. The solutions of the former dispersion relation yield two modes: a low-frequency (LF) mode with a frequency ω < ω+ and a high-frequency (HF) mode with ω > ω+. The plasma is stable to the propagation of these modes. The latter dispersion relation yields a new LF mode in addition to the modes supported by the non-relativistic dispersion relation. The two LF modes can coalesce to make the plasma unstable. These results are also verified numerically using a standard root solver.

Type
Research Article
Information
Journal of Plasma Physics , Volume 51 , Issue 3 , June 1994 , pp. 371 - 379
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
Bornatici, M., Cano, R., DeBarbieri, O. & Engelmann, F. 1983 Nucl. Fusion 23, 1153.CrossRefGoogle Scholar
Cairns, R. A. 1991 Radio Frequency Heating of Plasmas. Adam Hilger.Google Scholar
Fuchs, V. & Bers, A. 1988 Phys. Fluids 31, 3702.CrossRefGoogle Scholar
Golovato, S. N., Brau, K., Casey, J., Gerver, M. J., Horne, S., Irby, J., Kesner, J., Lane, B., Machuzak, J., Myer, R., Post, R. S., Sevillano, E. & Wang, L. 1989 Phys. Fluids B 1, 651.CrossRefGoogle Scholar
Hutchinson, I. H. 1987 Principles of Plasma Diagnostics. Cambridge University Press.Google Scholar
Landau, R. W. & Cuperman, S. 1970 J. Plasma Phys. 4, 495.CrossRefGoogle Scholar
Landau, R. W. & Cuperman, S. 1971 J. Plasma Phys. 6, 495.CrossRefGoogle Scholar
Mourenas, D., Krasnosel'skikh, V. V. & Beghin, C. 1993 J. Geophys. Res. 98, 5855.CrossRefGoogle Scholar
Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. 1986 Numerical Recipes: The Art of Scientific Computing. Cambridge University Press.Google Scholar
Smith, G. R., Nevins, W. M. & Sharp, W. M. 1984 Phys. Fluids 27, 2120.CrossRefGoogle Scholar