Article contents
Inverse cascade and magnetic vortices in kinetic Alfvén-wave turbulence
Published online by Cambridge University Press: 08 March 2021
Abstract
A Hamiltonian two-field gyrofluid model for kinetic Alfvén waves (KAWs) in a magnetized electron–proton plasma, retaining ion finite-Larmor-radius corrections and parallel magnetic field fluctuations, is used to study the inverse cascades that develop when turbulence is randomly driven at sub-ion scales. In the directions perpendicular to the ambient field, the dynamics of the cascade turns out to be non-local and the ratio 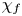 $\chi _f$ of the wave period to the characteristic nonlinear time at the driving scale affects some of its properties. For example, at small values of
$\chi _f$ of the wave period to the characteristic nonlinear time at the driving scale affects some of its properties. For example, at small values of  $\chi _f$, parametric decay instability of the modes driven by the forcing can develop, enhancing for a while inverse transfers. The balanced state, obtained at early time when the two counter-propagating waves are equally driven, also becomes unstable at small
$\chi _f$, parametric decay instability of the modes driven by the forcing can develop, enhancing for a while inverse transfers. The balanced state, obtained at early time when the two counter-propagating waves are equally driven, also becomes unstable at small 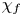 $\chi _f$, leading to an inverse cascade. For
$\chi _f$, leading to an inverse cascade. For 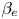 $\beta _e$ smaller than a few units, the cascade slows down when reaching the low-dispersion spectral range. For higher
$\beta _e$ smaller than a few units, the cascade slows down when reaching the low-dispersion spectral range. For higher 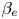 $\beta _e$, the ratio of the KAW to the Alfvén frequencies displays a local minimum. At the corresponding transverse wavenumber, a condensate is formed, and the cascade towards larger scales is then inhibited. Depending on the parameters, a parallel inverse cascade can develop, enhancing the elongation of the ion-scale magnetic vortices that generically form.
$\beta _e$, the ratio of the KAW to the Alfvén frequencies displays a local minimum. At the corresponding transverse wavenumber, a condensate is formed, and the cascade towards larger scales is then inhibited. Depending on the parameters, a parallel inverse cascade can develop, enhancing the elongation of the ion-scale magnetic vortices that generically form.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 9
- Cited by



