1 Introduction
The construction cost of stellarators is dominated by the manufacturing and assembly process of the primary coil system, which produces the ‘magnetic cage’ in which the plasma is later confined. Budget and schedule of the whole project strongly depends on the construction tolerances which are derived from a perturbation analysis after the primary coil system is designed. Unfortunately, the construction of recent stellarator experiments like Wendelstein 7-X (W7-X) and the National Compact Stellarator Experiment (NCSX) were negatively influenced by their low construction tolerances, which led, in the case of NCSX, to the cancellation of the whole project (Orbach Reference Orbach2008). A method that increases construction tolerances without compromising the performance of the magnetic field would be highly beneficial.
We investigated the problem by integrating a perturbation analysis into the optimization loop of ONSET (Drevlak Reference Drevlak1998b), a nonlinear coil optimization suite. Instead of optimizing a single coil configuration, the average of a cloud of coil configurations is optimized. Each element of the cloud is a perturbation of the coil set at the cloud’s centre. The cloud is characterized by the number of samples 
$N$ (perturbations) and its size is defined by the average perturbation amplitude. In our earlier work (Lobsien, Drevlak & Pedersen Reference Lobsien, Drevlak and Pedersen2018) that concentrated on coil configurations for the original W7-X plasma boundary the average perturbation amplitude was kept fixed at 2 mm while the number of samples 
$N$ was varied between 1 and 8000. Each perturbation was two-dimensional and displaced the coil set across its winding surface. For one sample this reduces to the non-stochastic case of classic stellarator coil optimization called the reference case. The stochastically optimized coil configurations were able to reproduce the target magnetic field more accurately with a local maximum field error of 6.08 % and an average field error of 1.56 % while we observed an increased resilience with respect to the objective function 
$f$. A subsequent derivation of reactor relevant 
$\langle \unicode[STIX]{x1D6FD}\rangle =5\,\%$ equilibria allowed us to analyse the performance of the coil configurations with respect to the criteria that originally led to the shape of the plasma boundary of W7-X. The investigation revealed that stochastic stellarator coil optimization outperforms classic stellarator coil optimization irrespective of the sample size (Lobsien et al. Reference Lobsien, Drevlak, Jenko, Maurer, Navarro, Nührenberg, Pedersen, Smith and Yuriy2020).
In this manuscript, we build on the results obtained in Lobsien et al. (Reference Lobsien, Drevlak and Pedersen2018) and study the effects of stochastic stellarator coil optimization with three-dimensional (3-D) perturbations on a different coil design process for the original W7-X plasma boundary. First, we solely concentrate on the field error, then implement the geometric and vacuum magnetic field properties in two subsequent phases. The number of samples is increased to 
$N=20\,000$ while we test three different average perturbation amplitudes 0 mm, 2 mm and 5 mm. The case with a cloud size of 0 mm reduces again to the case of classic stellarator coil optimization, called the reference case.
We also test here the effect of the nonlinear coil optimization tool FOCUS (Zhu et al. Reference Zhu, Hudson, Song and Wan2017) to reduce the field error in the first phase of the design process. ONSET is then used to implement the geometric constraints and adjust the properties of the vacuum magnetic field. Following this procedure, we are able to compare the performance of two nonlinear coil optimization tools. Their differences with respect to the objective function 
$f$ are described in § 2 together with the perturbation technique that is used in the stochastic version of ONSET. A detailed description of the design process closes the methodology. In § 3 we investigate the development of the field error during the design process and analyse the final fitness of the coil configurations. Their robustness with respect to the objective function 
$f$ is investigated by a perturbation analysis. Lastly, we visualize the final coil configurations and conclude the investigation.
2 Methodology
The task of designing a stellarator coil system can be seen as the second step in the process of designing a stellarator. A given plasma boundary uniquely defines the vacuum magnetic field in its interior and, together with a pressure and current profile, the finite-
$\unicode[STIX]{x1D6FD}$ effects when a plasma pressure is applied. Intuitively, one first tries to find the optimal plasma shape that performs best with respect to predefined performance criteria like magnetohydrodynamic (MHD) stability, energy and particle transport, and fast particle confinement. In the second step, one aims to reproduce the desired magnetic field with a finite set of coils. The magnetic field, which later confines the plasma, is the crucial element in this scenario by building the bridge between stellarator and coil optimization.
Deriving external currents that produce a given magnetic field is an inverse problem that is ill posed, but can be solved linearly on a surface outside the plasma boundary with NESCOIL (Merkel Reference Merkel1987) or its successor REGCOIL (Landreman Reference Landreman2017) that allows different regularization schemes. The result is a continuous and smooth current distribution on the winding surface which can be discretized into a finite set of filaments that describe a coil set. The magnetic field of the coil set can be further improved with codes such as ONSET (Drevlak Reference Drevlak1998b), COILOPT (Strickler, Berry & Hirshman Reference Strickler, Berry and Hirshman2002), COILOPT
$^{++}$ (Brown et al. Reference Brown, Breslau, Gates, Pomphrey and Zolfaghari2015) and FOCUS (Zhu et al. Reference Zhu, Hudson, Song and Wan2017) which translate the problem into the minimization of a nonlinear objective function 
$f$. It consists of the parametrization 
$h$ and the penalty function 
$g$, i.e. 
$f=g\circ h$.
ONSET and FOCUS show substantial differences in the choice of the coil parametrization (§ 2.1), the quality criteria that define the penalty function (§ 2.2) and the optimizer that minimizes the objective function 
$f$. ONSET has several optimizers, but we use Brent’s method (Gegenfurtner Reference Gegenfurtner1992) which approximates the Hessian of 
$f$ in an iterative process and optimizes along its principal axes. FOCUS, on the other hand, computes the gradient and Hessian (Zhu et al. Reference Zhu, Hudson, Song and Wan2018b) of 
$f$ analytically. FOCUS also has several optimizers to minimize the objective function 
$f$, but in this study, we will mainly use the conjugate gradient method. ONSET has the ability to optimize a coil configuration stochastically, which perturbs the coil configuration to create a sample cloud. The technique is explained in § 2.3. The values of the weight constants 
$\unicode[STIX]{x1D714}_{i}$ define the coil design process (§ 2.4), which is the path we chose to solve the coil optimization problem defined as
$$\begin{eqnarray}\min _{x\in \mathbb{R}^{n}}f(x),\end{eqnarray}$$ where 
$x\in \mathbb{R}^{n}$ is the set of parameters describing the coil set. The objective function
$$\begin{eqnarray}f:\mathbb{R}^{n}\rightarrow \mathbb{R},\quad f(x)=(g\circ h)(x)\end{eqnarray}$$ consists of a parametrization 
$h:\mathbb{R}^{n}\rightarrow \mathbb{R}^{3S}$ which maps the set of parameters to a set of 
$S$ filament points that describe the coil set in the 3-D Euclidean space. Subsequently, the penalty function 
$g:\mathbb{R}^{3S}\rightarrow \mathbb{R}$ calculates the magnetic field with the Biot–Savart formula and measures the difference between the magnetic field produced by the coils and the target magnetic field defined by the shape of the plasma boundary. In detail, it calculates the quality criteria, which are compared to the design values of the target magnetic field while simultaneously assuring that the shape of the coil set is feasible for construction.
2.1 Parametrization
Coil sets are parametrized differently in FOCUS and ONSET. FOCUS uses a three-dimensional Fourier representation of the coil set, where each spatial coordinate is represented by
$$\begin{eqnarray}x^{i}(t)=x_{c,0}^{j}+\mathop{\sum }_{n=1}^{N_{F}}[x_{c,n}^{j}\cos (nt)+x_{s,n}^{j}\sin (nt)]\quad \text{with }t\in [0,2\unicode[STIX]{x03C0}]\end{eqnarray}$$ and 
$j=\{1,2,3\}$. This parametrization avoids the necessity of a winding surface. In total, the number of parameters defining a single coil is 
$3\times (2N_{F}+1)$.
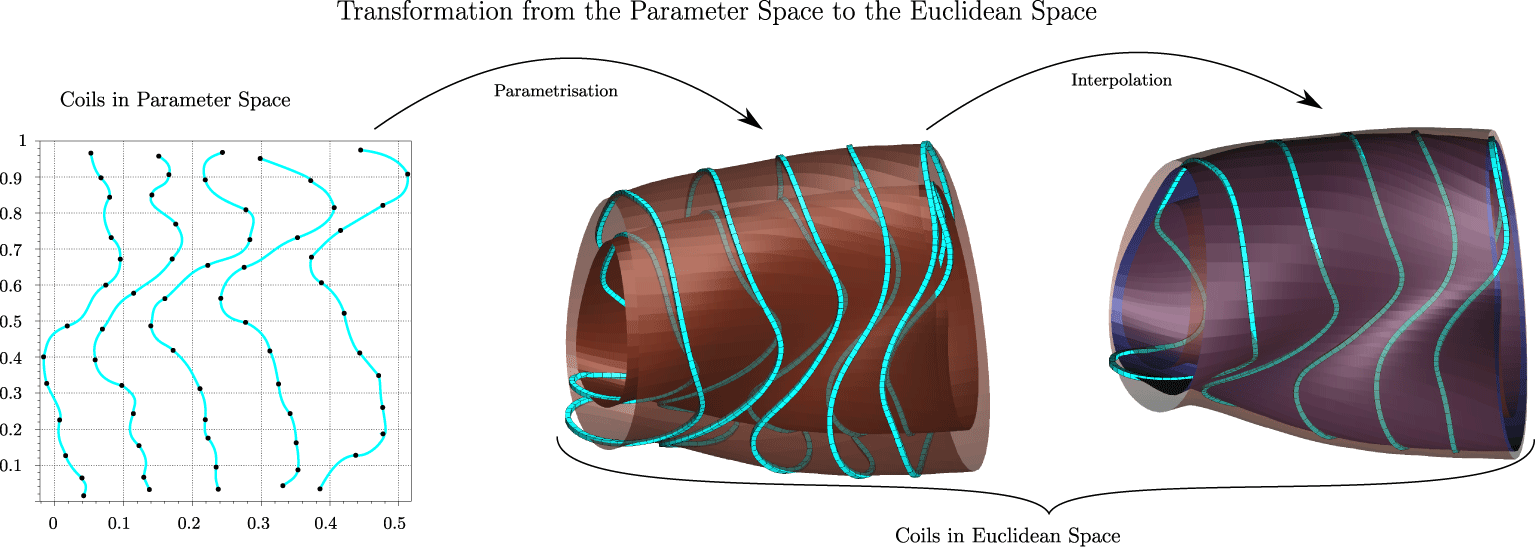
The winding surface is an essential element of the parametrization we chose in ONSET. Its two parts are visualized in figure 1. Each coil consists of 
$2\times N_{O}$ parameters describing a cubic periodic spline in the two-dimensional plane. The splines are then mapped by 
$h$ onto two limiting surfaces. Additional 
$N_{O}$ parameters then interpolate the winding surface between two limiting surfaces. The interpolation uses the arc tangent such that the winding surface can never reach the limiting surfaces. Full three-dimensional flexibility of the coil set can be achieved when the parametrization is extended such that each coil has its own set of parameters that interpolate the winding surface between the two limiting surfaces. This way, each coil is attached to its own winding surface and can be displaced independently perpendicular to it. Such a flexibility is comparable to that available in FOCUS. The number of parameters then yields 
$3\times N_{O}$ per coil.
Figure 1. The parametrization used in ONSET.
We choose 
$N_{O}=13$ and 
$N_{F}=6$ such that ONSET and FOCUS use the same number of parameters per coil.
2.2 Penalty function
In order to compute the value of the penalty function 
$g$, the magnetic field produced by the coil set is computed. Subsequently, characteristics of that magnetic field are derived called quality criteria. The analytic function that maps the quality criteria to the penalty value in 
$\mathbb{R}$ is the last part of the calculation of the penalty function and is defined by
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D714}_{i}(q_{i}(x)-q_{i}^{\text{design}})^{2}.\end{eqnarray}$$ The value of the quality criterion 
$q_{i}(x)$ is subtracted from its design value 
$q_{i}^{\text{design}}$ and yields, factorized by its weight constant 
$\unicode[STIX]{x1D714}_{i}$, the specific contribution to the penalty function. The change of the weight constants 
$\unicode[STIX]{x1D714}_{i}$ defines the coil design process and is explained in § 2.4. The target plasma boundary uniquely defines the target vacuum magnetic field from which the design values 
$q_{i}^{\text{design}}$ are derived prior the optimization.
The most dominant quality criterion is the field error evaluated by computing 
$\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}$, where 
$\boldsymbol{B}$ is the vector of the magnetic field produced by the coils and 
$\boldsymbol{n}$ is the normal on the target plasma boundary. In general, 
$\boldsymbol{B}$ may include internal plasma currents, which were absent in the optimization of W7-X. FOCUS minimizes the average squared field error
$$\begin{eqnarray}q_{\text{ase}}(x)=\int _{A}\frac{1}{2}(\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n})^{2}\,\text{d}A,\end{eqnarray}$$ where 
$A$ is the area of the plasma boundary. ONSET uses two different measures for the normalized field error
$$\begin{eqnarray}q_{\text{le}}(x)=\frac{|\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{n}|}{|\boldsymbol{B}|}.\end{eqnarray}$$ The maximum local field error 
$\max q_{\text{le}}$ and the average global field error
$$\begin{eqnarray}q_{\text{ae}}(x)=\frac{\displaystyle \int _{A}q_{\text{le}}\,\text{d}A}{A}.\end{eqnarray}$$ In ONSET, one can fully control the shape of the coil set by geometric constraints. The material used for the coils defines the finite extent of the coils, which sets the minimal clearance between adjacent coils. This design process uses two limiting surfaces which guarantee that the coils do not get too close or too far away from the plasma boundary. The finite extent of the coils also defines the maximal allowed coil curvature. Its computation in ONSET follows 
$\unicode[STIX]{x1D705}=1/R$, where 
$R$ is the smallest radius of curvature for a given coil. Unnecessary undulations are penalized by a second curvature, which is a weighted variant of the first curvature described in Drevlak (Reference Drevlak1998a). Ultimately, crossing points are penalized. These criteria define the geometric properties absolute necessary for the construction of the W7-X central coil system.
ONSET has additionally the capability to optimize properties of the vacuum magnetic field by following magnetic field lines and calculating magnetic flux surfaces. The properties and their calculation are explained in more detail in Drevlak (Reference Drevlak1998a) and briefly summarized here:
(i) The position of the magnetic axis is determined by finding the fixed point of the field line map and two positions of the magnetic axis at the beginning and at the end of the half-module are evaluated.
(ii) The difference between the magnetic field strength on the axis at the start and at the end of the half-module is referred to as the magnetic mirror. It is normalized to the sum of the two magnetic field strength values.
(iii) The value of the rotational transform
$\unicode[STIX]{x1D704}$ on axis and the corresponding shear in radial direction, that are necessary for confinement, are determined. The shear is computed by taking the difference of $\unicode[STIX]{x1D704}$ on axis and $\unicode[STIX]{x1D704}$ 0.2 m off axis at the beginning of the half-module at $z=0$.(iv) The magnetic well (hill) is defined as the normalized difference of the specific volume of two well-separated magnetic surfaces (including the magnetic axis). The specific volume is defined as
$\lim _{N\rightarrow \infty }(1/N)\int _{N}(\text{d}l/B)=\text{d}V/\text{d}\unicode[STIX]{x1D6F9}$, where $\unicode[STIX]{x1D6F9}$ is the toroidal magnetic flux.(v) The Fourier coefficients of inner flux surfaces can be computed and optimized towards the coefficients of the corresponding surfaces of the target magnetic field. They are derived in PEST coordinates (Grimm, Greene & Johnson Reference Grimm, Greene, Johnson and Killeen1976) and we chose the
$R_{mn}$ and $Z_{mn}$ of a flux surface slightly inside the plasma boundary.
FOCUS has less control of the coil geometry than ONSET despite having penalty functions over the coil length, coil-to-coil separation, coil–plasma separation and coil curvature. To use analytic derivatives, FOCUS employs integrated formulas for these engineering constraints. The primary constraints used in this study are the coil length and coil curvature. The penalty on the coil length is
$$\begin{eqnarray}q_{L}(x)=\frac{1}{N_{C}}\mathop{\sum }_{i=1}^{N_{C}}\frac{1}{2}\frac{(l_{i}(x)-l_{i,o}(x))}{l_{i,o}(x)},\quad \text{where }l_{i}(x)=\int _{0}^{2\unicode[STIX]{x03C0}}|x_{i}^{\prime }|\,\text{d}t\end{eqnarray}$$ is the length of the 
$i$th coil, 
$l_{i,o}$ is the target length and 
$N_{C}$ is the number of coils. It has the disadvantage that if choosing 
$l_{i,o}$ too low, one can perfectly approximate the plasma boundary but cannot control the geometric properties of the coil. Choosing 
$l_{i,o}$ too high, one obtains values of the field error that are too large. The introduction of a penalty on the curvature improved the shape of the coil sets but could not completely avoid the violation of the second curvature and the coil-to-coil clearance used in ONSET. Compared to ONSET, the squared curvature was optimized. Due to technical limitations, a version of FOCUS that could use the curvature and coil-to-coil constraint was not available during our computations.
2.2.1 Remark
Both ONSET and FOCUS have the ability to optimize additional physics properties. We list them here to give a full overview of the characteristics of the two coil optimization suites.
ONSET:
(I) Following magnetic field lines, ONSET can check the existence of magnetic flux surface.
(II) On a flux surface ONSET can also compute:
(i) The Fourier coefficients of the magnetic field
$H_{mn}$ in PEST coordinates.(ii) Epsilon effective
$\unicode[STIX]{x1D716}_{\text{eff}}$.
(III) ONSET can detect the fixed point of magnetic islands and optimize their width by computing their residual (Greene Reference Greene1968).
(IV) ONSET has the ability to do equilibrium calculations with VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983) such that all performance criteria available in the stellarator optimization suite ROSE (Drevlak et al. Reference Drevlak, Beidler, Geiger, Helander and Turkin2018) can be optimized.
(V) A NESCOIL calculation can be invoked to compute the current distribution needed to eliminate the residual field error. This is useful for optimizing systems of simple primary field coils (toroidal field component in a mixed-topology coil system) so as to minimize the burden on a saddle coil or permanent-magnet solution providing the rotational transform.
ONSET and FOCUS can optimize the current that flows through the coils. In this manuscript, all coils were equipped with an equal current of 1.45 MA.
FOCUS:
(I) FOCUS can detect magnetic islands and optimize the island width (Zhu et al. Reference Zhu, Hudson, Lazerson, Song and Wan2018a).
(II) FOCUS can optimize the quasi-symmetry of the configuration (Zhu et al. Reference Zhu, Hudson, Lazerson, Song and Wan2018a).
We did not optimize any of these properties because their investigation would be out of the scope of this manuscript.
2.3 Perturbation of the coil set
Stochastic coil optimization extends the optimization of a single coil configuration (cf. (2.1)) to the optimization of a cloud of coil configurations
$$\begin{eqnarray}\min _{x\in \mathbb{R}^{n}}F_{N}(x).\end{eqnarray}$$ The cloud is characterized by the number of samples 
$N$. Each element of the cloud is a perturbation of the original coil set at the cloud’s centre. A perturbation of the coil configuration can be intuitively achieved by perturbing the set of parameters that define the coil set. This leads to the objective function
$$\begin{eqnarray}F_{N}(x):=\frac{1}{N+1}\mathop{\sum }_{i=0}^{N}f(\unicode[STIX]{x1D709}_{i}(x))+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}=\frac{1}{N+1}\mathop{\sum }_{i=0}^{N}(g\circ h\circ \unicode[STIX]{x1D709}_{i})(x)+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D709}_{0}(x)=x_{0}$ is the original parameter set and 
$\{\unicode[STIX]{x1D709}_{i}(x)\}_{i=1,\ldots ,N}$ is the set of perturbed parameter sets which have a Gaussian distribution around the cloud’s centre. The last term after the sum 
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}$ is a penalty on the standard deviation 
$\unicode[STIX]{x1D70E}$ of the penalty value distribution of one sample cloud. It is a tool of risk averse programming and is intended to increase the robustness with respect to 
$f$. In the previous coil optimization study (Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018), we only perturbed the parameters that deform the coil set across its winding surface. Here, we perturb all of the input parameters and assure that the deviation of the winding surface itself has the same magnitude as the deviation across the winding surface. The perturbation of the parameters has the disadvantage that the outcome of the displacement is hard to control and strongly depends on the parametrization.
We describe the extent of the cloud of samples in physical units of mm by the average perturbation amplitude. It is defined by
$$\begin{eqnarray}\frac{1}{N}\cdot \frac{1}{500}\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{500}\overline{p_{ij}p_{ij}^{u}},\end{eqnarray}$$ where 
$\overline{p_{ij}p_{ij}^{u}}$ is the distance between the perturbed 
$p_{ij}$ and unperturbed 
$p_{ij}^{u}$ filament points. The sum goes over all the 500 filament points that describe a coil set and over all the coil sets in the cloud except the unperturbed one.
2.4 Design sequence
The coil design process is divided into three phases. The first phase solely concentrates on the field error, the next phase then targets the geometric properties and, last but not least, the properties of the vacuum magnetic field are optimized. Each phase is defined by the corresponding values of the weight constants 
$\unicode[STIX]{x1D714}_{i}$ which are shown in table 1.
Table 1. Design sequence in ONSET: 
$q_{i}^{\text{design}}/\unicode[STIX]{x1D714}_{i}$.
The optimization of the field error consists of multiple adjustments that shift the outer limiting surface further away to find the optimal coil-to-plasma distance. Similarly, we start the optimization phase with fewer points per coil to slowly increase the geometric freedom of the coil set while the weights for the field errors and the standard deviation 
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}}$ are kept fixed throughout the whole design process.
The second design phase focuses on controlling and improving the geometric properties while keeping the weights on the field error fixed. The whole process adjusts the weights of the coil-to-coil clearance and the two curvatures to their final values with the overall aim of not increasing the value of the field error. This may not always be possible. In some cases, large kinks and/or self-intersections of the coils appear, and the code can get stuck with these unacceptable features, even after the geometric properties have been included in the penalty function in phase II. We find that this can be avoided by either using stochastic optimization already in phase I, or switching to phase II early, i.e. before having completed phase I. This is another indication that the optimization space has many local minima in which the optimizer can get stuck. The coil sets first optimized with FOCUS enter the design sequence with ONSET at phase II.
After the shape of the coil set meets the geometric constraints, the coil design process concludes with the optimization of properties of the vacuum magnetic field. The last design phase usually concentrates first on the magnetic axis, iota profile and the magnetic mirror and well, and then it concentrates on the Fourier coefficients of an inner flux surface. All the design values 
$q_{i}^{\text{design}}$ were previously deduced from the target vacuum magnetic field which corresponds to the original W7-X plasma boundary. The boundary was first introduced in Nührenberg & Zille (Reference Nührenberg and Zille1988), but the high-mirror configuration we are using is better described in Nührenberg (Reference Nührenberg1996).
The design sequence described here is slightly different from the one used in the previous study (Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018). There, the geometric properties are optimized simultaneously to the field error such that phases I and II are combined into a single phase. In its concluding phase, the weights of the vacuum field properties are reduced and the outer limiting surface is kept fixed at 
$+75~\text{cm}$.
3 Results
In this section, we investigate the effects of stochastic stellarator coil optimization using 3-D perturbations. We follow the coil design process described in § 2.4 that consists of three phases. Two coil configurations are optimized using the stochastic version of ONSET with average perturbation amplitudes of 2 mm and 5 mm. In both cases, the cloud consists of 20 000 samples. The investigation includes two reference cases: one reference case passes the whole design process with the single sample version of ONSET, the other reference case is first optimized with FOCUS and then enters the design process with the single sample version of ONSET at phase II. We refer to them as reference cases ONSET and HYBRID. In order to be consistent with the first design phase of the previous design process (Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018), the two stochastic cases and the reference case ONSET use a single winding surface in phases I and II while in phase III they use the extended parametrization where each coil is attached to its own winding surface. The perturbation used in the stochastic optimization always uses the current set of parameters that describe the coil set. The reference case HYBRID uses the extended parametrization of ONSET throughout phases II and III.
3.1 Comparison after design phase I
In table 2 we list the maximal and average field error of the coil configurations after the completion of the first design phase.
Table 2. Values of the maximal and average field error after design phase I.
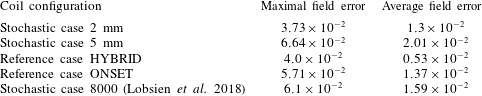
The reference case HYBRID reaches by far the lowest average field error, which is directly targeted through the average squared error in its objective function. Not directly covered is the maximal field error, which is slightly higher than the value of the stochastic case 2 mm. The reduced coil flexibility of the stochastic case 2 mm in phase I inhibited a further reduction of the field error but is not responsible for the large difference in the average field error values compared to the reference case HYBRID.
In the previous study (Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018), the first design phase concentrated on the field error and the geometric properties simultaneously. The lowest field error values (after first design phase) were achieved by the stochastic case 8000. Compared to these values, the stochastic case 2 mm could reduce the maximal field error by 40 % and the average field error by 15 %. This shows that in principle geometric constraints inhibit the optimization of the field error because they restrict the shape of the coil. The stochastic case 5 mm occupies the lowest rank, which shows that an increase of the average perturbation amplitude negatively influences the optimization of the field error similar to geometric constraints.
We compare the speed and the corresponding efficiency of the three optimization approaches by the number of evaluations of their individual objective functions assuming that the evaluations take a similar amount of time. In the stochastic optimization this does not include the 20 000 samples, since their computation is parallelized, which only marginal contributes to the evaluation time due to the communication between the processes. FOCUS only needed 300 evaluations of its objective function 
$f$ to arrive at that very low minimum. The stochastic case 5 mm needed 5000 evaluations of its objective function 
$F_{N}$, corresponding to 
$10^{8}$ evaluations of 
$f$, to converge and the stochastic case 2 mm needed 28 000 evaluations of 
$F_{N}$ (
$5.6\times 10^{8}$ evaluations of 
$f$) to arrive at a slightly worse performing minimum. This is two orders of magnitude more evaluations of the objective function, which shows the advantage of optimizing with derivatives.
3.2 Comparison after design phase II
The design phase II fully concentrates on implementing the geometric properties of the coil configurations. This was not possible for the reference case ONSET because the geometric penalties used in the design process were not able to repair the kink in coil number 1 counting from the left. We visualize the reference case ONSET together with both stochastic coil cases in figure 2. Both have a much smoother coil shape, which shows that the technique of stochastic coil optimization works as a geometric constraint and reduces the maximal and average coil curvatures.
The development of the field error in phase II is especially interesting, because geometric constraints are not necessary to obtain an optimal approximation of the desired magnetic field. We visualize the values of the two stochastic cases and the reference case HYBRID in table 3. The relatively low field errors increased in the stochastic case 2 mm and in the reference case HYBRID, which shows again that geometric constraints negatively influence the optimization of the field error. But the relatively high field errors of the stochastic case 5 mm decreased. This does not contradict the previous statement because, in principle, geometric constraints just change the landscape of the optimization space. An optimization which was previously halted by the increased average perturbation amplitude can continue to minimize the field error if the change of the landscape includes a beneficial change of the local minimum. The increase in field error indicates that geometric constraints set the lower boundary of the field error. We point out that the stochastic case 2 mm still has lower field error values than the stochastic case 8000 (cf. table 2) which shows the advantage of adding shape penalties at a later step in the design process when using stochastic optimization.
Figure 2. The stochastic case 2 mm is situated (a), the reference case ONSET is situated in (b) and the stochastic case 5 mm is situated (c).
FOCUS can reduce the field error to values much lower than shown in table 2 by increasing the length of the coil. It gives the coil more freedom to take shape and thus better approximate the magnetic field. Unfortunately, the field error later increased again in phase II to values higher than shown in table 3. This shows that, for a coil configuration with our desired geometric properties, the average coil length of 8.5 m is optimal to approximate the magnetic field of the W7-X configuration. This is confirmed by the average coil length of the two stochastic cases.
Figure 3. Perturbation analysis of the two stochastic cases and the reference case HYBRID. All the coil sets were perturbed 200 000 times by changing the input parameters. The vertical dashed line shows the penalty value of the unperturbed coil configuration.
Table 3. Values of the maximal and average field errors after design phase II.
The absence of a penalty on the coil curvature in FOCUS could initially, in phase I, also reduce the field error to values lower than shown in table 2, but they increased again in phase II to values higher than shown in table 3. The situation was not as fatal as for the reference case ONSET but it shows that the geometric constraints can be beneficial and can prevent the optimizer from entering local minima that are far from the global minimum.
3.3 Comparison after design phase III
In this section we investigate the fitness and robustness of the two stochastic cases together with the reference case HYBRID after they completed the coil design process. The total fitness is represented by the penalty value and the robustness is visualized by the penalty value histograms obtained by a perturbation analysis. Each coil configuration is perturbed 200 000 times, with an average perturbation amplitude of 2 mm. Their penalty value histogram together with the penalty value of the unperturbed coil configuration is shown in figure 3.
The stochastic case 5 mm has the lowest penalty value after the completion of the design process, which needed 58 000 evaluations of the objective function 
$F_{N}$ (
$1.16\times 10^{9}$ evaluations of 
$f$). Closely behind follows the reference case HYBRID, which needed 86 000 evaluations of the objective function 
$f$ to complete phases II and III. The stochastic case 2 mm arrives at a slightly higher penalty value but needed only 69 000 evaluations of 
$F_{N}$ (
$1.38\times 10^{9}$ evaluations of 
$f$) to conclude the design process. This means that the larger the average perturbation amplitude, the fewer evaluations are necessary to converge. Figure 3 additionally shows that a larger average perturbation amplitude does not necessarily lead to a lower performance. The penalty value histogram of the stochastic case 2 mm shows the highest peak and the smallest width. Thus, the coil configuration is most robust with respect to the objective function 
$f$, which is closely followed by the stochastic case 5 mm. The lowest robustness with respect to 
$f$ shows the reference case HYBRID with a noticeable difference from the stochastic cases. This was expected because it was not optimized for that.
Table 4. Values of the maximal and average field errors after design phase III.
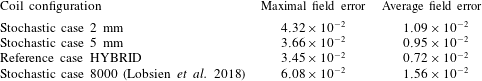
We visualize the field errors after the completion of the design process in table 4. The penalties on the properties of the vacuum magnetic field and the increased flexibility through the extended parametrization in phase III could further reduce the field error of the stochastic cases, which means that the previous design step ended again in a local minimum. The design process of the reference case HYBRID took a completely different path, because it started with a very low average field error which increased during the design process and only the maximum field error slightly decreased. During phases II and III, coil configurations that used a stronger penalty on the coil length in FOCUS could not decrease their final field error to values lower than shown in table 4, whereas a weaker penalty led to field error values as much higher than shown in table 4. All of the coil configurations discussed here have reached lower field error values than the best results of previous W7-X design studies (Drevlak Reference Drevlak1998a; Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018).
3.4 Picture of the coil configurations
In figure 4 we visualize the coil configuration of the two stochastic cases and the reference case HYBRID after they completed the coil design process. Although having similar fitnesses, their coil shapes are quite different and only coincide at the diagonal section on the inboard side (cf. figure 4b).
Figure 4. The final coil configurations of the reference case HYBRID together with two stochastic cases are shown from both sides.
4 Discussion and conclusion
We investigated the effects of 3-D stochastic stellarator coil optimization and followed a coil design process for the original Wendelstein 7-X plasma boundary that focused on the reduction of the field error. The design process consists of three phases: field error, geometric properties and properties of the vacuum magnetic field. The stochastic optimization is used with average perturbation amplitudes of 5 mm, 2 mm and 0 mm, with the latter case reducing to the single sample version of ONSET, i.e. the reference case ONSET. Unfortunately, the reference case ONSET could not finish the design process successfully, which shows that certain geometric properties are necessary to prevent the optimizer from entering a local minimum that leads to unpractical coil shapes. The stochastic case 5 mm completed the design process and reached the lowest penalty value of exactly 2 and consequently the best fitness. Its field errors are 3.66 % maximal and 0.95 % on average and, excepting phase II, they reduced over the course of the design process. With the aim of putting our results into a broader perspective, we used the FOCUS code to reduce the field error in phase I and then finished the design process with the single sample version of ONSET. This reference case HYBRID concluded with a slightly higher penalty value of 2.07 but lower field error values of 3.45 % maximal and 0.72 % on average. In contrast to the two stochastic cases, the field error increased during the optimization of the geometric and vacuum magnetic field properties (phases II and III). This is consistent with but does not prove that the field error values obtained here are close to a global field error minimum of a coil configuration that meets the geometric constraints necessary to build Wendelstein 7-X. Comparing the results to our previous design study (Lobsien et al. Reference Lobsien, Drevlak and Pedersen2018) shows that the absence of most of the geometric constraints in the first phase of the design process in combination with an increased sample size and fully 3-D perturbations yielded lower field error values. We conclude that geometric constraints are responsible for the creation of local less performing minima in which the optimizer got stuck.
We have shown in this paper that the enhanced robustness in our previous study can be extended to three-dimensional perturbations facilitated by the penalty on the standard deviation 
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}$. We also compared the penalty value histograms for coil sets designed with the stochastic version of ONSET and ones designed with FOCUS first and then ONSET. The robustness of the reference case HYBRID with respect to the objective function is noticeably lower than the two stochastic cases. This is consistent with our previous finding that the stochastic optimization approach tends to improve robustness, although stochastic optimizations with FOCUS in the future will shed more light on this. The FOCUS code uses nearly two orders of magnitude fewer evaluations for similar results in phase I.
We also found that, when optimizing with FOCUS in phase I and with ONSET for phase II and III without stochastic optimization, results are improved significantly over previous non-stochastic optimizations, but still perform less well and are significantly less robust than the best stochastic optimization results.
4.1 Remark on geometric constraints
A coil configuration needs to fulfil certain geometric properties such that its design can be realized during a subsequent construction. The corresponding geometric constraints used during the optimization have a strong effect on the optimization space. Omitting them completely leads to a reduction of the field error, but allows the optimization to arrive at a non-optimal minimum that terminates the design process. From testing stochastic stellarator coil optimization without geometric constraints, we can say that a penalty on the coil curvature is necessary to prevent such a situation, but previous studies have shown that a penalty that is too large has a negative effect on the field error. The study conducted in this manuscript shows that one is able to fix the geometric properties at a later step in the design process, when the coil configuration was optimized with only a small penalty on the curvature, without dramatically increasing the field error. To summarize, geometric constraints are necessary to prevent the optimizer from getting stuck in non-optimal minima, but chosen too high can halt the whole optimization process.
Acknowledgements
The authors thank L. Rudischhauser and D. Böckenhoff for fruitful discussions and support. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programs 2014–2018 and 2019–2020 under grant agreement no. 633053. The views and options expressed herein do not necessarily reflect those of the European Commission. This work was supported by a grant from the Simons Foundation/SFARI (560651, AB). The simulations presented in this work were performed at the HYDRA and COBRA HPC system at the Max Planck Computing and Data Facility (MPCDF), Germany and at the MARCONI HPC system at CINECA, Italy.
Open access
