Article contents
Impact of wiggler magnetic field on wakefield generation and electron acceleration by Gaussian, super-Gaussian and Bessel–Gaussian laser pulses propagating in collisionless plasma
Published online by Cambridge University Press: 02 March 2023
Abstract
In this research, the process of electron acceleration and wakefield generation by Gaussian-like (GL), super-Gaussian (SG) and Bessel–Gaussian (BG) laser pulses through cold collisionless plasma in the presence of a planar magnetostatic wiggler are studied. Three different types of laser spatial profiles, GL, SG and BG, are considered. Additionally, using the hydrodynamics fluid equations, Maxwell's equations as well as the perturbation technique for GL, SG and BG laser pulses in the weakly nonlinear regime and in the presence of a planar magnetostatic wiggler, governing equations for analysing the laser wakefield and electron acceleration have been derived and compared correspondingly. In addition, the effect of some important factors, including the wiggler field strengths, laser intensity, pulse length, plasma electron density and laser frequency on the wakefield and the electron energy gain, have been investigated. Numerical results show that enhancing the wiggler magnetic field results in an increase in the amplitude of the wakefield. Furthermore, it is observed that in comparison with the wakefield amplitude excited by SG and GL laser pulses, the amplitude of the wakefield excited by BG laser pulse is larger when the wiggler field is enhanced. Moreover, it is realized that the type of the laser profile, selected laser parameters and wiggler magnetic field are the most decisive and effective factors in the wakefield amplitude and shape of wakefield generation through cold collisionless plasma. Also, it is seen that as the pulse length declines, the amplitude of the wakefield increases, and correspondingly the resonance positions shift to higher ${({\varOmega _w}/{\varOmega _p})_{max}}$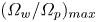 values.
values.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
A correction has been issued for this article:
- 18
- Cited by
Linked content
Please note a has been issued for this article.



