1 Introduction
Ion motion in a magnetized collisionless shock front is affected by macroscopic large-scale weakly varying and microscopic small-scale fast-varying magnetic and electric fields. Low Mach number low-
![]() $\unicode[STIX]{x1D6FD}$
shocks are nearly one-dimensional and stationary (Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Formisano and Neugebauer1975; Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Gosling, Bame, Paschmann, Parks, Anderson, Anderson and Gurnett1980; Russell et al.
Reference Russell, Hoppe, Livesey and Gosling1982; Mellott & Greenstadt Reference Mellott and Greenstadt1984; Farris, Russell & Thomsen Reference Farris, Russell and Thomsen1993), so that time dependency and wave activity are weak (see, however, Wilson III et al. (Reference Wilson, Koval, Szabo, Stevens, Kasper, Cattell and Krasnoselskikh2017)). Therefore, one can expect that in low Mach number shocks macroscopic fields dominate. With the increase of the Mach number shocks become more time dependent and wave activity increases. By time dependence we mean here non-stationarity of the shock structure at spatial scales of the ramp and larger and temporal scales of the order of the ion gyroperiod, while wave activity may refer to any feature of a smaller spatial and/or temporal scale. High Mach number shocks are expected to be reforming (Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Formisano and Neugebauer1975; Scudder et al.
Reference Scudder, Aggson, Mangeney, Lacombe and Harvey1986; Newbury, Russell & Gedalin Reference Newbury, Russell and Gedalin1998; Krasnoselskikh et al.
Reference Krasnoselskikh, Lembège, Savoini and Lobzin2002; Scholer & Matsukiyo Reference Scholer and Matsukiyo2004; Burgess & Scholer Reference Burgess and Scholer2007; Lobzin et al.
Reference Lobzin, Krasnoselskikh, Bosqued, Pinçon, Schwartz and Dunlop2007; Scholer & Burgess Reference Scholer and Burgess2007; Lobzin et al.
Reference Lobzin, Krasnoselskikh, Musatenko and de Wit2008; Lembège et al.
Reference Lembège, Savoini, Hellinger and Trávníček2009; Yang et al.
Reference Yang, Lu, Lembège and Wang2009; Mazelle et al.
Reference Mazelle, Lembège, Morgenthaler, Meziane, Horbury, Génot, Lucek, Dandouras, Maksimovic and Issautier2010; Umeda et al.
Reference Umeda, Kidani, Yamao, Matsukiyo and Yamazaki2010; Comişel et al.
Reference Comişel, Scholer, Soucek and Matsukiyo2011; Kajdič et al.
Reference Kajdič, Blanco-Cano, Aguilar-Rodriguez, Russell, Jian and Luhmann2012; Wilson et al.
Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2012; Dimmock et al.
Reference Dimmock, Russell, Sagdeev, Krasnoselskikh, Walker, Carr, Dandouras, Escoubet, Ganushkina and Gedalin2019). In such shocks the macroscopic fields become essentially time dependent, in addition to strong microscopic fields. When a shock Mach number exceeds the critical value, resistivity and thermal conduction can no longer sustain the shock profile (Coroniti Reference Coroniti1970; Edmiston & Kennel Reference Edmiston and Kennel1984; Kennel Reference Kennel1987). Supercritical shocks have structured profiles (Newbury, Russell & Gedalin Reference Newbury, Russell and Gedalin1998) and ion reflection is expected to play an important role. For moderately supercritical shocks time dependence of macroscopic fields is still weak while the amplitude of microscopic fields rapidly increases with the increase of the Mach number. One therefore could expect that in higher Mach number shocks the role of microscopic fields becomes progressively more important. Until now relative influence of the macroscopic and microscopic fields on ion motion has not been analysed quantitatively. Figure 1 illustrates what we mean by macroscopic and microscopic fields. The figure presents magnetic profiles,
$\unicode[STIX]{x1D6FD}$
shocks are nearly one-dimensional and stationary (Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Formisano and Neugebauer1975; Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Gosling, Bame, Paschmann, Parks, Anderson, Anderson and Gurnett1980; Russell et al.
Reference Russell, Hoppe, Livesey and Gosling1982; Mellott & Greenstadt Reference Mellott and Greenstadt1984; Farris, Russell & Thomsen Reference Farris, Russell and Thomsen1993), so that time dependency and wave activity are weak (see, however, Wilson III et al. (Reference Wilson, Koval, Szabo, Stevens, Kasper, Cattell and Krasnoselskikh2017)). Therefore, one can expect that in low Mach number shocks macroscopic fields dominate. With the increase of the Mach number shocks become more time dependent and wave activity increases. By time dependence we mean here non-stationarity of the shock structure at spatial scales of the ramp and larger and temporal scales of the order of the ion gyroperiod, while wave activity may refer to any feature of a smaller spatial and/or temporal scale. High Mach number shocks are expected to be reforming (Greenstadt et al.
Reference Greenstadt, Scarf, Russell, Formisano and Neugebauer1975; Scudder et al.
Reference Scudder, Aggson, Mangeney, Lacombe and Harvey1986; Newbury, Russell & Gedalin Reference Newbury, Russell and Gedalin1998; Krasnoselskikh et al.
Reference Krasnoselskikh, Lembège, Savoini and Lobzin2002; Scholer & Matsukiyo Reference Scholer and Matsukiyo2004; Burgess & Scholer Reference Burgess and Scholer2007; Lobzin et al.
Reference Lobzin, Krasnoselskikh, Bosqued, Pinçon, Schwartz and Dunlop2007; Scholer & Burgess Reference Scholer and Burgess2007; Lobzin et al.
Reference Lobzin, Krasnoselskikh, Musatenko and de Wit2008; Lembège et al.
Reference Lembège, Savoini, Hellinger and Trávníček2009; Yang et al.
Reference Yang, Lu, Lembège and Wang2009; Mazelle et al.
Reference Mazelle, Lembège, Morgenthaler, Meziane, Horbury, Génot, Lucek, Dandouras, Maksimovic and Issautier2010; Umeda et al.
Reference Umeda, Kidani, Yamao, Matsukiyo and Yamazaki2010; Comişel et al.
Reference Comişel, Scholer, Soucek and Matsukiyo2011; Kajdič et al.
Reference Kajdič, Blanco-Cano, Aguilar-Rodriguez, Russell, Jian and Luhmann2012; Wilson et al.
Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2012; Dimmock et al.
Reference Dimmock, Russell, Sagdeev, Krasnoselskikh, Walker, Carr, Dandouras, Escoubet, Ganushkina and Gedalin2019). In such shocks the macroscopic fields become essentially time dependent, in addition to strong microscopic fields. When a shock Mach number exceeds the critical value, resistivity and thermal conduction can no longer sustain the shock profile (Coroniti Reference Coroniti1970; Edmiston & Kennel Reference Edmiston and Kennel1984; Kennel Reference Kennel1987). Supercritical shocks have structured profiles (Newbury, Russell & Gedalin Reference Newbury, Russell and Gedalin1998) and ion reflection is expected to play an important role. For moderately supercritical shocks time dependence of macroscopic fields is still weak while the amplitude of microscopic fields rapidly increases with the increase of the Mach number. One therefore could expect that in higher Mach number shocks the role of microscopic fields becomes progressively more important. Until now relative influence of the macroscopic and microscopic fields on ion motion has not been analysed quantitatively. Figure 1 illustrates what we mean by macroscopic and microscopic fields. The figure presents magnetic profiles,
![]() $|B|$
, measured at two bow shock crossings by CLUSTER. The measured profiles are shown in black. The red curves are the profiles with the microscopic fields removed. The removal was done by applying discrete wavelet transform, removing a number of finest levels and further applying inverse transform (Kumar & Foufoula-Georgiou Reference Kumar and Foufoula-Georgiou1997; Gedalin, Newbury & Russell Reference Gedalin, Newbury and Russell1998; Torrence & Compo Reference Torrence and Compo1998; Gedalin, Newbury & Russell Reference Gedalin, Newbury and Russell2000). Daubechies 10 wavelet was used in both cases. The magnetic field in (a) is measured with the sampling rate of 22 Hz. The
$|B|$
, measured at two bow shock crossings by CLUSTER. The measured profiles are shown in black. The red curves are the profiles with the microscopic fields removed. The removal was done by applying discrete wavelet transform, removing a number of finest levels and further applying inverse transform (Kumar & Foufoula-Georgiou Reference Kumar and Foufoula-Georgiou1997; Gedalin, Newbury & Russell Reference Gedalin, Newbury and Russell1998; Torrence & Compo Reference Torrence and Compo1998; Gedalin, Newbury & Russell Reference Gedalin, Newbury and Russell2000). Daubechies 10 wavelet was used in both cases. The magnetic field in (a) is measured with the sampling rate of 22 Hz. The
![]() $2^{12}$
point data were processed and the 8 lowest levels were retained. Panel (b) has sampling rate of 67 Hz,
$2^{12}$
point data were processed and the 8 lowest levels were retained. Panel (b) has sampling rate of 67 Hz,
![]() $2^{14}$
points, and 6 levels retained. The higher is the sampling rate the more fluctuations are measured and stronger denoising is required to remove these fluctuations. The difference between the black and red curves is what is called here the microscopic fields. Denoising is not unambiguous and, in principle, should be verified a posteriori in an indirect way, by analysing consequences of the cleaning for the processes in the shock and comparing with observations. Here figure 1 is for illustrative purposes only. As a side note: the small-scale fluctuations in (b) resemble the waves generated by the ramp and propagating to both directions, as argued by Granit & Gedalin (Reference Granit and Gedalin2018). This is only a speculation at this stage though.
$2^{14}$
points, and 6 levels retained. The higher is the sampling rate the more fluctuations are measured and stronger denoising is required to remove these fluctuations. The difference between the black and red curves is what is called here the microscopic fields. Denoising is not unambiguous and, in principle, should be verified a posteriori in an indirect way, by analysing consequences of the cleaning for the processes in the shock and comparing with observations. Here figure 1 is for illustrative purposes only. As a side note: the small-scale fluctuations in (b) resemble the waves generated by the ramp and propagating to both directions, as argued by Granit & Gedalin (Reference Granit and Gedalin2018). This is only a speculation at this stage though.

Figure 1. Two shocks observed by CLUSTER.
To summarize, we distinguish between the possibly time-dependent macroscopic field (the red curves in figure 1) and the presumably fast time/space-varying microscopic fields. The first will be also referred to as a non-stationary shock structure while the latter will be referred to as fluctuations. The objective of the present paper is to establish whether macroscopic fields still dominate ion motion even when these fields become time dependent. If yes, to what extent does the relation of the ion motion to the magnetic field change?
2 The framework
In the absence of binary collisions, the motion of each charged particle within the shock front is governed by the total self-consistent electric and magnetic fields which are, in general, space and time dependent. Knowing these fields one could, in principle, find the distribution functions of all charged particles. The latter would provide the charge and current densities and the fields themselves via Maxwell’s equations. It is not possible at present to have a self-consistent solution of the kinetic (Vlasov) and Maxwell equations. It is possible to simplify the problem using reasonable assumptions and to seek solutions which are partially self-consistent. Since the best available in situ measurements at shocks are magnetic field measurements in the heliosphere, we focus on the relation of the particle motion to the magnetic field. The magnetic field can be regarded as shaped by particles via the momentum conservation laws
Here
![]() $s$
denotes species (electrons, protons, alpha particles);
$s$
denotes species (electrons, protons, alpha particles);
![]() $i,j=x,y,z$
and
$i,j=x,y,z$
and
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker tensor. The density, hydrodynamical velocity and total pressure tensor are defined using the distribution function,
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker tensor. The density, hydrodynamical velocity and total pressure tensor are defined using the distribution function,
The total pressure includes both dynamic pressure
![]() $P_{\text{dyn},ij}=nmV_{i}V_{j}$
and kinetic pressure. The conservation law (2.1) is exact and should be valid for stationary and time-dependent fields as well. In a one-dimensional stationary shock it reduces to
$P_{\text{dyn},ij}=nmV_{i}V_{j}$
and kinetic pressure. The conservation law (2.1) is exact and should be valid for stationary and time-dependent fields as well. In a one-dimensional stationary shock it reduces to
throughout the shock. Here the shock normal is chosen to be along the
![]() $x$
-axis. In particular, the magnetic field magnitude should satisfy the pressure balance equation
$x$
-axis. In particular, the magnetic field magnitude should satisfy the pressure balance equation
Here, subscript
![]() $u$
denotes upstream and we assumed upstream thermal distributions for all species. The equation is written in the normal incidence frame (NIF) where the upstream plasma velocity is along the shock normal and equal to
$u$
denotes upstream and we assumed upstream thermal distributions for all species. The equation is written in the normal incidence frame (NIF) where the upstream plasma velocity is along the shock normal and equal to
![]() $V_{u}$
. Accordingly, the upstream velocities of all species are also
$V_{u}$
. Accordingly, the upstream velocities of all species are also
![]() $V_{u}$
along the shock normal.
$V_{u}$
along the shock normal.
Following the described separation of the fields we shall treat the magnetic field variations at spatial scales substantially less than the proton inertial length,
![]() ${\lesssim}(c/\unicode[STIX]{x1D714}_{pp})$
, and/or at a temporal scale substantially less than the inverse proton gyrofrequency,
${\lesssim}(c/\unicode[STIX]{x1D714}_{pp})$
, and/or at a temporal scale substantially less than the inverse proton gyrofrequency,
![]() ${\lesssim}(1/\unicode[STIX]{x1D6FA}_{p})$
, as fast-varying fields. The only exception is the magnetic ramp whose width may be less than
${\lesssim}(1/\unicode[STIX]{x1D6FA}_{p})$
, as fast-varying fields. The only exception is the magnetic ramp whose width may be less than
![]() $(c/\unicode[STIX]{x1D714}_{pp})$
since it is the main magnetic jump in the shock. Here
$(c/\unicode[STIX]{x1D714}_{pp})$
since it is the main magnetic jump in the shock. Here
![]() $\unicode[STIX]{x1D714}_{pp}^{2}=4\unicode[STIX]{x03C0}n_{u}e^{2}/m_{p}$
and
$\unicode[STIX]{x1D714}_{pp}^{2}=4\unicode[STIX]{x03C0}n_{u}e^{2}/m_{p}$
and
![]() $\unicode[STIX]{x1D6FA}_{p}=eB_{u}/m_{p}c$
, where the subscript
$\unicode[STIX]{x1D6FA}_{p}=eB_{u}/m_{p}c$
, where the subscript
![]() $u$
refers to the asymptotically uniform upstream region. The fast-varying fields affect electron motion strongly (Wilson et al.
Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2012, Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina2014a
,Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina
b
). However, for any ion species they play the role of weak scattering only. Indeed, the relative momentum change during an ion passing through such a small-scale fluctuation is
$u$
refers to the asymptotically uniform upstream region. The fast-varying fields affect electron motion strongly (Wilson et al.
Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2012, Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina2014a
,Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina
b
). However, for any ion species they play the role of weak scattering only. Indeed, the relative momentum change during an ion passing through such a small-scale fluctuation is
![]() $\unicode[STIX]{x0394}p/p\sim (FL/v)/p$
, where
$\unicode[STIX]{x0394}p/p\sim (FL/v)/p$
, where
![]() $F$
is the force acting on the ion within the fluctuation,
$F$
is the force acting on the ion within the fluctuation,
![]() $L$
is the typical scale of it and
$L$
is the typical scale of it and
![]() $v$
is the typical ion speed. It is easy to see that the relative change due to the electric field is of the order of
$v$
is the typical ion speed. It is easy to see that the relative change due to the electric field is of the order of
![]() $e\unicode[STIX]{x1D711}/mV^{2}$
, where
$e\unicode[STIX]{x1D711}/mV^{2}$
, where
![]() $\unicode[STIX]{x1D711}\sim EL$
is the ‘cross-fluctuation’ potential. As long as this potential is a tiny fraction of the ion kinetic energy, the ion experiences only a small kick upon interaction with this field. Similarly, for the magnetic effect we will have a relative change of at most
$\unicode[STIX]{x1D711}\sim EL$
is the ‘cross-fluctuation’ potential. As long as this potential is a tiny fraction of the ion kinetic energy, the ion experiences only a small kick upon interaction with this field. Similarly, for the magnetic effect we will have a relative change of at most
![]() $\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FA}_{p}$
where
$\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FA}_{p}$
where
![]() $\unicode[STIX]{x1D70F}$
is the crossing time of the small-scale feature. Since
$\unicode[STIX]{x1D70F}$
is the crossing time of the small-scale feature. Since
![]() $\unicode[STIX]{x1D70F}\ll 1/\unicode[STIX]{x1D6FA}_{p}$
, the relative change is small. If the fluctuations are bipolar (Wilson et al.
Reference Wilson, Cattell, Kellogg, Goetz, Kersten, Kasper, Szabo and Wilber2010, Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina2014c
), the relative change on a large number of fluctuations will be quadratic on the smallness parameter. Thus, the fast-varying fluctuations play the role of effective scattering for ions and the mean free path of this scattering exceeds by far the region of the size of several ion convective gyroradii,
$\unicode[STIX]{x1D70F}\ll 1/\unicode[STIX]{x1D6FA}_{p}$
, the relative change is small. If the fluctuations are bipolar (Wilson et al.
Reference Wilson, Cattell, Kellogg, Goetz, Kersten, Kasper, Szabo and Wilber2010, Reference Wilson, Sibeck, Breneman, Contel, Cully, Turner, Angelopoulos and Malaspina2014c
), the relative change on a large number of fluctuations will be quadratic on the smallness parameter. Thus, the fast-varying fluctuations play the role of effective scattering for ions and the mean free path of this scattering exceeds by far the region of the size of several ion convective gyroradii,
![]() $r_{g}=V_{u}/\unicode[STIX]{x1D6FA}_{p}$
, around the ramp. It is this region we are focused on.
$r_{g}=V_{u}/\unicode[STIX]{x1D6FA}_{p}$
, around the ramp. It is this region we are focused on.
The conservation laws (2.1) include both slow and fast variations. In what follows we restrict ourselves to the
![]() $xx$
-component only as the most important since the momentum is carried along the shock normal and for simplicity we assume dependence on
$xx$
-component only as the most important since the momentum is carried along the shock normal and for simplicity we assume dependence on
![]() $t$
and
$t$
and
![]() $x$
only. Averaging over fast variations one gets
$x$
only. Averaging over fast variations one gets
where on the left-hand side now only slowly varying quantities are retained. The contribution of the fast-varying fields is taken into account by excluding electrons from the kinetic description and using a hydrodynamical equation of state for them. Equation (2.7) describes non-stationarity of macroscopic fields together with ion distributions produced by these macroscopic fields, while the electron pressure
![]() $P_{e}$
absorbs the contribution of the fast-varying fields. Summation is now over ion species only. The strength of deviations from stationarity can be now estimated by verification of the validity of (2.5). This is the objective of the forthcoming sections.
$P_{e}$
absorbs the contribution of the fast-varying fields. Summation is now over ion species only. The strength of deviations from stationarity can be now estimated by verification of the validity of (2.5). This is the objective of the forthcoming sections.
3 Hybrid simulation
We start with a hybrid simulation of a supercritical shock. The simulation is done using the dHybrid code (Gargaté et al.
Reference Gargaté, Bingham, Fonseca and Silva2007; Caprioli & Spitkovsky Reference Caprioli and Spitkovsky2014). The simulation is in the plane
![]() $x{-}z$
, with a box size
$x{-}z$
, with a box size
![]() $L_{x}\times L_{z}=80(c/\unicode[STIX]{x1D714}_{pp})\times 1(c/\unicode[STIX]{x1D714}_{pp})$
and grid spacing of
$L_{x}\times L_{z}=80(c/\unicode[STIX]{x1D714}_{pp})\times 1(c/\unicode[STIX]{x1D714}_{pp})$
and grid spacing of
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}z=0.1(c/\unicode[STIX]{x1D714}_{pp})$
. Periodic boundary conditions are imposed across the box. Along the box one side is a reflecting wall and the other side is open, with a constant injection of particles. The small perpendicular size of the box allows us to focus on the time dependence of the shock. Larger widths would be required to include also the effects of rippling, which latter is expected to develop at higher Mach number (Ofman & Gedalin Reference Ofman and Gedalin2013a
). For the parameters chosen in this study, rippling is negligible (Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019) and use of a narrow simulation box is justified. The upstream magnetic field is in the simulation plane and the angle is
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}z=0.1(c/\unicode[STIX]{x1D714}_{pp})$
. Periodic boundary conditions are imposed across the box. Along the box one side is a reflecting wall and the other side is open, with a constant injection of particles. The small perpendicular size of the box allows us to focus on the time dependence of the shock. Larger widths would be required to include also the effects of rippling, which latter is expected to develop at higher Mach number (Ofman & Gedalin Reference Ofman and Gedalin2013a
). For the parameters chosen in this study, rippling is negligible (Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019) and use of a narrow simulation box is justified. The upstream magnetic field is in the simulation plane and the angle is
![]() $\unicode[STIX]{x1D703}_{Bn}=70^{\circ }$
. Two ion species, protons and alpha particles, are treated within the particle-in-cell approach, while electrons are treated as a massless neutralizing fluid with a polytropic state equation
$\unicode[STIX]{x1D703}_{Bn}=70^{\circ }$
. Two ion species, protons and alpha particles, are treated within the particle-in-cell approach, while electrons are treated as a massless neutralizing fluid with a polytropic state equation
![]() $P_{e}/n_{e}^{\unicode[STIX]{x1D6FE}}=\text{const.}$
,
$P_{e}/n_{e}^{\unicode[STIX]{x1D6FE}}=\text{const.}$
,
![]() $\unicode[STIX]{x1D6FE}=5/3$
. There are 64 particles per cell (p.p.c.) for each species and
$\unicode[STIX]{x1D6FE}=5/3$
. There are 64 particles per cell (p.p.c.) for each species and
![]() $n_{\unicode[STIX]{x1D6FC}u}/n_{pu}=0.05$
. Increase or decrease of the p.p.c. by a factor of two has not shown any noticeable changes except rapid increase of lapse time for larger p.p.c. numbers. The time step is
$n_{\unicode[STIX]{x1D6FC}u}/n_{pu}=0.05$
. Increase or decrease of the p.p.c. by a factor of two has not shown any noticeable changes except rapid increase of lapse time for larger p.p.c. numbers. The time step is
![]() $0.0025(1/\unicode[STIX]{x1D6FA}_{p})$
and the system is run for
$0.0025(1/\unicode[STIX]{x1D6FA}_{p})$
and the system is run for
![]() $60/\unicode[STIX]{x1D6FA}_{p}$
. The proton Alfvén speed is defined as
$60/\unicode[STIX]{x1D6FA}_{p}$
. The proton Alfvén speed is defined as
![]() $v_{pA}^{2}=B_{u}^{2}/4\unicode[STIX]{x03C0}n_{pu}m_{p}$
, where
$v_{pA}^{2}=B_{u}^{2}/4\unicode[STIX]{x03C0}n_{pu}m_{p}$
, where
![]() $m_{p}$
is the proton mass. All speeds are defined in terms of the proton Alfvén speed, so that the Mach number is
$m_{p}$
is the proton mass. All speeds are defined in terms of the proton Alfvén speed, so that the Mach number is
![]() $V_{u}/v_{pA}$
, where
$V_{u}/v_{pA}$
, where
![]() $V_{u}$
is the plasma flow speed in the normal incidence frame (shock frame). Accordingly, the injection speed
$V_{u}$
is the plasma flow speed in the normal incidence frame (shock frame). Accordingly, the injection speed
![]() $v_{\text{in}}=2.5$
. Temperature ratios in the solar wind vary in a wide range (Wilson et al.
Reference Wilson, Stevens, Kasper, Klein, Maruca, Bale, Bowen, Pulupa and Salem2018). In the present simulations we choose the thermal speeds of both species equal
$v_{\text{in}}=2.5$
. Temperature ratios in the solar wind vary in a wide range (Wilson et al.
Reference Wilson, Stevens, Kasper, Klein, Maruca, Bale, Bowen, Pulupa and Salem2018). In the present simulations we choose the thermal speeds of both species equal
![]() $v_{T\unicode[STIX]{x1D6FC}}=v_{Tp}=0.4$
. The electron temperature is
$v_{T\unicode[STIX]{x1D6FC}}=v_{Tp}=0.4$
. The electron temperature is
![]() $T_{e}=0.2(m_{p}v_{pA}^{2}/2)$
. Thermal parameters are often expressed in terms of
$T_{e}=0.2(m_{p}v_{pA}^{2}/2)$
. Thermal parameters are often expressed in terms of
![]() $\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{p}T/B_{u}^{2}$
,
$\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}n_{p}T/B_{u}^{2}$
,
![]() $\unicode[STIX]{x1D6FD}_{i}=2v_{Ti}^{2}$
,
$\unicode[STIX]{x1D6FD}_{i}=2v_{Ti}^{2}$
,
![]() $i=p,\unicode[STIX]{x1D6FC}$
and
$i=p,\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}_{e}=2T_{e}$
. The total upstream thermal pressure is
$\unicode[STIX]{x1D6FD}_{e}=2T_{e}$
. The total upstream thermal pressure is
![]() $n_{e}T_{e}+n_{p}T_{p}+n_{A}T_{A}$
, where
$n_{e}T_{e}+n_{p}T_{p}+n_{A}T_{A}$
, where
![]() $n_{e}=n_{p}+2n_{A}$
, which gives
$n_{e}=n_{p}+2n_{A}$
, which gives
![]() $\unicode[STIX]{x1D6FD}_{u}\approx 0.7$
. It is worth noting that the true MHD (magnetohydrodynamical) Alfvén speed is
$\unicode[STIX]{x1D6FD}_{u}\approx 0.7$
. It is worth noting that the true MHD (magnetohydrodynamical) Alfvén speed is
![]() $v_{A}^{2}=B_{u}^{2}/4\unicode[STIX]{x03C0}(n_{pu}m_{p}+n_{Au}m_{A})=v_{pA}^{2}(1+4n_{Au}/n_{pu})$
. Therefore, the MHD Mach number is
$v_{A}^{2}=B_{u}^{2}/4\unicode[STIX]{x03C0}(n_{pu}m_{p}+n_{Au}m_{A})=v_{pA}^{2}(1+4n_{Au}/n_{pu})$
. Therefore, the MHD Mach number is
![]() $M_{A}=M\sqrt{1.2}\approx 1.1M$
.
$M_{A}=M\sqrt{1.2}\approx 1.1M$
.

Figure 2. Magnetic field: hybrid simulation.
dHybrid applies 3-point averaging which effectively damps all small-scale and high-frequency fluctuations, so that only macroscopic fields remain in the simulation. The macroscopic magnetic fields is time dependent, as is seen from figure 2, where several magnetic profiles averaged across the
![]() $z$
-direction of the simulation box are shown. The temporal separation between subsequent profiles is
$z$
-direction of the simulation box are shown. The temporal separation between subsequent profiles is
![]() $\unicode[STIX]{x0394}t=2.5/\unicode[STIX]{x1D6FA}_{p}$
. They are shifted by
$\unicode[STIX]{x0394}t=2.5/\unicode[STIX]{x1D6FA}_{p}$
. They are shifted by
![]() $v_{\text{sh}}\unicode[STIX]{x0394}t$
where the average shock speed is found to be
$v_{\text{sh}}\unicode[STIX]{x0394}t$
where the average shock speed is found to be
![]() $v_{\text{sh}}=1.16$
, which gives the Mach number of the shock of
$v_{\text{sh}}=1.16$
, which gives the Mach number of the shock of
![]() $M=3.66$
(compare to Ofman et al. (Reference Ofman, Koval, Wilson and Szabo2019), who forgot to add the shock speed to the injection speed). The profiles do not coincide completely which means that the shock speed measured by the ramp position is not constant. In other words, the ramp position is time dependent in the shock frame and weakly oscillates. Such weak time dependence of moderately supercritical shocks has been found recently in other hybrid simulations (Gedalin Reference Gedalin2019a
; Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019). It is worth noting that hybrid simulations show that shock formation and stable existence do not require the presence of microscopic fields (Burgess, Wilkinson & Schwartz Reference Burgess, Wilkinson and Schwartz1989; Sckopke et al.
Reference Sckopke, Paschmann, Brinca, Carlson and Luehr1990; Scholer & Matsukiyo Reference Scholer and Matsukiyo2004; Moullard et al.
Reference Moullard, Burgess, Horbury and Lucek2006; Burgess & Scholer Reference Burgess and Scholer2007; Scholer & Burgess Reference Scholer and Burgess2007; Comişel et al.
Reference Comişel, Scholer, Soucek and Matsukiyo2011; Ofman & Gedalin Reference Ofman and Gedalin2013a
,Reference Ofman and Gedalin
b
; Gedalin Reference Gedalin2019a
; Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019). The macroscopic fields dominate ion motion and ion distribution formation. These distributions, in turn, shape the shock profile.
$M=3.66$
(compare to Ofman et al. (Reference Ofman, Koval, Wilson and Szabo2019), who forgot to add the shock speed to the injection speed). The profiles do not coincide completely which means that the shock speed measured by the ramp position is not constant. In other words, the ramp position is time dependent in the shock frame and weakly oscillates. Such weak time dependence of moderately supercritical shocks has been found recently in other hybrid simulations (Gedalin Reference Gedalin2019a
; Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019). It is worth noting that hybrid simulations show that shock formation and stable existence do not require the presence of microscopic fields (Burgess, Wilkinson & Schwartz Reference Burgess, Wilkinson and Schwartz1989; Sckopke et al.
Reference Sckopke, Paschmann, Brinca, Carlson and Luehr1990; Scholer & Matsukiyo Reference Scholer and Matsukiyo2004; Moullard et al.
Reference Moullard, Burgess, Horbury and Lucek2006; Burgess & Scholer Reference Burgess and Scholer2007; Scholer & Burgess Reference Scholer and Burgess2007; Comişel et al.
Reference Comişel, Scholer, Soucek and Matsukiyo2011; Ofman & Gedalin Reference Ofman and Gedalin2013a
,Reference Ofman and Gedalin
b
; Gedalin Reference Gedalin2019a
; Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019). The macroscopic fields dominate ion motion and ion distribution formation. These distributions, in turn, shape the shock profile.

Figure 3. Proton (blue) and alpha-particle (red) density evolution throughout the shock (hybrid simulation).

Figure 4. Orbits
![]() $x{-}v_{x}$
of protons (black) and alpha particles (blue) throughout the shock (hybrid simulation). The magnetic field profile is shown in red.
$x{-}v_{x}$
of protons (black) and alpha particles (blue) throughout the shock (hybrid simulation). The magnetic field profile is shown in red.
Figure 3 shows the proton and alpha particle densities in the shock front as obtained in the hybrid simulation. The densities of the species are normalized to their upstream densities. The density oscillations were misinterpreted as surfing (Ofman et al.
Reference Ofman, Koval, Wilson and Szabo2019) while in fact they are only a manifestation of ion gyration, as seen in figure 4. The orbits and the density oscillations are very similar to what occurs in low Mach number shocks and have been comprehensively explained by the theory of kinematic collisionless relaxation (Balikhin et al.
Reference Balikhin, Zhang, Gedalin, Ganushkina and Pope2008; Ofman et al.
Reference Ofman, Balikhin, Russell and Gedalin2009; Ofman & Gedalin Reference Ofman and Gedalin2013b
; Gedalin Reference Gedalin2015; Gedalin, Friedman & Balikhin Reference Gedalin, Friedman and Balikhin2015; Gedalin Reference Gedalin2016, Reference Gedalin2017; Pope, Gedalin & Balikhin Reference Pope, Gedalin and Balikhin2019). Surfing or multiple reflection (Lee, Shapiro & Sagdeev Reference Lee, Shapiro and Sagdeev1996; Zank et al.
Reference Zank, Pauls, Cairns and Webb1996) require that ions stay for a large number of gyroperiods in the vicinity of the ramp, while here all ions proceed further downstream immediately. Reflected ions are clearly seen in figure 4 which supports the conclusion that the shock is supercritical. In addition, figure 5 shows the gyrophase bunched distributions of reflected ions inside the ramp. The MHD Alfvén Mach number for this shock is
![]() $M_{A}=4$
. The fast magnetosonic Mach number is
$M_{A}=4$
. The fast magnetosonic Mach number is
![]() $M_{F}\approx 3.2$
while the critical fast Mach number is
$M_{F}\approx 3.2$
while the critical fast Mach number is
![]() $M_{c}=2.54$
.
$M_{c}=2.54$
.

Figure 5. Proton (a) and alpha particle (b) distributions in the plane
![]() $v_{x}{-}v_{y}$
within the ramp (hybrid simulation).
$v_{x}{-}v_{y}$
within the ramp (hybrid simulation).
4 Ion tracing in the numerically obtained fields
The simulated shock is non-stationary. In order to quantify this effect, we perform ion tracing in the fields found in the simulation at
![]() $t=50/\unicode[STIX]{x1D6FA}_{u}$
as if these fields were time independent. The shock angle, the Mach number and the temperatures of the incident populations are identical to those in the hybrid simulation. The tracing provides distributions of protons and alpha particles throughout the shock which allows us to calculate
$t=50/\unicode[STIX]{x1D6FA}_{u}$
as if these fields were time independent. The shock angle, the Mach number and the temperatures of the incident populations are identical to those in the hybrid simulation. The tracing provides distributions of protons and alpha particles throughout the shock which allows us to calculate
![]() $P_{xx}$
and derive the magnetic field from the pressure balance (2.5). The derived magnetic field is further compared to the simulated magnetic field. The cross-shock electric field used in the analysis is shown in figure 6. Figure 7 presents a comparison of the magnetic field magnitude found in the hybrid simulation (blue curve) with the magnetic field magnitude calculated from the pressure balance (2.5) (red curve) with the ion distributions found with tracing in static fields. The two magnetic profiles agree much better than could be expected given that the shock was found to be non-stationary in the hybrid simulation. The differences are minor, which means that pressure balance is nearly maintained throughout the shock front.
$P_{xx}$
and derive the magnetic field from the pressure balance (2.5). The derived magnetic field is further compared to the simulated magnetic field. The cross-shock electric field used in the analysis is shown in figure 6. Figure 7 presents a comparison of the magnetic field magnitude found in the hybrid simulation (blue curve) with the magnetic field magnitude calculated from the pressure balance (2.5) (red curve) with the ion distributions found with tracing in static fields. The two magnetic profiles agree much better than could be expected given that the shock was found to be non-stationary in the hybrid simulation. The differences are minor, which means that pressure balance is nearly maintained throughout the shock front.

Figure 6. Cross-shock electric field found in the hybrid simulation and used in the test particle analysis.

Figure 7. Magnetic field from hybrid simulation (blue) versus magnetic field from pressure balance with ion tracing in the simulated fields (red).
Figure 8 shows the orbits
![]() $x{-}v_{x}$
of approximately 80 particles of each species. The orbits are derived as if the numerically found fields were static. This figure should be compared with figure 4. In both cases the orbits clearly show identical maxima and minima and correlation of local maxima of velocity and minima of the magnetic fields, as required by the pressure balance (Gedalin Reference Gedalin2015; Gedalin et al.
Reference Gedalin, Friedman and Balikhin2015).
$x{-}v_{x}$
of approximately 80 particles of each species. The orbits are derived as if the numerically found fields were static. This figure should be compared with figure 4. In both cases the orbits clearly show identical maxima and minima and correlation of local maxima of velocity and minima of the magnetic fields, as required by the pressure balance (Gedalin Reference Gedalin2015; Gedalin et al.
Reference Gedalin, Friedman and Balikhin2015).

Figure 8. Orbits
![]() $x{-}v_{x}$
of protons (black) and alpha particles (blue) throughout the shock, as derived from ion tracing in the numerically found fields if assumed static. The magnetic field profile is shown in red.
$x{-}v_{x}$
of protons (black) and alpha particles (blue) throughout the shock, as derived from ion tracing in the numerically found fields if assumed static. The magnetic field profile is shown in red.
Distributions of protons (a) and alpha particles (b) inside the ramp, as obtained with ion tracing in the numerically found fields, are shown in figure 9. The distributions are produced in different ways in the hybrid simulations and in the ion tracing. In the hybrid simulations a snapshot at some moment provides velocities of all particles inside the box and the distribution is built afterwards. In the ion tracing an ion contributes each time it crosses the region of interest (the staying time method). The time step is very small. As a result, the effective number of particles is too large to output the velocities, so that the distribution is constructed during the tracing. The similarity of the distributions obtained in the ion tracing (figure 9) and those obtained in the hybrid simulation (figure 5) is better than could be expected taking into account the shock non-stationarity. The last two figures indicate that weak time dependence of the macroscopic fields produces only minor effects on particle distributions.

Figure 9. Distributions within the ramp obtained by ion tracing in the numerically found fields with the assumption that they are stationary. (a) Protons. (b) Alpha particles.
5 Model fields
The ion tracing above has been performed in the numerically found fields assuming that they are not time dependent. Although these fields are non-stationary, as became clear from the hybrid simulation, some agreement could be expected when comparing the numerically found magnetic field with the field which would be consistent with ion dynamics in the stationary fields. The found agreement appeared to be much better than expected. We proceed further by replacing the numerically found fields with model stationary fields. We trace ions in these fields and derive the magnetic field from the pressure balance. The derived field is compared to the field found in the hybrid simulations. In doing so we would be interested in the most simple model which would include a minimum of the details revealed in the hybrid simulation. In earlier works on laminar shocks (Gedalin et al.
Reference Gedalin, Friedman and Balikhin2015; Gedalin Reference Gedalin2016, Reference Gedalin2017) a monotonic
![]() $\tanh$
-like magnetic profile was chosen. This was justified since overshoots were weak and their effect on ions at the shock crossing was minor. In supercritical shocks overshoots are substantial. The cross-shock potential essentially follows the magnetic profile (Gedalin & Balikhin Reference Gedalin and Balikhin2004; Dimmock et al.
Reference Dimmock, Balikhin, Krasnoselskikh, Walker, Bale and Hobara2012; Gedalin Reference Gedalin2017). Ion transmission and reflection are particularly sensitive to the potential drop at the ramp (Gedalin Reference Gedalin1996, Reference Gedalin2016). In the presence of an overshoot the cross-ramp potential may significantly differ from the total cross-shock potential, the latter being measured between the asymptotic uniform upstream and downstream states. We therefore include the overshoot in the model magnetic field discarding the rest of the downstream magnetic oscillations. The model is described using the following analytical expression,
$\tanh$
-like magnetic profile was chosen. This was justified since overshoots were weak and their effect on ions at the shock crossing was minor. In supercritical shocks overshoots are substantial. The cross-shock potential essentially follows the magnetic profile (Gedalin & Balikhin Reference Gedalin and Balikhin2004; Dimmock et al.
Reference Dimmock, Balikhin, Krasnoselskikh, Walker, Bale and Hobara2012; Gedalin Reference Gedalin2017). Ion transmission and reflection are particularly sensitive to the potential drop at the ramp (Gedalin Reference Gedalin1996, Reference Gedalin2016). In the presence of an overshoot the cross-ramp potential may significantly differ from the total cross-shock potential, the latter being measured between the asymptotic uniform upstream and downstream states. We therefore include the overshoot in the model magnetic field discarding the rest of the downstream magnetic oscillations. The model is described using the following analytical expression,

Figure 10. Magnetic field: applied analytical model (blue) versus predicted by pressure balance (red).
This expression gives a monotonic transition with a smoothly superimposed asymmetric overshoot. The parameters
![]() $R$
,
$R$
,
![]() $D$
,
$D$
,
![]() $B_{a}$
,
$B_{a}$
,
![]() $x_{l}$
,
$x_{l}$
,
![]() $W_{l}$
,
$W_{l}$
,
![]() $x_{r}$
and
$x_{r}$
and
![]() $W_{r}$
allow complete control over the magnetic compression, ramp width, overshoot position and strength and even the rising and descending slopes of the overshoot. The cross-shock electric field is chosen as
$W_{r}$
allow complete control over the magnetic compression, ramp width, overshoot position and strength and even the rising and descending slopes of the overshoot. The cross-shock electric field is chosen as
![]() $E_{x}\propto \text{d}B_{z}/\text{d}z$
with the coefficient of proportionality ensuring that the total normal incidence frame cross-shock potential equals the value found in the simulation. The model non-coplanar magnetic field is also chosen as
$E_{x}\propto \text{d}B_{z}/\text{d}z$
with the coefficient of proportionality ensuring that the total normal incidence frame cross-shock potential equals the value found in the simulation. The model non-coplanar magnetic field is also chosen as
![]() $B_{y}\propto \text{d}B_{z}/\text{d}x$
with the coefficient of proportionality ensuring that the total de Hoffmann–Teller frame cross-shock potential equals the value found in the simulation (Goodrich & Scudder Reference Goodrich and Scudder1984; Schwartz et al.
Reference Schwartz, Thomsen, Bame and Stansberry1988). The magnetic profile used in ion tracing is shown in figure 10 (blue curve), which also presents the magnetic field derived from the pressure balance (red). As can be expected, the derived magnetic field differs from the simulated one since only the overshoot is included in the model while the successive large amplitude downstream oscillations are not taken into account. Yet, even this oversimplified model correctly predicts the main features of the magnetic profile, namely, the downstream oscillations are anti-correlated with the pressure and there are two kinds of peaks corresponding to the contributions of protons and alpha particles. Comparison of the densities (figure 11 versus figure 3) shows that the densities, especially that of the alpha particles, are less sensitive to the downstream magnetic oscillations than the pressure. This is not surprising since the contribution of the higher energy tail of reflected and quasi-reflected ions is small for density but substantial for pressure. In both simulated and model produced density profiles, spatially damping large-amplitude oscillations are present, with the spatial period for the alpha particles twice as large as for the protons, exactly as expected from gyration and kinematic relaxation. This relaxation is also clearly seen in figure 12 which is to be compared with figure 4 and figure 8. All three show the same pattern of proton and alpha particle orbits. It should be taken into account that only a small part of the orbits is shown for ion tracings while all particles are presented for the hybrid simulation. Thus, figure 8 and figure 12 show sparser distributions than seen in figure 4, yet similar gyration and relaxation are clearly seen in all three.
$B_{y}\propto \text{d}B_{z}/\text{d}x$
with the coefficient of proportionality ensuring that the total de Hoffmann–Teller frame cross-shock potential equals the value found in the simulation (Goodrich & Scudder Reference Goodrich and Scudder1984; Schwartz et al.
Reference Schwartz, Thomsen, Bame and Stansberry1988). The magnetic profile used in ion tracing is shown in figure 10 (blue curve), which also presents the magnetic field derived from the pressure balance (red). As can be expected, the derived magnetic field differs from the simulated one since only the overshoot is included in the model while the successive large amplitude downstream oscillations are not taken into account. Yet, even this oversimplified model correctly predicts the main features of the magnetic profile, namely, the downstream oscillations are anti-correlated with the pressure and there are two kinds of peaks corresponding to the contributions of protons and alpha particles. Comparison of the densities (figure 11 versus figure 3) shows that the densities, especially that of the alpha particles, are less sensitive to the downstream magnetic oscillations than the pressure. This is not surprising since the contribution of the higher energy tail of reflected and quasi-reflected ions is small for density but substantial for pressure. In both simulated and model produced density profiles, spatially damping large-amplitude oscillations are present, with the spatial period for the alpha particles twice as large as for the protons, exactly as expected from gyration and kinematic relaxation. This relaxation is also clearly seen in figure 12 which is to be compared with figure 4 and figure 8. All three show the same pattern of proton and alpha particle orbits. It should be taken into account that only a small part of the orbits is shown for ion tracings while all particles are presented for the hybrid simulation. Thus, figure 8 and figure 12 show sparser distributions than seen in figure 4, yet similar gyration and relaxation are clearly seen in all three.
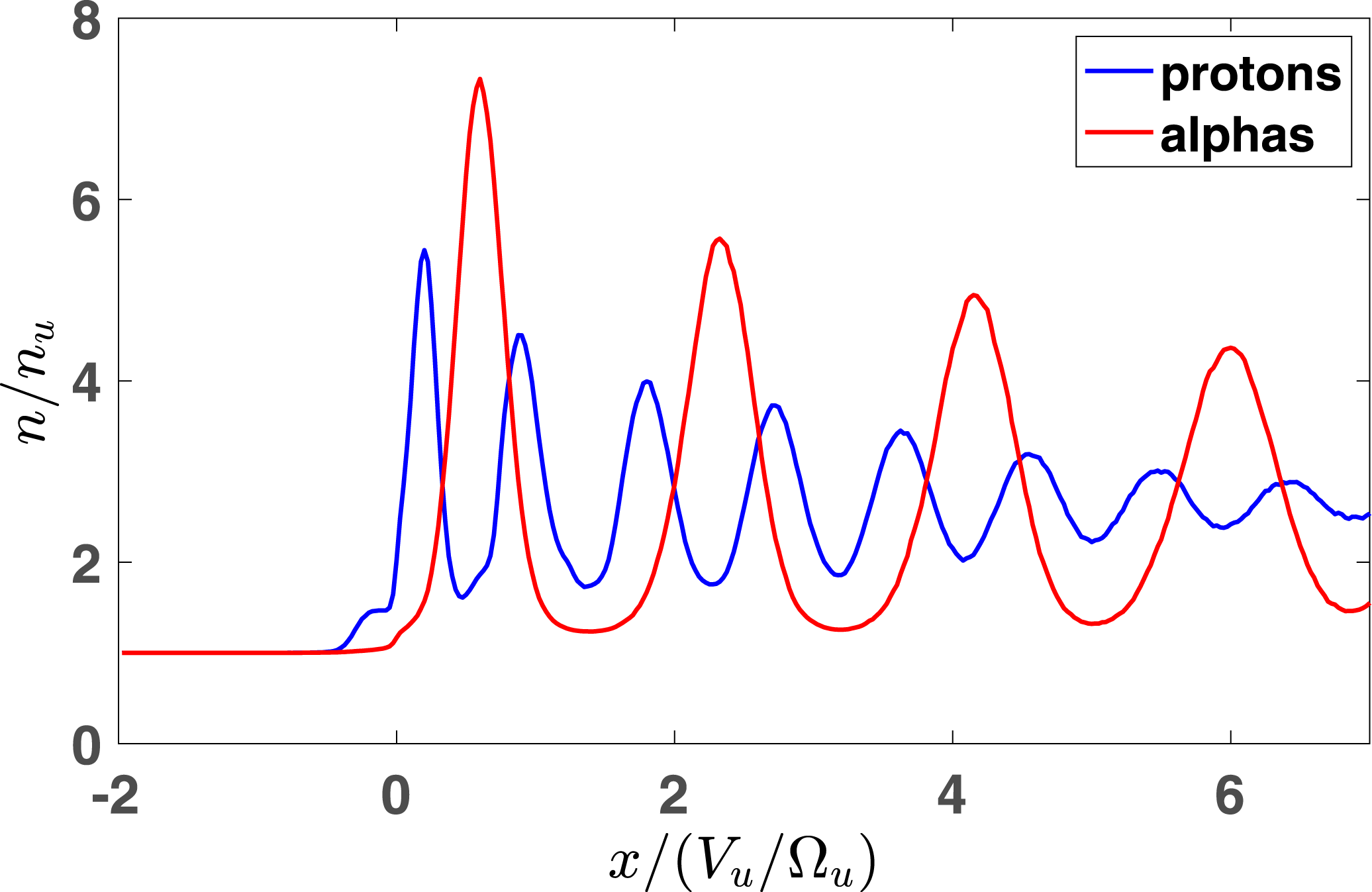
Figure 11. Proton (blue) and alpha particle (red) density obtained by ion tracing in the single overshoot model.

Figure 12. Orbits of protons (black) and alpha particles (blue) obtained by ion tracing in the single overshoot model.
6 Discussion and conclusions
In the present paper we applied a combined approach to study to what extent a supercritical shock is non-stationary. We started with a self-consistent hybrid simulation of a shock which showed that the shock is non-stationary. The simulations allowed us to evaluate deviations from stationarity by checking the instantaneous pressure balance. The pressure balance would have to be maintained exactly if the shock were planar and time independent. In order to quantify better the deviations, we applied ion tracing across a one-dimensional stationary shock when the magnetic and electric fields of the shock were taken from a single snapshot of the performed hybrid simulation as if they were time independent. The ion distributions throughout the shock were determined and again the pressure balance was exploited, this time to derive the magnetic field which would be consistent with the obtained distributions. Comparison of the derived field with the one used for tracing showed that pressure balance is almost maintained. The pressure imbalance is weak, yet this imbalance is responsible for the temporal variability of the shock behind the ramp. We went even further and compared our hybrid simulations with the results of ion tracing in a completely analytically modelled shock profile, while retaining only the most important feature (overshoot) and the basic shock parameters as in the simulation. Each of these two steps takes us further away from the self-consistent picture obtained within the hybrid simulation. Therefore one could expect progressively worse agreement between the ion distributions and magnetic fields obtained with tracing and those found in the hybrid simulation. Yet, the agreement remained rather good even for the modelled shocks. Recently, the results of a test particle ion tracing have been compared (Gedalin Reference Gedalin2019b ) with an observed interplanetary supercritical shock observed by MMS (magnetospheric multiscale mission) on 2018-01-08 (Cohen et al. Reference Cohen, Schwartz, Goodrich, Ahmadi, Ergun, Fuselier, Desai, Christian, McComas and Zank2019). The comparison has shown good agreement. These findings show that (a) the macroscopic fields play the main role in the formation of downstream ion distributions and the magnetic profile of the shock, (b) the time dependence of the analysed moderately supercritical shock with ion reflection is clear but weak and (c) the shock non-stationarity is directly related to the pressure imbalance. The latter means that, in principle, temporal evolution of the shock profiles may be described within the time-dependent conservation-law approach (to be developed). Applicability of the proposed approach to higher Mach number shocks is yet to be explored.
No new dataset was produced in this study. The magnetic field data were taken from the CLUSTER Science Archive https://csa.esac.esa.int/csa-web/. Hybrid simulations have been performed using dHybrid code. The wavelet transform used the Wavelab package https://statweb.stanford.edu/∼wavelab/.














