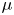In recent years, charged particles acceleration by plasma wakefields has attracted great interest. One of the most attractive advantages of the plasma wakefield is the large acceleration gradient. For plasma with a density of $10^{18}\ {\rm cm}^{-3}$, the typical amplitude of acceleration field $E_{0}$ can reach approximately 100 GV m$^{-1}$ according to the wave breaking limit (Dawson Reference Dawson1959; Lotov Reference Lotov2010), making it possible to accelerate charged particles to relativistic energy within an ultrashort length. When an intense pulsed laser or a relativistic particle beam interacts with plasma, a plasma wakefield can be excited and used to accelerate charged particles, known as LWFA (Laser wakefield accelerator) (Tajima & Dawson Reference Tajima and Dawson1979; Pukhov & Meyer ter Vehn Reference Pukhov and Meyer ter Vehn2002) or PWFA (Plasma wakefield accelerator) (Chen et al. Reference Chen, Dawson, Huff and Katsouleas1985), respectively. In the past few decades, both the LWFA and PWFA have been widely studied in electron acceleration (Pukhov, Sheng & Meyer ter Vehn Reference Pukhov, Sheng and Meyer ter Vehn1999; Blumenfeld et al. Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Wang et al. Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa and Tsai2013; Litos et al. Reference Litos, Adli, Allen, An, Clarke, Corde, Clayton, Frederico, Gessner and Green2016; Gonsalves et al. Reference Gonsalves, Nakamura, Daniels, Benedetti, Pieronek, de Raadt, Steinke, Bin, Bulanov and van Tilborg2019; Rosmej et al. Reference Rosmej, Gyrdymov, Günther, Andreev, Tavana, Neumayer, Zähter, Zahn, Popov and Borisenko2020), and much progress has already been made. At the same time, the interaction of pulsed laser with high density plasma has also been used to accelerate ions (Qiao et al. Reference Qiao, Zepf, Borghesi and Geissler2009; Liu et al. Reference Liu, Qu, Liu, Li, Cai, Tang and Kong2020). These energetic ions have wide applications, such as astrophysics (Remington et al. Reference Remington, Drake, Takabe and Arnett2000), proton radiography (King et al. Reference King, Ables, Adams, Alrick, Amann, Balzar, Barnes, Crow, Cushing and Eddleman1999), tumour therapy (Bulanov & Khoroshkov Reference Bulanov and Khoroshkov2002) and fast ignition (Roth et al. Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely and Wilks2001). At present, many ion acceleration schemes based on pulsed laser–plasma interaction have been developed, such as target normal sheath acceleration (TNSA) (Maksimchuk et al. Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000; Snavely et al. Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster and Singh2000; Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001), radiation-pressure acceleration (RPA) (Esirkepov et al. Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Macchi et al. Reference Macchi, Cattani, Liseykina and Cornolti2005; Robinson et al. Reference Robinson, Zepf, Kar, Evans and Bellei2008; Yan et al. Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen2008; Macchi, Veghini & Pegoraro Reference Macchi, Veghini and Pegoraro2009; Qiao et al. Reference Qiao, Zepf, Borghesi and Geissler2009; Shen et al. Reference Shen, Qiao, Zhang, Kar, Zhou, Chang, Borghesi and He2017), shockwave acceleration (Fiuza et al. Reference Fiuza, Stockem, Boella, Fonseca, Silva, Haberberger, Tochitsky, Gong, Mori and Joshi2012; Zhang et al. Reference Zhang, Qiao, Huang, Shen, You, Yan, Wu, Zhou and He2016), peeler acceleration (Shen, Pukhov & Qiao Reference Shen, Pukhov and Qiao2021), cascaded acceleration (Gonoskov et al. Reference Gonoskov, Korzhimanov, Eremin, Kim and Sergeev2009; He et al. Reference He, Qiao, Shen, Yao, Yao, Zhou, He, Zhu, Pei and Fu2019) and the breakout afterburner scheme (Yin et al. Reference Yin, Albright, Hegelich and Fernández2006,  Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernández2007).

Compared with LWFA, using the PWFA scheme to accelerate electrons can reduce the influence caused by phase slippage, so that it is easier to achieve stable long-range acceleration (Shin Reference Shin2014). At the same time, it is possible to take advantage of the high-energy electron beams generated by the traditional accelerators that have already been built (Blumenfeld et al. Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas and Kirby2007; Litos et al. Reference Litos, Adli, An, Clarke, Clayton, Corde, Delahaye, England, Fisher and Frederico2014,  Reference Litos, Adli, Allen, An, Clarke, Corde, Clayton, Frederico, Gessner and Green2016) around the world. However, the investigations on the use of PWFA to accelerate ions are relatively few, to date. In this paper, we propose a new proton acceleration scheme by the interaction of a relativistic electron beam with an underdense plasma slab. As our two-dimensional (2-D) particle-in-cell (PIC) simulations show, when the electron driving beam travels into the middle of the plasma slab, a wakefield can be excited, as in the well known bubble regime. After the driving beam has propagated through the plasma region, a bunch of proton beams can be pulled out following the driving beam, similar to the TNSA scheme in the laser-driven proton acceleration. Then these protons can be accelerated continuously to energies up to several hundreds of MeV in vacuum. In the absence of superpulsed lasers, it would make sense to obtain high-energy protons using the mechanism proposed in this paper. In the following, the physics behind this acceleration scheme is discussed in detail.

In general, when a high-power pulsed laser beam propagates into a plasma, it can excite a linear or nonlinear wakefield, depending on the intensity of the laser (Lu et al. Reference Lu, Huang, Zhou, Mori and Katsouleas2005). The situation is similar when the driving beam is a relativistic electron beam. When a relativistic electron beam with low charge value propagates into an underdense plasma, a linear wakefield will be formed. If the driving beam has a high charge value and high density, the linear wakefield will turn into a nonlinear wakefield, and this case is also called the bubble region (Lu et al. Reference Lu, Huang, Zhou, Tzoufras, Tsung, Mori and Katsouleas2006). As a typical case in our 2-D simulation, a bi-Gaussian driving beam is incident from the left-hand of the simulation box along the $x$ direction. In the case of using the EPOCH ‘injector’ module, the density profile of the driving beam can be described as

(0.1)\begin{equation} n_{b}=n_{b0}\exp\left[-\frac{r^{2}}{2\sigma_{r}^{2}}- \frac{(t-3\sigma_{t0})^{2}}{2\sigma_{t0}^{2}} \right], \end{equation}

where $\sigma _{t0}=80.0\ \mathrm {\mu }{\rm m}\ c^{-1}$; $\sigma _{r}=4.22/k_{p}=10.0\ \mathrm {\mu }$m; $k_{p}=\sqrt {n_{0}e^{2}/(\varepsilon _{0}m_{e}c^{2})}$ is the plasma wavenumber; $n_{0}=5.0\times 10^{18}\ {\rm cm}^{-3}$ is the plasma density; $e$, $m_{e}$ and $c$ are the charge value of a unit charge, the rest mass of an electron and the speed of light, respectively. The longitudinal distribution of the driving beam is controlled by the time parameters $t$ and $\sigma _{t0}$. The initial energy of the driving beam is 1.0 GeV per particle, and its peak density is $n_{b0}=4.0\times 10^{18}\ {\rm cm}^{-3}$. The charge value of the driving beam is approximately 3.19 nC $\mathrm {\mu }{\rm m}^{-1}$. The 2-D simulations were carried out using the PIC code EPOCH (Arber et al. Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015). The ‘simple outflow’ boundary conditions are used on the simulation box front and back boundary, and the lateral boundary conditions are ‘open’. The simulation box is a rectangular area of $1500\ \mathrm {\mu }{\rm m}\times 800\ \mathrm {\mu }$m which has 7500 grids in the $x$ direction and 4000 grids in the $y$ directions, and four superparticles per cell for each particle species. The plasma slab is composed of electrons and protons ranging from $x=600 \ \mathrm {\mu }$m to $x=800 \ \mathrm {\mu }$m, and it is composed of a $30 \ \mathrm {\mu }$m up-ramp region and a $170 \ \mathrm {\mu }$m platform region. In the density up-ramp transitional region ($x=600$–$630\ \mathrm {\mu }$m), plasma density increases linearly from 0.5$n_{0}$ to $n_{0}$; in the platform region ($x=630$–$800\ \mathrm {\mu }$m), plasma density keeps constant $n_{0}$. The schematic diagram of the PIC simulation box is shown in figure 1. As is shown in this figure, the relativistic electron beam is represented by a red ellipse.

Figure 1. Schematic diagram of the 2-D PIC simulation box and the plasma density profiles $n_{p}$. The driver beam is represented by a red ellipse.

To clearly describe the interaction process of the relativistic electron beam with plasma, we present the electron and proton number density of the typical 2-D simulation case at different specific moments (t = 3100 fs, 4400 fs and 6800 fs) in figure 2, where figure 2(a–c) show the electron number density and figure 2(d–f ) show the proton number density. The number density value is represented by the colourbar and has been normalized with $n_{0}$. As mentioned above, since the driving beam has a high charge value and energy, when the driving beam moves into the plasma slab, the background electrons are pushed away laterally by the expelling force of the driving beam. Therefore, an electron bubble is formed as shown in figure 2(a). At this time, figure 2(d) shows that the background protons are also disturbed, but these protons do not have a large displacement because the mass of a proton is much larger than that of an electron. If the length of the plasma target is long enough, the bubble will move following the driving beam while the driving beam will lose energy continuously. This scheme may enter a process of electron acceleration in the bubble. However, if the plasma length is limited to a reasonably small value, such as the bubble length, the driving beam will quickly pass through the plasma region. As a result, the plasma bubble cannot remain closed for a long time. Since the plasma density is higher than the driving beam density, the background electrons can be quickly pulled back by the positively charged ions. Therefore, the plasma bubble is relatively small, as expected. In figures 2(b) and 2(e), one can see that the driving beam has passed through the plasma slab at $t = 4400$ fs, a low-density channel-like structure is formed in the middle of the plasma region, and a bunch of protons has rushed out of the right-hand boundary of the plasma slab into the vacuum at the same time. It should be noted that the profile of the driving beam has evolved from a Gaussian shape to a fish-like shape which has a fishtail-like structure at its rear. After that, the driving beam leaves the plasma with a velocity very close to the speed of light in a vacuum, just as shown in figure 2(c). Meanwhile, the background plasma electrons at 6800 fs, which do not have enough energy to catch up with the driving beam and the high-energy proton beam, stay in the region around the plasma slab and form an electron cloud. In figure 2(f), the accelerated protons have also moved farther from the right-hand boundary of the plasma region and form a proton bunch with good collimation.

Figure 2. Panels (a–c) show the number density of the background electrons and the driving beam at $t = 3100$ fs, 4400 fs and 6800 fs, respectively. Panels (d–f) are the number density of the background protons at $t = 3100$ fs, 4400 fs and 6800 fs, respectively. The number density value is displayed by the colourbar and has been normalized with the background plasma density $n_{0}$.

To give a more detailed study on the proton acceleration mechanism, we plot the longitudinal electric field on the central axis $r=0$ (represented by the blue line) and the driving beam (represented by a purple block) at different times in figure 3. Dotted black lines indicate the initial left-hand and right-hand boundaries of the plasma slab. Apart from this, protons with energy greater than 50 MeV at 7500 fs are tracked and drawn in these diagrams, and the unit of the colourbar representing the energy of the tracked protons is MeV. At 3100 fs, one can see that the longitudinal electric field $E_{x}$ in figure 3(a) is similar to the wakefield in a plasma bubble, and the peak value of the positive field is approximately 5 GV cm$^{-1}$. All traced protons are located near the right-hand boundary of the plasma slab, and their energy is not greater than 1.0 MeV. This means that the protons at this time have not been accelerated yet. However, as the main part of the driving beam rushes out of the right-hand boundary of the plasma, the positive electric field peak value quickly increased to around 15.0 GV cm$^{-1}$, as shown in figure 3(b). This phenomenon is because the charge of the driving beam is concentrated in a small area and the driving beam is very close to the positively charged ion area in plasma. At this moment, a strong charge separation field is formed. The positive field coming from the driving beam superposition with the charge separation field forms an enhanced acceleration field which can accelerate the traced protons violently. At 3700 fs, some of the traced protons have been accelerated to approximately 20 MeV. At 4400 fs, the maximum energy of these protons has exceeded 100 MeV, as shown in figure 3(c). From this figure, it can be seen that the amplitude of the positive longitudinal field has decreased but is still greater than 6 GV cm$^{-1}$. The strong longitudinal field can accelerate protons quickly, just like the field in the TNSA scheme. Compared with the TNSA scheme driven by a pulsed laser, the electron driving beam has small energy spread, good collimation and higher energy, so it is expected to obtain a higher quality accelerated proton beam in this scheme. The following analyses show that the accelerated protons do have good collimation and high energy. After the driving beam has rushed out from the plasma slab completely, the rear of the driving beam evolves into a fishtail shape, and there is an electric field peak appearing at the place where the tail of the driving beam and the head of the traced proton beam overlap. It is worth mentioning that the fishtail structure forms a flat distribution of longitudinal electric field along the transverse direction, which can also lead to better collimation compared with that of the TNSA scheme.

Figure 3. The longitudinal electric field along $y=0$ (represented by the blue lines) and the electron driver beam (represented by a purple block) at 3100 fs (a), 3700 fs (b), 4400 fs (c) and 6800 fs (d), respectively. At the same time, the space–energy distribution of the protons with energy greater than 50 MeV at 7500 fs are also drawn in these diagrams, and the unit of the colourbar is MeV.

Thereafter, the proton beam and driving beam form a two-stream instability structure, and the protons undergo a long-range acceleration process. As shown in figure 3(d), the peak of $E_{x}$ has decreased to 3.4 GV cm$^{-1}$ at 6800 fs, but the longitudinal distribution length of the positive field has also become longer, and the proton beam is still located in an acceleration phase. At the position of the driving beam, there is a longitudinal electric field of approximately 2.4 GV cm$^{-1}$. There are two main sources of this longitudinal electric field, one of which is the lateral movement of the driving beam electrons. It is impossible for any energy electron beam in vacuum to remain collimated and so it must expand laterally. This will generate an $E_{y}$. The second part is the charge separation field between the driving beam and the accelerated protons, although it is much smaller than before. The superposition of these two electric fields results in the 2.4 GV cm$^{-1}$ longitudinal electric field at the position of the driving beam. Because the speed of protons is smaller than that of the driving beam, the accelerated protons will gradually slip backward relative to the driving beam. As the longitudinal field $E_{x}$ on the central axis becomes weaker, the energy increase of the accelerated protons will become slow. This long-range acceleration process can last a long time until the distance between the proton beam and the driving beam is too large to maintain a strong acceleration field for protons or the driving beam collapses. Figure 3(d) also shows that the maximum energy of the traced protons has exceeded 200 MeV.

In order to analyse the beam quality of the accelerated proton beam in our scheme, we plot the space–energy distribution of protons emitted from the plasma slab, the energy spectrum, and the angular spectrum of protons with energy greater than 100 MeV at 7500 fs in figure 4. The colourmap in figure 4(a) shows the proton energy value, and the units of colourbar are MeV. From this figure, it is easy to find that most of the protons with energy greater than 100 MeV are distributed in $x=1100$–$1500\ \mathrm {\mu }$m, and the protons with the maximum energy are distributed in the head part of the accelerated proton beam. Figure 4(b) presents the energy spectrum of the protons with energy greater than 100 MeV at $t = 7500$ fs. It can be found that the maximum proton energy $E_{max}$ is close to 300 MeV. The angular spectrum of the accelerated protons is shown in figure 4(c). From this figure, one can find that the divergence angle of the protons has two peaks at $\theta =9^{\circ }$ and $\theta =-9^{\circ }$. The normalized emittance of the protons with energy greater than 100.0 MeV at $t = 7500$ fs is $\varepsilon _{p,rms}=0.46\pi$ mm mrad, calculated by Floettmann (Reference Floettmann2003),

(0.2)\begin{equation} \varepsilon_{p,rms}=\frac{1}{m_{p}c}\sqrt{\langle y^{2}\rangle \langle p_{y}^{2}\rangle-\langle yp_{y}\rangle^{2}},\end{equation}

where $m_{p}$ is the rest mass of the proton. This result means that this proton beam has good collimation. What is more, the charge value of the protons with energy greater than 100.0 MeV is approximately 0.46 nC $\mathrm {\mu }{\rm m}^{-1}$. As mentioned above, the proton acceleration process can be divided into two stages: the TNSA-like acceleration stage and the long-range acceleration stage, which are further confirmed by the following analyses in figure 5. The temporal evolution of the maximum energy of the accelerated protons $E_{max}$ is shown in figure 5(a). Before 3200 fs, the background protons do not gain energy. From 3200 fs, some protons start to be accelerated, especially from 3600 fs to 4600 fs, $E_{max}$ increases from 18.6 MeV to 118.0 MeV quickly. Combined with the discussion above, this stage belongs to a scheme of TNSA-like acceleration. In $5000\ {\rm fs}$–$7000\ {\rm fs}$, the growth of $E_{max}$ slowed down, and this is consistent with the long-range acceleration process. After 2000 fs acceleration, $E_{max}$ is still able to increase from approximately 120 MeV to 268 MeV. The two red dotted lines $L_{1}$ and $L_{2}$ in figure 5(a) represent the linear fit of $E_{max}$ in these two stages. It can be seen that the energy increase rate of the first stage is approximately two times that of the second stage. In figure 5(b), the evolution of energy loss percentage $\eta$ over time is presented, and $\eta$ is defined as the lost energy divided by the initial total energy of the driving beam. This figure also indicates that $\eta$ is different in two acceleration stages. The two red dotted lines $L_{1}$ and $L_{2}$ in figure 5(b) show the linear fit of $\eta$ in two stages. The slopes of $L_{1}$ and $L_{2}$ indicate that the energy lost speed in the first stage is larger than twice that of the second stage, inferring that when the driving beam just rushes out of the plasma boundary energy can be transferred rapidly from the driving beam to the background protons. In the second acceleration stage, the energy conversion rate starts to slow down. From figure 5(b), one can see the remaining energy of the driving beam is approximately $50\,\%$ at 7000 fs. In addition, it is found that $14.2\,\%$ of the energy of the driving beam is converted into the kinetic energy of the accelerated proton beam at 7000 fs. Thereafter, the acceleration field weakens with the increase of distance between two streams and this is the most critical reason in the termination of proton acceleration. From the above results it can be seen that the energy conversion efficiency from the driving beam to protons still has great potential for improvement; to find some ideas to improve the energy transfer ratio requires further investigations. Besides, it should be noted that the proton acceleration mechanism proposed in this paper relies on a driving beam generation method with large charge value. Perhaps an intense laser interacting with a near-critical plasma density could produce an electron beam with such a large charge.

Figure 4. The analyses of the accelerated proton beam. Panel (a) shows the space–energy distribution of protons at $t = 7500$ fs. The unit of the colourbar is MeV. Panels (b) and (c) are the energy spectrum and angular spectrum of protons with energy greater than 100 MeV at $t = 7500$ fs, respectively.

Figure 5. (a) The temporal evolution of the maximum energy $E_{max}$ of the accelerated protons. (b) The temporal evolution of the energy loss percentage $\eta$ of the driving beam. The red dotted lines $L_{1}$ and $L_{2}$ represent the linear fit to the data in (a) and (b).

In summary, we proposed a proton acceleration scheme through the interaction of a high-energy electron beam with an underdense plasma slab. Our simulations show that the protons can be accelerated by a TNSA-like process, followed by a long-range acceleration mechanism. The accelerated protons can obtain energy up to approximately 250 MeV within a period of around 4000 fs acceleration by an electron driving beam with an energy of 1.0 GeV per particle. Compared with protons accelerated by the TNSA scheme, the proton beam accelerated by the electron driving beam has good beam quality, high energy and good collimation. The proton acceleration scheme proposed in this paper provides a new way to generate high energy protons or ions and may be used for nuclear fusion and material treatment.