Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T02:15:22.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Hall instability: origin, properties and asymptotic theory for its tearing mode

Published online by Cambridge University Press:  14 July 2021

Leonid Kitchatinov Open the ORCID record for Leonid Kitchatinov [Opens in a new window]
Leonid Kitchatinov*
Affiliation:
Institute of Solar-Terrestrial Physics SB RAS, Lermontov Str. 126A, 664033Irkutsk, Russia Pulkovo Astronomical Observatory, St. Petersburg196140, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hall instability in electron magnetohydrodynamics is interpreted as the shear-Hall instability driven jointly by helicoidal oscillations and shear in the electron current velocity. This explanation suggests an antiparallel orientation of the background magnetic field and vorticity of the current velocity as the necessary condition for Hall instability. The condition is tested and generally confirmed by numerical computations in plane slab geometry. Unstable eigenmodes are localized in the spatial regions of the antiparallel field and vorticity. Computations of the tearing-type mode of the instability are complemented by (and generally agree with) asymptotic analytical estimations for large Hall numbers. The stabilizing effect of perfect conductor boundary conditions is found and explained. For large Hall numbers, the growth rates approach the power-law dependence $\sigma \propto B^\alpha \eta ^{1-\alpha }$ on the magnetic field ($B$) and diffusivity ($\eta$). 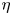Almost all computations give the power index $\alpha = 3/4$ 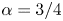with one exception of the tearing-type mode with vacuum boundary conditions for which case $\alpha = 2/3$.

Keywords

astrophysical plasmasplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 4 , August 2021 , 905870404
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bora, K., Bhattacharyya, R. & Smolarkiewicz, P.K. 2021 Evolution of three-dimensional coherent structures in hall magnetohydrodynamics. Astrophys. J. 906 (2), 102.CrossRefGoogle Scholar
Brandenburg, A. 2020 Hall cascade with fractional magnetic helicity in neutron star crusts. Astrophys. J. 901 (1), 18.CrossRefGoogle Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417 (1-4), 1–209.CrossRefGoogle Scholar
Furth, H.P., Killeen, J. & Rosenbluth, M.N. 1963 Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6 (4), 459–484.CrossRefGoogle Scholar
Goldreich, P. & Reisenegger, A. 1992 Magnetic field decay in isolated neutron stars. Astrophys. J. 395, 250–258.CrossRefGoogle Scholar
Gourgouliatos, K.N. & Hollerbach, R. 2016 Resistive tearing instability in electron MHD: application to neutron star crusts. Mon. Not. R. Astron. Soc. 463 (3), 3381–3389.CrossRefGoogle Scholar
Hollerbach, R. & Rüdiger, G. 2002 The influence of Hall drift on the magnetic fields of neutron stars. Mon. Not. R. Astron. Soc. 337 (1), 216–224.CrossRefGoogle Scholar
Kitchatinov, L. 2019 Stability of a force-free Hall equilibrium and release of magnetic energy. Astron. Nachr. 340 (6), 475–482.CrossRefGoogle Scholar
Kitchatinov, L.L. 2017 Double Hall instability: a catalyzer of magnetic energy release. Astron. Lett. 43 (9), 624–633.CrossRefGoogle Scholar
Kunz, M.W. 2008 On the linear stability of weakly ionized, magnetized planar shear flows. Mon. Not. R. Astron. Soc. 385 (3), 1494–1510.CrossRefGoogle Scholar
Parker, E.N. 1979 Cosmical Magnetic Fields: Their Origin and Their Activity. Clarendon Press.Google Scholar
Pons, J.A. & Geppert, U. 2010 Confirmation of the occurrence of the Hall instability in the non-linear regime. Astron. Astrophys. 513, L12.CrossRefGoogle Scholar
Priest, E. 2014 Magnetohydrodynamics of the Sun. Cambridge University Press.Google Scholar
Rheinhardt, M. & Geppert, U. 2002 Hall-drift induced magnetic field instability in neutron stars. Phys. Rev. Lett. 88 (10), 101103.CrossRefGoogle ScholarPubMed
Rheinhardt, M., Konenkov, D. & Geppert, U. 2004 The occurrence of the Hall instability in crusts of isolated neutron stars. Astron. Astrophys. 420, 631–645.CrossRefGoogle Scholar
Rüdiger, G. & Hollerbach, R. 2004 The Magnetic Universe: Geophysical and Astrophysical Dynamo Theory. Wiley-VCH.CrossRefGoogle Scholar
Rüdiger, G. & Kitchatinov, L.L. 2005 The influence of the Hall effect on the global stability of cool protostellar disks. Astron. Astrophys. 434 (2), 629–635.CrossRefGoogle Scholar
Shi, C., Velli, M., Pucci, F., Tenerani, A. & Innocenti, M.E. 2020 Oblique tearing mode instability: guide field and hall effect. Astrophys. J. 902 (2), 142.CrossRefGoogle Scholar
Somov, B.V. 2013 Plasma Astrophysics, Part I. Springer Science+Business Media.CrossRefGoogle Scholar
Vainshtein, S.I., Chitre, S.M. & Olinto, A.V. 2000 Rapid dissipation of magnetic fields due to the Hall current. Phys. Rev. E 61 (4), 4422–4430.CrossRefGoogle ScholarPubMed
Wood, T.S., Hollerbach, R. & Lyutikov, M. 2014 Density-shear instability in electron magneto-hydrodynamics. Phys. Plasmas 21 (5), 052110.CrossRefGoogle Scholar
Zhang, W., Ma, Z.W. & Wang, S. 2017 Hall effect on tearing mode instabilities in tokamak. Phys. Plasmas 24 (10), 102510.CrossRefGoogle Scholar