Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T02:15:46.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Gradient-based optimization of 3D MHD equilibria

Part of: Focus on Fusion

Published online by Cambridge University Press:  05 April 2021

Elizabeth J. Paul Open the ORCID record for Elizabeth J. Paul [Opens in a new window] ,
Matt Landreman Open the ORCID record for Matt Landreman [Opens in a new window]  and
Thomas Antonsen Jr. Open the ORCID record for Thomas Antonsen Jr. [Opens in a new window]
Elizabeth J. Paul*
Affiliation:
Department of Astrophysical Sciences, Princeton University, Princeton, NJ08544, USA
Matt Landreman
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD20742, USA
Thomas Antonsen Jr.
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD20742, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using recently developed adjoint methods for computing the shape derivatives of functions that depend on magnetohydrodynamic (MHD) equilibria (Antonsen et al., J. Plasma Phys., vol. 85, issue 2, 2019; Paul et al., J. Plasma Phys., vol. 86, issue 1, 2020), we present the first example of analytic gradient-based optimization of fixed-boundary stellarator equilibria. We take advantage of gradient information to optimize figures of merit of relevance for stellarator design, including the rotational transform, magnetic well and quasi-symmetry near the axis. 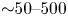With the application of the adjoint method, we reduce the number of equilibrium evaluations by the dimension of the optimization space (${\sim }50\text {--}500$) in comparison with a finite-difference gradient-based method. We discuss regularization objectives of relevance for fixed-boundary optimization, including a novel method that prevents self-intersection of the plasma boundary. We present several optimized equilibria, including a vacuum field with very low magnetic shear throughout the volume.

Keywords

fusion plasmaplasma confinementplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 2 , April 2021 , 905870214
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, F. S. B., Almagri, A. F., Anderson, D. T., Matthews, P. G., Talmadge, J. N. & Shohet, J. L. 1995 The Helically Symmetric eXperiment, (HSX) goals, design and status. Fusion Technol. 27 (3T), 273–277.CrossRefGoogle Scholar
Antonsen, T., Paul, E. J. & Landreman, M. 2019 Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. J. Plasma Phys. 85 (2), 905850207.CrossRefGoogle Scholar
Beidler, C., Grieger, G., Herrnegger, F., Harmeyer, E., Kisslinger, J., Lotz, W., Maassberg, H., Merkel, P., Nührenberg, J., Rau, F., et al. 1990 Physics and engineering design for Wendelstein VII-X. Fusion Technol. 17 (1), 148–168.CrossRefGoogle Scholar
Carlen, M., Laurie, B., Maddocks, J. H. & Smutny, J. 2005 Biarcs, global radius of curvature, and the computation of ideal knot shapes. In Physical and Numerical Models in Knot Theory: Including Applications to the Life Sciences, pp. 75–108. World Scientific.CrossRefGoogle Scholar
Carlton-Jones, A., Paul, E. J. & Dorland, W. 2020 Computing the shape gradient of stellarator coil complexity with respect to the plasma boundary. J. Plasma Phys. arXiv:2011.03702.Google Scholar
Castellano, J., Jiménez, J. A., Hidalgo, C., Pedrosa, M. A., Fraguas, A. L., Pastor, I., Herranz, J., Alejaldre, C. & TJ-II Team 2002 Magnetic well and instability thresholds in the TJ-II stellarator. Phys. Plasmas 9 (2), 713–716.CrossRefGoogle Scholar
Cooper, W. A., Hirshman, S. P., Merazzi, S. & Gruber, R. 1992 3D magnetohydrodynamic equilibria with anisotropic pressure. Comput. Phys. Commun. 72 (1), 1.CrossRefGoogle Scholar
Dekeyser, W. 2014 Optimal plasma edge configurations for next-step fusion reactors. PhD thesis, Katholieke Universiteit Leuven.Google Scholar
Drevlak, M., Beidler, C. D., Geiger, J., Helander, P. & Turkin, Y. 2018 Optimisation of stellarator equilibria with ROSE. Nucl. Fusion 59 (1), 016010.CrossRefGoogle Scholar
Drevlak, M., Brochard, F., Helander, P., Kisslinger, J., Mikhailov, M., Nührenberg, C., Nührenberg, J. & Turkin, Y. 2013 ESTELL: a quasi-toroidally symmetric stellarator. Contrib. Plasma Phys. 53 (6), 459–468.CrossRefGoogle Scholar
Drevlak, M. C., Geiger, J., Helander, P. & Turkin, Y. 2014 Fast particle confinement with optimized coil currents in the W7-X stellarator. Nucl. Fusion 54 (7), 073002.CrossRefGoogle Scholar
Emmerich, M., Giotis, A., Özdemir, M., Bäck, T. & Giannakoglou, K. 2002 Metamodel-assisted evolution strategies. In International Conference on Parallel Problem Solving From Nature, pp. 361–370. Springer.CrossRefGoogle Scholar
Gelsey, A. 1995 Intelligent automated quality control for computational simulation. AI EDAM 9 (5), 387–400.Google Scholar
Gelsey, A., Schwabacher, M. & Smith, D. 1998 Using modeling knowledge to guide design space search. Artif. Intell. 101 (1–2), 35–62.CrossRefGoogle Scholar
Giuliani, A., Wechsung, F., Cerfon, A., Stadler, G. & Landreman, M. 2020 Single-stage gradient-based stellarator coil design: optimization for near-axis quasi-symmetry. arXiv:2010.02033.Google Scholar
Gonzalez, O. & Maddocks, J. H. 1999 Global curvature, thickness, and the ideal shapes of knots. Proc. Natl Acad. Sci. 96 (9), 4769–4773.CrossRefGoogle ScholarPubMed
Greene, J. M., MacKay, R. S. & Stark, J. 1986 Boundary circles for area-preserving maps. Physica D 21 (2–3), 267–295.CrossRefGoogle Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.CrossRefGoogle ScholarPubMed
Henneberg, S. A., Drevlak, M., Nührenberg, C., Beidler, C. D., Turkin, Y., Loizu, J. & Helander, P. 2019 Properties of a new quasi-axisymmetric configuration. Nucl. Fusion 59 (2), 026014.CrossRefGoogle Scholar
Hirshman, S. P. & Whitson, J. C. 1983 Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553–3568.CrossRefGoogle Scholar
Hudson, S. R., Dewar, R. L., Dennis, G., Hole, M. J., McGann, M., Von Nessi, G. & Lazerson, S. 2012 Computation of multi-region relaxed magnetohydrodynamic equilibria. Phys. Plasmas 19 (11), 112502.CrossRefGoogle Scholar
Johnson, S. G. 2014 The NLopt nonlinear-optimization package, http://github.com/stevengj/nlopt.Google Scholar
Kesner, J., Ramos, J. J. & Gang, F.-Y. 1995 Comet cross-section tokamaks. J. Fusion Energy 14 (4), 361–371.CrossRefGoogle Scholar
Landreman, M. 2021 Figures of merit for stellarators near the magnetic axis. J. Plasma Phys. 87 (1), 905870112.CrossRefGoogle Scholar
Landreman, M. & Jorge, R. 2020 Magnetic well and Mercier stability of stellarators near the magnetic axis. J. Plasma Phys. 86 (5), 905860510.CrossRefGoogle Scholar
Landreman, M. & Sengupta, W. 2019 Constructing stellarators with quasisymmetry to high order. J. Plasma Phys. 85 (6), 815850601.CrossRefGoogle Scholar
Lazerson, S., Schmitt, J., Zhu, C. & STELLOPT Developers 2020 STELLOPT. https://github.com/PrincetonUniversity/STELLOPT.Google Scholar
Lemaréchal, C. 1982 Numerical experiments in nonsmooth optimization. IIASA Workshop on Progress in Non-differentiable Optimization. 61–84. Laxenburg, Austria.Google Scholar
Lewis, A. S. & Overton, M. L. 2013 Nonsmooth optimization via quasi-newton methods. Math. Program. 141 (1), 135–163.CrossRefGoogle Scholar
McGreivy, N., Hudson, S. R. & Zhu, C. 2021 Optimized finite-build stellarator coils using automatic differentiation. Nucl. Fusion 61 (2), 026020.CrossRefGoogle Scholar
Medvedev, S. Y., Kikuchi, M., Villard, L., Takizuka, T., Diamond, P., Zushi, H., Nagasaki, K., Duan, X., Wu, Y., Ivanov, A. A., et al. 2015 The negative triangularity tokamak: stability limits and prospects as a fusion energy system. Nucl. Fusion 55 (6), 063013.CrossRefGoogle Scholar
Meiss, J. D. 1992 Symplectic maps, variational principles, and transport. Rev. Mod. Phys. 64 (3), 795.CrossRefGoogle Scholar
Mercier, C. 1964 Equilibrium and stability of a toroidal magnetohydrodynamic system in the neighbourhood of a magnetic axis. Nucl. Fusion 4 (3), 213.CrossRefGoogle Scholar
Mercier, C. & Luc, H. 1974 The MHD approach to the problem of plasma confinement in closed magnetic configurations. Lectures in Plasma Physics. Commission of the European Communities.Google Scholar
Miner, W. H. Jr., Valanju, P. M., Hirshman, S. P., Brooks, A. & Pomphrey, N. 2001 Use of a genetic algorithm for compact stellarator coil design. Nucl. Fusion 41 (9), 1185.CrossRefGoogle Scholar
Mynick, H. E., Pomphrey, N. & Ethier, S. 2002 Exploration of stellarator configuration space with global search methods. Phys. Plasmas 9 (3), 869–876.CrossRefGoogle Scholar
Nocedal, J. & Wright, S. J. 2006 Numerical Optimization. Springer.Google Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129 (2), 113–117.CrossRefGoogle Scholar
Oymak, S. & Soltanolkotabi, M. 2018 Overparameterized nonlinear learning: gradient descent takes the shortest path? arXiv:1812.10004.Google Scholar
Paul, E. J. 2020 Adjoint methods for stellarator shape optimization and sensitivity analysis. arXiv:2005.07633.Google Scholar
Paul, E. J., Abel, I. G., Landreman, M. & Dorland, W. 2019 An adjoint method for neoclassical stellarator optimization. J. Plasma Phys. 85 (5), 795850501.CrossRefGoogle Scholar
Paul, E. J., Antonsen, T., Landreman, M. & Cooper, W. A. 2020 Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. Part 2. Applications. J. Plasma Phys. 86 (1), 905860103.CrossRefGoogle Scholar
Paul, E. J., Landreman, M., Bader, A. & Dorland, W. 2018 An adjoint method for gradient-based optimization of stellarator coil shapes. Nucl. Fusion 58 (7), 076015.CrossRefGoogle Scholar
Pogutse, O. & Yurchenko, E. 1982 Reviews of Plasma Physics. Consultants Bureau.Google Scholar
Rasheed, K., Hirsh, H. & Gelsey, A. 1997 A genetic algorithm for continuous design space search. Artif. Intell. Eng. 11 (3), 295–305.CrossRefGoogle Scholar
Rodriguez, E., Helander, P. & Bhattacharjee, A. 2020 Necessary and sufficient conditions for quasisymmetry. Phys. Plasmas 27 (6), 062501.CrossRefGoogle Scholar
Sanchez, R., Hirshman, S. P., Ware, A. S., Berry, L. A. & Spong, D. A. 2000 Ballooning stability optimization of low-aspect-ratio stellarators. Plasma Phys. Control. Fusion 42 (6), 641.CrossRefGoogle Scholar
Sauer, T. 2012 Numerical Analysis. Pearson.Google Scholar
Smutny, J. 2004 Global radii of curvature, and the biarc approximation of space curves: in pursuit of ideal knot shapes. PhD thesis, EPFL.Google Scholar
Taylor, J. B. 1965 Simple toroidal magnetic field with negative $V''$. Phys. Fluids 8 (6), 1203–1205.CrossRefGoogle Scholar
Walker, S. W. 2016 Shape optimization of self-avoiding curves. J. Comput. Phys. 311, 275–298.CrossRefGoogle Scholar
Watanabe, K. Y., Sakakibara, S., Narushima, Y., Funaba, H., Narihara, K., Tanaka, K., Yamaguchi, T., Toi, K., Ohdachi, S., Kaneko, O., et al. 2005 Effects of global MHD instability on operational high beta-regime in LHD. Nucl. Fusion 45 (11), 1247.CrossRefGoogle Scholar
Wesson, J. & Campbell, D. J. 2011 Tokamaks. International Series of Monographs on Physics, vol. 149. Oxford University Press.Google Scholar
Zarnstorff, M. C., Berry, L. A., Brooks, A., Fredrickson, E., Fu, G. Y., Hirshman, S., Hudson, S., Ku, L. P., Lazarus, E., Mikkelsen, D., et al. 2001 Physics of the compact advanced stellarator NCSX. Plasma Phys. Control. Fusion 43 (12A), A237.CrossRefGoogle Scholar
Zhu, C., Hudson, S. R., Song, Y. & Wan, Y. 2018 New method to design stellarator coils without the winding surface. Nucl. Fusion 58, 016008.CrossRefGoogle Scholar