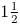1 Introduction
Structure-preserving particle-in-cell (PIC) algorithms preserve many of the geometric and topological mathematical structures of a point-particle kinetic plasma model, including its symplectic structure, symmetries, conservation laws and cohomology (Villasenor & Buneman Reference Villasenor and Buneman1992; Esirkepov Reference Esirkepov2001; Squire, Qin & Tang Reference Squire, Qin and Tang2012; Evstatiev & Shadwick Reference Evstatiev and Shadwick2013; Xiao et al. Reference Xiao, Liu, Qin and Yu2013; Crouseilles, Einkemmer & Faou Reference Crouseilles, Einkemmer and Faou2015; He et al. Reference He, Qin, Sun, Xiao, Zhang and Liu2015; Moon, Teixeira & Omelchenko Reference Moon, Teixeira and Omelchenko2015; Qin et al. Reference Qin, He, Zhang, Liu, Xiao and Wang2015, Reference Qin, Liu, Xiao, Zhang, He, Wang, Sun, Burby, Ellison and Zhou2016; Xiao et al. Reference Xiao, Qin, Liu, He, Zhang and Sun2015; He et al. Reference He, Sun, Qin and Liu2016; Burby Reference Burby2017; Kraus & Hirvijoki Reference Kraus and Hirvijoki2017; Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017; Morrison Reference Morrison2017; Xiao, Qin & Liu Reference Xiao, Qin and Liu2018; Xiao & Qin Reference Xiao and Qin2019; Glasser & Qin Reference Glasser and Qin2020; Hirvijoki, Kormann & Zonta Reference Hirvijoki, Kormann and Zonta2020; Holderied, Possanner & Wang Reference Holderied, Possanner and Wang2021; Kormann & Sonnendrücker Reference Kormann and Sonnendrücker2021; O'Connor et al. Reference O'Connor, Crawford, Ramachandran, Luginsland and Shanker2021; Perse, Kormann & Sonnendrücker Reference Perse, Kormann and Sonnendrücker2021; Pinto, Kormann & Sonnendrücker Reference Pinto, Kormann and Sonnendrücker2022; Wang et al. Reference Wang, Qin, Sturdevant and Chang2021; Xiao & Qin Reference Xiao and Qin2021). One such structure, gauge symmetry, was first preserved in a PIC algorithm in the Lagrangian formalism via a variational method (Squire et al. Reference Squire, Qin and Tang2012). More recently, it was also demonstrated that gauge symmetry could be exactly preserved in a Hamiltonian PIC algorithm via a gauge-compatible splitting method (Glasser & Qin Reference Glasser and Qin2020), or GCSM.
GCSMs are splitting methods whose sub-Hamiltonians ${H_i}$![]() (satisfying ${H=\sum H_i}$
(satisfying ${H=\sum H_i}$![]() ) are each gauge symmetric and exactly numerically integrable. It can be shown that such methods preserve the momentum map (Souriau Reference Souriau1970; Marsden & Ratiu Reference Marsden and Ratiu1999; da Silva Reference da Silva2001) of a gauge-symmetric Hamiltonian system. In a GCSM PIC algorithm, the momentum map $\mu$
) are each gauge symmetric and exactly numerically integrable. It can be shown that such methods preserve the momentum map (Souriau Reference Souriau1970; Marsden & Ratiu Reference Marsden and Ratiu1999; da Silva Reference da Silva2001) of a gauge-symmetric Hamiltonian system. In a GCSM PIC algorithm, the momentum map $\mu$![]() associated with electromagnetic gauge symmetry forms a discrete equivalent of Gauss’ law, characterized by the electric field ${ {\boldsymbol {E}}}$
associated with electromagnetic gauge symmetry forms a discrete equivalent of Gauss’ law, characterized by the electric field ${ {\boldsymbol {E}}}$![]() and charge density $\rho$
and charge density $\rho$![]() as ${\mu \sim (\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {E}}-4{\rm \pi} \rho )/4{\rm \pi} c}$
as ${\mu \sim (\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {E}}-4{\rm \pi} \rho )/4{\rm \pi} c}$![]() (in Gaussian units). Its preservation – ${\dot {\mu }=0}$
(in Gaussian units). Its preservation – ${\dot {\mu }=0}$![]() – enforces a discrete local charge conservation law throughout the simulation domain. As we shall see, specifying this momentum map $\mu$
– enforces a discrete local charge conservation law throughout the simulation domain. As we shall see, specifying this momentum map $\mu$![]() as an initial condition of a plasma simulation furthermore enables the precise assignment of any fixed background charge that may be desired throughout a simulation.
as an initial condition of a plasma simulation furthermore enables the precise assignment of any fixed background charge that may be desired throughout a simulation.
Most of the literature's recent structure-preserving Hamiltonian PIC methods employ a non-canonical Poisson structure to describe position and velocity particle degrees of freedom ${( {\boldsymbol {X}}, {\boldsymbol {V}})}$![]() and discrete electric and magnetic fields ${( {\boldsymbol {E}}, {\boldsymbol {B}})}$
and discrete electric and magnetic fields ${( {\boldsymbol {E}}, {\boldsymbol {B}})}$![]() (Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015; He et al. Reference He, Qin, Sun, Xiao, Zhang and Liu2015; Qin et al. Reference Qin, He, Zhang, Liu, Xiao and Wang2015; Xiao et al. Reference Xiao, Qin, Liu, He, Zhang and Sun2015; He et al. Reference He, Sun, Qin and Liu2016; Burby Reference Burby2017; Kraus & Hirvijoki Reference Kraus and Hirvijoki2017; Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017; Morrison Reference Morrison2017; Xiao et al. Reference Xiao, Qin and Liu2018; Xiao & Qin Reference Xiao and Qin2019, Reference Xiao and Qin2021; Holderied et al. Reference Holderied, Possanner and Wang2021; Kormann & Sonnendrücker Reference Kormann and Sonnendrücker2021; Perse et al. Reference Perse, Kormann and Sonnendrücker2021; Pinto et al. Reference Pinto, Kormann and Sonnendrücker2022). This approach hides from view the gauge symmetry of the Vlasov–Maxwell system and the simplicity of its canonical Poisson structure, characterized by the electromagnetic potential $ {\boldsymbol {A}}$
(Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015; He et al. Reference He, Qin, Sun, Xiao, Zhang and Liu2015; Qin et al. Reference Qin, He, Zhang, Liu, Xiao and Wang2015; Xiao et al. Reference Xiao, Qin, Liu, He, Zhang and Sun2015; He et al. Reference He, Sun, Qin and Liu2016; Burby Reference Burby2017; Kraus & Hirvijoki Reference Kraus and Hirvijoki2017; Kraus et al. Reference Kraus, Kormann, Morrison and Sonnendrücker2017; Morrison Reference Morrison2017; Xiao et al. Reference Xiao, Qin and Liu2018; Xiao & Qin Reference Xiao and Qin2019, Reference Xiao and Qin2021; Holderied et al. Reference Holderied, Possanner and Wang2021; Kormann & Sonnendrücker Reference Kormann and Sonnendrücker2021; Perse et al. Reference Perse, Kormann and Sonnendrücker2021; Pinto et al. Reference Pinto, Kormann and Sonnendrücker2022). This approach hides from view the gauge symmetry of the Vlasov–Maxwell system and the simplicity of its canonical Poisson structure, characterized by the electromagnetic potential $ {\boldsymbol {A}}$![]() and its conjugate momentum ${ {\boldsymbol {Y}}\sim \mathrm {d} {\boldsymbol {A}}/\mathrm {d} t}$
and its conjugate momentum ${ {\boldsymbol {Y}}\sim \mathrm {d} {\boldsymbol {A}}/\mathrm {d} t}$![]() , as well as particle position and momentum, ${( {\boldsymbol {X}}, {\boldsymbol {P}})}$
, as well as particle position and momentum, ${( {\boldsymbol {X}}, {\boldsymbol {P}})}$![]() . The process of ‘hiding’ this gauge symmetry may be formally regarded as the Poisson reduction of the Vlasov–Maxwell system (Marsden & Weinstein Reference Marsden and Weinstein1974, Reference Marsden and Weinstein1982; Marsden & Ratiu Reference Marsden and Ratiu1986; Glasser & Qin Reference Glasser and Qin2020), which strips out gauge symmetry to reduce canonical coordinates ${( {\boldsymbol {A}}, {\boldsymbol {Y}}, {\boldsymbol {X}}, {\boldsymbol {P}})}$
. The process of ‘hiding’ this gauge symmetry may be formally regarded as the Poisson reduction of the Vlasov–Maxwell system (Marsden & Weinstein Reference Marsden and Weinstein1974, Reference Marsden and Weinstein1982; Marsden & Ratiu Reference Marsden and Ratiu1986; Glasser & Qin Reference Glasser and Qin2020), which strips out gauge symmetry to reduce canonical coordinates ${( {\boldsymbol {A}}, {\boldsymbol {Y}}, {\boldsymbol {X}}, {\boldsymbol {P}})}$![]() to their non-canonical counterparts ${( {\boldsymbol {E}}, {\boldsymbol {B}}, {\boldsymbol {X}}, {\boldsymbol {V}})}$
to their non-canonical counterparts ${( {\boldsymbol {E}}, {\boldsymbol {B}}, {\boldsymbol {X}}, {\boldsymbol {V}})}$![]() .
.
In this work, we demonstrate the effectiveness of the canonical formalism in simulating the Vlasov–Maxwell system. Using the flexible techniques of finite element exterior calculus (Arnold, Falk & Winther Reference Arnold, Falk and Winther2006, Reference Arnold, Falk and Winther2010) previously adopted in Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017), we discover a canonical finite element Poisson structure for the Vlasov–Maxwell system. From this discrete structure, we derive a gauge-compatible splitting method that defines an exactly solvable symplectic PIC algorithm. We characterize the gauge symmetry of this algorithm and use it to derive the charge-conserving momentum map, $\mu$![]() . We further demonstrate the use of $\mu$
. We further demonstrate the use of $\mu$![]() to establish initial conditions with a simple numerical example of a fixed, homogeneous, neutralizing, positive background charge in a Landau damping simulation. Lastly, we consider the restriction of our method to a $1\frac {1}{2}$
to establish initial conditions with a simple numerical example of a fixed, homogeneous, neutralizing, positive background charge in a Landau damping simulation. Lastly, we consider the restriction of our method to a $1\frac {1}{2}$![]() -dimensional (Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015) 1X2P phase space. We demonstrate that this subsystem retains the essential gauge structure of the Vlasov–Maxwell system, and test its numerical efficacy with a simulation of the Weibel instability (Weibel Reference Weibel1959).
-dimensional (Crouseilles et al. Reference Crouseilles, Einkemmer and Faou2015) 1X2P phase space. We demonstrate that this subsystem retains the essential gauge structure of the Vlasov–Maxwell system, and test its numerical efficacy with a simulation of the Weibel instability (Weibel Reference Weibel1959).
The remainder of this article is organized as follows. In § 2, we briefly introduce the momentum map. In § 3, we describe aspects of finite element exterior calculus that are used in the algorithm. In § 4, we derive the canonical Poisson structure of the discrete Vlasov–Maxwell system, its Hamiltonian and its momentum map. In § 5, a GCSM is derived. In § 6, we describe the practical use of the momentum map, and present numerical results from Landau damping and Weibel instability simulations. In § 7, we summarize and conclude.
2 A brief review of the momentum map
The momentum map (Souriau Reference Souriau1970; Marsden & Ratiu Reference Marsden and Ratiu1999; da Silva Reference da Silva2001) may be viewed as the Hamiltonian manifestation of the Noether principle – i.e. that every smooth symmetry of a dynamical system corresponds to a conserved quantity. We may demonstrate how the momentum map arises from the symmetry transformations of a Lie group on a Poisson manifold, as follows.
Suppose a Poisson manifold $M$![]() is equipped with symmetry transformations defined by the group action ${\varPhi :G\times M\rightarrow M}$
is equipped with symmetry transformations defined by the group action ${\varPhi :G\times M\rightarrow M}$![]() , where $G$
, where $G$![]() is a Lie group whose elements act upon $M$
is a Lie group whose elements act upon $M$![]() . The group action $\varPhi _g$
. The group action $\varPhi _g$![]() associated with any fixed ${g\in G}$
associated with any fixed ${g\in G}$![]() is defined such that $\varPhi _g(x)=\varPhi (g,x)\ \forall \ {x\in M}$
is defined such that $\varPhi _g(x)=\varPhi (g,x)\ \forall \ {x\in M}$![]() . The corresponding Lie algebra ${\mathfrak {g}=\text {Lie}(G)}$
. The corresponding Lie algebra ${\mathfrak {g}=\text {Lie}(G)}$![]() , may be regarded as generating these symmetry transformations, since $\forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$
, may be regarded as generating these symmetry transformations, since $\forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$![]() there exists a vector field ${X_{ {\boldsymbol {s}}}\in \mathfrak {X}(M)}$
there exists a vector field ${X_{ {\boldsymbol {s}}}\in \mathfrak {X}(M)}$![]() on $M$
on $M$![]() defined by
defined by
Here, ${\{\exp (\epsilon {\boldsymbol {s}})\in G~|~\epsilon \in \mathbb {R}\}}$![]() is the one-parameter subgroup of $G$
is the one-parameter subgroup of $G$![]() generated by $ {\boldsymbol {s}}$
generated by $ {\boldsymbol {s}}$![]() . Thus, the vector field $X_{ {\boldsymbol {s}}}$
. Thus, the vector field $X_{ {\boldsymbol {s}}}$![]() is seen to ‘infinitesimally generate’ the family of symmetry transformations ${\varPhi _{\exp (\epsilon {\boldsymbol {s}})}}$
is seen to ‘infinitesimally generate’ the family of symmetry transformations ${\varPhi _{\exp (\epsilon {\boldsymbol {s}})}}$![]() . Equivalently, one may regard the collection of maps ${\{\varPhi _{\exp (\epsilon {\boldsymbol {s}})}:M\rightarrow M~|~\epsilon \in \mathbb {R}\}}$
. Equivalently, one may regard the collection of maps ${\{\varPhi _{\exp (\epsilon {\boldsymbol {s}})}:M\rightarrow M~|~\epsilon \in \mathbb {R}\}}$![]() as the flow of $M$
as the flow of $M$![]() along the vector field $X_{ {\boldsymbol {s}}}$
along the vector field $X_{ {\boldsymbol {s}}}$![]() . In this way, each Lie algebra generator ${ {\boldsymbol {s}}\in \mathfrak {g}}$
. In this way, each Lie algebra generator ${ {\boldsymbol {s}}\in \mathfrak {g}}$![]() corresponds to a generator of transformations on $M$
corresponds to a generator of transformations on $M$![]() – namely, the vector field $X_{ {\boldsymbol {s}}}$
– namely, the vector field $X_{ {\boldsymbol {s}}}$![]() .
.
Now suppose ${\{\cdot,\cdot \}:C^{\infty }(M)\times C^{\infty }(M)\rightarrow C^{\infty }(M)}$![]() denotes the Poisson bracket on $M$
denotes the Poisson bracket on $M$![]() , defining an algebra of smooth functions. The momentum map is then defined as a linear map ${\mu :\mathfrak {g}\rightarrow C^{\infty }(M)}$
, defining an algebra of smooth functions. The momentum map is then defined as a linear map ${\mu :\mathfrak {g}\rightarrow C^{\infty }(M)}$![]() which assigns to every $ {\boldsymbol {s}}\in \mathfrak {g}$
which assigns to every $ {\boldsymbol {s}}\in \mathfrak {g}$![]() a generating function ${\mu ( {\boldsymbol {s}})\in C^{\infty }(M)}$
a generating function ${\mu ( {\boldsymbol {s}})\in C^{\infty }(M)}$![]() – henceforth denoted ${\mu _{ {\boldsymbol {s}}}=\mu ( {\boldsymbol {s}})}$
– henceforth denoted ${\mu _{ {\boldsymbol {s}}}=\mu ( {\boldsymbol {s}})}$![]() – satisfying
– satisfying
Here, ${X_{ {\boldsymbol {s}}}(F)}$![]() denotes the Lie derivative of $F$
denotes the Lie derivative of $F$![]() by the vector field $X_{ {\boldsymbol {s}}}$
by the vector field $X_{ {\boldsymbol {s}}}$![]() . In this way, $\mu _{ {\boldsymbol {s}}}$
. In this way, $\mu _{ {\boldsymbol {s}}}$![]() is a generating function via the Poisson bracket for the symmetry transformation generated by $ {\boldsymbol {s}}$
is a generating function via the Poisson bracket for the symmetry transformation generated by $ {\boldsymbol {s}}$![]() ; in particular, ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$
; in particular, ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$![]() are equal as derivations on $C^\infty(M)$
are equal as derivations on $C^\infty(M)$![]() . Therefore, when a momentum map $\mu$
. Therefore, when a momentum map $\mu$![]() is defined, each ${ {\boldsymbol {s}}\in \mathfrak {g}}$
is defined, each ${ {\boldsymbol {s}}\in \mathfrak {g}}$![]() corresponds not only to a vector field $X_{ {\boldsymbol {s}}}$
corresponds not only to a vector field $X_{ {\boldsymbol {s}}}$![]() on $M$
on $M$![]() , but to a generating function ${\mu _{ {\boldsymbol {s}}}\in C^{\infty }(M)}$
, but to a generating function ${\mu _{ {\boldsymbol {s}}}\in C^{\infty }(M)}$![]() as well. The linearity of $\mu$
as well. The linearity of $\mu$![]() implies that ${\mu _{ {\boldsymbol {s}}+ {\boldsymbol {t}}}=\mu _{ {\boldsymbol {s}}}+\mu _{ {\boldsymbol {t}}}}$
implies that ${\mu _{ {\boldsymbol {s}}+ {\boldsymbol {t}}}=\mu _{ {\boldsymbol {s}}}+\mu _{ {\boldsymbol {t}}}}$![]() , and we more generally denote $\mu$
, and we more generally denote $\mu$![]() as the map satisfying ${\mu \boldsymbol{\cdot} {\boldsymbol {s}}=\mu _{ {\boldsymbol {s}}}}\ \forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$
as the map satisfying ${\mu \boldsymbol{\cdot} {\boldsymbol {s}}=\mu _{ {\boldsymbol {s}}}}\ \forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$![]() .
.
In a symmetric Hamiltonian system, the function $\mu _{ {\boldsymbol {s}}}$![]() is not only a generator of a symmetry transformation, but also a conserved quantity. To see this, consider a symmetric Hamiltonian ${H\in C^{\infty }(M)}$
is not only a generator of a symmetry transformation, but also a conserved quantity. To see this, consider a symmetric Hamiltonian ${H\in C^{\infty }(M)}$![]() that is invariant under a group action $\varPhi$
that is invariant under a group action $\varPhi$![]() , such that
, such that
Setting ${g=\exp (\epsilon {\boldsymbol {s}})}$![]() and differentiating both sides of (2.3) with respect to $\epsilon$
and differentiating both sides of (2.3) with respect to $\epsilon$![]() , it follows by (2.1) that ${X_{ {\boldsymbol {s}}}(H)=0}$
, it follows by (2.1) that ${X_{ {\boldsymbol {s}}}(H)=0}$![]() $\forall$
$\forall$![]() ${ {\boldsymbol {s}}\in \mathfrak {g}}$
${ {\boldsymbol {s}}\in \mathfrak {g}}$![]() . By (2.2), then,
. By (2.2), then,
Therefore, $\mu _{ {\boldsymbol {s}}}$![]() is constant along the flow generated by $H$
is constant along the flow generated by $H$![]() on $M$
on $M$![]() , i.e. it is conserved in time. Since ${0=\dot {\mu }^{ {\boldsymbol {s}}}=\mathrm {d}/\mathrm {d} t(\mu \boldsymbol {\cdot } {\boldsymbol {s}})=\dot {\mu }\boldsymbol {\cdot } {\boldsymbol {s}}}\ \forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$
, i.e. it is conserved in time. Since ${0=\dot {\mu }^{ {\boldsymbol {s}}}=\mathrm {d}/\mathrm {d} t(\mu \boldsymbol {\cdot } {\boldsymbol {s}})=\dot {\mu }\boldsymbol {\cdot } {\boldsymbol {s}}}\ \forall \ { {\boldsymbol {s}}\in \mathfrak {g}}$![]() , we more generally write that ${\dot {\mu }=0}$
, we more generally write that ${\dot {\mu }=0}$![]() .
.
3 Relevant aspects of finite element exterior calculus
We now introduce notation and briefly describe elementary aspects of finite element exterior calculus (Arnold et al. Reference Arnold, Falk and Winther2006, Reference Arnold, Falk and Winther2010), abbreviated FEEC. To approximate differential forms on a smooth manifold $\varOmega$![]() by finite elements, FEEC projects the de Rham complex of differential forms ${0\xrightarrow {\mathrm {d}}\varLambda ^{0}(\varOmega )\xrightarrow {\mathrm {d}}\cdots \xrightarrow {\mathrm {d}}\varLambda ^{n}(\varOmega )\xrightarrow {\mathrm {d}}0}$
by finite elements, FEEC projects the de Rham complex of differential forms ${0\xrightarrow {\mathrm {d}}\varLambda ^{0}(\varOmega )\xrightarrow {\mathrm {d}}\cdots \xrightarrow {\mathrm {d}}\varLambda ^{n}(\varOmega )\xrightarrow {\mathrm {d}}0}$![]() onto spaces of piecewise polynomial differential forms, as depicted in figure 1. In particular, given a triangulation of $\varOmega$
onto spaces of piecewise polynomial differential forms, as depicted in figure 1. In particular, given a triangulation of $\varOmega$![]() denoted $\mathcal {T}_h$
denoted $\mathcal {T}_h$![]() (with maximum diameter $h$
(with maximum diameter $h$![]() on any given cell), ${\varLambda ^{p}(\mathcal {T}_h)}$
on any given cell), ${\varLambda ^{p}(\mathcal {T}_h)}$![]() denotes some finite-dimensional space of piecewise $p$
denotes some finite-dimensional space of piecewise $p$![]() -forms on $\mathcal {T}_h$
-forms on $\mathcal {T}_h$![]() whose coefficients are polynomial over each $p$
whose coefficients are polynomial over each $p$![]() -cell of $\mathcal {T}_h$
-cell of $\mathcal {T}_h$![]() . The projection map ${{\rm \pi} _h:\varLambda ^{p}(\varOmega )\rightarrow \varLambda ^{p}(\mathcal {T}_h)}$
. The projection map ${{\rm \pi} _h:\varLambda ^{p}(\varOmega )\rightarrow \varLambda ^{p}(\mathcal {T}_h)}$![]() for each $p$
for each $p$![]() is required to ensure that the diagram of figure 1 commutes – in particular, that ${{\rm \pi} _h\circ \mathrm {d}=\mathrm {d}\circ {\rm \pi}_h}$
is required to ensure that the diagram of figure 1 commutes – in particular, that ${{\rm \pi} _h\circ \mathrm {d}=\mathrm {d}\circ {\rm \pi}_h}$![]() . The horizontal arrows of figure 1 are required to form cochain complexes ($\mathrm {d}\circ \mathrm {d}=0$
. The horizontal arrows of figure 1 are required to form cochain complexes ($\mathrm {d}\circ \mathrm {d}=0$![]() ) such that the projections ${\rm \pi} _h$
) such that the projections ${\rm \pi} _h$![]() are isomorphisms of cohomology. There exist many possible choices for the finite element spaces ${\varLambda ^{p}(\mathcal {T}_h)}$
are isomorphisms of cohomology. There exist many possible choices for the finite element spaces ${\varLambda ^{p}(\mathcal {T}_h)}$![]() , which can vary in their degree of accuracy and with the choice of triangulation $\mathcal {T}_h$
, which can vary in their degree of accuracy and with the choice of triangulation $\mathcal {T}_h$![]() . However, any such choice must ensure that the sequence of spaces ${\cdots \rightarrow \varLambda ^{p}(\mathcal {T}_h)\rightarrow \cdots }$
. However, any such choice must ensure that the sequence of spaces ${\cdots \rightarrow \varLambda ^{p}(\mathcal {T}_h)\rightarrow \cdots }$![]() constitutes a cochain complex, and that the finite element problem being studied is solvable and well posed in those spaces.
constitutes a cochain complex, and that the finite element problem being studied is solvable and well posed in those spaces.

Figure 1. Given a triangulation $\mathcal {T}_h$![]() of the smooth manifold $\varOmega$
of the smooth manifold $\varOmega$![]() , each space of differential forms ${\varLambda ^{p}(\varOmega )}$
, each space of differential forms ${\varLambda ^{p}(\varOmega )}$![]() of the continuous cochain complex is projected onto a finite element space ${\varLambda ^{p}(\mathcal {T}_h)}$
of the continuous cochain complex is projected onto a finite element space ${\varLambda ^{p}(\mathcal {T}_h)}$![]() . There are many possible choices, of varying degrees of accuracy, for the spaces of piecewise polynomial finite elements ${\varLambda ^{p}(\mathcal {T}_h)}$
. There are many possible choices, of varying degrees of accuracy, for the spaces of piecewise polynomial finite elements ${\varLambda ^{p}(\mathcal {T}_h)}$![]() . The projections ${\rm \pi} _h$
. The projections ${\rm \pi} _h$![]() are required to satisfy ${{\rm \pi} _h\circ \mathrm {d}=\mathrm {d}\circ {\rm \pi}_h}$
are required to satisfy ${{\rm \pi} _h\circ \mathrm {d}=\mathrm {d}\circ {\rm \pi}_h}$![]() , such that the diagram above is commuting.
, such that the diagram above is commuting.
For example, a straightforward choice for ${\varLambda ^{p}(\mathcal {T}_h)}$![]() is given by the space of all piecewise polynomial $p$
is given by the space of all piecewise polynomial $p$![]() -forms of degree ${\leqslant }r$
-forms of degree ${\leqslant }r$![]() , denoted ${\mathcal {P}_r\varLambda ^{p}(\mathcal {T}_h)}$
, denoted ${\mathcal {P}_r\varLambda ^{p}(\mathcal {T}_h)}$![]() . An alternative, more lightweight choice for ${\varLambda ^{p}(\mathcal {T}_h)}$
. An alternative, more lightweight choice for ${\varLambda ^{p}(\mathcal {T}_h)}$![]() is the space of Whitney $p$
is the space of Whitney $p$![]() -forms (Whitney Reference Whitney1957). These are piecewise linear forms that can be defined using barycentric coordinate functions ${\{\lambda _0,\dots,\lambda _p\}}$
-forms (Whitney Reference Whitney1957). These are piecewise linear forms that can be defined using barycentric coordinate functions ${\{\lambda _0,\dots,\lambda _p\}}$![]() such that, for any $p$
such that, for any $p$![]() -simplex $\sigma$
-simplex $\sigma$![]() , the Whitney $p$
, the Whitney $p$![]() -form $\phi _\sigma$
-form $\phi _\sigma$![]() associated with $\sigma$
associated with $\sigma$![]() is given by
is given by

(Here, the hat signifies that ${\mathrm {d}\lambda _{\sigma (i)}}$![]() is omitted.) We refer the reader to Arnold et al. (Reference Arnold, Falk and Winther2006, Reference Arnold, Falk and Winther2010), Arnold & Awanou (Reference Arnold and Awanou2013) and Arnold, Boffi & Bonizzoni (Reference Arnold, Boffi and Bonizzoni2015) for more detailed descriptions of cochain-complex-conforming finite element spaces.
is omitted.) We refer the reader to Arnold et al. (Reference Arnold, Falk and Winther2006, Reference Arnold, Falk and Winther2010), Arnold & Awanou (Reference Arnold and Awanou2013) and Arnold, Boffi & Bonizzoni (Reference Arnold, Boffi and Bonizzoni2015) for more detailed descriptions of cochain-complex-conforming finite element spaces.
We may fix a notation for calculations with finite elements independent of the choice of space $\varLambda ^{p}(\mathcal {T}_h)$![]() . For any such choice, we may fix a basis for ${\varLambda ^{p}(\mathcal {T}_h)}$
. For any such choice, we may fix a basis for ${\varLambda ^{p}(\mathcal {T}_h)}$![]() with $N_p$
with $N_p$![]() finite elements, and organize them into the ${N_p\times 1}$
finite elements, and organize them into the ${N_p\times 1}$![]() vector ${ { \boldsymbol {\varLambda }}^{p}}$
vector ${ { \boldsymbol {\varLambda }}^{p}}$![]() . The $i\text {th}$
. The $i\text {th}$![]() entry of ${ { \boldsymbol {\varLambda }}^{p}}$
entry of ${ { \boldsymbol {\varLambda }}^{p}}$![]() is a basis element we denote ${\varLambda ^{p}_i\in \varLambda ^{p}(\mathcal {T}_h)}$
is a basis element we denote ${\varLambda ^{p}_i\in \varLambda ^{p}(\mathcal {T}_h)}$![]() , which defines a piecewise polynomial $p$
, which defines a piecewise polynomial $p$![]() -form on $\mathcal {T}_h$
-form on $\mathcal {T}_h$![]() . Any $p$
. Any $p$![]() -form ${ {\boldsymbol {S}}\in \varLambda ^{p}(\mathcal {T}_h)}$
-form ${ {\boldsymbol {S}}\in \varLambda ^{p}(\mathcal {T}_h)}$![]() may thus be expanded in the $ { \boldsymbol {\varLambda }}^{p}$
may thus be expanded in the $ { \boldsymbol {\varLambda }}^{p}$![]() basis as
basis as
$\forall$![]() ${ {\boldsymbol {x}}\in \left | {\mathcal {T}_h} \right |}$
${ {\boldsymbol {x}}\in \left | {\mathcal {T}_h} \right |}$![]() (where ${\left | {\mathcal {T}_h} \right |\subset \mathbb {R}^{n}}$
(where ${\left | {\mathcal {T}_h} \right |\subset \mathbb {R}^{n}}$![]() denotes the convex hull of $\mathcal {T}_h$
denotes the convex hull of $\mathcal {T}_h$![]() ). The individual components of $ {\boldsymbol {S}}$
). The individual components of $ {\boldsymbol {S}}$![]() will be denoted
will be denoted
Here, ${ {\boldsymbol {s}}\in \mathbb {R}^{N_p}}$![]() and Einstein summation convention is used for the repeated $i$
and Einstein summation convention is used for the repeated $i$![]() index. Greek letters denote coordinate indices. For ${\left | {\mathcal {T}_h} \right |\subset \mathbb {R}^{3}}$
index. Greek letters denote coordinate indices. For ${\left | {\mathcal {T}_h} \right |\subset \mathbb {R}^{3}}$![]() , for example, the $\mu \text {th}$
, for example, the $\mu \text {th}$![]() component of the 1-form basis element $\varLambda ^{1}_i( {\boldsymbol {x}})$
component of the 1-form basis element $\varLambda ^{1}_i( {\boldsymbol {x}})$![]() is denoted ${\varLambda ^{1}_i( {\boldsymbol {x}})_\mu }\ \forall \ {\mu \in \{1,2,3\}}$
is denoted ${\varLambda ^{1}_i( {\boldsymbol {x}})_\mu }\ \forall \ {\mu \in \{1,2,3\}}$![]() , such that ${\varLambda ^{1}_i( {\boldsymbol {x}})=\varLambda ^{1}_i( {\boldsymbol {x}})_\mu \,\mathrm {d} x^{\mu }}$
, such that ${\varLambda ^{1}_i( {\boldsymbol {x}})=\varLambda ^{1}_i( {\boldsymbol {x}})_\mu \,\mathrm {d} x^{\mu }}$![]() .
.
Exterior calculus may be computed in the ${ { \boldsymbol {\varLambda }}^{0},\dots, { \boldsymbol {\varLambda }}^{n}}$![]() bases by simple matrix multiplication. Let us define this explicitly on $\mathbb {R}^{3}$
bases by simple matrix multiplication. Let us define this explicitly on $\mathbb {R}^{3}$![]() , where the exterior derivatives of $\text {0-, 1-}$
, where the exterior derivatives of $\text {0-, 1-}$![]() and ${\text {2-forms}}$
and ${\text {2-forms}}$![]() can be implemented via matrices that represent the gradient ($\mathbb {G}$
can be implemented via matrices that represent the gradient ($\mathbb {G}$![]() ), curl ($\mathbb {C}$
), curl ($\mathbb {C}$![]() ) and divergence ($\mathbb {D}$
) and divergence ($\mathbb {D}$![]() ), respectively. In table 1, we define these matrices to act on the coefficients of forms so as to compute the forms’ exterior derivatives. For example, the gradient of the 0-form ${ {\boldsymbol {S}}= {\boldsymbol {s}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{0}}$
), respectively. In table 1, we define these matrices to act on the coefficients of forms so as to compute the forms’ exterior derivatives. For example, the gradient of the 0-form ${ {\boldsymbol {S}}= {\boldsymbol {s}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{0}}$![]() is computed to be ${\mathrm {d} {\boldsymbol {S}}=\mathbb {G} {\boldsymbol {s}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$
is computed to be ${\mathrm {d} {\boldsymbol {S}}=\mathbb {G} {\boldsymbol {s}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() , where the matrix ${\mathbb {G}\in \mathbb {R}^{N_1\times N_0}}$
, where the matrix ${\mathbb {G}\in \mathbb {R}^{N_1\times N_0}}$![]() is defined such that ${\mathrm {d} { \boldsymbol {\varLambda }}^{0}=\mathbb {G}^{T} { \boldsymbol {\varLambda }}^{1}}$
is defined such that ${\mathrm {d} { \boldsymbol {\varLambda }}^{0}=\mathbb {G}^{T} { \boldsymbol {\varLambda }}^{1}}$![]() . This definition gives the desired result since
. This definition gives the desired result since
Table 1. The finite element matrix implementation of $\mathrm {d}$![]() on $\mathbb {R}^{3}$
on $\mathbb {R}^{3}$![]() . The property ${\mathrm {d}\circ \mathrm {d}=0}$
. The property ${\mathrm {d}\circ \mathrm {d}=0}$![]() implies that ${\mathbb {C}\mathbb {G}=0}$
implies that ${\mathbb {C}\mathbb {G}=0}$![]() and ${\mathbb {D}\mathbb {C}=0}$
and ${\mathbb {D}\mathbb {C}=0}$![]() .
.

Lastly, it will be useful to define the mass matrix on $\mathcal {T}_h$![]() for each basis $ { \boldsymbol {\varLambda }}^{p}$
for each basis $ { \boldsymbol {\varLambda }}^{p}$![]() of finite element $p$
of finite element $p$![]() -forms. Specifically, we define the mass matrix ${\mathbb {M}_p\in \mathbb {R}^{N_p\times N_p}}$
-forms. Specifically, we define the mass matrix ${\mathbb {M}_p\in \mathbb {R}^{N_p\times N_p}}$![]() of $ { \boldsymbol {\varLambda }}^{p}$
of $ { \boldsymbol {\varLambda }}^{p}$![]() by
by
Here, ${(\cdot,\cdot )_p}$![]() denotes the inner product on $p$
denotes the inner product on $p$![]() -forms induced by the metric $g_{\mu \nu }$
-forms induced by the metric $g_{\mu \nu }$![]() , namely
, namely

On $\mathbb {R}^{3}$![]() , for example, (3.6) defines ${(\alpha,\beta )_p}$
, for example, (3.6) defines ${(\alpha,\beta )_p}$![]() for ${p=1,2}$
for ${p=1,2}$![]() simply as the standard inner product ${\alpha \boldsymbol{\cdot} \beta }$
simply as the standard inner product ${\alpha \boldsymbol{\cdot} \beta }$![]() . After all, 1- and 2-forms each have three independent components on $\mathbb {R}^{3}$
. After all, 1- and 2-forms each have three independent components on $\mathbb {R}^{3}$![]() and ${g_{\mu \nu }=\delta _{\mu \nu }}$
and ${g_{\mu \nu }=\delta _{\mu \nu }}$![]() . We note that ${(\alpha,\beta )_p}$
. We note that ${(\alpha,\beta )_p}$![]() is symmetric, such that ${\mathbb {M}_p^{T}=\mathbb {M}_p}$
is symmetric, such that ${\mathbb {M}_p^{T}=\mathbb {M}_p}$![]() . Equation (3.5) may be understood to define the Hodge star operator $\star$
. Equation (3.5) may be understood to define the Hodge star operator $\star$![]() , such that ${\alpha \wedge \star \beta =(\alpha,\beta )_p\,\mathrm {d} {\boldsymbol {x}}}$
, such that ${\alpha \wedge \star \beta =(\alpha,\beta )_p\,\mathrm {d} {\boldsymbol {x}}}$![]() for arbitrary $p$
for arbitrary $p$![]() -forms $\alpha$
-forms $\alpha$![]() and $\beta$
and $\beta$![]() , where $\mathrm {d} {\boldsymbol {x}}$
, where $\mathrm {d} {\boldsymbol {x}}$![]() denotes the unique volume form that evaluates to unity on positively oriented vectors that are orthonormal with respect to $g_{\mu \nu }$
denotes the unique volume form that evaluates to unity on positively oriented vectors that are orthonormal with respect to $g_{\mu \nu }$![]() . The mass matrix will evidently appear wherever metric information is incorporated via the Hodge star.
. The mass matrix will evidently appear wherever metric information is incorporated via the Hodge star.
4 A discrete Vlasov–Maxwell Poisson structure and Hamiltonian
We now apply the formalism above to define a canonical finite element Poisson structure and Hamiltonian for the Vlasov–Maxwell system. We first describe the Poisson structure of discrete electromagnetic fields on a triangulation $\mathcal {T}_h$![]() of the spatial manifold ${\varOmega \subset \mathbb {R}^{3}}$
of the spatial manifold ${\varOmega \subset \mathbb {R}^{3}}$![]() .
.
4.1 The finite element electromagnetic Poisson structure
To start, let us consider electromagnetic fields on the continuous manifold $\varOmega$![]() , using the temporal gauge wherein the electric potential vanishes, ${\phi =0}$
, using the temporal gauge wherein the electric potential vanishes, ${\phi =0}$![]() . The configuration space for such fields is the set ${Q=\{ {\boldsymbol {A}}~|~ {\boldsymbol {A}}\in \varLambda ^{1}(\varOmega )\}}$
. The configuration space for such fields is the set ${Q=\{ {\boldsymbol {A}}~|~ {\boldsymbol {A}}\in \varLambda ^{1}(\varOmega )\}}$![]() of possible vector potentials, defined as differential ${\text {1-forms}}$
of possible vector potentials, defined as differential ${\text {1-forms}}$![]() over $\varOmega$
over $\varOmega$![]() . To find a variable conjugate to $ {\boldsymbol {A}}( {\boldsymbol {x}})$
. To find a variable conjugate to $ {\boldsymbol {A}}( {\boldsymbol {x}})$![]() , we compute the following variational derivative of the electromagnetic Lagrangian expressed in Gaussian units,
, we compute the following variational derivative of the electromagnetic Lagrangian expressed in Gaussian units,

Clearly, ${ {\boldsymbol {Y}}\in \varLambda ^{1}(\varOmega )}$![]() is also a ${\text {1-form}}$
is also a ${\text {1-form}}$![]() over $\varOmega$
over $\varOmega$![]() corresponding to negative the electric field, ${ {\boldsymbol {Y}}=- {\boldsymbol {E}}/4{\rm \pi} c}$
corresponding to negative the electric field, ${ {\boldsymbol {Y}}=- {\boldsymbol {E}}/4{\rm \pi} c}$![]() . As in (3.6), ${\left | {\alpha } \right |^{2}=(\alpha,\alpha )_p}$
. As in (3.6), ${\left | {\alpha } \right |^{2}=(\alpha,\alpha )_p}$![]() in (4.1a) denotes the standard inner product on $\mathbb {R}^{3}$
in (4.1a) denotes the standard inner product on $\mathbb {R}^{3}$![]() for ${p=1,2}$
for ${p=1,2}$![]() .
.
The full phase space is then given by the cotangent bundle ${T^{*}Q=\{ {\boldsymbol {A}}, {\boldsymbol {Y}}\}}$![]() whose canonical symplectic structure is defined by the Poisson bracket (Marsden & Weinstein Reference Marsden and Weinstein1982)
whose canonical symplectic structure is defined by the Poisson bracket (Marsden & Weinstein Reference Marsden and Weinstein1982)
Here, ${F[ {\boldsymbol {A}}, {\boldsymbol {Y}}]}$![]() and ${G[ {\boldsymbol {A}}, {\boldsymbol {Y}}]}$
and ${G[ {\boldsymbol {A}}, {\boldsymbol {Y}}]}$![]() are arbitrary functionals on ${T^{*}Q}$
are arbitrary functionals on ${T^{*}Q}$![]() .
.
We now map this geometric description of fields on $\varOmega$![]() to its triangulation $\mathcal {T}_h$
to its triangulation $\mathcal {T}_h$![]() . On $\mathcal {T}_h$
. On $\mathcal {T}_h$![]() , the fields $ {\boldsymbol {A}}$
, the fields $ {\boldsymbol {A}}$![]() and $ {\boldsymbol {Y}}$
and $ {\boldsymbol {Y}}$![]() can be defined by their expansion in the corresponding basis for finite element ${\text {1-forms}}$
can be defined by their expansion in the corresponding basis for finite element ${\text {1-forms}}$![]()

Here, ${ { \boldsymbol {\varLambda }}^{1}}$![]() is an ${N_1\times 1}$
is an ${N_1\times 1}$![]() vector of basis elements and ${ {\boldsymbol {a}}, {\boldsymbol {y}}\in \mathbb {R}^{N_1}}$
vector of basis elements and ${ {\boldsymbol {a}}, {\boldsymbol {y}}\in \mathbb {R}^{N_1}}$![]() denote coefficients, as in (3.2). $ {\boldsymbol {a}}$
denote coefficients, as in (3.2). $ {\boldsymbol {a}}$![]() and $ {\boldsymbol {y}}$
and $ {\boldsymbol {y}}$![]() are identified as dynamical variables by explicitly notating their time dependence. The inverse factor of the 1-form mass matrix $\mathbb {M}_1$
are identified as dynamical variables by explicitly notating their time dependence. The inverse factor of the 1-form mass matrix $\mathbb {M}_1$![]() in (4.3) follows from computing the conjugate momentum of $ {\boldsymbol {a}}$
in (4.3) follows from computing the conjugate momentum of $ {\boldsymbol {a}}$![]() in the following discretization of $L_\textrm {EM}$
in the following discretization of $L_\textrm {EM}$![]() :
:

where we have substituted ${\mathrm {d} { \boldsymbol {\varLambda }}^{1}=\mathbb {C}^{T} { \boldsymbol {\varLambda }}^{2}}$![]() from table 1 and used mass matrices as defined in (3.5). Comparing (4.1a,b) and (4.4) yields the desired expansion for $ {\boldsymbol {Y}}$
from table 1 and used mass matrices as defined in (3.5). Comparing (4.1a,b) and (4.4) yields the desired expansion for $ {\boldsymbol {Y}}$![]() in (4.3). (This inverse factor of $\mathbb {M}_1$
in (4.3). (This inverse factor of $\mathbb {M}_1$![]() will further ensure that the Poisson bracket of (4.9) is canonical.)
will further ensure that the Poisson bracket of (4.9) is canonical.)
To discretize the Poisson bracket of (4.2), we must first express ${\delta F/\delta {\boldsymbol {A}}}$![]() in terms of ${\partial F/\partial {\boldsymbol {a}}}$
in terms of ${\partial F/\partial {\boldsymbol {a}}}$![]() for a discrete variation ${\delta {\boldsymbol {A}}=\delta {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$
for a discrete variation ${\delta {\boldsymbol {A}}=\delta {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() . Since variational derivatives are valued dually to their variations, following Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017), it is appropriate to require that
. Since variational derivatives are valued dually to their variations, following Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017), it is appropriate to require that
Here, ${\langle \cdot,\cdot \rangle _{L^{2}\varLambda ^{1}}=\int _{\left | {\mathcal {T}_h} \right |}\mathrm {d} {\boldsymbol {x}}(\cdot,\cdot )_{p=1}}$![]() denotes the ${L^{2}\varLambda ^{1}}$
denotes the ${L^{2}\varLambda ^{1}}$![]() inner product, and ${\langle \cdot,\cdot \rangle _{\mathbb {R}^{N_1}}}$
inner product, and ${\langle \cdot,\cdot \rangle _{\mathbb {R}^{N_1}}}$![]() the standard inner product on $\mathbb {R}^{N_1}$
the standard inner product on $\mathbb {R}^{N_1}$![]() . In particular, setting $\delta a_j=\delta _{ij}$
. In particular, setting $\delta a_j=\delta _{ij}$![]() for some fixed, arbitrary ${i\in [1,N_1]}$
for some fixed, arbitrary ${i\in [1,N_1]}$![]() and using ${(\cdot,\cdot )_p}$
and using ${(\cdot,\cdot )_p}$![]() as defined in (3.6), (4.5) yields
as defined in (3.6), (4.5) yields
To solve for ${\delta F/\delta {\boldsymbol {A}}}$![]() , we expand ${\delta F/\delta {\boldsymbol {A}}= {\boldsymbol {f}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$
, we expand ${\delta F/\delta {\boldsymbol {A}}= {\boldsymbol {f}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() in the ${ { \boldsymbol {\varLambda }}^{1}}$
in the ${ { \boldsymbol {\varLambda }}^{1}}$![]() basis for some ${ {\boldsymbol {f}}\in \mathbb {R}^{N_1}}$
basis for some ${ {\boldsymbol {f}}\in \mathbb {R}^{N_1}}$![]() , such that evaluating (4.6) implies ${ {\boldsymbol {f}}=\mathbb {M}_1^{-1}\boldsymbol{\cdot}\partial F/\partial {\boldsymbol {a}}}$
, such that evaluating (4.6) implies ${ {\boldsymbol {f}}=\mathbb {M}_1^{-1}\boldsymbol{\cdot}\partial F/\partial {\boldsymbol {a}}}$![]() . Therefore,
. Therefore,
The discrete variation ${\delta {\boldsymbol {Y}}=\delta {\boldsymbol {y}}\boldsymbol {\cdot }\mathbb {M}_1^{-1}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() establishes a similar result for $ {\boldsymbol {Y}}$
establishes a similar result for $ {\boldsymbol {Y}}$![]() , namely
, namely
Thus, to derive the discrete Poisson bracket, we substitute (4.7)–(4.8) into (4.2) and integrate over $\left | {\mathcal {T}_h} \right |$![]() to find
to find
True to its continuous counterpart in (4.2), the discrete Poisson bracket of (4.9) is in canonical symplectic form (i.e. Darboux coordinates).
4.2 The finite element Vlasov–Maxwell system
The full Poisson structure of the discrete Vlasov–Maxwell system readily follows from the foregoing analysis of its electromagnetic subsystem. To describe a system of $L$![]() particles, we let ${ {\boldsymbol {X}}_\ell, {\boldsymbol {P}}_\ell \in \mathbb {R}^{3}}$
particles, we let ${ {\boldsymbol {X}}_\ell, {\boldsymbol {P}}_\ell \in \mathbb {R}^{3}}$![]() ${\ell \in [1,L]}$
${\ell \in [1,L]}$![]() denote the position and momentum of the $\ell \textrm {th}$
denote the position and momentum of the $\ell \textrm {th}$![]() particle and let ${m_\ell }$
particle and let ${m_\ell }$![]() and ${q_\ell }$
and ${q_\ell }$![]() denote its mass and charge. Particles may then be characterized by a Klimontovich distribution, ${f( {\boldsymbol {x}}, {\boldsymbol {p}})=\sum _\ell \delta ( {\boldsymbol {x}}- {\boldsymbol {X}}_\ell )\delta ( {\boldsymbol {p}}- {\boldsymbol {P}}_\ell )}$
denote its mass and charge. Particles may then be characterized by a Klimontovich distribution, ${f( {\boldsymbol {x}}, {\boldsymbol {p}})=\sum _\ell \delta ( {\boldsymbol {x}}- {\boldsymbol {X}}_\ell )\delta ( {\boldsymbol {p}}- {\boldsymbol {P}}_\ell )}$![]() . Particle phase space is defined as usual with a canonical bracket on position ${ {\boldsymbol {X}}_\ell }$
. Particle phase space is defined as usual with a canonical bracket on position ${ {\boldsymbol {X}}_\ell }$![]() and momentum ${ {\boldsymbol {P}}_\ell }$
and momentum ${ {\boldsymbol {P}}_\ell }$![]() .
.
Combining (4.9) with the Poisson bracket for these $L$![]() particles, therefore, the discrete Vlasov–Maxwell Poisson structure is given by
particles, therefore, the discrete Vlasov–Maxwell Poisson structure is given by

Here, $F$![]() and $G$
and $G$![]() are arbitrary functionals on the discrete Poisson manifold ${(M_d,\{\cdot,\cdot \})}$
are arbitrary functionals on the discrete Poisson manifold ${(M_d,\{\cdot,\cdot \})}$![]() , where each point ${m_d\in M_d}$
, where each point ${m_d\in M_d}$![]() is defined by the data
is defined by the data
We now define a Hamiltonian ${H_\textrm {VM}=H_\textrm {VM}[ {\boldsymbol {a}}, {\boldsymbol {y}}, {\boldsymbol {X}}_i, {\boldsymbol {P}}_i]}$![]() on $M_d$
on $M_d$![]() , given in Gaussian units by
, given in Gaussian units by

where ${ {\boldsymbol {A}}( {\boldsymbol {X}}_\ell )= {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )}$![]() . In $H_\textrm {EM}$
. In $H_\textrm {EM}$![]() , we have substituted (3.5) and (4.3). The difference in $H_\textrm {Kinetic}$
, we have substituted (3.5) and (4.3). The difference in $H_\textrm {Kinetic}$![]() is taken componentwise, i.e. ${P_{\ell \mu }-(q_\ell /c) {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )_\mu }$
is taken componentwise, i.e. ${P_{\ell \mu }-(q_\ell /c) {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )_\mu }$![]() for ${\mu \in \{1,2,3\}}$
for ${\mu \in \{1,2,3\}}$![]() . Hereafter, we denote components of $ {\boldsymbol {P}}_\ell$
. Hereafter, we denote components of $ {\boldsymbol {P}}_\ell$![]() by $P_{\ell \mu }$
by $P_{\ell \mu }$![]() and those of $ {\boldsymbol {X}}_\ell$
and those of $ {\boldsymbol {X}}_\ell$![]() by $X_\ell ^{\mu }$
by $X_\ell ^{\mu }$![]() .
.
4.3 Gauge structure
We now examine the gauge structure of this discrete Vlasov–Maxwell system and derive its corresponding momentum map. We first note that, because ${\mathbb {C}\mathbb {G}=0}$![]() , $H_\textrm {VM}$
, $H_\textrm {VM}$![]() of (4.12) is invariant under any gauge transformation ${\varPhi _{\exp ( {\boldsymbol {s}})}:M_d\rightarrow M_d}$
of (4.12) is invariant under any gauge transformation ${\varPhi _{\exp ( {\boldsymbol {s}})}:M_d\rightarrow M_d}$![]() of the form
of the form

$\forall ~{\ell \in [1,L]}$![]() , ${ {\boldsymbol {s}}\in \mathbb {R}^{N_0}}$
, ${ {\boldsymbol {s}}\in \mathbb {R}^{N_0}}$![]() . Since ${\varPhi _{\exp ( {\boldsymbol {s}})}\circ \varPhi _{\exp ( {\boldsymbol {t}})}=\varPhi _{\exp ( {\boldsymbol {s}}+ {\boldsymbol {t}})}}$
. Since ${\varPhi _{\exp ( {\boldsymbol {s}})}\circ \varPhi _{\exp ( {\boldsymbol {t}})}=\varPhi _{\exp ( {\boldsymbol {s}}+ {\boldsymbol {t}})}}$![]() , such transformations form an abelian group. Evidently, they are also generated by vector fields ${X_{ {\boldsymbol {s}}}\in \mathfrak {X}(M_d)}$
, such transformations form an abelian group. Evidently, they are also generated by vector fields ${X_{ {\boldsymbol {s}}}\in \mathfrak {X}(M_d)}$![]() of the form
of the form

expressed using Einstein summation convention.
We may check whether $\varPhi$![]() of (4.13) is a canonical transformation, that is, whether it preserves the Poisson bracket of (4.10)
of (4.13) is a canonical transformation, that is, whether it preserves the Poisson bracket of (4.10)
$\forall \ {\boldsymbol {s}}$![]() . It suffices to check this condition infinitesimally, i.e. whether
. It suffices to check this condition infinitesimally, i.e. whether
After cancelling terms by the equality of mixed partials, verifying (4.16) reduces to checking that

Each term in this sum is seen to vanish, however, since
Thus, $X_{ {\boldsymbol {s}}}$![]() generates a canonical group action, as desired.
generates a canonical group action, as desired.
We now find the momentum map $\mu$![]() of this canonical group action by solving for its generating functions. In particular, given any ${ {\boldsymbol {s}}\in \mathbb {R}^{N_0}}$
of this canonical group action by solving for its generating functions. In particular, given any ${ {\boldsymbol {s}}\in \mathbb {R}^{N_0}}$![]() , we seek a generating function $\mu _{ {\boldsymbol {s}}}$
, we seek a generating function $\mu _{ {\boldsymbol {s}}}$![]() such that ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$
such that ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$![]() as derivations, as in (2.2). By comparing (4.10) and (4.14), we see that ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$
as derivations, as in (2.2). By comparing (4.10) and (4.14), we see that ${X_{ {\boldsymbol {s}}}=\{\cdot,\mu _{ {\boldsymbol {s}}}\}}$![]() holds if and only if
holds if and only if

Since ${\mathbb {G}^{T} { \boldsymbol {\varLambda }}^{1}=\mathrm {d} { \boldsymbol {\varLambda }}^{0}}$![]() is an exact form, this linear system of partial differential equations is readily solved by
is an exact form, this linear system of partial differential equations is readily solved by

The momentum map $\mu$![]() characterizing all generating functions $\{\mu _{ {\boldsymbol {s}}}\}$
characterizing all generating functions $\{\mu _{ {\boldsymbol {s}}}\}$![]() is defined by requiring that ${\mu \boldsymbol {\cdot } {\boldsymbol {s}}=\mu _{ {\boldsymbol {s}}}}\ \forall \ {\boldsymbol {s}}$
is defined by requiring that ${\mu \boldsymbol {\cdot } {\boldsymbol {s}}=\mu _{ {\boldsymbol {s}}}}\ \forall \ {\boldsymbol {s}}$![]() . Therefore, $\mu$
. Therefore, $\mu$![]() is given by
is given by

Setting ${\mu =0}$![]() , (4.21) is a discrete form of Gauss’ law,
, (4.21) is a discrete form of Gauss’ law,
where ${ {\boldsymbol {E}}=-4{\rm \pi} c {\boldsymbol {Y}}}$![]() and ${\rho =\sum _\ell q_\ell { \boldsymbol {\varLambda }}^{0}( {\boldsymbol {X}}_\ell )}$
and ${\rho =\sum _\ell q_\ell { \boldsymbol {\varLambda }}^{0}( {\boldsymbol {X}}_\ell )}$![]() .
.
Any non-zero value of $\mu$![]() indicates that the divergence of the electric field is not entirely accounted for by the dynamical particles labelled ${\ell \in [1,L]}$
indicates that the divergence of the electric field is not entirely accounted for by the dynamical particles labelled ${\ell \in [1,L]}$![]() . Since ${\dot {\mu }=0}$
. Since ${\dot {\mu }=0}$![]() , such a non-zero $\mu$
, such a non-zero $\mu$![]() acts as a fixed, external, non-dynamical background charge that persists throughout a simulation, and in a manner that remains entirely structure preserving. In particular, we may regard $\mu$
acts as a fixed, external, non-dynamical background charge that persists throughout a simulation, and in a manner that remains entirely structure preserving. In particular, we may regard $\mu$![]() as representing an external charge density,
as representing an external charge density,
As we shall demonstrate, (4.23) can be useful in establishing precise initial conditions in a PIC simulation.
5 Equations of motion
5.1 Continuous-time equations of motion
Let us now derive equations of motion via the Hamiltonian of (4.12) and the Poisson bracket of (4.10). We find

where ${ {\boldsymbol {A}}( {\boldsymbol {X}}_\ell )_\mu = {\boldsymbol {a}}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )_\mu }$![]() using the component notation of (3.3).
using the component notation of (3.3).
We remark that these equations of motion allow us to reexpress the conservation of the momentum map, ${\dot {\mu }=0}$![]() , as a discrete, local charge conservation law in conservative form. In particular, we may take the time derivative $\dot {\mu }$
, as a discrete, local charge conservation law in conservative form. In particular, we may take the time derivative $\dot {\mu }$![]() of (4.21) and substitute $\dot { {\boldsymbol {y}}}$
of (4.21) and substitute $\dot { {\boldsymbol {y}}}$![]() of (5.1), noting that ${\mathbb {C}\mathbb {G}=0}$
of (5.1), noting that ${\mathbb {C}\mathbb {G}=0}$![]() to find
to find
where ${\rho =\sum _\ell q_\ell { \boldsymbol {\varLambda }}^{0}( {\boldsymbol {X}}_\ell )}$![]() and ${ {\boldsymbol {j}}=\sum _\ell q_\ell \dot {X}^{\mu }_\ell { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )_\mu }$
and ${ {\boldsymbol {j}}=\sum _\ell q_\ell \dot {X}^{\mu }_\ell { \boldsymbol {\varLambda }}^{1}( {\boldsymbol {X}}_\ell )_\mu }$![]() . As in (4.21), we note a correspondence between the discrete and continuous operators ${\mathbb {G}^{T}\sim (-\boldsymbol {\nabla }\boldsymbol {\cdot })}$
. As in (4.21), we note a correspondence between the discrete and continuous operators ${\mathbb {G}^{T}\sim (-\boldsymbol {\nabla }\boldsymbol {\cdot })}$![]() . Thus, (5.2) is a discrete equivalent of the charge conservation law ${\partial _t{\rho }+\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {j}}=0}$
. Thus, (5.2) is a discrete equivalent of the charge conservation law ${\partial _t{\rho }+\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {j}}=0}$![]() , as seen in Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017).
, as seen in Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017).
Equation (5.1) is sometimes referred to as a semi-discrete system, since it describes a discretely defined system evolving in continuous time. We now proceed to a fully discrete, algorithmic system by defining a GCSM.
5.2 Discrete-time equations of motion via a gauge-compatible splitting
Using the Vlasov–Maxwell splitting discovered in He et al. (Reference He, Qin, Sun, Xiao, Zhang and Liu2015) and adapted to canonical coordinates in Glasser & Qin (Reference Glasser and Qin2020), we split $H_\textrm {VM}$![]() of (4.12) into five sub-Hamiltonians, as follows:
of (4.12) into five sub-Hamiltonians, as follows:

$\forall \ {\alpha \in \{x,y,z\}}$![]() . We immediately observe that each sub-Hamiltonian remains invariant under the gauge transformation $\varPhi _{\exp ( {\boldsymbol {s}})}$
. We immediately observe that each sub-Hamiltonian remains invariant under the gauge transformation $\varPhi _{\exp ( {\boldsymbol {s}})}$![]() defined in (4.13).
defined in (4.13).
Let us now examine the equations of motion of each subsystem, omitting equations for the subsystems’ static degrees of freedom

To clarify the notation in (5.4), we emphasize that, in the $H_{\textrm {Kinetic}}^{\alpha }$![]() subsystem, ${\dot {X}_\ell ^{\mu }=0}$
subsystem, ${\dot {X}_\ell ^{\mu }=0}$![]() for ${\mu \neq \alpha }$
for ${\mu \neq \alpha }$![]() . (Here, $\alpha$
. (Here, $\alpha$![]() is regarded as fixed while $\mu$
is regarded as fixed while $\mu$![]() ranges over all $\{{x,y,z}\}$
ranges over all $\{{x,y,z}\}$![]() indices.) Thus, the equations of motion for ${X}_\ell ^{\mu \neq \alpha }$
indices.) Thus, the equations of motion for ${X}_\ell ^{\mu \neq \alpha }$![]() are omitted above.
are omitted above.
Furthermore, it follows from a simple calculation that ${\ddot {X}_\ell ^{\alpha }=0}$![]() in $H_{\textrm {Kinetic}}^{\alpha }$
in $H_{\textrm {Kinetic}}^{\alpha }$![]() so that ${\dot {X}_\ell ^{\alpha }}$
so that ${\dot {X}_\ell ^{\alpha }}$![]() is constant during the evolution of each subsystem. As a result, all subsystems above are exactly integrable. Equation (5.4) therefore defines a GCSM.
is constant during the evolution of each subsystem. As a result, all subsystems above are exactly integrable. Equation (5.4) therefore defines a GCSM.
More concretely, an evolution over the timestep $[t,t+\varDelta ]$![]() in each subsystem is fully specified by
in each subsystem is fully specified by

In (5.5), $t$![]() is a fixed initial time and ${\delta \in [0,\varDelta ]}$
is a fixed initial time and ${\delta \in [0,\varDelta ]}$![]() parametrizes the particle trajectory ${ {\boldsymbol {X}}_\ell (t)\rightarrow {\boldsymbol {X}}_\ell (t+\varDelta )}$
parametrizes the particle trajectory ${ {\boldsymbol {X}}_\ell (t)\rightarrow {\boldsymbol {X}}_\ell (t+\varDelta )}$![]() during one timestep of the ${H_{\textrm {Kinetic}}^{\alpha }}$
during one timestep of the ${H_{\textrm {Kinetic}}^{\alpha }}$![]() subsystem, which forms a straight line segment in the $\hat {\alpha }$
subsystem, which forms a straight line segment in the $\hat {\alpha }$![]() direction. Since $ { \boldsymbol {\varLambda }}^{1}$
direction. Since $ { \boldsymbol {\varLambda }}^{1}$![]() is comprised of piecewise polynomial differential $\textrm {1-forms}$
is comprised of piecewise polynomial differential $\textrm {1-forms}$![]() , $ { \boldsymbol {\varLambda }}^{1}$
, $ { \boldsymbol {\varLambda }}^{1}$![]() and its derivatives are integrable in closed form along the straight path ${ {\boldsymbol {X}}_\ell (t+\delta )}$
and its derivatives are integrable in closed form along the straight path ${ {\boldsymbol {X}}_\ell (t+\delta )}$![]() . Thus, (5.5) defines a symplectic algorithm – specifically a GCSM – that can be computed exactly.
. Thus, (5.5) defines a symplectic algorithm – specifically a GCSM – that can be computed exactly.
6 Numerical examples
We now demonstrate the efficacy of this algorithm numerically. In § 6.1, we first consider a one-dimensional simulation of Landau damping electrons, choosing simulation parameters similar to those of Xiao et al. (Reference Xiao, Qin, Liu, He, Zhang and Sun2015), against a fixed, homogeneous, positive background charge. Then, in § 6.2, we reexpress the 1X2V simulation approach pursued in Crouseilles et al. (Reference Crouseilles, Einkemmer and Faou2015) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017) in canonical coordinates, thereby deriving the restriction of our algorithm to 1X2P phase space – comprised of one spatial dimension and two dimensions of canonical momentum. Finally, in § 6.3, we simulate the electromagnetic Weibel instability in this restricted phase space.
6.1 Landau damping
Using Whitney form finite elements, a 650-cell domain $\mathcal {T}_h$![]() with periodic boundaries is constructed. Each cell is assigned width ${w_x=2.4\times 10^{-2}\ \textrm {cm}}$
with periodic boundaries is constructed. Each cell is assigned width ${w_x=2.4\times 10^{-2}\ \textrm {cm}}$![]() , and ${26\times 10^{6}}$
, and ${26\times 10^{6}}$![]() electrons are simulated (40 000 per cell, when unperturbed). With electron temperature at ${T_e=5}$
electrons are simulated (40 000 per cell, when unperturbed). With electron temperature at ${T_e=5}$![]() keV, the set-up has Debye length ${\lambda _D=1.0\textrm { cm}}$
keV, the set-up has Debye length ${\lambda _D=1.0\textrm { cm}}$![]() and plasma frequency ${\omega _p=3.0\times 10^{9}\ \textrm {rad}\ \textrm {s}^{-1}}$
and plasma frequency ${\omega _p=3.0\times 10^{9}\ \textrm {rad}\ \textrm {s}^{-1}}$![]() , roughly mirroring physical parameters of Xiao et al. (Reference Xiao, Qin, Liu, He, Zhang and Sun2015).
, roughly mirroring physical parameters of Xiao et al. (Reference Xiao, Qin, Liu, He, Zhang and Sun2015).
We assume the electric field to have initial perturbation at ${t=0}$![]()
where ${E_0=1.2\ \textrm {statV}\ \textrm {cm}^{-1}}$![]() and ${k\lambda _D=0.8}$
and ${k\lambda _D=0.8}$![]() . To construct this perturbation, we first project the continuous 1-form field $ {\boldsymbol {Y}}_\textrm {cont}$
. To construct this perturbation, we first project the continuous 1-form field $ {\boldsymbol {Y}}_\textrm {cont}$![]() onto its Whitney form approximation, i.e. ${ {\boldsymbol {Y}}_\textrm {cont}\xrightarrow {{\rm \pi} _h} {\boldsymbol {Y}}= {\boldsymbol {y}}\boldsymbol {\cdot }\mathbb {M}_1^{-1}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$
onto its Whitney form approximation, i.e. ${ {\boldsymbol {Y}}_\textrm {cont}\xrightarrow {{\rm \pi} _h} {\boldsymbol {Y}}= {\boldsymbol {y}}\boldsymbol {\cdot }\mathbb {M}_1^{-1}\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() . In particular, we solve for $ {\boldsymbol {y}}$
. In particular, we solve for $ {\boldsymbol {y}}$![]() in (4.3) such that the integrals of ${ {\boldsymbol {Y}}_\textrm {cont}}$
in (4.3) such that the integrals of ${ {\boldsymbol {Y}}_\textrm {cont}}$![]() and $ {\boldsymbol {Y}}$
and $ {\boldsymbol {Y}}$![]() agree on edges of the discretized domain. This procedure yields a sinusoidal $\mu _\textrm {field}=\mathbb {G}^{T} {\boldsymbol {y}}$
agree on edges of the discretized domain. This procedure yields a sinusoidal $\mu _\textrm {field}=\mathbb {G}^{T} {\boldsymbol {y}}$![]() as depicted in figure 2.
as depicted in figure 2.

Figure 2. The terms of (4.21) are plotted over the simulation domain at time ${t=0}$![]() , characterizing initial conditions by the momentum map ${\mu =\mu _\textrm {field}+\mu _\textrm {particle}}$
, characterizing initial conditions by the momentum map ${\mu =\mu _\textrm {field}+\mu _\textrm {particle}}$![]() .
.
From the particle side, electron momenta are initialized in phase space by randomly selecting their velocities $\dot { {\boldsymbol {X}}}_\ell$![]() from a Maxwellian distribution of temperature ${T_e=5}$
from a Maxwellian distribution of temperature ${T_e=5}$![]() keV. Taking ${ {\boldsymbol {A}}=0}$
keV. Taking ${ {\boldsymbol {A}}=0}$![]() at ${t=0}$
at ${t=0}$![]() , initial canonical momenta are therefore given by ${ {\boldsymbol {P}}_\ell =m_\ell \dot { {\boldsymbol {X}}} _\ell }$
, initial canonical momenta are therefore given by ${ {\boldsymbol {P}}_\ell =m_\ell \dot { {\boldsymbol {X}}} _\ell }$![]() . Electron positions are then initialized to be consistent with Gauss’ law. More precisely, we demand that particle positions, in combination with the electric field perturbation, ensure the constancy of the total momentum map $\mu$
. Electron positions are then initialized to be consistent with Gauss’ law. More precisely, we demand that particle positions, in combination with the electric field perturbation, ensure the constancy of the total momentum map $\mu$![]() . Following (4.23), a non-zero constant momentum map can be understood as a fixed, homogeneous, ion background charge, ${\mu \sim \rho _\textrm {ext}/c}$
. Following (4.23), a non-zero constant momentum map can be understood as a fixed, homogeneous, ion background charge, ${\mu \sim \rho _\textrm {ext}/c}$![]() . Indeed, in a Landau damping simulation that takes only electrons to be dynamical, such a constant background charge constitutes the desired Gauss’ law remainder.
. Indeed, in a Landau damping simulation that takes only electrons to be dynamical, such a constant background charge constitutes the desired Gauss’ law remainder.
We therefore optimize electron positions $\{ {\boldsymbol {X}}_\ell \}$![]() to ensure ${\mu _\textrm {particle}=\sum _\ell ({\left | {e} \right |}/{c}) { \boldsymbol {\varLambda }}^{0}( {\boldsymbol {X}}_\ell )}$
to ensure ${\mu _\textrm {particle}=\sum _\ell ({\left | {e} \right |}/{c}) { \boldsymbol {\varLambda }}^{0}( {\boldsymbol {X}}_\ell )}$![]() closely satisfies
closely satisfies
where ${\mu _\textrm {field}=\mathbb {G}^{T} {\boldsymbol {y}}}$![]() and ${N_\textrm {ppc}=40\,000}$
and ${N_\textrm {ppc}=40\,000}$![]() denotes the number of particles per cell. In this way, the positive background charge, characterized by $\mu$
denotes the number of particles per cell. In this way, the positive background charge, characterized by $\mu$![]() , is homogeneous across the simulation domain and enforces quasineutrality with the dynamical electrons.
, is homogeneous across the simulation domain and enforces quasineutrality with the dynamical electrons.
This optimization of ${\mu _\textrm {particle}}$![]() is carried out in two stages. First, electrons are randomly selected via rejection sampling (von Neumann Reference von Neumann1951) from the distribution
is carried out in two stages. First, electrons are randomly selected via rejection sampling (von Neumann Reference von Neumann1951) from the distribution
which satisfies ${\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {E}}=4{\rm \pi} \left | {e} \right |(n_0-n_e)}$![]() . The electron positions ${\{ {\boldsymbol {X}}_\ell \}}$
. The electron positions ${\{ {\boldsymbol {X}}_\ell \}}$![]() are then further optimized using Nesterov accelerated gradient descent (Nesterov Reference Nesterov1983) to minimize the objective function
are then further optimized using Nesterov accelerated gradient descent (Nesterov Reference Nesterov1983) to minimize the objective function
The resulting momentum map, plotted in red in figure 2, thus defines a background charge that is homogeneous to a high degree of accuracy.
Note that an alternative initialization, undertaken for example by Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017), reverses the above procedure by randomly generating electron positions first and then solving for $ {\boldsymbol {y}}$![]() to satisfy Gauss’ law. This alternative is more straightforward computationally than the procedure described above, but it may afford less precision in the specification of the initial electric field perturbation, whenever such precision is desirable.
to satisfy Gauss’ law. This alternative is more straightforward computationally than the procedure described above, but it may afford less precision in the specification of the initial electric field perturbation, whenever such precision is desirable.
With initialized fields and electrons, the simulation is then evolved using a first-order Lie–Trotter splitting (Trotter Reference Trotter1959) derived from (5.5), in particular,
where ${ {\boldsymbol {u}}(t)}$![]() denotes the simulation state at time $t$
denotes the simulation state at time $t$![]() – i.e. ${ {\boldsymbol {u}}=m_d\in M_d}$
– i.e. ${ {\boldsymbol {u}}=m_d\in M_d}$![]() , a point in phase space as defined in (4.11).
, a point in phase space as defined in (4.11).
In figure 3, we first examine the evolution of the momentum map throughout the simulation domain. We note that, while $\mu _\textrm {particle}$![]() (multicolour) exhibits an oscillation and decay consistent with Landau damping, $\mu$
(multicolour) exhibits an oscillation and decay consistent with Landau damping, $\mu$![]() (grey) remains constant over time, consistent with the conservation of the momentum map.
(grey) remains constant over time, consistent with the conservation of the momentum map.

Figure 3. With their initial conditions as depicted in figure 2, the total momentum map $\mu$![]() (grey) is compared with $\mu _\textrm {particle}$
(grey) is compared with $\mu _\textrm {particle}$![]() (multicolour) as the two functions evolve over time. Whereas $\mu _\textrm {particle}$
(multicolour) as the two functions evolve over time. Whereas $\mu _\textrm {particle}$![]() exhibits a decaying sinusoid consistent with Landau damping, $\mu$
exhibits a decaying sinusoid consistent with Landau damping, $\mu$![]() remains constant to machine precision. The momentum map $\mu$
remains constant to machine precision. The momentum map $\mu$![]() constitutes a physical representation of the fixed positive background charge implicit in the simulation.
constitutes a physical representation of the fixed positive background charge implicit in the simulation.
To compare this simulation with theory, the evolution of the (normalized) electric field is plotted in figure 4 (which may be compared with figure 2 of Xiao et al. Reference Xiao, Qin, Liu, He, Zhang and Sun2015). The results agree with a theoretical expectation of (i) electrostatic Langmuir wave oscillation at a frequency ${\omega _p=3.0\times 10^{9}\ \textrm {rad}\ \textrm {s}^{-1}}$![]() , and (ii) Landau damping at a decay rate ${\omega _i={\omega _p}/{\kappa ^{3}}\sqrt {({{\rm \pi} }/{8})}\exp (-{(1+3\kappa ^{2})}/{2\kappa ^{2}})=3.9\times 10^{8} \textrm {rad}\ \textrm {s}^{-1}}$
, and (ii) Landau damping at a decay rate ${\omega _i={\omega _p}/{\kappa ^{3}}\sqrt {({{\rm \pi} }/{8})}\exp (-{(1+3\kappa ^{2})}/{2\kappa ^{2}})=3.9\times 10^{8} \textrm {rad}\ \textrm {s}^{-1}}$![]() , where ${\kappa =k\lambda _D}$
, where ${\kappa =k\lambda _D}$![]() . Furthermore, as is characteristic of a symplectic algorithm, the error in the total energy, measured by $H_\textrm {VM}$
. Furthermore, as is characteristic of a symplectic algorithm, the error in the total energy, measured by $H_\textrm {VM}$![]() of (4.12), is well bounded throughout the simulation. This error is plotted in figure 5.
of (4.12), is well bounded throughout the simulation. This error is plotted in figure 5.

Figure 4. The evolution of an electrostatic wave over time is simulated with a first-order Lie–Trotter splitting (Trotter Reference Trotter1959) of (5.5). The blue time series denotes the (normalized) log modulus of the electric field ${ {\boldsymbol {E}}=-4{\rm \pi} c {\boldsymbol {Y}}}$![]() , where ${\left | { {\boldsymbol {E}}} \right |}$
, where ${\left | { {\boldsymbol {E}}} \right |}$![]() is computed over the simulation domain by the ${L^{2}\varLambda ^{1}}$
is computed over the simulation domain by the ${L^{2}\varLambda ^{1}}$![]() norm. The theoretical Landau damping rate of the wave in a Maxwellian plasma is depicted as a red line, decaying at a rate of ${\omega _i={\omega _p}/{\kappa ^{3}}\sqrt {({{\rm \pi} }/{8})}\exp (-{(1+3\kappa ^{2})}/{2\kappa ^{2}})}$
norm. The theoretical Landau damping rate of the wave in a Maxwellian plasma is depicted as a red line, decaying at a rate of ${\omega _i={\omega _p}/{\kappa ^{3}}\sqrt {({{\rm \pi} }/{8})}\exp (-{(1+3\kappa ^{2})}/{2\kappa ^{2}})}$![]() for ${\kappa =k\lambda _D}$
for ${\kappa =k\lambda _D}$![]() .
.

Figure 5. The log error in the total energy of a first-order Lie–Trotter splitting (Trotter Reference Trotter1959) Landau damping simulation.
Having demonstrated the canonical finite element formalism's efficacy in simulating an electrostatic problem, we next consider the electromagnetic simulation of the Weibel instability. Before that, however, we introduce the ‘canonical 1X2P phase space’ in which we will conduct our simulation.
6.2 Canonical 1X2P phase space
Let us consider the restriction of phase space to one spatial dimension and two dimensions of canonical momentum. Despite its computational efficiency, the 1X2P setting is capable of simulating a number of non-trivial electromagnetic problems. Our development here of 1X2P phase space essentially adapts for canonical coordinates the techniques of Crouseilles et al. (Reference Crouseilles, Einkemmer and Faou2015) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017).
To characterize 1X2P, we must reflect the lack of $y$![]() dependence in the finite element expansions of our fields. In this setting, we therefore define $ {\boldsymbol {A}}$
dependence in the finite element expansions of our fields. In this setting, we therefore define $ {\boldsymbol {A}}$![]() and $ {\boldsymbol {Y}}$
and $ {\boldsymbol {Y}}$![]() by analogy with (4.3) as
by analogy with (4.3) as

Here, ${ {\boldsymbol {a}}_x}$![]() denotes a vector of coefficients that pair only with the finite element 1-form basis ${ { \boldsymbol {\varLambda }}^{1}(x)}$
denotes a vector of coefficients that pair only with the finite element 1-form basis ${ { \boldsymbol {\varLambda }}^{1}(x)}$![]() – a basis in 1X2P which has only $x$
– a basis in 1X2P which has only $x$![]() -components and whose spatial dependence is only one-dimensional. We further note that $ {\boldsymbol {a}}_y$
-components and whose spatial dependence is only one-dimensional. We further note that $ {\boldsymbol {a}}_y$![]() is defined as the coefficients of a 0-form. Since there is no way to associate 1-forms with $\hat {y}$
is defined as the coefficients of a 0-form. Since there is no way to associate 1-forms with $\hat {y}$![]() -directed edges in the 1X2P setting, 0-forms are the most natural representation of the $y$
-directed edges in the 1X2P setting, 0-forms are the most natural representation of the $y$![]() components of $ {\boldsymbol {A}}$
components of $ {\boldsymbol {A}}$![]() . This becomes especially clear when examining finite elements restricted to have spatial $x$
. This becomes especially clear when examining finite elements restricted to have spatial $x$![]() -dependence. The expansion of $ {\boldsymbol {Y}}$
-dependence. The expansion of $ {\boldsymbol {Y}}$![]() in (6.6) follows similarly, with appropriate mass matrices computed by integrals over the one-dimensional domain.
in (6.6) follows similarly, with appropriate mass matrices computed by integrals over the one-dimensional domain.
Turning now to the characterization of particle phase space, we retain two components of the canonical momentum, $P_{\ell x}$![]() and $P_{\ell y}$
and $P_{\ell y}$![]() . Only one component of spatial dependence is retained, which we shall denote $X_\ell$
. Only one component of spatial dependence is retained, which we shall denote $X_\ell$![]() .
.
The appropriate Hamiltonian is then computed by restricting (4.12) as follows:

We note that the term ${ {\boldsymbol {a}}_x\boldsymbol {\cdot }\mathbb {C}^{T}\mathbb {M}_2\mathbb {C}\boldsymbol {\cdot } {\boldsymbol {a}}_x}$![]() is absent; while it would ordinarily arise from the magnetic energy $|\mathrm {d} {\boldsymbol {A}}|^{2}$
is absent; while it would ordinarily arise from the magnetic energy $|\mathrm {d} {\boldsymbol {A}}|^{2}$![]() , $\mathrm {d}$
, $\mathrm {d}$![]() annihilates 1-forms in the 1X2P setting. Indeed, the magnetic field in the 1X2P formalism is given simply by ${ {\boldsymbol {B}}=\mathrm {d} {\boldsymbol {A}}= {\boldsymbol {a}}_y\boldsymbol {\cdot }\mathrm {d} { \boldsymbol {\varLambda }}^{0}=\mathbb {G} {\boldsymbol {a}}_y\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$
annihilates 1-forms in the 1X2P setting. Indeed, the magnetic field in the 1X2P formalism is given simply by ${ {\boldsymbol {B}}=\mathrm {d} {\boldsymbol {A}}= {\boldsymbol {a}}_y\boldsymbol {\cdot }\mathrm {d} { \boldsymbol {\varLambda }}^{0}=\mathbb {G} {\boldsymbol {a}}_y\boldsymbol {\cdot } { \boldsymbol {\varLambda }}^{1}}$![]() .
.
The Poisson bracket of the restricted phase space follows by simply omitting the inapplicable terms of (4.10). In particular

We observe that, despite its simplicity, the 1X2P phase space retains the gauge structure of the original problem. In particular we note its gauge symmetry

and the resulting momentum map

Finally, we derive the equations of motion in the 1X2P setting, which are straightforward reexpressions of their full phase space counterparts in (5.1)

Here, with an abuse of notation that ignores the non-existence of $Y_\ell$![]() , we define
, we define
We observe that $P_{\ell y}$![]() is conserved in (6.11), which can be viewed as a consequence of the independence from $Y_\ell$
is conserved in (6.11), which can be viewed as a consequence of the independence from $Y_\ell$![]() of the 1X2P formulation.
of the 1X2P formulation.
We further note that a gauge-compatible splitting of $H_\textrm {1X2P}$![]() is readily defined by the following four sub-Hamiltonians, in agreement with (5.3)
is readily defined by the following four sub-Hamiltonians, in agreement with (5.3)

Using the Poisson bracket ${\{\cdot,\cdot \}_\textrm {1X2P}}$![]() of (6.8), we thereby derive the following subsystem equations of motion:
of (6.8), we thereby derive the following subsystem equations of motion:

Since these equations of motion are – as (5.5) – exactly solvable, and since the sub-Hamiltonians of (6.13) preserve the gauge symmetry of (6.9), it is clear that (6.14) defines a GCSM that exactly preserves ${\mu _\textrm {1X2P}}$![]() .
.
6.3 Weibel instability
We now apply the 1X2P formulation defined above to the simulation of the Weibel instability. We initialize the simulation in close agreement with the parametrization of the Weibel instability simulations of Crouseilles et al. (Reference Crouseilles, Einkemmer and Faou2015) and Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017). Specifically, in a periodic domain of 64 cells we simulate ${N_e=100\,032}$![]() electrons. Continuing to work in Gaussian units, we take perturbation wavenumber ${k=1.25({\omega _p}/{c})}$
electrons. Continuing to work in Gaussian units, we take perturbation wavenumber ${k=1.25({\omega _p}/{c})}$![]() and simulation domain length $L=2{\rm \pi} /k$
and simulation domain length $L=2{\rm \pi} /k$![]() . We seed a magnetic perturbation by defining the vector potential to be
. We seed a magnetic perturbation by defining the vector potential to be
where ${B_0=-5.7\ \textrm {mG}}$![]() . We sample initial electron velocities from the anisotropic distribution
. We sample initial electron velocities from the anisotropic distribution

where ${\sigma _x=0.02c/\sqrt {2}}$![]() and ${\sigma _y=\sqrt {12}\sigma _x}$
and ${\sigma _y=\sqrt {12}\sigma _x}$![]() . To initialize the initial electron distribution to be independent of $x$
. To initialize the initial electron distribution to be independent of $x$![]() (i.e. spatially uniform) as above, we evenly space electrons throughout the simulation domain at separation of $L/N_e$
(i.e. spatially uniform) as above, we evenly space electrons throughout the simulation domain at separation of $L/N_e$![]() . $ {\boldsymbol {Y}}$
. $ {\boldsymbol {Y}}$![]() is correspondingly initialized to zero. $ {\boldsymbol {A}}$
is correspondingly initialized to zero. $ {\boldsymbol {A}}$![]() and $ {\boldsymbol {Y}}$
and $ {\boldsymbol {Y}}$![]() are again modelled using Whitney (0- and 1-) forms.
are again modelled using Whitney (0- and 1-) forms.
Finally, simulating the Weibel instability with a Lie–Trotter splitting of stepsize $1/40\omega _p$![]() yields the evolution plotted in figure 6. The magnetic field growth rate is in strong agreement with the analytic prediction (Weibel Reference Weibel1959),
yields the evolution plotted in figure 6. The magnetic field growth rate is in strong agreement with the analytic prediction (Weibel Reference Weibel1959),

Lastly, the total energy is also well bounded over the lifetime of the Weibel instability simulation, as depicted in figure 7.

Figure 6. The growth rate of the magnetic field energy closely approximates the analytic model of the Weibel instability. As the magnetic field ramps up, the anisotropy of the electron velocity is reduced. This plot may be compared with figure 1 of Kraus et al. (Reference Kraus, Kormann, Morrison and Sonnendrücker2017).

Figure 7. The log error in the total energy of a first-order Lie–Trotter splitting (Trotter Reference Trotter1959) Weibel instability simulation (Weibel Reference Weibel1959).
7 Conclusion
We have derived a canonical Poisson structure in (4.10) for the Vlasov–Maxwell system and constructed its Hamiltonian in (4.12) in the formalism of FEEC. Its gauge symmetry was studied to systematically derive the corresponding charge-conserving momentum map of (4.21). The resulting PIC algorithm of (5.5) was demonstrated to be a GCSM that preserves the momentum map to machine precision over the full simulation domain.
We have seen in (4.23) how the momentum map may be regarded as an external fixed charge in a PIC simulation. Using this interpretation, we optimized initial conditions for a Landau damping simulation that modelled a homogeneous positive fixed background, as depicted in figure 2. We explicitly demonstrated the preservation of this momentum map, as seen in figure 3.
The initialization procedure we described may be useful in future structure-preserving PIC simulations that require the precise initial specification of electric fields and background charge. Such a technique might be advantageous, for example, in the simulation of plasma interactions with charged plasma-facing components.
We further explored the efficacy of our gauge-compatible splitting algorithm by examining its restriction to 1X2P phase space, in which setting we simulated the Weibel instability. We demonstrated that the gauge structure of the full phase space has a counterpart in this sparser setting, and we accurately modelled the analytic growth rate of the Weibel instability in our simulation.
The flexibility of FEEC makes the algorithms defined in this paper significantly generalizable as well. For example, the PIC algorithm of this paper may be adapted to simulations on an unstructured mesh, including perhaps those defined in curvilinear coordinates.
However, it is worth noting an important drawback to the use of higher-order finite element spaces in the foregoing algorithms, namely, that their inverse mass matrices (e.g. $\mathbb {M}_1^{-1}$![]() in (5.4)) are not, in general, sparse. Dense inverse mass matrices necessitate global communication in every timestep of a simulation, significantly reducing the benefit of parallelization. Overcoming such a limitation would facilitate scalable, higher-order and higher-dimensional simulations – an effort that will be worthy of future study.
in (5.4)) are not, in general, sparse. Dense inverse mass matrices necessitate global communication in every timestep of a simulation, significantly reducing the benefit of parallelization. Overcoming such a limitation would facilitate scalable, higher-order and higher-dimensional simulations – an effort that will be worthy of future study.
Acknowledgements
The authors and Editor Luís O. Silva thank the referees for their advice in evaluating this article.
Funding
This research was supported by the U.S. Department of Energy (DE-AC02-09CH11466). This research was further supported by the U.S. Department of Energy Fusion Energy Sciences Postdoctoral Research Program administered by the Oak Ridge Institute for Science and Education (ORISE) for the DOE. ORISE is managed by Oak Ridge Associated Universities (ORAU) under DOE contract number DE-SC0014664. All opinions expressed in this paper are the authors’ and do not necessarily reflect the policies and views of DOE, ORAU, or ORISE.
Declaration of interests
The authors report no conflict of interest.
Author contributions
The authors contributed equally to theoretical development. A.S.G. performed the derivations and simulations.