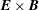Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T15:37:51.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Larmor radius effects on $\boldsymbol{E}\times \boldsymbol{B}$ weak turbulence transport

Part of: Focus on Fusion

Published online by Cambridge University Press:  01 May 2018

N. Kryukov ,
J. J. Martinell  and
D. del-Castillo-Negrete
N. Kryukov
Affiliation:
Instituto de Ciencias Nucleares, Universidad Nacional Autonoma de Mexico, A. Postal 70-543, 04510 Mexico D. F., Mexico
J. J. Martinell*
Affiliation:
Instituto de Ciencias Nucleares, Universidad Nacional Autonoma de Mexico, A. Postal 70-543, 04510 Mexico D. F., Mexico
D. del-Castillo-Negrete
Affiliation:
Oak Ridge National Laboratory, Oak Ridge, TN 37831-8071, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Transport of test particles in two-dimensional weak turbulence with waves propagating along the poloidal direction is studied using a reduced model. Finite Larmor radius (FLR) effects are included by gyroaveraging over one particle orbit. For low wave amplitudes the motion is mostly regular with particles trapped in the potential wells. As the amplitude increases the trajectories become chaotic and the Larmor radius modifies the orbits. For a thermal distribution of Finite Larmor radii the particle distribution function (PDF) is Gaussian for small 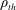$\unicode[STIX]{x1D70C}_{th}$ (thermal gyroradius) but becomes non-Gaussian for large $\unicode[STIX]{x1D70C}_{th}$. However, the time scaling of transport is diffusive, as characterized by a linear dependence of the variance of the PDF with time. An explanation for this behaviour is presented that provides an expression for an effective diffusion coefficient and reproduces the numerical results for large wave amplitudes which implies generalized chaos. When a shear flow is added in the direction of wave propagation, a modified model is obtained that produces free-streaming particle trajectories in addition to trapped ones; these contribute to ballistic transport for low wave amplitude but produce super-ballistic transport in the chaotic regime. As in the previous case, the PDF is Gaussian for low 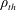$\unicode[STIX]{x1D70C}_{th}$ becoming non-Gaussian as it increases. The perpendicular transport presents the same behaviour as in the case with no flow but the diffusion is faster in the presence of the flow.

Keywords

plasma confinementplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 3 , June 2018 , 905840301
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Castillo-Negrete, D. 1998 Asymmetric transport and non-gaussian statistics of pasive scalars in vortices in shear. Phys. Fluids 10 (3), 576–594.CrossRefGoogle Scholar
del Castillo-Negrete, D. 2000 Chaotic transport in zonal flows in analogous geophysical and plasma systems. Phys. Plasmas 7 (5), 1702–1711.CrossRefGoogle Scholar
del Castillo-Negrete, D. & Morrison, P. J. 1993 Chaotic transport by Rosby waves in shear flow. Phys. Fluids A 5 (4), 948–965.CrossRefGoogle Scholar
Chôné, L., Beyer, P., Sarazin, Y., Fuhr, G., Bourdelle, C. & Benkadda, S. 2015 Mechanisms and dynamics of the external transport barrier formation in non-linear plasma edge simulations. Nucl. Fusion 55 (7), 073010.CrossRefGoogle Scholar
Dewhurst, J. M., Hnat, B. & Dendy, R. O. 2010 Finite larmor radius effects on test particle transport in drift wave-zonal flow turbulence. Plasma Phys. Control. Fusion 52 (1), 025004.CrossRefGoogle Scholar
da Fonseca, J. D., del Castillo-Negrete, D. & Caldas, I. L. 2014 Area-preserving maps models of gyoaveraged exb chaotic transport. Phys. Plasmas 21 (9), 092310.CrossRefGoogle Scholar
da Fonseca, J. D., del Castillo-Negrete, D., Sokolov, I. M. & Caldas, I. L. 2016 A statistical study of gyro-averaged effects in a reduced model of drift-wave transport. Phys. Plasmas 23 (8), 082308.CrossRefGoogle Scholar
Garbet, X., Idomura, Y., Villard, L. & Watanbe, T. H. 2010 Gyrokinetic simulations of turbulent transport. Nucl. Fusion 50, 043002.CrossRefGoogle Scholar
Gustafson, K., del Castillo-Negrete, D. & Dorland, W. 2008 Finite larmor radius effects on nondiffusive tracer transport in a zonal flow. Phys. Plasmas 15, 102309.CrossRefGoogle Scholar
Horton, W. 2017 Turbulent Transport in Magnetized Plasmas, 2nd edn. World Scientific Publishing Co.CrossRefGoogle Scholar
Horton, W., Park, H.-B., Kwon, J.-M., Strozzi, D., Morrison, P. J. & Choi, D.-I. 1998 Drift wave test particle transport in reversed shear profile. Phys. Plasmas 5 (11), 3910–3917.CrossRefGoogle Scholar
Karney, C. F. F. 1979 Stochastic ion heating by a lower hybrid wave: Ii. Phys. Fluids 22 (11), 2188–2209.CrossRefGoogle Scholar
Kleva, R. G. & Drake, J. F. 1984 Stochastic exb particle transport. Phys. Fluids 27, 1686–1698.CrossRefGoogle Scholar
Lee, W. W. 1987 Gyrokinetic particle simulation model. J. Comput. Phys. 72, 243–269.CrossRefGoogle Scholar
Lichtenberg, A. J. & Lieberman, M. A. 1992 Regular and Chaotic Dynamics. Springer.CrossRefGoogle Scholar
Manfredi, G. & Dendy, R. O. 1997 Transport properties of energeric particles in a turbulent electrostatic field. Phys. Plasmas 4 (3), 628–635.CrossRefGoogle Scholar
Martinell, J. J. & del Castillo-Negrete, D. 2013 Gyroaverage effects on chaotic transport by drift waves in zonal flows. Phys. Plasmas 20, 022303.CrossRefGoogle Scholar