Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T02:58:40.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast and spectrally accurate evaluation of gyroaverages in non-periodic gyrokinetic-Poisson simulations

Part of: Focus on Fusion

Published online by Cambridge University Press:  22 August 2017

J. Guadagni  and
A. J. Cerfon
J. Guadagni
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
A. J. Cerfon*
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a fast and spectrally accurate numerical scheme for the evaluation of the gyroaveraged electrostatic potential in non-periodic gyrokinetic-Poisson simulations. Our method relies on a reformulation of the gyrokinetic-Poisson system in which the gyroaverage in Poisson’s equation is computed for the compactly supported charge density instead of the non-periodic, non-compactly supported potential itself. We calculate this gyroaverage with a combination of two Fourier transforms and a Hankel transform, which has the near optimal run-time complexity 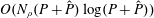$O(N_{\unicode[STIX]{x1D70C}}(P+\hat{P})\log (P+\hat{P}))$, where 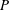$P$ is the number of spatial grid points, 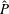$\hat{P}$ the number of grid points in Fourier space and 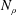$N_{\unicode[STIX]{x1D70C}}$ the number of grid points in velocity space. We present numerical examples illustrating the performance of our code and demonstrating geometric convergence of the error.

Keywords

intense particle beamsmagnetized plasmasplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 4 , August 2017 , 905830407
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonsen, T. M. & Lane, B. 1980 Kinetic equations for low frequency instabilities in inhomogeneous plasmas. Phys. Fluids 23, 1205–1214.Google Scholar
Brizard, A. J. & Hahm, T. S. 2007 Foundations of nonlinear gyrokinetic theory. Rev. Mod. Phys. 79, 421–468.Google Scholar
Candy, J. & Waltz, R. E. 2003 An Eulerian gyrokinetic-Maxwell solver. J. Comput. Phys. 186, 545–581.Google Scholar
Catto, P. J. 1978 Linearized gyro-kinetics. Plasma Phys. 20, 719.Google Scholar
Catto, P. J. & Tsang, K. T. 1977 Linearized gyrokinetic equation with collisions. Phys. Fluids 20, 396–401.Google Scholar
Cerfon, A. J. 2016 Vortex dynamics and shear layer instability in high intensity cyclotrons. Phys. Rev. Lett. 116, 174801.Google Scholar
Cerfon, A. J., Freidberg, J. P., Parra, F. I. & Antaya, T. A. 2013 Analytic fluid theory of beam spiraling in high-intensity cyclotrons. Phys. Rev. Accel. Beams 16, 024202.Google Scholar
Crouseilles, N., Mehrenberger, M. & Sellama, H. 2010 Numerical solution of the gyroaverage operator for the finite gyroradius guiding-center model. Commun. Comput. Phys. 8, 484–510.Google Scholar
Davis, C. 1962 The norm of the Schur product operation. Numer. Math. 4, 343.Google Scholar
Dutt, A. & Rokhlin, V. 1993 Fast Fourier transforms for nonequispaced data. SIAM J. Sci. Comput. 1, 121.Google Scholar
Frieman, E. A. & Chen, L. 1982 Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria. Phys. Fluids 25, 502–508.Google Scholar
Garbet, X., Idomura, Y., Villard, L. & Watanabe, T. H. 2010 TOPICAL REVIEW: Gyrokinetic simulations of turbulent transport. Nucl. Fusion 50, 043002.Google Scholar
Genovese, L., Deutsch, T., Neelov, A., Goedecker, S. & Beylkin, G. 2006 Efficient solution of Poissons equation with free boundary conditions. J. Chem. Phys. 125, 074105.Google Scholar
Görler, T., Lapillonne, X., Brunner, S., Dannert, T., Jenko, F., Merz, F. & Told, D. 2011 The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 230, 7053–7071.Google Scholar
Greengard, L. & Lee, J.-Y. 2004 Accelerating the nonuniform fast Fourier transform. SIAM Rev. 46, 443.Google Scholar
Greengard, L., Lee, J.-Y. & Inati, S. 2006 The fast sinc transform and image reconstruction from nonuniform samples in k-space. CAMCoS 1, 121.CrossRefGoogle Scholar
Guadagni, J.2015 Numerical solver for the two-dimensional Vlasov–Poisson equations in gyrokinetic variables. PhD thesis, Courant Institute of Mathematical Sciences, New York University.Google Scholar
Hardy, G. H. 1933 A theorem concerning Fourier transforms. J. London Math. Soc. 8, 227–231.Google Scholar
Hazeltine, R. D. & Meiss, J. D. 2003 Plasma Confinement. Courier Dover Publications.Google Scholar
Hogan, J. A. & Lakey, J. D. 2005 Time Frequency and Time-Scale Methods. Adaptive Decompositions, Uncertainty Principles, and Sampling. Birkhauser.Google Scholar
Jiang, S., Greengard, L. & Bao, W. 2014 Fast and accurate evaluation of nonlocal coulomb and dipole–dipole interactions via the nonuniform FFT. SIAM J. Sci. Comput. 36, B777–B794.Google Scholar
Jolliet, S., Bottino, A., Angelino, P., Hatzky, R., Tran, T. M., Mcmillan, B. F., Sauter, O., Appert, K., Idomura, Y. & Villard, L. 2007 A global collisionless PIC code in magnetic coordinates. J. Comput. Phys. 177, 409–425.Google Scholar
Lee, J.-Y. & Greengard, L. 2005 The type 3 nonuniform FFT and its applications. J. Comput. Phys. 206, 1.Google Scholar
Marburg, S. 2008 Discretisation requirements: How many elements per wavelength are necessary? In Computational Acoustics of Noise Propagation in Fluids – Finite and Boundary Element Methods (ed. Marburg, S. & Nolte, B.), pp. 309–332. Springer.Google Scholar
Numata, R., Howes, G. G, Tatsuno, T., Barnes, M. & Dorland, W. 2010 AstroGK: Astrophysical gyrokinetics code. J. Comput. Phys. 229, 9347–9372.CrossRefGoogle Scholar
Pataki, A. & Greengard, L. 2011 Fast elliptic solvers in cylindrical coordinates and the Coulomb collision operator. J. Comput. Phys. 230, 7840–7852.Google Scholar
Peterson, J. L. & Hammett, G. W. 2013 Positivity preservation and advection algorithms with applications to edge plasma turbulence. SIAM J. Sci. Comput. 35, B576–B605.Google Scholar
Plunk, G. G., Cowley, S. C., Schekochihin, A. A. & Tatsuno, T. 2010 Two-dimensional gyrokinetic turbulence. J. Fluid Mech. 664, 407–435.Google Scholar
Ricketson, L. F. & Cerfon, A. J. 2017 Sparse grid techniques for particle-in-cell schemes. Plasma Phys. Control. Fusion 59, 024002.Google Scholar
Rutherford, P. H. & Frieman, E. A. 1968 Drift instabilities in general magnetic field configurations. Phys. Fluids 11, 569–585.Google Scholar
Sarazin, Y., Grandgirard, V., Fleurence, E., Garbet, X., Ghendrih, P., Bertrand, P. & Depret, G. 2005 Kinetic features of interchange turbulence. Plasma Phys. Control. Fusion 47, 1817–1839.Google Scholar
Shu, C.-W. 1999 High order ENO and WENO schemes for computational fluid dynamics. In High-Order Methods for Computational Physics (ed. Barth, T. J. & Deconinck, H.). Springer.Google Scholar
Stein, E. M. & Shakarchi, R. 2003 Complex Analysis, Princeton Lectures in Analysis, vol. II.. Princeton University Press.Google Scholar
Steiner, C., Mehrenberger, M., Crouseilles, N., Grandgirard, V., Latu, G. & Rozar, F. 2015 Gyroaverage operator for a polar mesh. Eur. Phys. J. D 69, 18.Google Scholar
Taylor, J. B. & Hastie, R. J. 1968 Stability of general plasma equilibria. Part I. Formal theory. Plasma Phys. 10, 479–494.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics.Google Scholar
Trefethen, L. N. 2008 Is Gauss quadrature better than Clenshaw–Curtis? SIAM Rev. 50, 67.Google Scholar
Trefethen, L. N. 2013 Approximation Theory and Approximation Practice. Society for Industrial and Applied Mathematics.Google Scholar
Trefethen, L. N. & Weideman, J. A. C. 2014 The exponentially convergent trapezoidal rule. SIAM Rev. 56, 385.Google Scholar
Vico, F., Greengard, L. & Ferrando, M. 2016 Fast convolution with free-space Green’s functions. J. Comput. Phys. 323, 191–203.Google Scholar
Wilkening, J., Cerfon, A. J. & Landreman, M. 2015 Projected dynamics of kinetic equations with energy diffusion in spaces of orthogonal polynomials. J. Comput. Phys. 294, 58–77.Google Scholar