Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strait, E. J.
King, J. D.
Hanson, J. M.
and
Logan, N. C.
2016.
Spatial and temporal analysis of DIII-D 3D magnetic diagnostic data.
Review of Scientific Instruments,
Vol. 87,
Issue. 11,
Hanson, J.M.
Berkery, J.W.
Bialek, J.
Clement, M.
Ferron, J.R.
Garofalo, A.M.
Holcomb, C.T.
La Haye, R.J.
Lanctot, M.J.
Luce, T.C.
Navratil, G.A.
Olofsson, K.E.J.
Strait, E.J.
Turco, F.
and
Turnbull, A.D.
2017.
Stability of DIII-D high-performance, negative central shear discharges.
Nuclear Fusion,
Vol. 57,
Issue. 5,
p.
056009.
Brunetti, Daniele
Graves, J. P.
Lazzaro, E.
Mariani, A.
Nowak, S.
Cooper, W. A.
and
Wahlberg, C.
2018.
Analytic study on low- external ideal infernal modes in tokamaks with large edge pressure gradients.
Journal of Plasma Physics,
Vol. 84,
Issue. 2,
Paz-Soldan, C
Eidietis, N W
Liu, Y Q
Shiraki, D
Boozer, A H
Hollmann, E M
Kim, C C
and
Lvovskiy, A
2019.
Kink instabilities of the post-disruption runaway electron beam at low safety factor.
Plasma Physics and Controlled Fusion,
Vol. 61,
Issue. 5,
p.
054001.
Paz-Soldan, C.
Reux, C.
Aleynikova, K.
Aleynikov, P.
Bandaru, V.
Beidler, M.
Eidietis, N.
Liu, Y.Q.
Liu, C.
Lvovskiy, A.
Silburn, S.
Bardoczi, L.
Baylor, L.
Bykov, I.
Carnevale, D.
Del-Castillo Negrete, D.
Du, X.
Ficker, O.
Gerasimov, S.
Hoelzl, M.
Hollmann, E.
Jachmich, S.
Jardin, S.
Joffrin, E.
Lasnier, C.
Lehnen, M.
Macusova, E.
Manzanares, A.
Papp, G.
Pautasso, G.
Popovic, Z.
Rimini, F.
Shiraki, D.
Sommariva, C.
Spong, D.
Sridhar, S.
Szepesi, G.
Zhao, C.
DIII-D Team, the
and
Contributors, JET
2021.
A novel path to runaway electron mitigation via deuterium injection and current-driven MHD instability.
Nuclear Fusion,
Vol. 61,
Issue. 11,
p.
116058.
Lao, Lang L.
Liu, Y.Q.
and
Turnbull, Alan D.
2021.
Encyclopedia of Nuclear Energy.
p.
431.
Battey, A.F.
Hanson, J.M.
Bialek, J.
Turco, F.
Navratil, G.A.
and
Logan, N.C.
2023.
Simultaneous stabilization and control of the n = 1 and n = 2 resistive wall mode.
Nuclear Fusion,
Vol. 63,
Issue. 6,
p.
066025.
Wang, Y.Q.
Hao, G.Z.
Zou, Y.P.
Liu, Y.Q.
Chen, W.
Yang, G.M.
Meng, G.
Miao, Y.T.
Zhao, Y.F.
and
Xia, Y.B.
2023.
Effects of external kink and fishbone-like modes on energetic particle transport in tokamak plasmas.
Nuclear Fusion,
Vol. 63,
Issue. 2,
p.
026003.
Liu, Yueqiang
Aleynikova, K.
Hollmann, E. M.
Paz-Soldan, C.
Aleynikov, P.
Khayrutdinov, R.
and
Lukash, V.
2023.
Diffusion–convection model of runaway electrons due to large magnetohydrodynamic perturbations in post-thermal quench plasmas.
Physics of Plasmas,
Vol. 30,
Issue. 9,
Paz-Soldan, C.
Chrystal, C.
Lunia, P.
Nelson, A.O.
Thome, K.E.
Austin, M.E.
Cote, T.B.
Hyatt, A.W.
Leuthold, N.
Marinoni, A.
Osborne, T.H.
Pharr, M.
Sauter, O.
Scotti, F.
Wilks, T.M.
and
Wilson, H.S.
2024.
Simultaneous access to high normalized density, current, pressure, and confinement in strongly-shaped diverted negative triangularity plasmas.
Nuclear Fusion,
Vol. 64,
Issue. 9,
p.
094002.
Shen, Yong
Dong, Jiaqi
He, Hongda
Li, Jia
Wu, Na
Zhao, Kaijun
and
Deng, Wei
2024.
Study of Ideal Magnetohydrodynamic Operational β Limit of the HL-2A Tokamak.
Journal of the Physical Society of Japan,
Vol. 93,
Issue. 10,
Zheng, Linjin
Kotschenreuther, M. T.
Waelbroeck, F. L.
and
Austin, M. E.
2025.
X-point effects on the ideal MHD modes in tokamaks in the description of dual-poloidal-region safety factor.
Physics of Plasmas,
Vol. 32,
Issue. 1,
Wang, C.
Nardon, E.
Artola, F.J.
Bandaru, V.
and
Hoelzl, M.
2025.
The effect of vertical displacements on the runaway electron avalanche in ITER mitigated disruptions.
Nuclear Fusion,
Vol. 65,
Issue. 1,
p.
016012.
 $q$ at the 95 % poloidal flux surface,
$q$ at the 95 % poloidal flux surface, 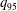 $q_{95}$ , is driven below 2.0. The instability is a resistive kink counterpart to the current-driven ideal mode that traditionally explained the corresponding disruption in limited cross-sections (Shafranov, Sov. Phys. Tech. Phys., vol. 15, 1970, p. 175) when
$q_{95}$ , is driven below 2.0. The instability is a resistive kink counterpart to the current-driven ideal mode that traditionally explained the corresponding disruption in limited cross-sections (Shafranov, Sov. Phys. Tech. Phys., vol. 15, 1970, p. 175) when 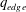 $q_{edge}$ , the safety factor at the outermost closed flux surface, lies just below a rational value
$q_{edge}$ , the safety factor at the outermost closed flux surface, lies just below a rational value 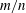 $m/n$ . Experimentally, external kink modes are observed in limiter configurations as the current in a tokamak is ramped up and
$m/n$ . Experimentally, external kink modes are observed in limiter configurations as the current in a tokamak is ramped up and 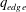 $q_{edge}$ decreases through successive rational surfaces. For
$q_{edge}$ decreases through successive rational surfaces. For  $q_{edge}<2$ , the instability is always encountered and is highly disruptive. However, diverted plasmas, in which
$q_{edge}<2$ , the instability is always encountered and is highly disruptive. However, diverted plasmas, in which 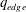 $q_{edge}$ is formally infinite in the magnetohydrodynamic (MHD) model, have presented a longstanding difficulty since the theory would predict stability, yet, the disruptive limit occurs in practice when
$q_{edge}$ is formally infinite in the magnetohydrodynamic (MHD) model, have presented a longstanding difficulty since the theory would predict stability, yet, the disruptive limit occurs in practice when 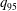 $q_{95}$ , reaches 2. It is shown from numerical calculations that a resistive kink mode is linearly destabilized by the rapidly increasing resistivity at the plasma edge when
$q_{95}$ , reaches 2. It is shown from numerical calculations that a resistive kink mode is linearly destabilized by the rapidly increasing resistivity at the plasma edge when 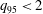 $q_{95}<2$ , but
$q_{95}<2$ , but 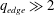 $q_{edge}\gg 2$ . The resistive kink behaves much like the ideal kink with predominantly kink or interchange parity and no real sign of a tearing component. However, the growth rates scale with a fractional power of the resistivity near the
$q_{edge}\gg 2$ . The resistive kink behaves much like the ideal kink with predominantly kink or interchange parity and no real sign of a tearing component. However, the growth rates scale with a fractional power of the resistivity near the 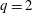 $q=2$ surface. The results have a direct bearing on the conventional edge cutoff procedures used in most ideal MHD codes, as well as implications for ITER and for future reactor options.
$q=2$ surface. The results have a direct bearing on the conventional edge cutoff procedures used in most ideal MHD codes, as well as implications for ITER and for future reactor options.