Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-12T08:27:44.928Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy cascade rate in isothermal compressible magnetohydrodynamic turbulence

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  18 July 2018

N. Andrés Open the ORCID record for N. Andrés [Opens in a new window] ,
F. Sahraoui ,
S. Galtier ,
L. Z. Hadid ,
P. Dmitruk  and
P. D. Mininni
N. Andrés*
Affiliation:
Laboratoire de Physique des Plasmas, École Polytechnique, CNRS, Sorbonne University, Observatoire de Paris, Univ. Paris-Sud, F-91128 Palaiseau CEDEX, France
F. Sahraoui
Affiliation:
Laboratoire de Physique des Plasmas, École Polytechnique, CNRS, Sorbonne University, Observatoire de Paris, Univ. Paris-Sud, F-91128 Palaiseau CEDEX, France
S. Galtier
Affiliation:
Laboratoire de Physique des Plasmas, École Polytechnique, CNRS, Sorbonne University, Observatoire de Paris, Univ. Paris-Sud, F-91128 Palaiseau CEDEX, France Univ. Paris-Sud, Université Paris-Saclay, France
L. Z. Hadid
Affiliation:
Swedish Institute of Space Physics, Uppsala, Sweden
P. Dmitruk
Affiliation:
Instituto de Física de Buenos Aires, CONICET-UBA, Ciudad Universitaria, 1428, Buenos Aires, Argentina
P. D. Mininni
Affiliation:
Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria, 1428, Buenos Aires, Argentina
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

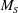Three-dimensional direct numerical simulations are used to study the energy cascade rate in isothermal compressible magnetohydrodynamic turbulence. Our analysis is guided by a two-point exact law derived recently for this problem in which flux, source, hybrid and mixed terms are present. The relative importance of each term is studied for different initial subsonic Mach numbers $M_{S}$ and different magnetic guide fields 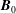$\boldsymbol{B}_{0}$ . The dominant contribution to the energy cascade rate comes from the compressible flux, which depends weakly on the magnetic guide field 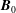$\boldsymbol{B}_{0}$ , unlike the other terms whose moduli increase significantly with 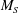$M_{S}$ and 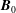$\boldsymbol{B}_{0}$ . In particular, for strong 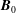$\boldsymbol{B}_{0}$ the source and hybrid terms are dominant at small scales with almost the same amplitude but with a different sign. A statistical analysis undertaken with an isotropic decomposition based on the SO(3) rotation group is shown to generate spurious results in the presence of 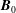$\boldsymbol{B}_{0}$ , when compared with an axisymmetric decomposition better suited to the geometry of the problem. Our numerical results are compared with previous analyses made with in situ measurements in the solar wind and the terrestrial magnetosheath.

Keywords

plasma nonlinear phenomenaplasma simulationspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 4 , August 2018 , 905840404
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrés, N., Clark di Leoni, P., Mininni, P. D., Dmitruk, P., Sahraoui, F. & Matthaeus, W. H. 2017 Interplay between Alfvén and magnetosonic waves in compressible magnetohydrodynamics turbulence. Phys. Plasmas 24 (10), 102314.Google Scholar
Andrés, N., Galtier, S. & Sahraoui, F. 2016a Exact scaling laws for helical three-dimensional two-fluid turbulent plasmas. Phys. Rev. E 94 (6), 063206.Google Scholar
Andrés, N., Galtier, S. & Sahraoui, F. 2018 Exact law for homogeneous compressible Hall magnetohydrodynamics turbulence. Phys. Rev. E 97, 013204.Google Scholar
Andrés, N., Mininni, P. D., Dmitruk, P. & Gomez, D. O. 2016b von Kármán–Howarth equation for three-dimensional two-fluid plasmas. Phys. Rev. E 93 (6), 063202.Google Scholar
Andrés, N. & Sahraoui, F. 2017 Alternative derivation of exact law for compressible and isothermal magnetohydrodynamics turbulence. Phys. Rev. E 96 (5), 053205.Google Scholar
Arad, I., Biferale, L., Mazzitelli, I. & Procaccia, I. 1999 Disentangling scaling properties in anisotropic and inhomogeneous turbulence. Phys. Rev. Lett. 82 (25), 5040.Google Scholar
Banerjee, S. & Galtier, S. 2013 Exact relation with two-point correlation functions and phenomenological approach for compressible magnetohydrodynamic turbulence. Phys. Rev. E 87 (1), 013019.Google Scholar
Banerjee, S. & Galtier, S. 2014 A Kolmogorov-like exact relation for compressible polytropic turbulence. J. Fluid Mech. 742, 230–242.Google Scholar
Banerjee, S., Hadid, L. Z., Sahraoui, F. & Galtier, S. 2016 Scaling of compressible magnetohydrodynamic turbulence in the fast solar wind. Astrophys. J. Lett. 829 (2), L27.Google Scholar
Banerjee, S. & Kritsuk, A. G. 2018a Energy transfer in compressible magnetohydrodynamic turbulence for isothermal self-gravitating fluids. Phys. Rev. E 97 (2), 023107.Google Scholar
Banerjee, S. & Kritsuk, A. G. 2018b Energy transfer in compressible magnetohydrodynamic turbulence for isothermal self-gravitating fluids. Phys. Rev. E 97, 023107.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneus Turbulence. Cambridge University Press.Google Scholar
Bhattacharjee, A., Huang, Y.-M., Yang, H. & Rogers, B. 2009 Fast reconnection in high-lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16 (11), 112102.Google Scholar
Biferale, L. & Toschi, F. 2001 Anisotropic homogeneous turbulence: hierarchy and intermittency of scaling exponents in the anisotropic sectors. Phys. Rev. Lett. 86 (21), 4831.Google Scholar
Brunt, C. M., Federrath, C. & Price, D. J. 2010 A method for reconstructing the variance of a 3D physical field from 2D observations: application to turbulence in the interstellar medium. Mon. Not. R. Astron. Soc. 403 (3), 1507–1515.CrossRefGoogle Scholar
Carbone, V., Marino, R., Sorriso-Valvo, L., Noullez, A. & Bruno, R. 2009 Scaling laws of turbulence and heating of fast solar wind: the role of density fluctuations. Phys. Rev. Lett. 103 (6), 061102.Google Scholar
Chandrasekhar, S. 1951 The invariant theory of isotropic turbulence in magneto-hydrodynamics. Proc. R. Soc. Lond. A 204 (1079), 435–449.Google Scholar
Dmitruk, P., Matthaeus, W. H. & Oughton, S. 2005 Direct comparisons of compressible magnetohydrodynamics and reduced magnetohydrodynamics turbulence. Phys. Plasmas 12 (11), 112304.CrossRefGoogle Scholar
Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible euler and Navier–Stokes equations. Nonlinearity 13 (1), 249.CrossRefGoogle Scholar
Eyink, G. L. & Drivas, T. D. 2018 Cascades and dissipative anomalies in compressible fluid turbulence. Phys. Rev. X 8, 011022.Google Scholar
Federrath, C. 2016 Magnetic field amplification in turbulent astrophysical plasmas. J. Plasma Phys. 82 (6), 535820601.Google Scholar
Federrath, C. & Banerjee, S. 2015 The density structure and star formation rate of non-isothermal polytropic turbulence. Mon. Not. R. Astron. Soc. 448 (4), 3297–3313.Google Scholar
Federrath, C. & Klessen, R. S. 2012 The star formation rate of turbulent magnetized clouds: comparing theory, simulations, and observations. Astrophys. J. 761 (2), 156.Google Scholar
Federrath, C., Rathborne, J. M., Longmore, S. N., Kruijssen, J. M. D., Bally, J., Contreras, Y., Crocker, R. M., Garay, G., Jackson, J. M., Testi, L. et al. 2017 The Multi-Messenger Astrophysics of the Galactic Centre (ed. Crocker, R. M., Longmore, S. N. & Bicknell, G. V.), vol. 322, pp. 123–128. IAU Symposium.Google Scholar
Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W. & Mac Low, M.-M. 2010 Comparing the statistics of interstellar turbulence in simulations and observations. Solenoidal versus compressive turbulence forcing. Astron. Astrophys. 512, A81.Google Scholar
Fitzpatrick, R. 2014 Plasma Physics: An Introduction. CRC Press.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Galtier, S. 2018 On the origin of the energy dissipation anomaly in (Hall) magnetohydrodynamics. J. Phys. A 51 (20), 205501.Google Scholar
Galtier, S. & Banerjee, S. 2011 Exact relation for correlation functions in compressible isothermal turbulence. Phys. Rev. Lett. 107 (13), 134501.Google Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63 (5), 447–488.CrossRefGoogle Scholar
Ghosh, S., Hossain, M. & Matthaeus, W. H. 1993 The application of spectral methods in simulating compressible fluid and magnetofluid turbulence. Comput. Phys. Commun. 74 (1), 18–40.Google Scholar
Gómez, D. O., Mininni, P. D. & Dmitruk, P. 2005 Parallel Simulations in Turbulent MHD. Phys. Scr. T116, 123–127.Google Scholar
Grete, P., O’Shea, B. W., Beckwith, K., Schmidt, W. & Christlieb, A. 2017 Energy transfer in compressible magnetohydrodynamic turbulence. Phys. Plasmas 24 (9), 092311.Google Scholar
Hadid, L., Sahraoui, F., Galtier, S. & Huang, S. 2018 Compressible magnetohydrodynamic turbulence in the Earth’s magnetosheath: estimation of the energy cascade rate using in situ spacecraft data. Phys. Rev. Lett. 120, 055102.CrossRefGoogle ScholarPubMed
Hadid, L. Z., Sahraoui, F. & Galtier, S. 2017 Energy cascade rate in compressible fast and slow solar wind turbulence. Astrophys. J. 838 (1), 9.Google Scholar
Imazio, P. R. & Mininni, P. D. 2011 Anomalous scaling of passive scalars in rotating flows. Phys. Rev. E 83 (6), 066309.Google Scholar
Imazio, P. R. & Mininni, P. D. 2017 Passive scalars: mixing, diffusion, and intermittency in helical and nonhelical rotating turbulence. Phys. Rev. E 95 (3), 033103.Google Scholar
de Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kritsuk, A. G., Wagner, R. & Norman, M. L. 2013 Energy cascade and scaling in supersonic isothermal turbulence. J. Fluid Mech. 729, R1.Google Scholar
Kurien, S., L’vov, V. S., Procaccia, I. & Sreenivasan, K. R. 2000b Scaling structure of the velocity statistics in atmospheric boundary layers. Phys. Rev. E 61 (1), 407.Google Scholar
Kurien, S. & Sreenivasan, K. R. 2000a Anisotropic scaling contributions to high-order structure functions in high-Reynolds-number turbulence. Phys. Rev. E 62 (2), 2206.Google Scholar
Low, M.-M. M. 1999 The energy dissipation rate of supersonic, magnetohydrodynamic turbulence in molecular clouds. Astrophys. J. 524 (1), 169.Google Scholar
Marino, R., Sorriso-Valvo, L., Carbone, V., Noullez, A., Bruno, R. & Bavassano, B. 2008 Heating the solar wind by a magnetohydrodynamic turbulent energy cascade. Astrophys. J. Lett. 677, L71–L74.Google Scholar
Marsch, E. & Mangeney, A. 1987 Ideal MHD equations in terms of compressive elsasser variables. J. Geophys. Res. 92 (A7), 7363–7367.Google Scholar
Martin, L. N. & Mininni, P. D. 2010 Intermittency in the isotropic component of helical and nonhelical turbulent flows. Phys. Rev. E 81 (1), 016310.Google Scholar
Matthaeus, W. H., Ghosh, S., Oughton, S. & Roberts, D. A. 1996 Anisotropic three-dimensional MHD turbulence. J. Geophys. Res. 101 (A4), 7619–7629.Google Scholar
Matthaeus, W. H. & Goldstein, M. L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87 (A8), 6011–6028.Google Scholar
Meyrand, R., Galtier, S. & Kiyani, K. H. 2016 Direct evidence of the transition from weak to strong magnetohydrodynamic turbulence. Phys. Rev. Lett. 116, 105002.Google Scholar
Mininni, P. D. & Pouquet, A. 2009 Finite dissipation and intermittency in magnetohydrodynamics. Phys. Rev. E 80, 025401.Google Scholar
Mininni, P. D. & Pouquet, A. 2010 Rotating helical turbulence. I. Global evolution and spectral behavior. Phys. Fluids 22 (3), 035105.Google Scholar
Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI-OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37 (6–7), 16–326.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT.Google Scholar
Nolan, C. A., Federrath, C. & Sutherland, R. S. 2015 The density variance–mach number relation in isothermal and non-isothermal adiabatic turbulence. Mon. Not. R. Astron. Soc. 451 (2), 1380–1389.Google Scholar
Oughton, S., Matthaeus, W. H., Wan, M. & Parashar, T. 2016 Variance anisotropy in compressible 3-D MHD. J. Geophys. Res. 121, 5041–5054.Google Scholar
Oughton, S., Wan, M., Servidio, S. & Matthaeus, W. H. 2013 On the origin of anisotropy in magnetohydrodynamic turbulence: The role of higher-order correlations. Astrophys. J. 768 (1), 10.Google Scholar
Passot, T. & Vázquez-Semadeni, E. 1998 Density probability distribution in one-dimensional polytropic gas dynamics. Phys. Rev. E 58, 4501–4510.Google Scholar
Politano, H. & Pouquet, A. 1998a Dynamical length scales for turbulent magnetized flows. Geophys. Res. Lett. 25 (3), 273–276.Google Scholar
Politano, H. & Pouquet, A. 1998b von Kármán–Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 57 (1), R21.Google Scholar
Sahraoui, F. 2008 Diagnosis of magnetic structures and intermittency in space-plasma turbulence using the technique of surrogate data. Phys. Rev. E 78, 026402.Google Scholar
Shebalin, J. V., Matthaeus, W. H. & Montgomery, D. 1983 Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 29 (03), 525–547.Google Scholar
Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., Veltri, P., Bruno, R., Bavassano, B. & Pietropaolo, E. 2007 Observation of inertial energy cascade in interplanetary space plasma. Phys. Rev. Lett. 99 (11), 115001.Google Scholar
Sujovolsky, N. E. & Mininni, P. D. 2016 Tridimensional to bidimensional transition in magnetohydrodynamic turbulence with a guide field and kinetic helicity injection. Phys. Rev. Fluids 1, 054407.Google Scholar
Taylor, M. A., Kurien, S. & Eyink, G. L. 2003 Recovering isotropic statistics in turbulence simulations: The Kolmogorov $4/5$ th law. Phys. Rev. E 68 (2), 026310.Google Scholar
Wan, M., Oughton, S., Servidio, S. & Matthaeus, W. H. 2012 von Kármán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. J. Fluid Mech. 697, 296–315.Google Scholar
Wan, M., Servidio, S., Oughton, S. & Matthaeus, W. H. 2010 The third-order law for magnetohydrodynamic turbulence with shear: numerical investigation. Phys. Plasmas 17 (5), 052307.Google Scholar
Weygand, J. M., Matthaeus, W. H., Dasso, S., Kivelson, M. G. & Walker, R. J. 2007 Taylor scale and effective magnetic Reynolds number determination from plasma sheet and solar wind magnetic field fluctuations. J. Geophys. Res. 112, A10.Google Scholar
Yang, Y., Matthaeus, W. H., Parashar, T. N., Haggerty, C. C., Roytershteyn, V., Daughton, W., Wan, M., Shi, Y. & Chen, S. 2017 Energy transfer, pressure tensor, and heating of kinetic plasma. Phys. Plasmas 24 (7), 072306.CrossRefGoogle Scholar
Yoshimatsu, K. 2012 Examination of the four-fifths law for longitudinal third-order moments in incompressible magnetohydrodynamic turbulence in a periodic box. Phys. Rev. E 85, 066313.Google Scholar
Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R. & Telloni, D. 2017a Theory and transport of nearly incompressible magnetohydrodynamic turbulence. Astrophys. J. 835 (2), 147.Google Scholar
Zank, G. P., Du, S. & Hunana, P. 2017b The origin of compressible magnetic turbulence in the very local interstellar medium. Astrophys. J. 842 (2), 114.Google Scholar
Zank, G. P. & Matthaeus, W. H. 1990 Nearly incompressible hydrodynamics and heat conduction. Phys. Rev. Lett. 64 (11), 1243.Google Scholar