Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T15:00:33.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Electron temperature resonances of a plasma column described to full first order in the temperature

Published online by Cambridge University Press:  13 March 2009

R. Koch  and
P. E. Vandenplas
R. Koch
Affiliation:
Laboratoire de Physique des Plasmas, Association ‘Euratom-Etat Beige’, Ecole Royalo Militaire
P. E. Vandenplas
Affiliation:
Laboratorium voor Plasmafysica Associatie ‘Euaratom-Belgische Staat’, Koninklijke Militaire School, 1040 Brussels
Get access Rights & Permissions [Opens in a new window]

Abstract

An inhomogeneous plasma column surrounded by a glass wall is described through full first order in temperatures Te and Ti using a complete electromagnetic treatment. We study the response of this system to a purely TE wave with K perpendicular to the axis. Comparison with existing theories and experimental results is made in the electron–wave domain (ions play no role) with zero steady magnetic field, i.e. in the case of temperature (Tonks-Dattner) resonances. Perhaps surprising at first sight, there is poor agreement with experiment at low density, the classic T½e theory (scalar perturbed pressure approximation) giving far better results. Simple arguments concerning the different levels of approximation in the description of the longitudinal k2 enable us to distinguish the crucial difference existing between a scalar pressure and a complete T description and to understand this result. We generalize these findings, demoastrating that a 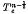description is always more realistic than a 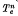one in the range ωpe<ω.

Type
Research Article
Information
Journal of Plasma Physics , Volume 11 , Issue 3 , June 1974 , pp. 451 - 460
Copyright
Copyright © Cambridge University Press 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Azevedo, J. C. 1966 Ph.D. thesis, Massachusetts Institute of Technology.Google Scholar
Ballieu, R., Messiarn, A. M. & Vandenflas, P. E. 1972 J. Plasma Phys. 8, 113.CrossRefGoogle Scholar
Baldwin, D. E. 1967 J. Plasma Phys. 1, 289.CrossRefGoogle Scholar
Buchsbaum, S. J. & Hasegawa, A. 1964 Phys. Rev. Lett. 12, 685.CrossRefGoogle Scholar
Buchsbaum, S. J. & Hasegawa, A. 1966 Phys. Rev. 143, 303.CrossRefGoogle Scholar
Crawford, F. W. 1963 Phys. Lett. 5, 244.CrossRefGoogle Scholar
Dattner, A. 1957 Ericsson Technics, 2, 309.Google Scholar
Gould, R. W. 1960 Bull. Am. Phys. Soc. 5, 322.Google Scholar
Ignat, D. W. 1969 Ph.D. thesis, Yale University.Google Scholar
Ignat, D. W. 1970 Phys. Fluids, 13, 1771.CrossRefGoogle Scholar
Monfort, J.-L. 1970 Laboratoire de Physique des Plasinas, Ecole Royale Militaire, Rep. 43.Google Scholar
Monfort, J.-L. & Vandenplas, P. E. 1970 Phys. Lett. 31A, 11.CrossRefGoogle Scholar
Monfort, J. -L. & Vandexplas, P. E. 1972 Transport Theory and Statistical Phys. 2, 1.CrossRefGoogle Scholar
Romell, D. 1951 Nature, 167, 243.CrossRefGoogle Scholar
Parker, J. V., Nickel, J. C. & Gould, R. W. 1964 Phys. F1uids, 7, 1489.Google Scholar
Sivasubramanian, A. & Tang, T. 1972 Phys. Rev. 6, 2257.CrossRefGoogle Scholar
Tonks, L. 1931 a Phys. Rev. 37, 1458.CrossRefGoogle Scholar
Tonks, L. 1931 b Phys. Rev. 38, 1219.CrossRefGoogle Scholar
Vandenplas, P. E. 1961 D.Sc. thesis, University of Brussels.Google Scholar
Vandenplas, P. E. 1968 Electron Waves and Resonances in Bounded Plasmas. Interscience.Google Scholar
Vandenplas, P. E. & Messiaen, A. M. 1964 Plasma Phys. 6, 459.Google Scholar