Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T13:17:03.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Eikonal-Glauber Thomas–Fermi model for atomic collisions with many-electron atoms for plasma applications

Published online by Cambridge University Press:  25 June 2018

Myoung-Jae Lee  and
Young-Dae Jung Open the ORCID record for Young-Dae Jung [Opens in a new window]
Myoung-Jae Lee
Affiliation:
Department of Physics, Hanyang University, Seoul 04763, South Korea Research Institute for Natural Sciences, Hanyang University, Seoul 04763, South Korea
Young-Dae Jung
Affiliation:
Department of Electrical and Computer Engineering, MC 0407, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0407, USA Department of Applied Physics and Department of Bionanotechnology, Hanyang University, Ansan, Kyunggi-Do 15588, South Korea
Get access Rights & Permissions [Opens in a new window]

Abstract

We have derived the universal eikonal-Glauber Thomas–Fermi model for atomic collision cross-sections with many-electron atoms, such as iron and tungsten atoms, including the influence of atomic screening in fusion devices and plasma technologies. The eikonal-Glauber method is employed to obtain the analytic expressions for the effective atomic charge, the scattering phase shift and the atomic cross-section in terms of the atomic form factor and the Mott–Massey screening parameter. The result shows that the effective atomic charge would be the same as the case of the net nuclear charge for the large momentum transfer domain and becomes zero without momentum transfer due to the influence of bound atomic electrons. It is shown that the eikonal scattering phase shift and the total eikonal-Glauber scattering cross-section increase with increasing charge number 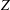$Z$ of the nucleus of the target atom. It is also found that the charge dependence of the total eikonal-Glauber scattering cross-section decreases with an increase of the scaled collision energy since the atomic form factor is small for large collision energies.

Keywords

fusion plasmaplasma applications
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 3 , June 2018 , 905840313
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbari-Moghanjoughi, M. 2013 Shukla–Eliasson attractive force: revisited. J. Plasma Phys. 79, 189.CrossRefGoogle Scholar
Akbari-Moghanjoughi, M. 2014a Coupled Langmuir oscillations in 2-dimensional quantum plasmas. Phys. Plasmas 21, 032110.Google Scholar
Akbari-Moghanjoughi, M. 2014b Maximal Cherenkov $\unicode[STIX]{x1D6FE}$ -radiation on Fermi-surface of compact stars. Phys. Plasmas 21, 053301.CrossRefGoogle Scholar
Akbari-Moghanjoughi, M. 2015 Hydrodynamic limit of Wigner–Poisson kinetic theory: revisited. Phys. Plasmas 22, 022103.Google Scholar
Baimbetov, F. B., Nurekenov, Kh. T. & Ramazanov, T. S. 1995 Pseudopotential theory of classical non-ideal plasmas. Phys. Lett. A 202, 211.Google Scholar
Bartschat, K. 2013 Computational methods for electron–atom collisions in plasma applications. J. Phys. D: Appl. Phys. 46, 334004.Google Scholar
Bethe, H. A. & Salpeter, E. E. 1957 Quantum Mechanics of One- and Two-Electron Atoms. Springer.CrossRefGoogle Scholar
Burke, P. G. & Joachain, C. J. 1995 Theory of Electron–Atom Collisions, Part 1: Potential Scattering. Plenum.Google Scholar
Chang, W.-S. & Jung, Y.-D. 2007 Quantum-mechanical effects on polarization elastic electron–atom collisions in partially ionized dense hydrogen plasmas. Phys. Scr. 76, 299.Google Scholar
Chen, F. F. 2016 Introduction to Plasma Physics and Controlled Fusion, 3rd edn. Springer.Google Scholar
Friedrich, H. 2017 Theoretical Atomic Physics, 4th edn. Springer.CrossRefGoogle Scholar
Jamil, M., Shahid, M., Zeba, I., Salimullah, M., Shah, H. A. & Murtaza, G. 2012 Quantum modification of dust shear Alfvén wave in plasmas. Phys. Plasmas 19, 023705.Google Scholar
Joachain, C. J. 1983 Quantum Collision Theory, 3rd edn. North Holland.Google Scholar
Jung, Y.-D. & Lee, K.-S. 1995 Screening effects on nonrelativistic bremsstrahlung in the scattering of electrons by neutral atoms. Astrophys. J. 440, 830.Google Scholar
Mott, N. F. & Massey, H. S. 1987 The Theory of Atomic Collisions, vol. II, 3rd edn. Oxford University Press.Google Scholar
Omarbakiyeva, Y. A., Ramazanov, T. S. & Röpke, G. 2009 The electron–atom interaction in partially ionized dense plasmas. J. Phys. A: Math. Gen. 42, 214045.Google Scholar
Osterbrock, D. E. & Ferland, G. J. 2006 Astrophysics of Gaseous Nebulae and Active Galactic Nuclei, 2nd edn. University Science Books.Google Scholar
Pandey, M. K., Lin, Y.-C. & Ho, Y. K. 2012 Cross sections of charge exchange and ionization in $\text{O}^{8+}+\text{H}$ collision in Debye plasmas. Phys. Plasmas 19, 062104.Google Scholar
Pandey, M. K., Lin, Y.-C. & Ho, Y. K. 2013 Investigation of charge transfer and ionization in He-like systems ( $\text{Li}^{+}$ , $\text{Be}^{2+}$ , $\text{B}^{3+}$ , $\text{C}^{4+}$ , $\text{N}^{5+}$ , $\text{O}^{6+}$ )-hydrogen atom collisions in Debye plasmas. Phys. Plasmas 20, 022104.Google Scholar
Pavlov, G. A. 2000 Transport Processes in Plasmas with Strong Coulomb Interaction. Gordon and Breach.Google Scholar
Ramazanov, T. S., Dzhumagulova, K. N. & Gabdullin, M. T. 2006 Microscopic and thermodynamic properties of dense semiclassical partially ionized hydrogen plasma. J. Phys. A: Math. Gen. 39, 4469.Google Scholar
Ramazanov, T. S., Dzhumagulova, K. N. & Gabdullin, M. T. 2010 Effective potentials for ion–ion and charge–atom interactions of dense semiclassical plasma. Phys. Plasmas 17, 042703.Google Scholar
Ramazanov, T. S., Dzhumagulova, K. N., Omarbakiyeva, Y. A. & Röpke, G. 2006 Effective polarization interaction potentials of the partially ionized dense plasma. J. Phys. A: Math. Gen. 39, 4369.Google Scholar
Ramazanov, T. S., Moldabekov, ZH. A., Dzhumagulova, K. N. & Muratov, M. M. 2011 Pseudopotentials of the particles interactions in complex plasmas. Phys. Plasmas 18, 103705.Google Scholar
Ramazanov, T. S., Moldabekov, ZH. A., Gabdullin, M. T. & Ismagambetova, T. N. 2014 Interaction potentials and thermodynamic properties of two component semiclassical plasma. Phys. Plasmas 21, 012706.CrossRefGoogle Scholar
Schwinger, J. 2001 Quantum Mechanics. Springer.Google Scholar
Shevelko, V. P. 1997 Atoms and Their Spectroscopic Properties. Springer.Google Scholar
Shevelko, V. P. & Tawara, H. 1995 Semiempirical formulae for multiple ionization of neutral atoms and positive ions by electron impact. J. Phys. B 28, L589.Google Scholar
Shevelko, V. P. & Tawara, H. 1998 Atomic Multielectron Processes. Springer.Google Scholar
Sivia, D. S. 2011 Elementary Scattering Theory. Oxford University Press.Google Scholar
Smirnov, B. M. 2007 Plasma Processes and Plasma Kinetics. Wiley-VCH.Google Scholar
Song, M.-Y., Litsarev, M. S., Shevelko, V. P., Tawara, H. & Yoon, J.-S. 2009 Single- and multiple-electron loss cross-sections for fast heavy ions colliding with neutrals: semi-classical calculations. Nucl. Instrum. Meth. B 267, 2369.Google Scholar
Weinberg, S. 2015 Lectures on Quantum Mechanics, 2nd edn. Cambridge University Press.Google Scholar
Zatsarinny, O. & Bartschat, K. 2013 The $B$ -spline $R$ -matrix method for atomic processes: application to atomic structure, electron collisions and photoionization. J. Phys. B 46, 112001.Google Scholar