Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-07-01T07:43:59.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficient kinetic Lattice Boltzmann simulation of three-dimensional Hall-MHD turbulence

Published online by Cambridge University Press:  08 August 2023

Raffaello Foldes Open the ORCID record for Raffaello Foldes [Opens in a new window] ,
Emmanuel Lévêque Open the ORCID record for Emmanuel Lévêque [Opens in a new window] ,
Raffaele Marino Open the ORCID record for Raffaele Marino [Opens in a new window] ,
Ermanno Pietropaolo Open the ORCID record for Ermanno Pietropaolo [Opens in a new window] ,
Alessandro De Rosis Open the ORCID record for Alessandro De Rosis [Opens in a new window] ,
Daniele Telloni Open the ORCID record for Daniele Telloni [Opens in a new window]  and
Fabio Feraco Open the ORCID record for Fabio Feraco [Opens in a new window]
Raffaello Foldes*
Affiliation:
Univ Lyon, CNRS, École Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon I, LMFA UMR 5509, F-69134 Ecully cedex, France Dipartimento di Scienze Fisiche e Chimiche, Università dell'Aquila, 67100 Coppito (AQ), Italy
Emmanuel Lévêque
Affiliation:
Univ Lyon, CNRS, École Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon I, LMFA UMR 5509, F-69134 Ecully cedex, France
Raffaele Marino
Affiliation:
Univ Lyon, CNRS, École Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon I, LMFA UMR 5509, F-69134 Ecully cedex, France
Ermanno Pietropaolo
Affiliation:
Dipartimento di Scienze Fisiche e Chimiche, Università dell'Aquila, 67100 Coppito (AQ), Italy
Alessandro De Rosis
Affiliation:
Department of Mechanical, Aerospace and Civil Engineering, The University of Manchester, Manchester M13 9PL, UK
Daniele Telloni
Affiliation:
National Institute for Astrophysics – Astrophysical Observatory of Torino, Via Osservatorio 20, I-10025 Pino Torinese, Italy
Fabio Feraco
Affiliation:
Univ Lyon, CNRS, École Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon I, LMFA UMR 5509, F-69134 Ecully cedex, France Leibniz Institute of Atmospheric Physics at the University of Rostock, Schlossstrasse 6, Kühlungsborn 18225, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Simulating plasmas in the Hall-magnetohydrodynamics (Hall-MHD) regime represents a valuable approach for the investigation of complex nonlinear dynamics developing in astrophysical frameworks and fusion machines. The Hall electric field is computationally very challenging as it involves the integration of an additional term, proportional to $\boldsymbol {\nabla } \times ((\boldsymbol {\nabla }\times \boldsymbol {B})\times \boldsymbol {B})$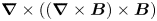, in Faraday's induction law. The latter feeds back on the magnetic field $B$ 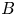at small scales (between the ion and electron inertial scales), requiring very high resolutions in both space and time to properly describe its dynamics. The computational advantage provided by the kinetic lattice Boltzmann (LB) approach is exploited here to develop a new code, the fast lattice-Boltzmann algorithm for MHD experiments (flame). The flame code integrates the plasma dynamics in lattice units coupling two kinetic schemes, one for the fluid protons (including the Lorentz force), the other to solve the induction equation describing the evolution of the magnetic field. Here, the newly developed algorithm is tested against an analytical wave-solution of the dissipative Hall-MHD equations, pointing out its stability and second-order convergence, over a wide range of the control parameters. Spectral properties of the simulated plasma are finally compared with those obtained from numerical solutions from the well-established pseudo-spectral code ghost. Furthermore, the LB simulations we present, varying the Hall parameter, highlight the transition from the MHD to the Hall-MHD regime, in excellent agreement with the magnetic field spectra measured in the solar wind.

Keywords

space plasma physicsplasma simulationplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 89 , Issue 4 , August 2023 , 905890413
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adhikari, L., Zank, G.P., Bruno, R., Telloni, D., Hunana, P., Dosch, A., Marino, R. & Hu, Q. 2015 a The transport of low-frequency turbulence in astrophysical flows. II. Solutions for the super-Alfvénic solar wind. Astrophys. J. 805 (1), 63.CrossRefGoogle Scholar
Adhikari, L., Zank, G.P., Bruno, R., Telloni, D., Hunana, P., Dosch, A., Marino, R. & Hu, Q. 2015 b The transport of low-frequency turbulence in the super-Alfvénic solar wind. J. Phys.: Conf. Ser. 642 (1), 012001.Google Scholar
Alexandrova, O., Lacombe, C. & Mangeney, A. 2008 Spectra and anisotropy of magnetic fluctuations in the Earth's magnetosheath: cluster observations. Ann. Geophys. 26 (11), 3585–3596.CrossRefGoogle Scholar
Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S.J. & Robert, P. 2009 Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103, 165003.CrossRefGoogle ScholarPubMed
Andrés, N., Sahraoui, F., Huang, S., Hadid, L.Z. & Galtier, S. 2022 The incompressible energy cascade rate in anisotropic solar wind turbulence. Astron. Astrophys. 661, A116.CrossRefGoogle Scholar
Bale, S.D., Badman, S.T., Bonnell, J.W., Bowen, T.A., Burgess, D., Case, A.W., Cattell, C.A., Chandran, B.D.G., Chaston, C.C., Chen, C.H.K., et al. 2019 Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 576 (7786), 237–242.CrossRefGoogle ScholarPubMed
Bale, S.D., Goetz, K., Harvey, P.R., Turin, P., Bonnell, J.W., Dudok de Wit, T., Ergun, R.E., MacDowall, R.J., Pulupa, M., Andre, M., et al. 2016 The FIELDS instrument suite for Solar Probe Plus. Measuring the coronal plasma and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 204 (1–4), 49–82.CrossRefGoogle ScholarPubMed
Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222 (3), 145–197.CrossRefGoogle Scholar
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.CrossRefGoogle Scholar
Bouchut, F. 1999 Construction of BGK models with a family of kinetic entropies for a given system of conservation laws. J. Stat. Phys. 95, 113–170.CrossRefGoogle Scholar
Breyiannis, G. & Valougeorgis, D. 2004 Lattice kinetic simulations in three-dimensional magnetohydrodynamics. Phys. Rev. E 69, 065702.CrossRefGoogle ScholarPubMed
Breyiannis, G. & Valougeorgis, D. 2006 Lattice kinetic simulations of 3-D MHD turbulence. Comput. Fluids 35, 920–924.CrossRefGoogle Scholar
Brodiano, M., Dmitruk, P. & Andrés, N. 2023 A statistical study of the compressible energy cascade rate in solar wind turbulence: parker solar probe observations. Phys. Plasmas 30 (3), 032903.CrossRefGoogle Scholar
Bruno, R. & Carbone, V. 2013 The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10 (1), 2.CrossRefGoogle Scholar
Bruno, R. & Trenchi, L. 2014 Radial dependence of the frequency break between fluid and kinetic scales in the solar wind fluctuations. Astrophys. J. Lett. 787 (2), L24.CrossRefGoogle Scholar
Bruno, R., Trenchi, L. & Telloni, D. 2014 Spectral slope variation at proton scales from fast to slow solar wind. Astrophys. J. Lett. 793 (1), L15.CrossRefGoogle Scholar
Cerri, S.S., Califano, F., Jenko, F., Told, D. & Rincon, F. 2016 Subproton-scale cascades in solar wind turbulence: driven hybrid-kinetic simulations. Astrophys. J. Lett. 822 (1), L12.CrossRefGoogle Scholar
Chen, S., Chen, H., Martnez, D. & Matthaeus, W. 1991 Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 67, 3776–3779.CrossRefGoogle ScholarPubMed
Coreixas, C., Chopard, B. & Latt, J. 2019 Comprehensive comparison of collision models in the lattice Boltzmann framework: theoretical investigations. Phys. Rev. E 100, 033305.CrossRefGoogle ScholarPubMed
Coreixas, C., Wissocq, G., Puigt, G., Boussuge, J.-F. & Sagaut, P. 2017 Recursive regularization step for high-order lattice Boltzmann methods. Phys. Rev. E 96 (3), 033306.CrossRefGoogle ScholarPubMed
Croisille, J.P., Khanfir, R. & Chanteu, G. 1995 Numerical simulation of the MHD equations by a kinetic-type method. J. Sci. Comput. 10, 81–92.CrossRefGoogle Scholar
D'Amicis, R., Bruno, R., Panasenco, O., Telloni, D., Perrone, D., Marcucci, M.F., Woodham, L., Velli, M., De Marco, R., Jagarlamudi, V., et al. 2021 First Solar Orbiter observation of the Alfvénic slow wind and identification of its solar source. Astron. Astrophys. 656, A21.CrossRefGoogle Scholar
De Rosis, A. 2017 Nonorthogonal central-moments-based lattice Boltzmann scheme in three dimensions. Phys. Rev. E 95, 013310.CrossRefGoogle ScholarPubMed
De Rosis, A., Lévêque, E. & Chahine, R. 2018 Advanced lattice Boltzmann scheme for high-Reynolds-number magneto-hydrodynamic flows. J. Turbul. 19 (6), 446–462.CrossRefGoogle Scholar
De Rosis, A. & Luo, K.H. 2019 Role of higher-order Hermite polynomials in the central-moments-based lattice Boltzmann framework. Phys. Rev. E 99 (1), 013301.CrossRefGoogle ScholarPubMed
Dellar, P.J. 2002 Lattice kinetic schemes for magnetohydrodynamics. J. Comput. Phys. 179 (1), 95–126.CrossRefGoogle Scholar
Dellar, P.J. 2009 Moment equations for magnetohydrodynamics. J. Stat. Mech. 2009 (06), P06003.CrossRefGoogle Scholar
Dellar, P.J. 2011 Lattice Boltzmann formulation for Braginskii magnetohydrodynamics. Comput. Fluids 46 (1), 201–205, 10th ICFD Conference Series on Numerical Methods for Fluid Dynamics (ICFD 2010).CrossRefGoogle Scholar
Dellar, P.J. 2013 Lattice Boltzmann magnetohydrodynamics with current-dependent resistivity. J. Comput. Phys. 237, 115–131.CrossRefGoogle Scholar
Dudson, B.D., Allen, A., Breyiannis, G., Brugger, E., Buchanan, J., Easy, L., Farley, S., Joseph, I., Kim, M., McGann, A.D., et al. 2015 Bout: recent and current developments. J. Plasma Phys. 81 (1), 365810104.CrossRefGoogle Scholar
Feraco, F., Marino, R., Pumir, A., Primavera, L., Mininni, P., Pouquet, A. & Rosenberg, D. 2018 Vertical drafts and mixing in stratified turbulence: sharp transition with Froude number. Europhys. Lett. 123, 44002.CrossRefGoogle Scholar
Ferrand, R., Sahraoui, F., Galtier, S., Andrés, N., Mininni, P. & Dmitruk, P. 2022 An in-depth numerical study of exact laws for compressible Hall magnetohydrodynamic turbulence. Astrophys. J. 927 (2), 205.CrossRefGoogle Scholar
Flint, C. & Vahala, G. 2018 A partial entropic lattice Boltzmann MHD simulation of the Orszag–Tang vortex. Radiat. Effects Defects Solids 173 (1–2), 55–65.CrossRefGoogle Scholar
Fox, N.J., Velli, M.C., Bale, S.D., Decker, R., Driesman, A., Howard, R.A., Kasper, J.C., Kinnison, J., Kusterer, M., Lario, D., et al. 2016 The Solar Probe Plus Mission: Humanity's first visit to our star. Space Sci. Rev. 204 (1–4), 7–48.CrossRefGoogle Scholar
Galtier, S. 2016 Introduction to Modern Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Galtier, S. & Buchlin, E. 2007 Multiscale Hall-magnetohydrodynamic turbulence in the solar wind. Astrophys. J. 656 (1), 560–566.CrossRefGoogle Scholar
Geier, M., Greiner, A. & Korvink, J.G. 2006 Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 73, 066705.CrossRefGoogle ScholarPubMed
Geier, M., Greiner, A. & Korvink, J.G. 2007 Properties of the cascaded lattice Boltzmann automaton. Intl J. Mod. Phys. C 18 (04), 455–462.CrossRefGoogle Scholar
Geier, M., Schönherr, M., Pasquali, A. & Krafczyk, M. 2015 The cumulant lattice Boltzmann equation in three dimensions: theory and validation. Comput. Maths Applics. 70 (4), 507–547.CrossRefGoogle Scholar
Gómez, D.O., Mininni, P.D. & Dmitruk, P. 2010 Hall-magnetohydrodynamic small-scale dynamos. Phys. Rev. E 82, 036406.CrossRefGoogle ScholarPubMed
González-Morales, P.A., Khomenko, E. & Cally, P.S. 2019 Fast-to-Alfvén mode conversion mediated by Hall current. II. Application to the solar atmosphere. Astrophys. J. 870 (2), 94.CrossRefGoogle Scholar
He, X. & Luo, L.-S. 1997 Theory of the lattice Boltzmann method: from the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 56, 6811–6817.CrossRefGoogle Scholar
He, X., Shan, X. & Doolen, G.D. 1998 Discrete Boltzmann equation model for nonideal gases. Phys. Rev. E 57, R13–R16.CrossRefGoogle Scholar
Hénon, M. 1987 Viscosity of a lattice gas. Complex Systems 462, 763–789.Google Scholar
Herbert, C., Marino, R., Rosenberg, D. & Pouquet, A. 2016 Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation. J. Fluid Mech. 806, 165–204.CrossRefGoogle Scholar
Higuera, F.J., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9 (4), 345.CrossRefGoogle Scholar
Hoelzl, M., Huijsmans, G.T.A., Pamela, S.J.P., Bécoulet, M., Nardon, E., Artola, F.J., Nkonga, B., Atanasiu, C.V., Bandaru, V., Bhole, A., et al. 2021 The Jorek non-linear extended MHD code and applications to large-scale instabilities and their control in magnetically confined fusion plasmas. Nucl. Fusion 61 (6), 065001.CrossRefGoogle Scholar
Horbury, T.S., O'Brien, H., Carrasco Blazquez, I., Bendyk, M., Brown, P., Hudson, R., Evans, V., Oddy, T.M., Carr, C.M., Beek, T.J., et al. 2020 The Solar Orbiter magnetometer. Astron. Astrophys. 642, A9.CrossRefGoogle Scholar
Horstmann, J., Touil, H., Vienne, L., Ricot, D. & Lévêque, E. 2022 Consistent time-step optimization in the lattice Boltzmann method. J. Comput. Phys. 462, 111224.CrossRefGoogle Scholar
Huba, J.D. 2003 Hall Magnetohydrodynamics - a tutorial. In Space Plasma Simulation (eds. Büchner, J., Dum, C. & Scholer, M.), vol. 615, pp. 166–192. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
d'Humieres, D. 1994 Generalized lattice Boltzmann equations. Prog. Aeronaut. Astronaut. 159, 450–458.Google Scholar
Iroshnikov, P.S. 1963 Turbulence of a conducting fluid in a strong magnetic field. Astron. Zh. 40, 742.Google Scholar
Kiyani, K.H., Osman, K.T. & Chapman, S.C. 2015 Dissipation and heating in solar wind turbulence: from the macro to the micro and back again. Phil. Trans. R. Soc. A 373 (2041), 20140155.CrossRefGoogle Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Körner, C., Pohl, T., Rüde, U., Thürey, N. & Zeiser, T. 2006 Parallel lattice Boltzmann methods for CFD applications. In Numerical Solution of Partial Differential Equations on Parallel Computers (ed. A.M. Bruaset & A. Tveito), pp. 439–466. Springer.CrossRefGoogle Scholar
Kraichnan, R.H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8 (7), 1385–1387.CrossRefGoogle Scholar
Krueger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G. & Viggen, E.M. 2016 The Lattice Boltzmann Method: Principles and Practice. Springer.Google Scholar
Kulsrud, R.M. 2005 Plasma Physics for Astrophysics. Princeton University Press.CrossRefGoogle Scholar
Lewy, H., Friedrichs, K. & Courant, R. 1928 Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 100, 32–74.Google Scholar
Ma, Y., Russell, C.T., Toth, G., Chen, Y., Nagy, A.F., Harada, Y., McFadden, J., Halekas, J.S., Lillis, R., Connerney, J.E.P., et al. 2018 Reconnection in the martian magnetotail: Hall-MHD with embedded Particle-in-Cell simulations. J. Geophys. Res. 123 (5), 3742–3763.CrossRefGoogle Scholar
Mahajan, S.M. & Krishan, V. 2005 Exact solution of the incompressible Hall magnetohydrodynamics. Mon. Not. R. Astron. Soc. 359 (1), L27–L29.CrossRefGoogle Scholar
Malara, F. & Velli, M. 1996 Parametric instability of a large-amplitude nonmonochromatic Alfvén wave. Phys. Plasmas 3 (12), 4427–4433.CrossRefGoogle Scholar
Malaspinas, O. 2015 Increasing stability and accuracy of the lattice Boltzmann scheme: Recursivity and regularization. arXiv:1505.06900.Google Scholar
Marchand, P., Commerçon, B. & Chabrier, G. 2018 Impact of the Hall effect in star formation and the issue of angular momentum conservation. Astron. Astrophys. 619, A37.CrossRefGoogle Scholar
Marino, R., Mininni, P.D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102 (4), 44006.CrossRefGoogle Scholar
Marino, R., Mininni, P.D., Rosenberg, D.L. & Pouquet, A. 2014 Large-scale anisotropy in stably stratified rotating flows. Phys. Rev. E 90, 023018.CrossRefGoogle ScholarPubMed
Marino, R., Pouquet, A. & Rosenberg, D. 2015 a Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114, 114504.CrossRefGoogle ScholarPubMed
Marino, R., Rosenberg, D., Herbert, C. & Pouquet, A. 2015 b Interplay of waves and eddies in rotating stratified turbulence and the link with kinetic-potential energy partition. Europhys. Lett. 112, 49001.CrossRefGoogle Scholar
Marino, R. & Sorriso-Valvo, L. 2023 Scaling laws for the energy transfer in space plasma turbulence. Phys. Rep. 1006, 1–144.CrossRefGoogle Scholar
Marino, R., Sorriso-Valvo, L., Carbone, V., Noullez, A., Bruno, R. & Bavassano, B. 2008 Heating the solar wind by a magnetohydrodynamic turbulent energy cascade. Astrophys. J. Lett. 677 (1), L71.CrossRefGoogle Scholar
Marino, R., Sorriso-Valvo, L., Carbone, V., Veltri, P., Noullez, A. & Bruno, R. 2011 The magnetohydrodynamic turbulent cascade in the ecliptic solar wind: study of Ulysses data. Planet. Space Sci. 59 (7), 592–597.CrossRefGoogle Scholar
Marino, R., Sorriso-Valvo, L., D'Amicis, R., Carbone, V., Bruno, R. & Veltri, P. 2012 On the occurrence of the third-order scaling in high latitude solar wind. Astrophys. J. 750 (1), 41.CrossRefGoogle Scholar
Martínez, D.O., Chen, S. & Matthaeus, W.H. 1994 Lattice Boltzmann magnetohydrodynamics. Phys. Plasmas 1 (6), 1850–1867.CrossRefGoogle Scholar
Matthaeus, W.H., Weygand, J.M., Chuychai, P., Dasso, S., Smith, C.W. & Kivelson, M.G. 2008 Interplanetary magnetic Taylor microscale and implications for plasma dissipation. Astrophys. J. Lett. 678 (2), L141.CrossRefGoogle Scholar
Mendoza, M. & Muñoz, J.D. 2008 Three-dimensional lattice Boltzmann model for magnetic reconnection. Phys. Rev. E 77, 026713.CrossRefGoogle ScholarPubMed
Meyrand, R. & Galtier, S. 2012 Spontaneous chiral symmetry breaking of Hall magnetohydrodynamic turbulence. Phys. Rev. Lett. 109, 194501.CrossRefGoogle ScholarPubMed
Mininni, P.D., Gómez, D.O. & Mahajan, S.M. 2002 Dynamo action in Hall magnetohydrodynamics. Astrophys. J. 567 (1), L81–L83.CrossRefGoogle Scholar
Mininni, P.D., Gomez, D.O. & Mahajan, S.M. 2003 Dynamo action in magnetohydrodynamics and Hall-magnetohydrodynamics. Astrophys. J. 587 (1), 472–481.CrossRefGoogle Scholar
Mininni, P.D., Gomez, D.O. & Mahajan, S.M. 2005 Direct simulations of helical Hall-MHD turbulence and dynamo action. Astrophys. J. 619 (2), 1019–1027.CrossRefGoogle Scholar
Mininni, P.D., Pouquet, A.G. & Montgomery, D.C. 2006 Small-scale structures in three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 97, 244503.CrossRefGoogle ScholarPubMed
Mininni, P.D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI–OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parall. Comput. 37 (6), 316–326.CrossRefGoogle Scholar
Miura, H. & Araki, K. 2014 Structure transitions induced by the Hall term in homogeneous and isotropic magnetohydrodynamic turbulence. Phys. Plasmas 21 (7), 072313.CrossRefGoogle Scholar
Montgomery, D. & Doolen, G.D. 1987 Magnetohydrodynamic cellular automata. Phys. Lett. A 120, 229–231.CrossRefGoogle Scholar
Morales, L., Dasso, S. & Gómez, D. 2005 Hall effect in incompressible magnetic reconnection. J. Geophys. Res. 110, A04204.Google Scholar
Müller, D., St. Cyr, O.C., Zouganelis, I., Gilbert, H.R., Marsden, R., Nieves-Chinchilla, T., Antonucci, E., Auchère, F., Berghmans, D., Horbury, T.S., et al. 2020 The Solar Orbiter mission. Science overview. Astron. Astrophys. 642, A1.CrossRefGoogle Scholar
Norman, C. & Heyvaerts, J. 1985 Anomalous magnetic field diffusion during star formation. Astron. Astrophys. 147 (2), 247–256.Google Scholar
Orszag, S.A. & Tang, C.M. 1979 Small-scale structure of two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 90, 129–143.CrossRefGoogle Scholar
Pandey, B.P. & Wardle, M. 2008 Hall magnetohydrodynamics of partially ionized plasmas. Mon. Not. R. Astron. Soc. 385 (4), 2269–2278.CrossRefGoogle Scholar
Papini, E., Franci, L., Landi, S., Verdini, A., Matteini, L. & Hellinger, P. 2019 Can Hall magnetohydrodynamics explain plasma turbulence at sub-ion scales? Astrophys. J. 870 (1), 52.CrossRefGoogle Scholar
Parashar, T.N., Cuesta, M. & Matthaeus, W.H. 2019 Reynolds number and intermittency in the expanding solar wind: predictions based on Voyager observations. Astrophys. J. Lett. 884 (2), L57.CrossRefGoogle Scholar
Patterson, G.S. & Orszag, S.A. 1971 Spectral calculations of isotropic turbulence: efficient removal of aliasing interactions. Phys. Fluids 14 (11), 2538–2541.CrossRefGoogle Scholar
Pattison, M.J., Premnath, K.N., Morley, N.B. & Abdou, M.A. 2008 Progress in lattice Boltzmann methods for magnetohydrodynamic flows relevant to fusion applications. Fusion Engng Des. 83 (4), 557–572.CrossRefGoogle Scholar
Pouquet, A. & Marino, R. 2013 Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 111, 234501.CrossRefGoogle Scholar
Pouquet, A., Rosenberg, D., Stawarz, J. & Marino, R. 2019 Helicity dynamics, inverse, and bidirectional cascades in fluid and magnetohydrodynamic turbulence: a brief review. Earth Space Sci. 6, 1–19.CrossRefGoogle Scholar
Riley, B., Richard, J. & Girimaji, S.S. 2008 Progress in lattice Boltzmann methods for magnetohydrodynamic schemes in turbulence and rectangular jets. Intl J. Mod. Phys. C 19, 1211–1220.CrossRefGoogle Scholar
Rosenberg, D., Mininni, P.D., Reddy, R. & Pouquet, A. 2020 GPU parallelization of a hybrid pseudospectral geophysical turbulence framework using CUDA. Atmosphere 11, 178.CrossRefGoogle Scholar
Sahraoui, F., Goldstein, M.L., Robert, P. & Khotyaintsev, Y.V. 2009 Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102, 231102.CrossRefGoogle ScholarPubMed
Shan, X. & He, X. 1998 Discretization of the velocity space in the solution of the Boltzmann equation. Phys. Rev. Lett. 80, 65–68.CrossRefGoogle Scholar
Shen, N., Li, Y., Pullin, D.I., Samtaney, R. & Wheatley, V. 2018 On the magnetohydrodynamic limits of the ideal two-fluid plasma equations. Phys. Plasmas 25 (12), 122113.CrossRefGoogle Scholar
Shi, C., Velli, M., Panasenco, O., Tenerani, A., Réville, V., Bale, S.D., Kasper, J., Korreck, K., Bonnell, J.W., Dudok de Wit, T., et al. 2021 Alfvénic versus non-Alfvénic turbulence in the inner heliosphere as observed by Parker Solar Probe. Astron. Astrophys. 650, A21.CrossRefGoogle Scholar
Silva, G. & Semiao, V. 2014 Truncation errors and the rotational invariance of three-dimensional lattice models in the lattice Boltzmann method. J. Comput. Phys. 269, 259–279.CrossRefGoogle Scholar
Smith, C.W., Hamilton, K., Vasquez, B.J. & Leamon, R.J. 2006 Dependence of the dissipation range spectrum of interplanetary magnetic fluctuations on the rate of energy cascade. Astrophys. J. Lett. 645 (1), L85–L88.CrossRefGoogle Scholar
Sorriso-Valvo, L., Marino, R., Foldes, R., Lévêque, E., D´Amicis, R., Bruno, R., Telloni, D. & Yordanova, E. 2023 Helios 2 observations of solar wind turbulence decay in the inner heliosphere. Astron. Astrophys. 672, A13.CrossRefGoogle Scholar
Sovinec, C.R. & King, J.R. 2010 Analysis of a mixed semi-implicit/implicit algorithm for low-frequency two-fluid plasma modeling. J. Comput. Phys. 229 (16), 5803–5819.CrossRefGoogle Scholar
Succi, S., Vergassola, M. & Benzi, R. 1991 Lattice Boltzmann scheme for two-dimensional magnetohydrodynamics. Phys. Rev. A 43, 4521–4524.CrossRefGoogle ScholarPubMed
Telloni, D., Adhikari, L., Zank, G.P., Hadid, L.Z., Sánchez-Cano, B., Sorriso-Valvo, L., Zhao, L., Panasenco, O., Shi, C., Velli, M., et al. 2022 a Observation and modeling of the solar wind turbulence evolution in the sub-Mercury inner heliosphere. Astrophys. J. Lett. 938 (2), L8.CrossRefGoogle Scholar
Telloni, D., Carbone, F., Bruno, R., Zank, G.P., Sorriso-Valvo, L. & Mancuso, S. 2019 Ion cyclotron waves in field-aligned solar wind turbulence. Astrophys. J. Lett. 885 (1), L5.CrossRefGoogle Scholar
Telloni, D., Sorriso-Valvo, L., Woodham, L.D., Panasenco, O., Velli, M., Carbone, F., Zank, G.P., Bruno, R., Perrone, D., Nakanotani, M., et al. 2021 Evolution of solar wind turbulence from 0.1 to 1 au during the first Parker Solar Probe-Solar Orbiter radial alignment. Astrophys. J. Lett. 912 (2), L21.CrossRefGoogle Scholar
Telloni, D., Zank, G.P., Stangalini, M., Downs, C., Liang, H., Nakanotani, M., Andretta, V., Antonucci, E., Sorriso-Valvo, L., Adhikari, L., et al. 2022 Observation of a magnetic switchback in the solar corona. Astrophys. J. Lett. 936 (2), L25.CrossRefGoogle Scholar
Tóth, G., Ma, Y. & Gombosi, T.I. 2008 Hall magnetohydrodynamics on block-adaptive grids. J. Comput. Phys. 227 (14), 6967–6984.CrossRefGoogle Scholar
Wang, X., Bhattacharjee, A. & Ma, Z.W. 2001 Scaling of collisionless forced reconnection. Phys. Rev. Lett. 87, 265003.CrossRefGoogle ScholarPubMed
Xia, Z. & Yang, W. 2015 Exact solutions of the incompressible dissipative Hall magnetohydrodynamics. Phys. Plasmas 22 (3), 032306.CrossRefGoogle Scholar
Yadav, S.K., Miura, H. & Pandit, R. 2022 Statistical properties of three-dimensional Hall magnetohydrodynamics turbulence. Phys. Fluids 34 (9), 095135.CrossRefGoogle Scholar